2.1: Líneas de transmisión

Una línea de transmisión es realmente una cosa larga y continua. Tiene inductancia que es realmente inductancia por unidad de longitud multiplicada por la longitud de línea, pero también tiene una capacitancia continua. Podríamos intentar representar una línea de transmisión larga como una serie de secciones relativamente 'cortas', cada una representada por una inductancia y una capacitancia. Estos modelos de 'parámetros agrupados' para líneas se utilizan realmente en muchos estudios de sistemas, particularmente en modelos analógicos físicos llamados 'Simuladores de Sistemas de Transmisión'. (Construimos uno de estos en el MIT en la década de 1970). Después de la siguiente sección podría contemplar la definición de 'corto' para nuestros propósitos aquí, pero generalmente cada par de capacitancia y resistencia de parámetros agrupados representaría de unas pocas a unas pocas decenas de millas.

Ecuaciones del telégrafo

Al mirar el modelo presentado en la Figura 22, se podría adivinar que una representación adecuada de voltaje y corriente, ambas funciones de tiempo y distancia a lo largo de la línea, podría ser:

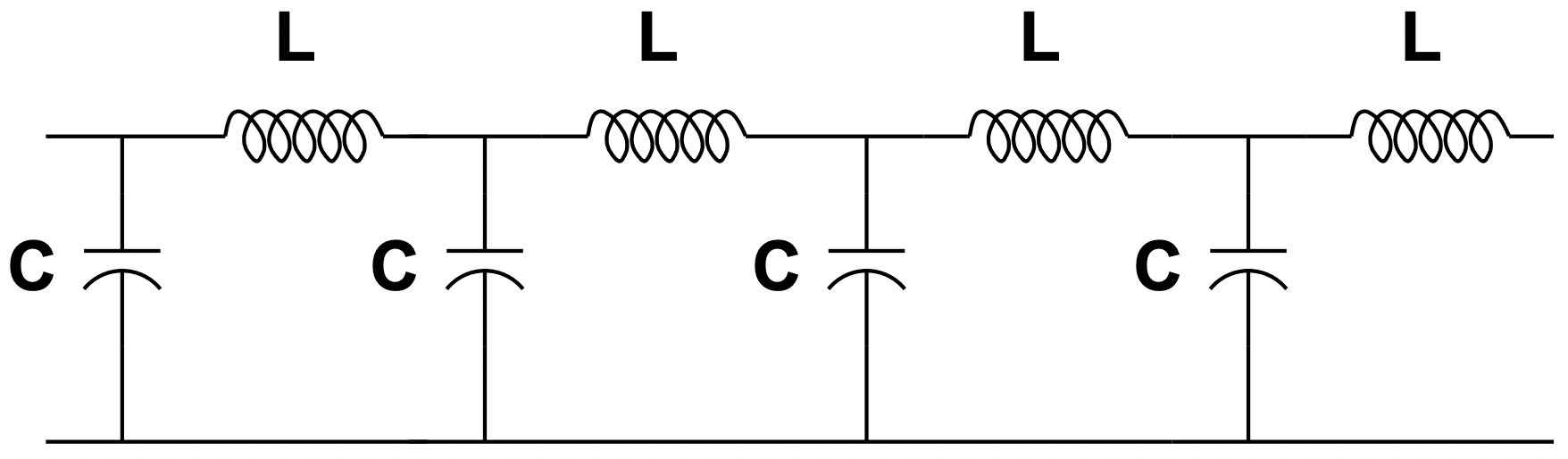Figura 22: Modelo de parámetros agrupados de líneas de transmisión

\ (\\ begin {array} {l}
\ frac {\ v parcial} {\ x parcial} =-L_ {l}\ frac {\ parcial i} {\ parcial t}\
\ frac {\ parcial i} {\ parcial x} =-C_ {l}\ frac {\ v parcial} {\ t parcial}
\ final {array}\)

Estas se conocen como las “Ecuaciones del Telégrafo” y representan el hecho de que la inductancia presenta caída de voltaje a lo largo de la línea en proporción a la tasa de cambio de corriente y que la capacitancia presenta un cambio en la corriente a lo largo de la línea en proporción a la tasa de cambio de voltaje.

No es difícil eliminar ya sea voltaje o corriente de estos para producir una ecuación de onda. Por ejemplo, tome las derivadas cruzadas y sustituya la segunda de estas ecuaciones por la primera para obtener:

\(\ \frac{\partial^{2} v}{\partial x^{2}}=L_{l} C_{l} \frac{\partial^{2} v}{\partial t^{2}}\)

Ahora: esta ecuación se resuelve mediante funciones arbitrarias que son de la forma:

\(\ v(x, t)=v(x \pm u t)\)

donde la velocidad de onda es:

\(\ u=\frac{1}{\sqrt{L_{l} C_{l}}}\)

Entonces ahora podemos ver que el voltaje en la línea es la suma de alguna forma de onda que va en la dirección 'positiva' y algo más va en la dirección 'negativa':

\(\ v(x, t)=v_{+}(x-u t)+v_{-}(x+u t)\)

Lo mismo será cierto de la corriente, y sustituir de nuevo en cualquiera de las ecuaciones del telégrafo arroja:

\(\ i(x, t)=\frac{1}{L_{l} u}\left(v_{+}(x-u t)-v_{-}(x+u t)\right)\)

el producto de la inductancia veces la velocidad de onda tiene las unidades de impedancia:

\(\ L_{l} u=\sqrt{\frac{L_{l}}{C_{l}}}=Z_{0}\)

Esto a menudo se conoce como la 'impedancia caracterítica' de la línea de transmisión. Este es también un término de uso común: los cables de transmisión a menudo se refieren por sus impedancias características. Para cables coaxiales de 50 a 72 ohmios son valores comunes. Para líneas de transmisión de alta tensión se esperan valores algo más altos.

Sobretensiones en líneas de transmisión

Considera la situación que se muestra en la Figura 23. Aquí el extremo izquierdo de la línea es accionado por una fuente de corriente con un pulso (ilustrado es un pulso cuadrado). Esto en realidad no está muy lejos de la situación que experimentan las líneas de transmisión con los rayos, que generalmente es representable como una fuente de corriente, típicamente de magnitud entre 20 y 100 kA y duración de aproximadamente 1µS. (En realidad, no es un pulso cuadrado pero eso no es importante aquí).

Lo que va a pasar, si el pulso es lo suficientemente corto, es que lanzará una onda viajera en la que\(\ v_{+}=Z_{0} i_{+}\) y\(\ i_{+}\) es la corriente que se impuso. Cuando este pulso llega al extremo lejano, o carga de la línea, tenemos la situación en la que en ese punto:

\ (\\ comenzar {alineado}
v (t) &=v_ {+} +v_ {-}\\
i (t) &=\ frac {v_ {+}} {Z_ {0}} -\ frac {V_ {-}} {Z_ {0}}
\ end {alineado}\)

y, de coures,\(\ v=R i\).

La onda 'reflejada', o negativa va a tener magnitud:

\(\ v_{-}=v_{+} \frac{\frac{R}{Z_{0}}-1}{\frac{R}{Z_{0}}+1}\)

En el caso extremo de un circuito abierto, la magnitud del pulso de voltaje al final de la línea de transmisión es exactamente el doble que la del pulso de propagación. En el caso de un cortocircuito, por supuesto, la magnitud de la tensión es cero, la corriente en el corto es el doble de la corriente del pulso en sí, y el pulso se refleja, pero yendo en sentido inverso con una polaridad opuesta al pulso de avance. Esto se ilustra en forma de dibujos animados en la Figura 23.

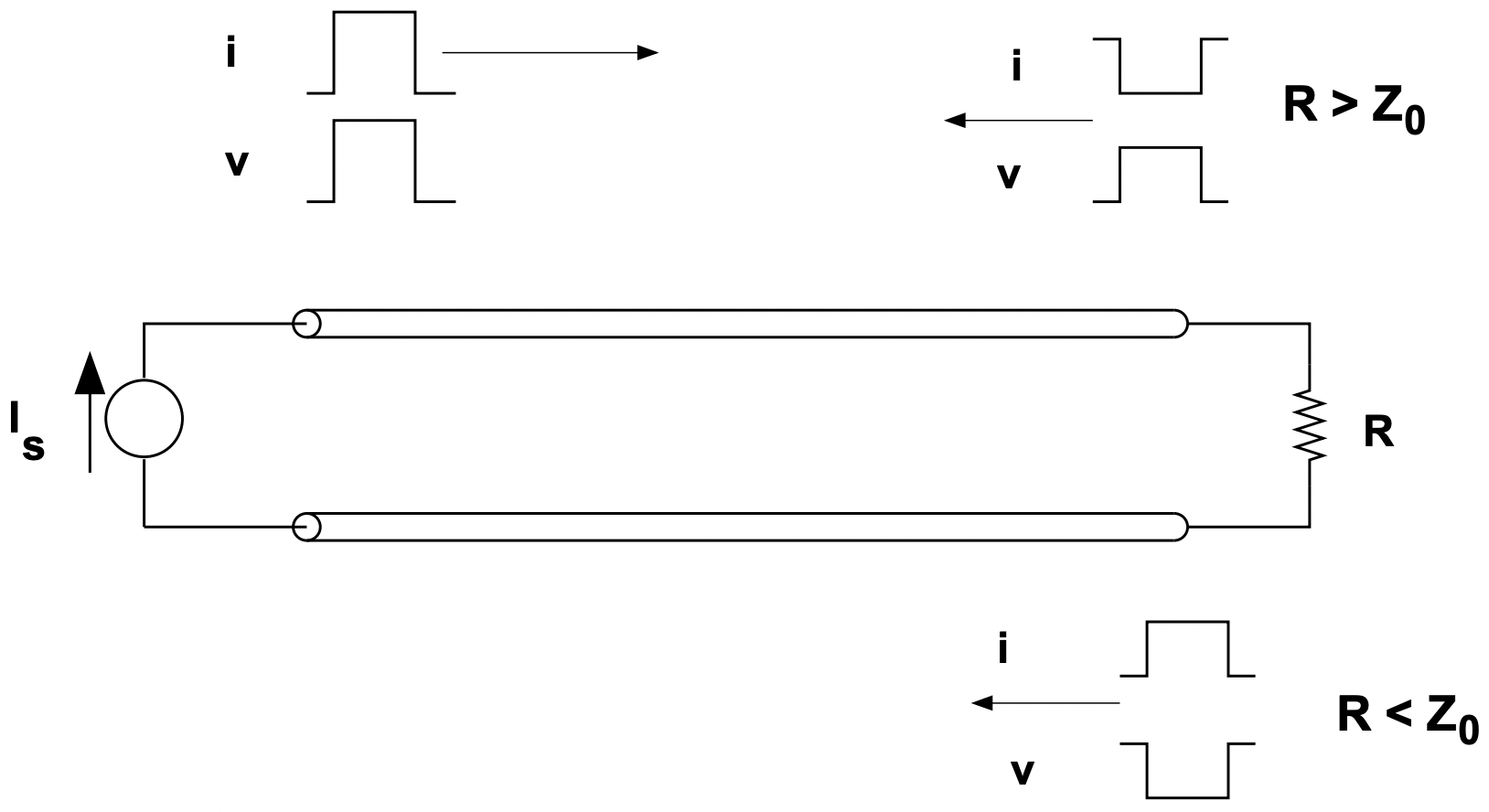Figura 23: Propagación de impulsos en una línea de transmisión

Estado estacionario sinusoidal

Ahora, considere una línea de transmisión operando en el estado estacionario sinusoidal. Como sugiere la Figura 24, es accionado por una fuente de voltaje en un extremo y es cargado por una carga resistiva en el otro. Consistente con el voltaje y las corrientes que sabemos que pueden existir en tal línea, sabemos que serán de esta forma:

Figura 24: Línea de transmisión en configuración simple

\ (\\ comenzar {alineado}
v (x, t) &=\ nombreoperador {Re}\ izquierda\ {\ subrayado {V} _ {+} e^ {j (\ omega t-k x)} +\ subrayado {V} _ {-} e^ {j (\ omega t+k x)}\ derecha\}\\
i (x, t) &=\ nombreoperador {Re}\ izquierda\ {\ frac {V_ {+}} {Z_ {0}} e^ {j (\ omega t-k x)} -\ frac {V} {Z_ {0}} e^ {j (\ omega t+k x)}\ derecha\}
\ fin {alineado}\)

Dónde está la velocidad de fase\(\ u=\frac{\omega}{k}=\frac{1}{\sqrt{L_{l} C_{l}}}\).

Al final de terminación de la línea, en\(\ x=\ell\)

\ (\\ comenzar {ecuación}
R=\ frac {\ subrayado {V}} {\ subrayado {I}} =Z_ {0}\ frac {\ subrayado {V} _ {+} e^ {-j k\ ell} +\ subrayado {V} _ _ {-} e^ {j k\ ell}} {\ subrayado {V} _ _ {+} e^ {-j k\ ell} -\ subrayado {V} _ {-} e^ {j k\ ell}}
\ final {ecuación}\)

Esto se puede resolver para la relación de amplitud 'inversa' a 'directa':

\ (\\ comenzar {ecuación}
\ subrayado {V} _ {-} =\ subrayado {V} _ _ {+} e^ {-2 j k\ ell}\ frac {\ frac {R} {Z_ {0}} -1} {\ frac {R} {Z_ {0}} +1}
\ final {ecuación}\)

Ya que al final del 'envío':

\ (\\ comenzar {ecuación}
V_ {s} =\ subrayado {V} _ {+} +\ subrayado {V} _ _ {-}
\ final {ecuación}\)

Con un poco de manipulación se puede determinar que

\(\ \underline{V}_{r}=V_{s} \frac{e^{-j k \ell}\left[\left(\frac{R}{Z_{0}}+1\right)+\left(\frac{R}{Z_{0}}-1\right)\right]}{\left(\frac{R}{Z_{0}}+1\right)+e^{-2 j k \ell}\left(\frac{R}{Z_{0}}-1\right)}\)

La manipulación adicional rinde:

\(\ \underline{V}_{r}=V_{s} \frac{\frac{R}{Z_{0}}}{\frac{R}{Z_{0}} \cos k \ell+j \sin k \ell}\)

Esto podría hacerse un poco más comprensible cuando se convierte en una magnitud:

\(\ \left|\frac{V_{r}}{V_{s}}\right|=\frac{\frac{R}{Z_{0}}}{\sqrt{\left(\frac{R}{Z_{0}} \cos k \ell\right)^{2}+(\sin k \ell)^{2}}}\)

Si la línea está cargada con una resistencia equivalente a la 'impedancia de sobretensión' (la llamada 'carga de impedancia de sobretensión', la tensión final de recepción es la misma que la tensión final de envío. Si está más cargado, el voltaje del extremo receptor es menor que el extremo de envío y si está menos cargado, el voltaje del extremo receptor es mayor.