2.2: Notación Exponencial Compleja

Comienza reconociendo una interpretación geométrica para un número complejo. Si trazamos la parte real en el eje horizontal (x) y la parte imaginaria en el eje vertical (y), entonces el número complejo\(\ \underline{z}=x+j y\) (donde\(\ j=\sqrt{-1}\)) representa un vector como se muestra en la Figura 1. Tenga en cuenta que este vector puede estar representado no solo por sus componentes reales e imaginarios, sino también por una magnitud y un ángulo de fase:

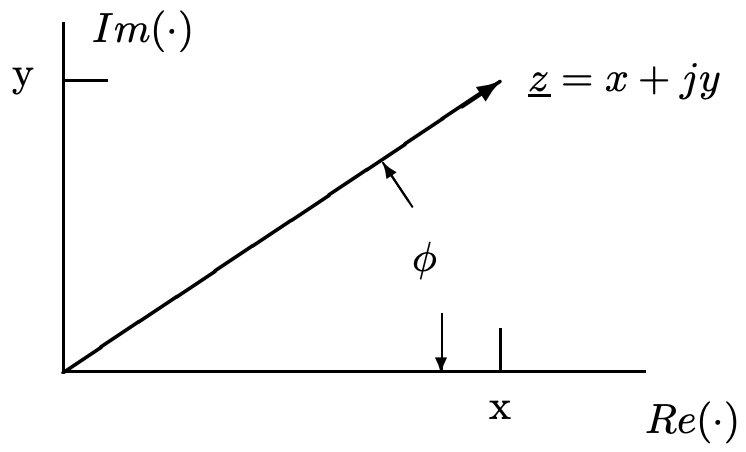Figura 1: Representación del número complejo\(\ \underline{z}=x+j y\)

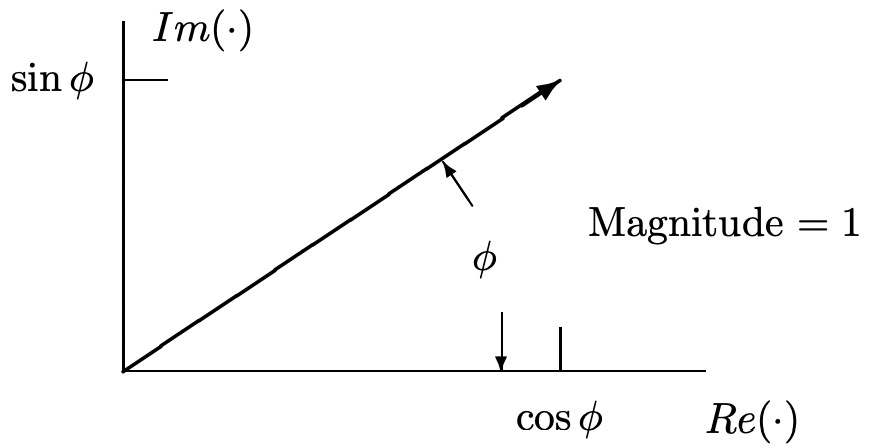Figura 2: Representación de\(\ e^{j \phi}\)

\[\ |\underline{z}|=\sqrt{x^{2}+y^{2}}\label{1} \]

\[\ \phi=\arctan \left(\frac{y}{x}\right)\label{2} \]

La base de la notación exponencial compleja es la célebre Relación de Euler:

\[\ e^{j \phi}=\cos (\phi)+j \sin (\phi)\label{3} \]

que tiene una representación como se muestra en la Figura 2.

Ahora bien, una comparación de las figuras 1 y 2 deja claro que, con las definiciones (1) y (2),

\[\ \underline{z}=x+j y=|\underline{z}| e^{j \phi}\label{4} \]

Es sencillo, usar (3) para mostrar que:

\[\ \cos (\phi)=\frac{e^{j \phi}+e^{-j \phi}}{2}\label{5} \]

\[\ \sin (\phi)=\frac{e^{j \phi}-e^{-j \phi}}{2 j}\label{6} \]

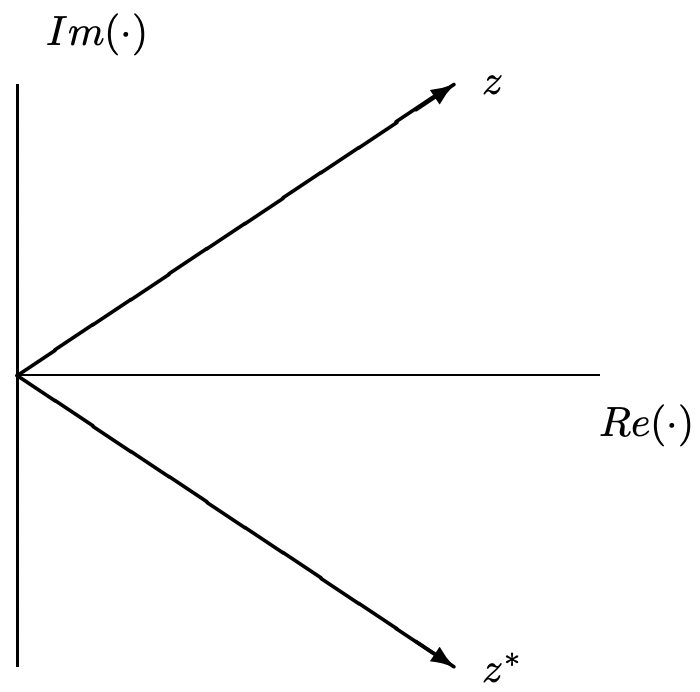Figura 3: Representación de un número complejo y su conjugado

El exponencial complejo es un tipo de función tremendamente útil. Obsérvese que el producto de dos números expresados como exponenciales es el mismo que el exponencial de las sumas de los dos exponentes:

\[\ e^{a} e^{b}=e^{a+b}\label{8} \]

Tenga en cuenta que también es cierto que el recíproco de un número en notación exponencial es solo el exponencial de lo negativo del exponente:

\[\ \frac{1}{e^{a}}=e^{-a}\label{9} \]

Entonces, si tenemos dos números\(\ \underline{z}_{1}=\left|\underline{z}_{1}\right| e^{j \phi_{1}}\) y\(\ \underline{z}_{2}=\left|\underline{z}_{2}\right| e^{j \phi_{2}}\), entonces el producto de los dos números es:

\[\ \underline{z}_{1} \underline{z}_{2}=\left|\underline{z}_{1} \| \underline{z}_{2}\right| e^{j\left(\phi_{1}+\phi_{2}\right)}\label{10} \]

y la relación de los dos números es:

\[\ \frac{\underline{z}_{1}}{\underline{z}_{2}}=\frac{\left|\underline{z}_{1}\right|}{\left|\underline{z}_{2}\right|} e^{j\left(\phi_{1}-\phi_{2}\right)}\label{11} \]

El complejo conjugado de un número\(\ \underline{z}=x+j y\) viene dado por:

\[\ z^{*}=x-j y\label{12} \]

La suma de un número complejo y su conjugado es real:

\[\ \underline{z}+\underline{z}^{*}=2 \operatorname{Re}(\underline{z})=2 x\label{13} \]

mientras que la diferencia es imaginaria:

\[\ \underline{z}-\underline{z}^{*}=2 j \operatorname{Im}(\underline{z})=2 j y\label{14} \]

donde hemos utilizado los dos símbolos\(\ {Re}(\cdot)\) y\(\ {Im}(\cdot)\) para representar a los operadores que extraen las partes real e imaginaria del número complejo.

El conjugado complejo de un número complejo también\(\ \underline{z}=|\underline{z}| e^{j \phi}\) puede escribirse como:

\[\ \underline{z}^{*}=|\underline{z}| e^{-j \phi}\label{15} \]

para que el producto de un número complejo y su conjugado sea real:

\[\ \underline{z z}^{*}=|\underline{z}| e^{j \phi}|\underline{z}| e^{-j \phi}=|\underline{z}|^{2}\label{16} \]