6.3: Ley de Faraday e Inductancia

Los campos magnéticos cambiantes dan lugar a campos eléctricos y, en consecuencia, producen voltaje. Así es como funciona la inductancia. Consideremos la situación que se muestra de manera bastante abstracta en la Figura 5.

La Ley de Faraday es, en forma integral:

\(\ \oint \vec{E} \cdot d \ell=-\frac{d}{d t} \iint \ _\text { Area } \vec{B} \cdot \vec{n} d a\)

Si el contorno mostrado es altamente conductor (digamos, si es un cable), hay cero campo eléctrico sobre esa parte del contorno. El voltaje a través de los terminales es:

\(\ V_{a b}=\int_{a}^{b} \vec{E} \cdot d \ell\)

y esa es la totalidad de la integral anterior. Así podemos concluir que:

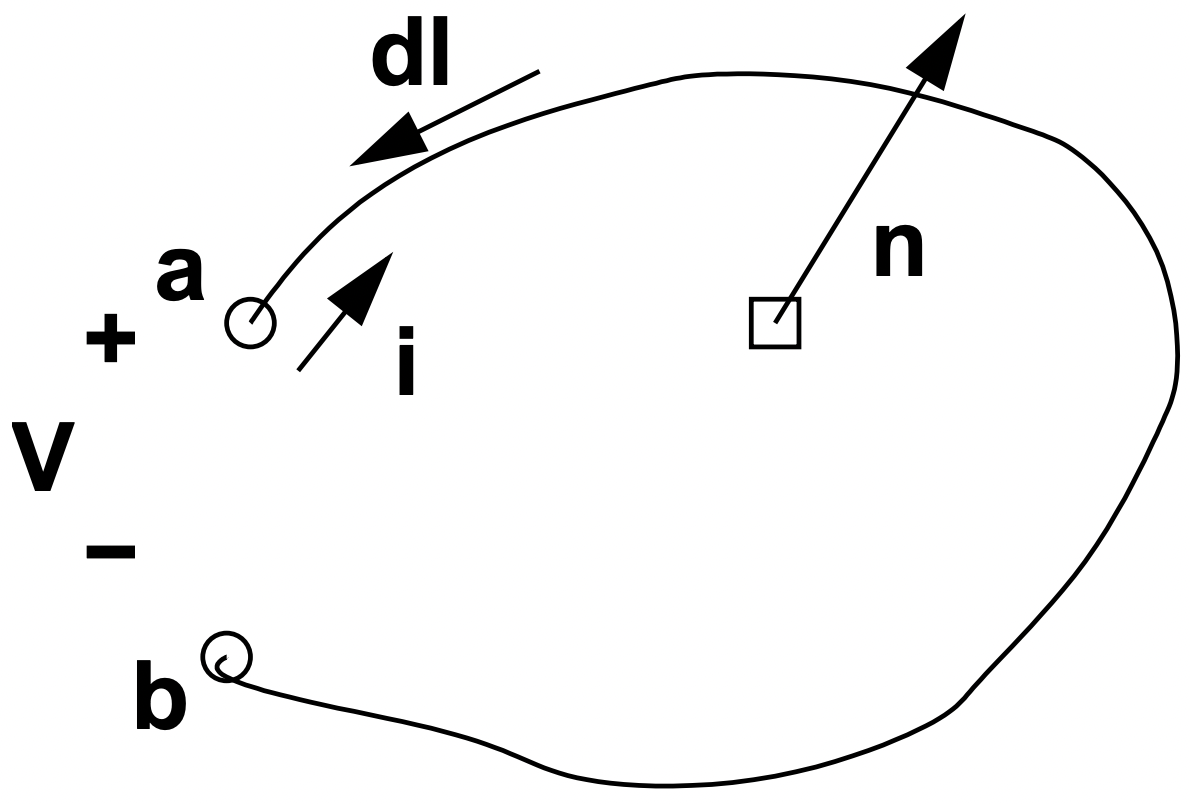Figura 5: Bucle para la Ley de Faraday

\(\ V_{a b}=-\frac{d}{d t} \iint \ _\text { Area } \vec{B} \cdot \vec{n} d a\)

Ahora bien, si definimos el flujo vinculado por este contorno para que sea:

\(\ \lambda=-\iint \ _\text{Area} \vec{B} \cdot \vec{n} d a\)

entonces el voltaje es, como esperamos:

\(\ V_{a b}=\frac{d \lambda}{d t}\)

Resulta que la corriente que fluye en el cable con sentido mostrado por i en la Figura 5 tiende a producir flujo con sentido opuesto al vector normal mostrado en esa figura, y así produce flujo positivo. Generalmente, al calcular la inductancia, se utiliza la 'regla de la mano derecha' para determinar la dirección del enlace del flujo: si los dedos de tu mano derecha siguen la dirección del devanado, desde el terminal positivo, el flujo positivo está en la dirección de tu pulgar.

Ejemplo: Actuador Solenoide

En la Figura 6 se muestra una representación de un actuador de solenoide común. Cuando se pone corriente a través de la bobina aparece un flujo magnético en los huecos y tira del émbolo hacia la izquierda. Examinaremos la fuerza y cómo calcularla en capítulos posteriores. Por ahora, sin embargo, nos preocupan los campos magnéticos en el dispositivo y con el cálculo de la inductancia. Supongamos que el estator y el émbolo están hechos de materiales altamente permeables\(\ (\mu \rightarrow \infty)\). Si la bobina transporta corriente\(\ I\) en\(\ N\) giros en el sentido mostrado, el flujo magnético cruzará el entrehierro estrecho hacia la derecha en la dirección del estator al émbolo y luego regresará en el sentido mostrado en el espacio de longitud variable de ancho\(\ x\). Está claro que esto también es flujo de sentido positivo para la bobina.

El equivalente del circuito magnético se muestra en la Figura 7. Todo el flujo producido cruza el hueco de ancho variable que tiene reluctancia:

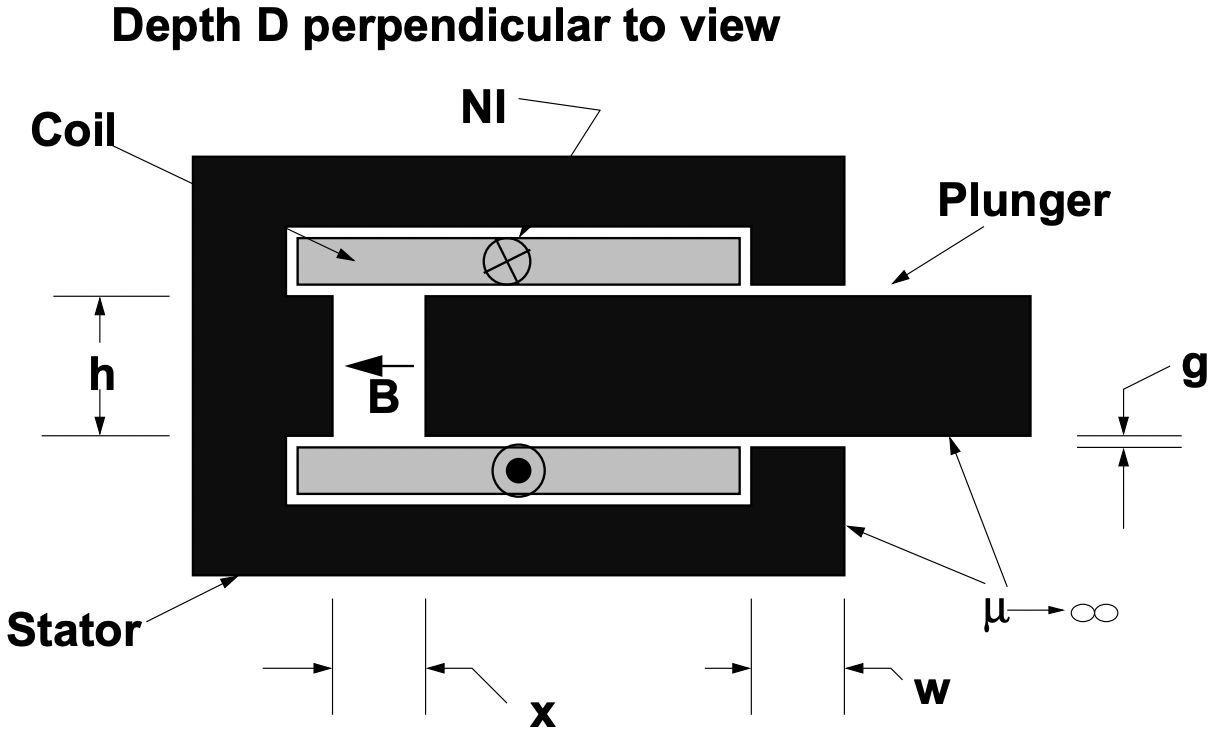Figura 6: Sección transversal del actuador de solenoide

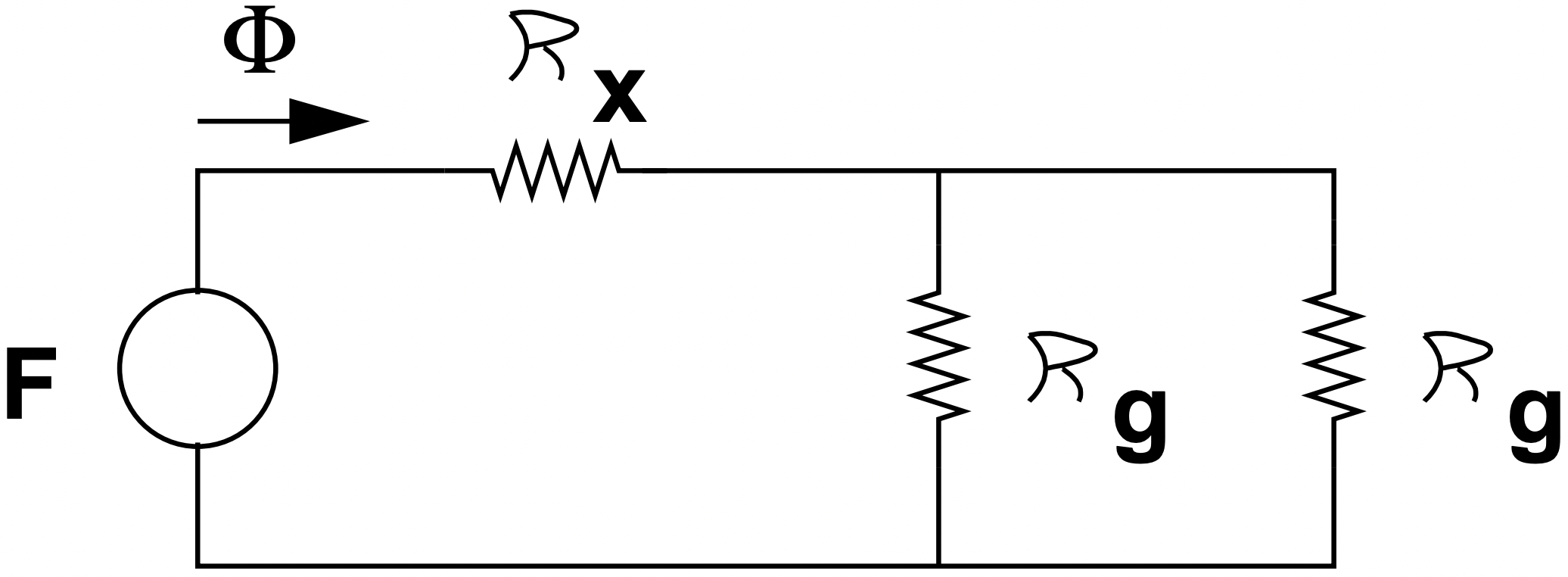Figura 7: Circuito Magnético Equivalente del Actuador Solenoide

\(\ \mathcal{R}_{x}=\frac{x}{\mu_{0} h D}\)

La mitad del flujo cruza cada uno de los otros dos huecos, que están en paralelo y tienen reluctancia:

\(\ \mathcal{R}_{g}=\frac{g}{\mu_{0} w D}\)

El flujo total en el circuito magnético es

\(\ \Phi=\frac{F}{\mathcal{R}_{x}+\frac{1}{2} \mathcal{R}_{g}}\)

Y desde\(\ \lambda=N \Phi\) y\(\ F=N I\), la inductancia de esta estructura es:

\(\ L=\frac{N^{2}}{\mathcal{R}}=\frac{N^{2}}{\mathcal{R}_{x}+\frac{1}{2} \mathcal{R}_{g}}\)