8.1: Proceso de Conversión de Energía

En un motor el proceso de conversión de energía puede pensarse en términos simples. En “estado estacionario”, la entrada de energía eléctrica a la máquina es solo la suma de las entradas de energía eléctrica a los diferentes terminales de fase:

\(\ P_{e}=\sum_{i} v_{i} i_{i}\)

La potencia mecánica es par veces velocidad:

\(\ P_{m}=T \Omega\)

Y la suma de las pérdidas es la diferencia:

\(\ P_{d}=P_{e}-P_{m}\)

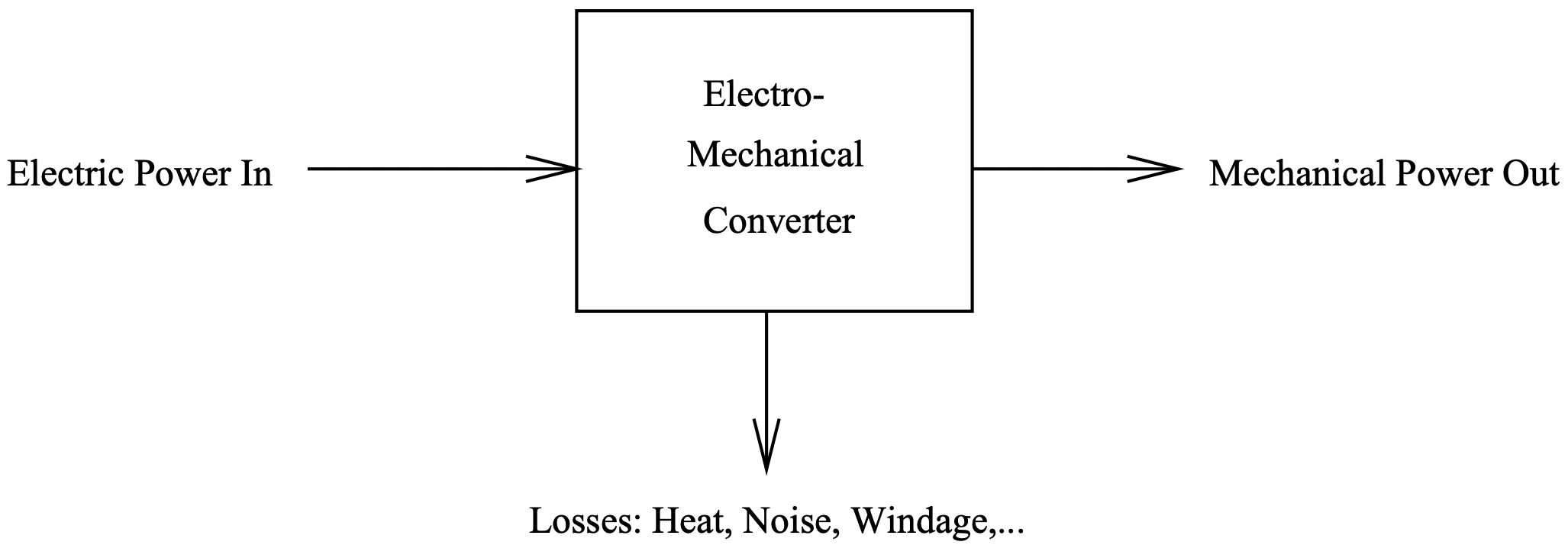Figura 1: Proceso de conversión de energía

A veces será conveniente emplear el hecho de que, en la mayoría de las máquinas, la disipación es lo suficientemente pequeña como para aproximarse a la potencia mecánica con la energía eléctrica. De hecho, son muchas las situaciones en las que el mecanismo de pérdida se conoce lo suficientemente bien como para que pueda ser idealizado de distancia. Los argumentos “termodinámicos” para la densidad de fuerza aprovechan esto y emplean un sistema de conversión de energía “conservador” o sin pérdidas.

Enfoque Energético a las Fuerzas Electromagnéticas:

Figura 2: Sistema Conservador de Campo Magnético

Para comenzar, considere algún sistema electromecánico que tenga dos juegos de “terminales”, eléctricos y mecánicos, como se muestra en la Figura 2. Si el sistema almacena energía en campos magnéticos, la energía almacenada depende del estado del sistema, definida por (en este caso) por dos de las variables identificables: flujo\(\ (\lambda)\), corriente\(\ (i)\) y posición mecánica\(\ (x)\). De hecho, con solo un poco de reflexión, deberías poder convencerte de que este estado es una función de valor único de dos variables y que la energía almacenada es independiente de cómo se llevó el sistema a este estado.

Ahora, todos los convertidores electromecánicos tienen mecanismos de pérdida y por lo tanto no son conservadores en sí mismos. Sin embargo, el sistema de campo magnético que produce fuerza es, en principio, conservador en el sentido de que su estado y energía almacenada pueden ser descritos por sólo dos variables. La “historia” del sistema no es importante.

Es posible elegir las variables de tal manera que la energía eléctrica en este sistema conservador sea:

\(\ P^{e}=v i=i \frac{d \lambda}{d t}\)

Del mismo modo, la salida mecánica del sistema es:

\(\ P^{m}=f^{e} \frac{d x}{d t}\)

La diferencia entre estos dos es la tasa de cambio de la energía almacenada en el sistema:

\(\ \frac{d W_{m}}{d t}=P^{e}-P^{m}\)

Entonces es posible calcular el cambio de energía requerido para llevar el sistema de un estado a otro mediante:

\(\ W_{m}(a)-W_{m}(b)=\int_{b}^{a} i d \lambda-f^{e} d x\)

donde los dos estados del sistema son descritos por\(\ a=\left(\lambda_{a}, x_{a}\right)\) y\(\ b=\left(\lambda_{b}, x_{b}\right)\)

Si la energía almacenada en el sistema es descrita por dos variables de estado,\(\ \lambda\) y\(\ x\), el diferencial total de la energía almacenada es:

\(\ d W_{m}=\frac{\partial W_{m}}{\partial \lambda} d \lambda+\frac{\partial W_{m}}{\partial x} d x\)

y también es:

\(\ d W_{m}=i d \lambda-f^{e} d x\)

Para que podamos hacer una equivalencia directa entre los derivados y:

\(\ f^{e}=-\frac{\partial W_{m}}{\partial x}\)

Esto generaliza en el caso de múltiples terminales eléctricos y/o múltiples terminales mecánicos. Por ejemplo, una situación con múltiples terminales eléctricos tendrá:

\(\ d W_{m}=\sum_{k} i_{k} d \lambda_{k}-f^{e} d x\)

Y el caso del movimiento rotativo, a diferencia del lineal, tiene en lugar de fuerza\(\ f^{e}\) y desplazamiento\(\ x\), torque\(\ T^{e}\) y desplazamiento angular\(\ \theta\).

En muchos casos podríamos considerar un sistema que es electricamente lineal, en cuyo caso la inductancia es una función únicamente de la posición mecánica\(\ x\).

\(\ \lambda(x)=L(x) i\)

En este caso, suponiendo que la integral energética se lleve a cabo desde\(\ \lambda=0\) (para que la parte de la integral realizada sobre\(\ x\) sea cero),

\(\ W_{m}=\int_{0}^{\lambda} \frac{1}{L(x)} \lambda d \lambda=\frac{1}{2} \frac{\lambda^{2}}{L(x)}\)

Esto hace

\(\ f^{e}=-\frac{1}{2} \lambda^{2} \frac{\partial}{\partial x} \frac{1}{L(x)}\)

Tenga en cuenta que esto es numéricamente equivalente a

\(\ f^{e}=-\frac{1}{2} i^{2} \frac{\partial}{\partial x} L(x)\)

Esto es cierto sólo en el caso de un sistema lineal. Tenga en cuenta que sustituir\(\ L(x) i=\lambda\) demasiado pronto en la derivación produce resultados erróneos: en el caso de un sistema lineal es un error de signo, pero en el caso de un sistema no lineal es simplemente incorrecto.

Coenergía

A menudo describiremos los sistemas en términos de inductancia en lugar de su recíproco, de manera que la corriente, más que el flujo, parece ser la variable relevante. Es conveniente derivar una nueva variable energética, a la que llamaremos coenergía, mediante:

\(\ W_{m}^{\prime}=\sum_{i} \lambda_{i} i_{i}-W_{m}\)

y en este caso es bastante fácil demostrar que el diferencial de energía es (para una sola variable mecánica) simplemente:

\(\ d W_{m}^{\prime}=\sum_{k} \lambda_{k} d i_{k}+f^{e} d x\)

para que la fuerza producida sea:

\(\ f_{e}=\frac{\partial W_{m}^{\prime}}{\partial x}\)

Considera un ejemplo simple de máquina eléctrica en el que hay un solo devanado en un rotor (llámalo el devanado de campo y una armadura polifásica. Supongamos que el rotor es redondo para que podamos describir los enlaces de flujo como:

\ (\\ begin {array} {l}
\ lambda_ {a} =L_ {a} i_ {a} +L_ {a b} i_ {b} +L_ {a b} i_ {c} +M\ cos (p\ theta) i_ {f}\\
\ lambda_ {b} =L_ {a b} i_ {a} i_ {a} +l_ {a} +l_ {a}} i_ {b} +L_ {a b} i_ {c} +M\ cos\ izquierda (p\ theta-\ frac {2\ pi} {3}\ derecha) i_ {f}\
\ lambda_ {c} =L_ {a b} i_ {a} +L_ {a b} i_ {a b} i_ {b} +L_ {a} i_ {c} +L_ {a} M\ cos\ izquierda (p\ theta+\ frac {2\ pi} {3}\ derecha) i_ {f}\
\ lambda_ {f} =M\ cos (p\ theta) i_ {a} +M\ cos\ izquierda (p\ theta-\ frac {2\ pi} {3}\ derecha) i_ {b} +M\ cos\ izquierda (p\ theta+\ frac {2\ pi} {3}\ derecha) +L_ {f} i_ {f}
\ end {array}\)

Ahora bien, este sistema puede describirse simplemente en términos de coenergía. Con excitación múltiple es importante tener cierto cuidado al tomar la coenergía integral (para asegurar que se tome sobre un camino válido en el espacio multidimensional). En nuestro caso en realidad hay cinco dimensiones, pero solo cuatro son importantes ya que podemos posicionar el rotor con todas las corrientes a cero por lo que no hay contribución a la coenergía desde el ajuste de la posición del rotor. Supongamos que el rotor está en algún ángulo\(\ \theta\) y que las cuatro corrientes tienen valores\(\ i_{a 0}\),\(\ i_{b 0}\),\(\ i_{c 0}\) y\(\ i_{f 0}\). Una de las muchas integrales de ruta correctas a tomar sería:

\ (\\ begin {array} {l}
W_ {m} ^ {\ prime} &=\ int_ {0} ^ {i_ {a 0}} L_ {a} i_ {a} d i_ {a}\\
&+\ int_ {0} ^ {i_ {b 0}}\ left (L_ {a b} i_ {a 0} +L_ {a} i_ {b}\ derecha) d i_ {b}\\
&+\ int_ {0} ^ {i_ {c 0}}\ izquierda (L_ {a b} i_ {a 0} +L_ {a b} i_ {b 0} +L_ {a} i_ {c}\ derecha) d i_ {c}\\
& amp; +\ int_ {0} ^ {i_ {f 0}}\ izquierda (M\ cos (p\ theta) i_ {a 0} +M\ cos\ izquierda (p\ theta-\ frac {2\ pi} {3}\ derecha) i_ {b 0} +M\ cos\ izquierda (p\ theta+\ frac {2\ pi} {3}\ derecha) i_ {c 0} +L_ {f} i_ {f}\ derecha) d i_ {f}
\ end {array}\)

El resultado es:

\ (\\ begin {alineado}
W_ {m} ^ {\ prime} &=\ frac {1} {2} L_ {a}\ izquierda (i_ {a 0} ^ {2} +i_ {b 0} ^ {2} +i_ {c o} ^ {2}\ derecha) +L_ {a b}\ izquierda (i_ {a o} i_ {b} +i_ {a o} i_ {c 0} +i_ {c o} i_ {b 0}\ derecha)\\
&+M i_ {f 0}\ izquierda (i_ {a 0}\ cos (p\ theta) +i_ {b 0}\ cos\ izquierda (p\ theta-\ frac {2\ pi} {3}\ derecha) +i_ {c 0}\ cos\ izquierda (p\ theta+\ frac {2\ pi} {3}\ derecha)\ derecha) +\ frac {1} {2} L_ {f} i_ {f 0} ^ {2}
\ end {alineado}\)

Si no hay variación de las inductancias del estator con la posición del rotor\(\ \theta\), (que sería el caso si el rotor fuera perfectamente redondo), los términos que implican\(\ L_{a}\) y\(\ \left.L_{(} a b\right)\) aportan cero para que el par esté dado por:

\(\ T_{e}=\frac{\partial W_{m}^{\prime}}{\partial \theta}=-p M i_{f 0}\left(i_{a 0} \sin (p \theta)+i_{b 0} \sin \left(p \theta-\frac{2 \pi}{3}\right)+i_{c o} \sin \left(p \theta+\frac{2 \pi}{3}\right)\right)\)

Volveremos a este tipo de máquinas en capítulos posteriores.

Flujo continuo de energía

En este punto, es instructivo pensar en el flujo de energía electromagnética como lo describe el Teorema de Poynting:

\(\ \vec{S}=\vec{E} \times \vec{H}\)

El flujo de energía\(\ \vec{S}\), llamado Vector de Poynting, describe la potencia electromagnética en términos de campos eléctricos y magnéticos. Es densidad de potencia: potencia por unidad de área, con unidades en el sistema SI de unidades de vatios por metro cuadrado.

Para calcular la potencia electromagnética en algún volumen de espacio, podemos integrar el Vector de Poyting sobre la superficie de ese volumen, y luego usar el teorema de divergencia:

\(\ P=-\oiint \vec{S} \cdot \vec{n} d a=-\int_{\mathrm{VOl}} \nabla \cdot \vec{S} d v\)

Ahora, la divergencia del Vector Poynting es, usando una identidad vectorial:

\ (\\ comenzar {alineado}
\ nabla\ cdot\ vec {S} &=\ nabla\ cdot (\ vec {E}\ veces\ vec {H}) =\ vec {H}\ cdot\ nabla\ veces\ vec {E} -\ vec {E}\ cdot\ nabla\ veces\ vec {H}\\
&=-\ vec {H}\ cdot\ frac {\ parcial\ vec {B}} {\ parcial t} -\ vec {E}\ cdot\ vec {J}
\ final {alineado}\)

El poder que cruza hacia una región del espacio es entonces:

\(\ P=\int_{\mathrm{vol}}\left(\vec{E} \cdot \vec{J}+\vec{H} \cdot \frac{\partial \vec{B}}{\partial t}\right) d v\)

Ahora bien, a falta de movimiento material, la interpretación de los dos términos en esta ecuación es bastante simple. El primer término describe la disipación:

\(\ \vec{E} \cdot \vec{J}=|\vec{E}|^{2} \sigma=|\vec{J}|^{2} \rho\)

El segundo término se interpreta como tasa de cambio de la energía magnética almacenada. En ausencia de histéresis es:

\(\ \frac{\partial W_{m}}{\partial t}=\vec{H} \cdot \frac{\partial \vec{B}}{\partial t}\)

Obsérvese que en el caso del espacio libre,

\(\ \vec{H} \cdot \frac{\partial \vec{B}}{\partial t}=\mu_{0} \vec{H} \cdot \frac{\partial \vec{H}}{\partial t}=\frac{\partial}{\partial t}\left(\frac{1}{2} \mu_{0}|\vec{H}|^{2}\right)\)

que se interpreta directamente como la tasa de cambio de la densidad de energía magnética almacenada:

\(\ W_{m}=\frac{1}{2} \mu_{0}|H|^{2}\)

Algunos materiales presentan un comportamiento histerético, en el que la energía almacenada no es una sola función valorada de ninguno\(\ \vec{B}\) o\(\ \vec{H}\), y consideraremos ese caso anon.

Movimiento de Material

En presencia de movimiento material\(\ \vec{v}\), el campo eléctrico\(\ \overrightarrow{E^{\prime}}\) en un marco “móvil” se relaciona con el campo eléctrico\(\ \vec{E}\) en un marco “estacionario” y con el campo magnético\(\ \vec{B}\) por:

\(\ \vec{E}^{\prime}=\vec{E}+\vec{v} \times \vec{B}\)

Este es un resultado experimental obtenido al observar partículas cargadas que se mueven en campos eléctricos y magnéticos combinados. Se trata de una expresión relatástica, de manera que los calificadores “móviles” y “estacionarios” son ellos mismos relativos. Los campos eléctricos son lo que se observaría en cualquiera de los dos cuadros. En los sistemas MQS, la densidad de flujo magnético\(\ \vec{B}\) es la misma en ambos cuadros.

El término relativo a la densidad de corriente pasa a ser:

\(\ \vec{E} \cdot \vec{J}=\left(\vec{E}^{\prime}-\vec{v} \times \vec{B}\right) \cdot \vec{J}\)

Podemos interpretar\(\ \vec{E}^{\prime} \cdot \vec{J}\) como disipación, pero el segundo término lleva un pequeño examen. Tenga en cuenta que está en forma de un producto vectorial triple (escalar):

\(\ -\vec{v} \times \vec{B} \cdot \vec{J}=-\vec{v} \cdot \vec{B} \times \vec{J}=-\vec{v} \cdot \vec{J} \times \vec{B}\)

Esto es en forma de velocidad por densidad de fuerza y representa la conversión de potencia de forma electromagnética a mecánica. Esto es consistente con la ley de fuerza de Lorentz (también observada experimentalmente):

\(\ \vec{F}=\vec{J} \times \vec{B}\)

Esta última expresión es otra forma más de describir los procesos de conversión de energía en la maquinaria eléctrica, ya que el componente del campo eléctrico aparente producido por el movimiento material a través de un campo magnético, cuando reacciona contra una corriente, produce conversión de energía a forma mecánica en lugar de disipación.

Problemas adicionales en los métodos energéticos

Hay dos temas más importantes e interesantes a considerar a medida que estudiamos el desarrollo de fuerzas de origen electromagnético y su cálculo utilizando métodos energéticos. Estas se refieren a situaciones que no son simplemente representables por parámetros agrupados y situaciones que involucran imanes permanentes.

Coenergía en Medios Continuos

Considere un sistema con no solo una multiplicidad de circuitos sino un continuo de trayectorias portadoras de corriente. En ese caso podríamos identificar la coenergía como:

\(\ W_{m}^{\prime}=\int_{\text {area }} \int \lambda(\vec{a}) d \vec{J} \cdot d \vec{a}\)

donde se elige esa área para cortar todos los conductores portadores de corriente. Esta área puede ser escogida para ser perpedicular a cada uno de los filamentos actuales ya que la divergencia de corriente es cero. El flujo\(\ \lambda\) se calcula sobre una trayectoria que coincide con cada filamento de corriente (tales trayectorias existen ya que la corriente tiene divergencia cero). Entonces el flujo es:

\(\ \lambda(\vec{a})=\int \vec{B} \cdot d \vec{n}\)

Ahora bien, si usamos el potencial vectorial\(\ \vec{A}\) para el cual la densidad de flujo magnético es:

\(\ \vec{B}=\nabla \times \vec{A}\)

el flujo unido por cualquiera de los filamentos actuales es:

\(\ \lambda(\vec{a})=\oint \vec{A} \cdot d \vec{\ell}\)

Ahora: es posible hacer\(\ d \vec{\ell}\) coincidir\(\ d \vec{a}\) y ser paralelos a los filamentos actuales, de manera que:

\(\ W_{m}^{\prime}=\int_{\mathrm{Vol}} \vec{A} \cdot d \vec{J} d v\)

Imanes Permanentes

Los imanes permanentes se están convirtiendo en un elemento aún más importante en los sistemas de máquinas eléctricas. A menudo, los sistemas con imanes permanentes son abordados de una manera relativamente ad-hoc, hechos equivalentes a una corriente que produce el mismo MMF que el propio imán.

La relación constitutiva para un imán permanente relaciona la densidad de flujo magnético\(\ \vec{B}\) con el campo magnético\(\ \vec{H}\) y la propiedad del propio imán, la magnetización\(\ \vec{M}\).

\(\ \vec{B}=\mu_{0}(\vec{H}+\vec{M})\)

Ahora bien, el efecto de la magnetización es actuar como si hubiera una corriente (llamada corriente amperiana) con densidad:

\(\ \vec{J}^{*}=\nabla \times \vec{M}\)

Tenga en cuenta que esta corriente de amperios “actúa” igual que la corriente ordinaria al hacer densidad de flujo magnético. La coenergía magnética es:

\(\ W_{m}^{\prime}=\int_{\mathrm{vol}} \vec{A} \cdot \nabla \times d \vec{M} d v\)

A continuación, anote la identidad del vector

\(\ \nabla \cdot(\vec{C} \times \vec{D})=\vec{D} \cdot(\nabla \times \vec{C})-\vec{C} \cdot(\nabla \times \vec{D})\)

Para que:

\(\ W_{m}^{\prime}=\int_{\mathrm{vol}}-\nabla \cdot(\vec{A} \times d \vec{M}) d v+\int_{\mathrm{vol}}(\nabla \times \vec{A}) \cdot d \vec{M} d v\)

Después, señalando que\(\ \vec{B}=\nabla \times \vec{A}\):

\(\ W_{m}^{\prime}=-\oiint \vec{A} \times d \vec{M} d \vec{s}+\int_{\mathrm{vol}} \vec{B} \cdot d \vec{M} d v\)

La primera de estas integrales (superficie cerrada) desaparece si se toma sobre una superficie justo fuera del imán, donde\(\ \vec{M}\) es cero. Así, la coenergía magnética en un sistema con solo una fuente de imán permanente es

\(\ W_{m}^{\prime}=\int_{\mathrm{VOl}} \vec{B} \cdot d \vec{M} d v\)

La adición de bobinas portadoras de corriente a dicho sistema se realiza de la manera obvia.

Descripción de la máquina eléctrica:

En realidad, esta descripción muestra un motor de inducción convencional. Este es un tipo muy común de máquina eléctrica y servirá como punto de referencia. La mayoría de las otras máquinas eléctricas funcionan de una manera que es la misma que la máquina de inducción o que difieren en formas que son fáciles de hacer referencia a la máquina de inducción.

Considere el dibujo simplificado de la máquina que se muestra en la Figura 3. La mayoría (¡pero no todos!) máquinas que vamos a estudiar tienen esencialmente esta morfología. El rotor de la máquina está montado sobre un eje que está soportado sobre algún tipo de rodamiento (s). Por lo general, pero no siempre, el rotor está dentro. He dibujado un rotor que es redondo, pero este no tiene por qué ser el caso. También he indicado conductores de rotor, pero a veces el rotor tiene imanes permanentes ya sea sujetos a él o dentro, y a veces (como en Máquinas de reluctancia Variable) es solo una pieza de acero de forma extraña. El estator está, en este dibujo, en el exterior y tiene devanados. Con la mayoría de las máquinas con las que trataremos, el devanado del estator es la armadura, o elemento de entrada de energía eléctrica. (En motores DC y Universal esto se invierte, con la armadura contenida en el rotor: trataremos de estos más adelante).

En la mayoría de las máquinas eléctricas el rotor y el estator están hechos de materiales altamente permeables magnéticamente: acero o hierro magnético. En muchas máquinas comunes como los motores de inducción, el rotor y el estator están compuestos ambos de láminas delgadas de acero al silicio. Perforadas en esas hojas hay ranuras que contienen los conductores del rotor y del estator.

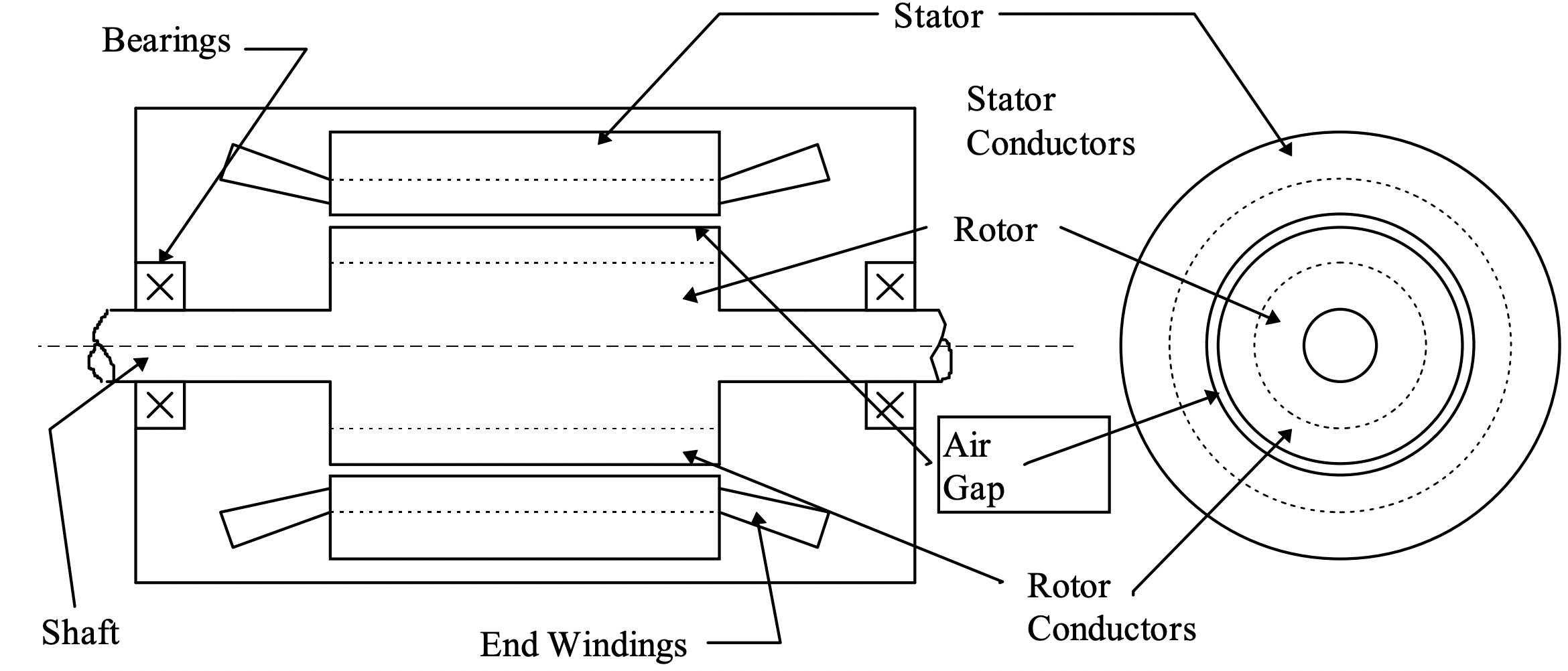Figura 3: Forma de la máquina eléctrica

La Figura 4 es una imagen de parte de una máquina de inducción distorsionada de manera que se endereza el entrehierro (como si la máquina tuviera radio infinito). Esta es en realidad una forma conveniente de dibujar la máquina y, encontraremos, conduce a métodos útiles de análisis.

Lo que es importante tener en cuenta por ahora es que la máquina tiene un entrehierro g que es relativamente pequeño (es decir, la dimensión del espacio es mucho menor que el radio de la máquina r). La máquina también tiene una longitud física l. La máquina eléctrica funciona produciendo un esfuerzo cortante en el entrehierro (con, por supuesto, efectos secundarios como la producción de “contratensión”). Es posible definir el esfuerzo cortante promedio del entrehierro, al que nos referiremos como\(\ \tau\). El par total desarrollado es la fuerza sobre el área de superficie por el momento (que es el radio del rotor):

\(\ T=2 \pi r^{2} \ell<\tau>\)

La potencia transferida por este dispositivo es solo par por velocidad, que es lo mismo que la fuerza por velocidad superficial, ya que la velocidad superficial es\(\ u=r \Omega\):

\(\ P_{m}=\Omega T=2 \pi r \ell<\tau>u\)

Si observamos que el volumen activo del rotor es\(\ \pi r^{2} \ell\), la relación entre el par y el volumen es solo:

\(\ \frac{T}{V_{r}}=2<\tau>\)

Ahora, determinar qué se puede hacer en un volumen de máquina implica dos cosas. En primer lugar, es claro que el volumen que hemos calculado aquí no es el volumen completo de la máquina, ya que no incluye el estator. La estimación real del volumen total de la máquina a partir del volumen del rotor es en realidad bastante compleja y detallada y dejaremos esa para más adelante. Segundo, necesitamos estimar el valor del esfuerzo cortante promedio útil. Supongamos tanto la densidad de flujo radial Br como la densidad de corriente superficial del estator Kz son ondas de flujo sinusoidales de la forma:

\(\ B_{r}=\sqrt{2} B_{0} \cos (p \theta-\omega t)\)

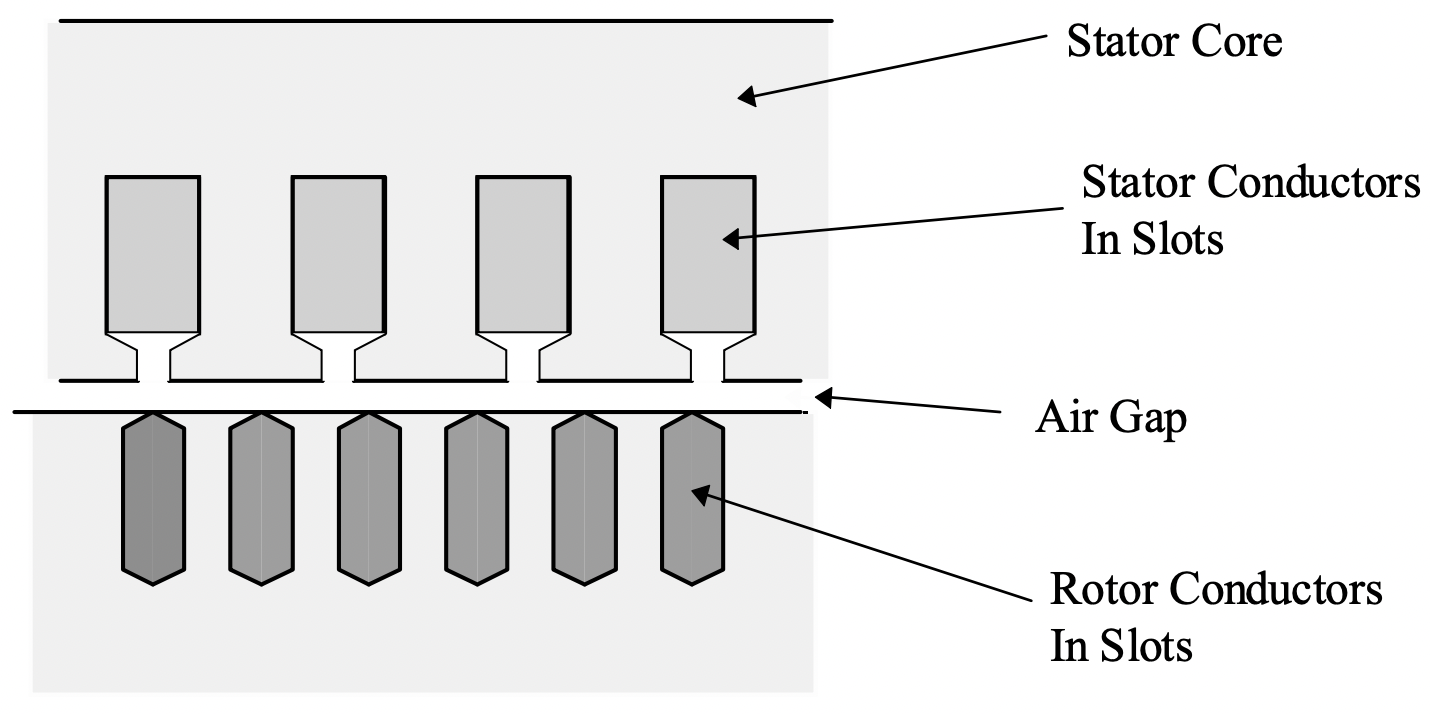Figura 4: Bobinas en Ranuras

\(\ K_{z}=\sqrt{2} K_{0} \cos (p \theta-\omega t)\)

Tenga en cuenta que esto supone que estas dos cantidades están exactamente en fase, u orientadas a producir idealmente torque, por lo que vamos a conseguir un límite “optimista” aquí. Entonces el valor promedio de tracción superficial es:

\(\ <\tau>=\frac{1}{2 \pi} \int_{0}^{2 \pi} B_{r} K_{z} d \theta=B_{0} K_{0}\)

Esto realmente tiene cierto sentido en vista de la Ley de Fuerza Lorentz derivada empíricamente: Dada una densidad de corriente (vector) y una densidad de flujo (vector). En ausencia de materiales magnéticos (aquellos con permeabilidad diferente a la del espacio libre), la fuerza observada sobre un conductor es:

\(\ \vec{F}=\vec{J} \times \vec{B}\)

Dónde\(\ \vec{J}\) está el vector que describe la densidad de corriente\(\ \left(A / m^{2}\right)\) y\(\ \vec{B}\) es la densidad de flujo magnético (T). Esto en realidad es suficiente para describir las fuerzas que vemos en muchas máquinas, pero como las máquinas eléctricas tienen material magnético permeable y dado que los campos magnéticos producen fuerzas sobre el material permeable incluso en ausencia de corrientes macroscópicas es necesario observar cómo aparece la fuerza sobre dicho material. Una expresión empírica adecuada para la densidad de fuerza es:

\(\ \vec{F}=\vec{J} \times \vec{B}-\frac{1}{2}(\vec{H} \cdot \vec{H}) \nabla \mu\)

donde\(\ \vec{H}\) está la intensidad del campo magnético y\(\ \mu\) es la permeabilidad.

Ahora, tenga en cuenta que la densidad de corriente es el rizo de la intensidad del campo magnético, de manera que

\ (\\ comenzar {alineado}
\ vec {F} & =(\ nabla\ veces\ vec {H})\ veces\ mu\ vec {H} -\ frac {1} {2} (\ vec {H}\ cdot\ vec {H})\ nabla\ mu\
&=\ mu (\ nabla\ veces\ vec {H})\ veces\ c {H} -\ frac {1} {2} (\ vec {H}\ cdot\ vec {H})\ nabla\ mu
\ end {alineado}\)

Y, ya que:

\(\ (\nabla \times \vec{H}) \times \vec{H}=(\vec{H} \cdot \nabla) \vec{H}-\frac{1}{2} \nabla(\vec{H} \cdot \vec{H})\)

densidad de fuerza es:

\ (\\ comenzar {alineado}
\ vec {F} &=\ mu (\ vec {H}\ cdot\ nabla)\ vec {H} -\ frac {1} {2}\ mu\ nabla (\ vec {H}\ cdot\ vec {H}) -\ frac {1} {2} (\ vec {H}\ cdot\ vec {H})\ nabla\ mu\\
&=\ mu (\ vec {H}\ cdot\ nabla)\ vec {H} -\ nabla\ izquierda (\ frac {1} {2}\ mu (\ vec {H}\ cdot\ vec {H})\ derecha)
\ end { alineado}\)

Esta expresión puede ser escrita por componentes: el componente de fuerza en la dimensión i'ésima es:

\(\ F_{i}=\mu \sum_{k}\left(H_{k} \frac{\partial}{\partial x_{k}}\right) H_{i}-\frac{\partial}{\partial x_{i}}\left(\frac{1}{2} \mu \sum_{k} H_{k}^{2}\right)\)

Ahora, vea que podemos escribir la divergencia de la densidad de flujo magnético como:

\(\ \nabla \cdot \vec{B}=\sum_{k} \frac{\partial}{\partial x_{k}} \mu H_{k}=0\)

y

\(\ \mu \sum_{k}\left(H_{k} \frac{\partial}{\partial x_{k}}\right) H_{i}=\sum_{k} \frac{\partial}{\partial x_{k}} \mu H_{k} H_{i}-H_{i} \sum_{k} \frac{\partial}{\partial x_{k}} \mu H_{k}\)

pero como el último término en eso es cero, podemos escribir densidad de fuerza como:

\(\ F_{k}=\frac{\partial}{\partial x_{i}}\left(\mu H_{i} H_{k}-\frac{\mu}{2} \delta_{i k} \sum_{n} H_{n}^{2}\right)\)

donde hemos usado el delta de Kroneker\(\ \delta_{i k}=1\) si\(\ i=k\), 0 en caso contrario.

Tenga en cuenta que esta densidad de fuerza está en la forma de la divergencia de un tensor:

\(\ F_{k}=\frac{\partial}{\partial x_{i}} T_{i k}\)

o

\(\ \vec{F}=\nabla \cdot \underline{\underline{T}}\)

En este caso, la fuerza sobre algún objeto que puede estar rodeado por una superficie cerrada se puede encontrar usando el teorema de divergencia:

\(\ \vec{f}=\int_{\mathrm{vol}} \vec{F} d v=\int_{\mathrm{vol}} \nabla \cdot \underline{\underline{T}} d v=\oiint \underline{\underline{T}} \cdot \vec{n} d a\)

o, si observamos que la tracción superficial es\(\ \tau_{i}=\sum_{k} T_{i k} n_{k}\), donde n es el vector normal de superficie, entonces la fuerza total en la dirección i es solo:

\(\ \vec{f}=\oint_{s} \tau_{i} d a=\oint \sum_{k} T_{i k} n_{k} d a\)

La interpretación de todo esto es menos difícil de lo que sugiere la notación. Esta descripción de campo de las fuerzas nos da una imagen simple de la tracción superficial, la fuerza por unidad de área sobre una superficie. Si solo integramos esta tracción sobre el área de algún cuerpo obtenemos toda la fuerza sobre el cuerpo. Tenga en cuenta que esto funciona si integramos la tracción sobre una superficie que se encuentra en sí misma en el espacio libre pero que rodea el cuerpo (porque no podemos imponer fuerza sobre el espacio libre).

Anote una cosa más sobre esta notación. En ocasiones, cuando los subíndices se repiten tal como están aquí se omite el símbolo de suma. Así escribiríamos\(\ \tau_{i}=\sum_{k} T_{i k} n_{k}=T_{i k} n_{k}\).

Ahora bien, si volvemos al caso de un cilindro circular y estamos interesados en el par, es bastante claro que podemos calcular la fuerza circunferencial señalando que el vector normal al cilindro es solo el vector de unidad radial, y entonces la tracción circunferencial debe ser simplemente:

\(\ \tau_{\theta}=\mu_{0} H_{r} H_{\theta}\)

La simple integración de esto sobre la superficie da fuerza acimutal, y luego multiplicar por radio (brazo de momento) da par. El último paso es señalar que, si el rotor está hecho de material altamente permeable, el campo magnético azimutal es igual a la densidad de corriente superficial.