2.4: Susceptibilidad dieléctrica
- Page ID
- 84818
Si el campo del incidente es monofrecuente, i.e.
\[\vec{E} (t)^{(+)} = \hat{\vec{E}} e^{i\omega t},\label{eq2.4.1} \]
y suponiendo que la inversión\(w\) del átomo estará bien representada por su promedio de tiempo\(w_s\), entonces el momento dipolar oscilará con la misma frecuencia en el estado estacionario
\[d = \hat{d} e^{i\omega t},\label{eq2.4.2} \]
y la inversión se ajustará a un nuevo valor estacionario\(w_s\). Con ansatz (\(\ref{eq2.4.1}\)) y (\(\ref{eq2.4.2}\)) en Eqs. (2.3.98) y (2.3.99), obtenemos
\[\hat{d} = \dfrac{-j}{2\hbar} \dfrac{w_s}{1/T_2 + j(\omega - \omega_{eg})} \vec{M} \hat{\vec{E}},\label{eq2.4.3} \]
\[w_s = \dfrac{w_0}{1 + \tfrac{T_1}{\hbar^2} \tfrac{1/T_2 |\vec{M} \hat{\vec{E}}|^2}{(1/T_2)^2 + (\omega_{eg} - \omega)^2}}. \nonumber \]
Introducimos la función de forma de línea normalizada, que es en este caso una lorentziana,
\[L(\omega) = \dfrac{(1/T_2)^2}{(1/T_2)^2 + (\omega_{eg} - \omega)^2}, \nonumber \]
y conectar el cuadrado del campo\(|\hat{\vec{E}}|^2\) a la intensidad\(I\) de una onda plana de propagación, de acuerdo con la Ecuación (2.2.27)\(I = \dfrac{1}{2Z_F} |\hat{\vec{E}}|^2\),
\[w_s = \dfrac{w_0}{1 + \tfrac{I}{I_s} L(\omega)}. \nonumber \]
Así la inversión estacionaria depende de la intensidad de la luz incidente, por lo tanto, se\(w_0\) puede llamar la inversión insaturada,\(w_s\) la inversión saturada y\(I_s\), con
\[I_s = \left [ \dfrac{2T_1T_2 Z_F}{\hbar^2} \dfrac{|\vec{M} \hat{\vec{E}}|^2}{|\hat{\vec{E}}|^2} \right ]^{-1}, \nonumber \]
es la intensidad de saturación. El valor de expectativa del operador dipolo viene dado entonces por
\[<\vec{p}>= -(\vec{M}^* d + \vec{M} d^*). \nonumber \]
La multiplicación con el número de átomos por unidad de volumen\(N\) relaciona el momento dipolar del átomo con la polarización compleja\(\hat{\vec{P}}^+\) del medio, y por lo tanto con la susceptibilidad según
\[\hat{\vec{P}}^{(+)} = -2N \vec{M}^* \hat{d},\label{eq2.4.9} \]
\[\hat{\vec{P}}^{(+)} = \epsilon_x \chi (\omega) \hat{\vec{E}}.\label{eq2.4.10} \]
De las definiciones (\(\ref{eq2.4.9}\)), (\(\ref{eq2.4.10}\)) y Ecuación (\(\ref{eq2.4.2}\)) obtenemos para la susceptibilidad lineal del medio
\[\chi (\omega) = \vec{M}^* \vec{M}^T \dfrac{jN}{\hbar \epsilon_0} \dfrac{w_s}{1/T_2 + j(\omega - \omega_{eg})}. \nonumber \]
que es un tensor. A continuación asumimos que la dirección del átomo es aleatoria, es decir, la alineación del momento dipolo atómico\(\vec{M}\) y el campo eléctrico es aleatoria. Por lo tanto, tenemos que promediar sobre el ángulo encerrado entre el campo eléctrico de la onda y el momento dipolo atómico, lo que resulta en
\[\overline{\left (\begin{matrix} M_x M_x & M_x M_y & M_x M_z \\ M_y M_x & M_y M_y & M_y M_z \\ M_z M_x & M_z M_y & M_z M_z \end{matrix} \right )} = \left (\begin{matrix} \overline{M_x^2} & 0 & 0 \\ 0 & \overline{M_y^2} & 0 \\ 0 & 0 & \overline{M_y^2} \end{matrix} \right ) = \dfrac{1}{3} |\vec{M}|^2 1. \nonumber \]
Así, para medios homogéneos e isotrópicos el tensor de susceptibilidad se contrae a un escalar
\[\chi (\omega) = \dfrac{1}{3} |\vec{M}|^2 \dfrac{jN}{\hbar \epsilon_0} \dfrac{w_s}{1/T_2 + j (\omega - \omega_{eg})}. \nonumber \]
Parte real e imaginaria de la susceptibilidad
\[\chi (\omega) = \chi ' (\omega) + j \chi '' (\omega) \nonumber \]
luego son dadas por
\[\chi '(\omega) = -\dfrac{|\vec{M}|^2 N w_s T_2^2 (\omega_{eg} - \omega)}{3\hbar \epsilon_0} L(\omega), \nonumber \]
\[\chi '' (\omega) = \dfrac{|\vec{M}|^2 N w_s T_s}{3 \hbar \epsilon_0} L(\omega). \nonumber \]
Si la radiación incidente es lo suficientemente débil, i.e.
\[T_1 T_2 \dfrac{|\vec{M}^* \hat{\vec{E}}|^2}{\hbar^2} L(\omega) \ll 1 \nonumber \]
obtenemos\(w_s \approx w_0\). Ya que\(w_0 < 0\), y especialmente para las transiciones ópticas\(w_0 = -1\), se muestran parte real e imaginaria de la susceptibilidad en la Figura 2.4.
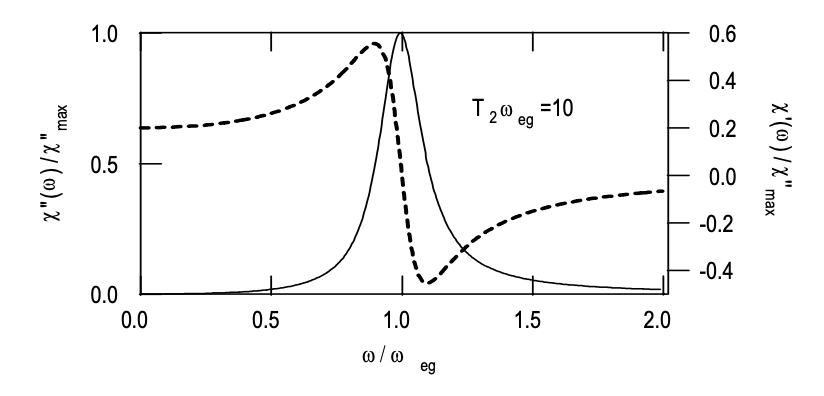
La susceptibilidad calculada cuántica mecánicamente se compara bien con la susceptibilidad clásica derivada del modelo de oscilador armónico cercano a la frecuencia de tránsito para una transición con razonablemente alta\(Q = T_2\omega_{ab}\). Tenga en cuenta que hay una desviación apreciable lejos de la resonancia. Lejos de la resonancia, no se debe utilizar la aproximación de onda giratoria.
El significado físico de la parte real e imaginaria de la susceptibilidad se hace evidente, cuando se considera la propagación de una onda electromagnética plana a través de este medio,
\[\vec{E} (z, t) = \Re \{ \hat{\vec{E}} e^{j(\omega t - kz)} \}, \nonumber \]
que se propaga en la\(z\) dirección positiva. La constante de propagación\(k\) está relacionada con la susceptibilidad por
\[k = \omega \sqrt{\mu_0 \epsilon_0 (1 + \chi (\omega))} \approx k_0 \left (1 + \dfrac{1}{2} \chi (\omega) \right ), \text{ with } k_0 = \omega \sqrt{\mu_0 \epsilon_0} \nonumber \]
para\(|\chi| \ll 1\). Bajo esta suposición obtenemos
\[k = k_0 (1 + \dfrac{\chi '}{2} ) + j k_0 \dfrac{\chi ''}{2}. \nonumber \]
La parte real de la susceptibilidad contribuye al índice de refracción\(n = 1 + \chi '/2\). En caso de\(\chi '' < 0\), la parte imaginaria conduce a una amortiguación exponencial de la ola. Para la\(\chi '' > 0\) amplificación se lleva a cabo. La amplificación de la onda es posible para\(w_0 > 0\), es decir, un medio invertido.
La tasa\(1/T_2\) de relajación de fase del momento dipolar determina el ancho de la línea de absorción o el ancho de banda del amplificador.