5.2: Bloqueo de modo activo por modulación de pérdida

El bloqueo de modo activo fue investigado por primera vez en 1970 por Kuizenga y Siegman usando un análisis de pulso gaussiano, que queremos delegar a los ejercicios [3]. Posteriormente en 1975 Haus [4] introdujo el enfoque de la ecuación maestra (5.1.21). Seguimos el enfoque de Haus, porque también muestra la estabilidad de la solución.

Imagen eliminada debido a restricciones de derechos de autor. Consulte: Keller, U., Física láser ultrarrápida, Instituto de Electrónica Cuántica, Instituto Federal Suizo de Tecnología, ETH Hönggerberg—HPT, CH-8093 Zurich, Suiza.

Figura 5.3: Representación esquemática de la ecuación maestra para un láser activamente bloqueado en modo.

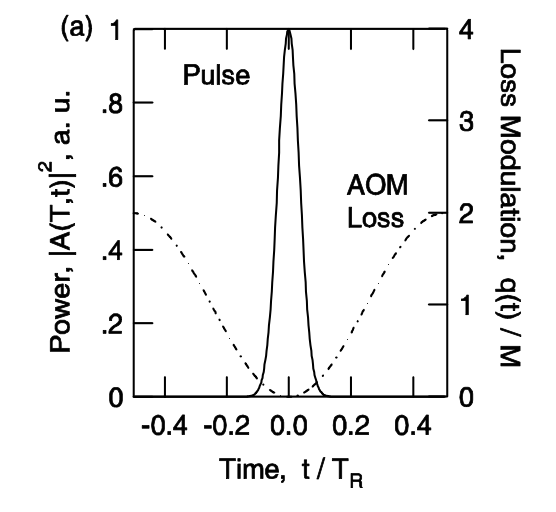
Introducimos un modulador de pérdida en la cavidad, por ejemplo un modulador acusto-óptico, que periódicamente varia la pérdida intracavitaria según\(q(t) = M(1- \cos (\omega_M t))\). La frecuencia de modulación tiene que ser sintonizada con mucha precisión al tiempo de ida y vuelta del resonador\(\omega_M = 2 \pi /T_R\), ver Figura 5.2. El proceso de modelocking se describe a continuación mediante la ecuación maestra

\[T_R \dfrac{\partial A}{\partial T} = \left [g(T) + D_g \dfrac{\partial^2}{\partial t^2} - l - M (1 - \cos (\omega_M t)) \right ] A.\label{eq5.2.1} \]

descuidando GDD y SPM. La ecuación puede interpretarse como la conformación total del pulso debido a ganancia, pérdida y modulador, ver Fig.5.3.

Si fijamos la ganancia en la Ecuación (\(\ref{eq5.2.1}\)) en su valor estacionario, lo que sea, la Ecuación (\(\ref{eq5.2.1}\)) es una p.d.e lineal, que puede resolverse mediante la separación de variables. Los pulsos, esperamos, tendrán un ancho mucho más corto que el tiempo de ida y vuelta TR. Se ubicarán en el mínimo de la modulación de pérdida donde la función coseno-función puede ser aproximada por una parábola y obtenemos

\[T_R \dfrac{\partial A}{\partial T} = \left [g - l + D_g \dfrac{\partial^2}{\partial t^2} - M_s t^2 \right ]A.\label{eq5.2.2} \]

\(M_s\)es la intensidad de modulación, y corresponde a la curvatura de la modulación de pérdida en el dominio del tiempo en el punto de pérdida mínima

\[D_g = \dfrac{g}{\Omega_g^2}, \nonumber \]

\[M_s = \dfrac{M \omega_M^2}{2}. \nonumber \]

El operador diferencial en el lado derecho de (\(\ref{eq5.2.2}\)) corresponde al operador Schrödinger-operador del problema del oscilador armónico. Por lo tanto, las funciones propias de este operador son los Ermite-Gaussians

\[A_n (T, t) = A_n (t) e^{\lambda_n T/ T_R},\label{eq5.2.5} \]

\[A_n (t) = \sqrt{\dfrac{W_n}{2^n \sqrt{\pi} n! \tau_a}} H_n (t/ \tau_a) e^{-\tfrac{t^2}{2\tau_a^2}}, \nonumber \]

donde\(\tau_a\) define el ancho del gaussiano. El ancho viene dado por la cuarta raíz de la relación entre la dispersión de ganancia y la intensidad del modulador

\[\tau_a = \sqrt[4]{D_g/M_s}.\label{eq5.2.7} \]

Obsérvese, de la Ecuación (\(\ref{eq5.2.5}\)) podemos seguir, que la ganancia por ida y vuelta de cada modo propio viene dada por\(\lambda_n\) (o en general la parte real de\(\lambda_n\)), que están dadas por

\[\lambda_n = g_n - l - 2M_s \tau_a^2 (n + \dfrac{1}{2}).\label{eq5.2.8} \]

La ganancia saturada correspondiente para cada solución eigen viene dada por

\[g_n = \dfrac{1}{1 + \tfrac{W_n}{P_L T_R}}, \nonumber \]

donde Wn es la energía de la solución correspondiente y\(P_L = E_L/\tau_L\) el poder de saturación de la ganancia. La ecuación (\(\ref{eq5.2.8}\)) muestra que para dada\(g\) la solución eigen con\(n = 0\), el modo tierra, tiene la mayor ganancia por ida y vuelta. Así, si inicialmente hay una distribución de campo que es una superposición de todas las soluciones propias, el modo tierra crecerá más rápido y saturará la ganancia a un valor

\[g_s = l + M_s \tau_a^2.\label{eq5.2.10} \]

tal que\(\lambda_0 = 0\) y en consecuencia todos los demás modos decaerán ya que\(\lambda_n < 0\) para\(n \ge 1\). Esto también demuestra la estabilidad de la solución de modo tierra [4]. Por lo tanto, el modeloqueo activo sin desintonizar entre el tiempo de ida y vuelta del resonador y el período del modulador conduce a pulsos de estado estacionario gaussiano con una anchura de

\[\Delta t_{FWHM} = 2 \ln 2 \tau_a = 1.66 \tau_a. \nonumber \]

El espectro del pulso gaussiano viene dado por

\[\tilde{A}_0 (\omega) = \int_{-\infty}^{\infty} A_0 (t) e^{i \omega t} dt \nonumber \]

\[= \sqrt{\sqrt{\pi} W_n \tau_a} e^{-\tfrac{(\omega \tau_a)^2}{2}}, \nonumber \]

y su FWHM es

\[\Delta f_{FWHM} = \dfrac{1.66}{2\pi \tau_a}. \nonumber \]

Por lo tanto, el producto tiempo-ancho de banda del gaussiano es

\[\Delta t_{FWHM} \cdot \Delta f_{FWHM} = 0.44. \nonumber \]

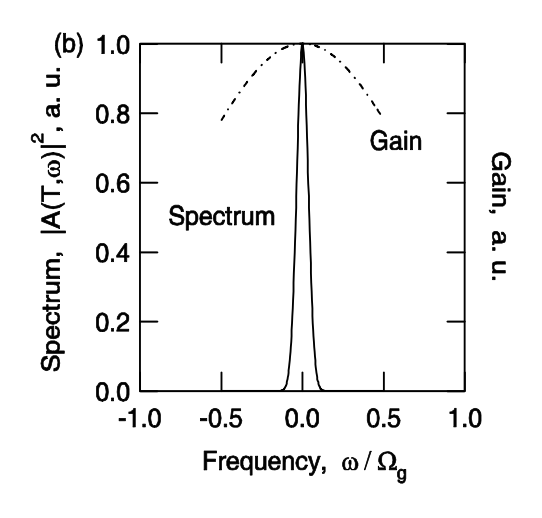
La forma de pulso estacionario del láser modelobloqueado se debe a la modulación de pérdida parabólica (acortamiento de pulso) en el dominio del tiempo y al filtrado parabólico (estiramiento de pulso) debido a la ganancia en el dominio de frecuencia, véanse las figuras 5.4 y 5.5. El pulso estacionario se logra cuando ambos efectos se equilibran. Dado que la modulación externa se limita a la velocidad electrónica y el ancho de pulso solo escala con la raíz cuadrada inversa del ancho de banda de ganancia, el modeloqueo activo, generalmente solo da como resultado un ancho de pulso en el rango de 10-100ps.

Figura 5.4: (a) La modulación de pérdida proporciona acortamiento del pulso en cada ida y vuelta

Figura 5.5: (b) el ancho de banda de ganancia finita da un ensanchamiento de pulso en cada ida y vuelta. Para un cierto ancho de pulso hay equilibrio entre los dos procesos.

Por ejemplo:\(\ce{Nd: YAG}\);\(2l = 2g = 10%\),\(\Omega_g = \pi \Delta f_{FWHM} = 0.65\) THz,\(M = 0.2\),\(f_m = 100\) MHz,\(D_g = 0.24 \ \text{ps}^2\),\(M_s = 4 \cdot 10^{16} s^{-1}\),\(\tau_p \approx 99 \ \text{ps}\).

Con el ancho de pulso (\(\ref{eq5.2.7}\)), la Ec. (\(\ref{eq5.2.10}\)) se puede reescribir de varias maneras

\[g_s = l + M_s \tau_a^2 = l + \dfrac{D_g}{\tau_a^2} = l + \dfrac{1}{2} M_s \tau_a^2 + \dfrac{1}{2} \dfrac{D_g}{\tau_a^2}, \nonumber \]

lo que significa que en estado estacionario la ganancia saturada se levanta por encima del nivel de pérdida l, de manera que muchos modos en el láser se mantienen por encima del umbral. Hay ganancia adicional necesaria para superar la pérdida del modulador debido al ancho temporal finito del pulso y el filtro de ganancia debido al ancho de banda finito del pulso. Por lo general

\[\dfrac{g_s - l}{l} = \dfrac{M_s \tau_a^2}{l} \ll 1, \nonumber \]

ya que los pulsos son mucho más cortos que el tiempo de ida y vuelta y la energía del pulso estacionario puede calcularse por lo tanto a

\[g_s = \dfrac{1}{1 + \tfrac{W_s}{P_L T_R}} = l. \nonumber \]

Figura 5.6: Modelocking en el dominio de frecuencia: El modulador traslada energía de cada modo a su modo vecino, redistribuyendo así la energía desde el centro a las alas del espectro. Este proceso siembra e inyección bloquea los modos vecinos.

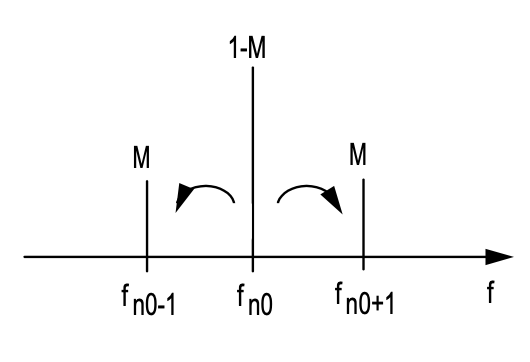
El nombre modelocking se origina a partir del estudio de este proceso de formación de pulsos en el dominio de frecuencia. Nota, el término

\[-M [1 - \cos (\omega_M t)] A \nonumber \]

genera bandas laterales en cada modo de cavidad presente de acuerdo con

\[\begin{array} {ll} \ & {-M[1 - \cos (\omega_M t)] \exp (j \omega_{n_0} t)} \\ = & {-M \left [\exp (j \omega_{n_0} t) - \dfrac{1}{2} \exp (j (\omega_{n_0} t - \omega_M t)) - \dfrac{1}{2} \exp (j (\omega_{n_0} t + \omega_M t))\right ]} \\ = & {M\left [-\exp(j \omega_{n_0} t) + \dfrac{1}{2}(j \omega_{n_0 - 1} t) + \dfrac{1}{2}(j \omega_{n_0 + 1} t) \right ]} \end{array} \nonumber \]

si la frecuencia de modulación es la misma que la frecuencia de ida y vuelta de la cavidad. Las bandas laterales generadas a partir de cada modo de ejecución se inyectan en los modos vecinos, lo que conduce a la sincronización y bloqueo de modos vecinos, es decir, bloqueo de modo, véase la Fig. 5.6