10.2: Autocorrelación Interferométrica (IAC)
- Page ID
- 84989
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Un método de caracterización de pulsos, que también revela la fase del pulso es la autocorrelación interferométrica introducida por J. C. Diels [2], (Figura 10.2 a). El haz de entrada se vuelve a dividir en dos y uno de ellos se retrasa. Sin embargo, ahora los dos pulsos se envían colinalmente al cristal no lineal. Solo se detecta el componente SHG después del filtro.
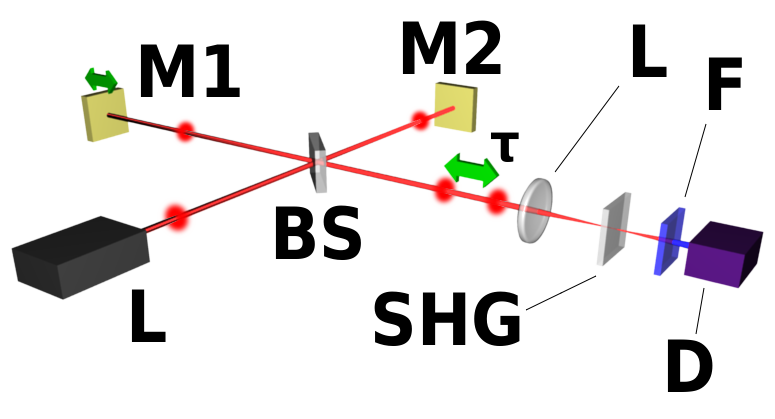
El campo total\(E(t,\tau)\) después del Interferómetro Michelson viene dado por los dos pulsos idénticos retardados uno\(\tau\) con respecto al otro
\[\begin{align*}E(t, \tau) &= E(t + \tau) + E(t) \\[4pt] &= A(t + \tau) e^{j\omega_c (t + \tau)} e^{j \phi_{CE}} + A(t) e^{j \omega_c t} e^{j \phi_{CE}}. \end{align*} \nonumber \]
A (t) es la amplitud compleja, el término\(e^{i\omega_0 t}\) describe la oscilación con la frecuencia portadora\(\omega_0\) y\(\phi_{CE}\) es la fase portadora envolvente. Ecuación (10.1.1) escribe
\[P^{(2)} (t, \tau) \propto (A(t + \tau) e^{j \omega_c (t + \tau)} e^{j \phi_{CE}} + A(t) e^{j \omega_c t} e^{j\phi_{CE}})^2 \nonumber \]
Esto sólo es ideal si los caminos para ambos haces son idénticos. Si por ejemplo se utilizan divisores de haz dieléctricos o metálicos, hay diferentes reflexiones involucradas en el Interferómetro Michelson mostrado en la Figura 10.2 (a) que conducen a un desplazamiento de fase diferencial entre los dos pulsos. Esto se puede evitar mediante una etapa de retardo exactamente simétrica como se muestra en la Figura 10.1 (b).
Nuevamente, el segundo campo eléctrico armónico irradiado es proporcional a la polarización
\[E(t, \tau) \propto (A(t + \tau) e^{j \omega_c (t + \tau)} e^{j \phi_{CE}} + A(t) e^{j \omega_c t} e^{j\phi_{CE}})^2 \nonumber \]
El fotodetector (o fotomultiplicador) se integra sobre la envolvente de cada pulso individual
\[\begin{array} {rcl} {I(\tau)} & \propto & {\int_{-\infty}^{\infty} |(A(t + \tau) e^{j\omega_c (t + \tau)} + A(t) e^{j\omega_c t})^2|^2 dt.} \\ {} & \propto & {\int_{-\infty}^{\infty} |A^2(t + \tau) e^{j 2 \omega_c (t + \tau)} + 2A(t + \tau) A(t) e^{j\omega_c (t + \tau)} e^{j \omega_c t} + A^2 (t) e^{j 2 \omega_c t}|^2.} \end{array} \nonumber \]
La evaluación del cuadrado absoluto conduce a la siguiente expresión
\[\begin{array} {rcl} {I(\tau)} & \propto & {\int_{-\infty}^{\infty} [|A(t + \tau)|^4 + 4|A(t + \tau)|^2 |A(t)|^2 + |A(t)|^4} \\ {} & \ & {+2A(t + \tau) |A(t)|^2 A^* (t) e^{j \omega_c \tau} + c.c.} \\ {} & \ & {+2A(t)|A(t + \tau)|^2 A^* (t + \tau) e^{-j \omega_c \tau} + c.c.} \\ {} & \ & {+A^2 (t + \tau) (A^* (t))^2 e^{j2\omega_c \tau} + c.c.]dt.} \end{array} \nonumber \]
La fase portador-envolvente\(\phi_{CE}\) cae ya que es idéntica a ambos pulsos. La función de autocorrelación interferométrica se compone de los siguientes términos
\[I(\tau) = I_{back} + I_{int} (\tau) + I_{\omega} (\tau) + I_{2 \omega} (\tau). \label{eq10.2.7} \]
Señal de fondo\(I_{back}\):
\[I_{back} = \int_{-\infty}^{\infty} (|A(t + \tau)|^4 + |A(t)|^4) dt = 2 \int_{-\infty}^{\infty} I^2 (t) dt \nonumber \]
Autocorrelación de intensidad\(I_{int} (\tau)\):
\[I_{int} (\tau) = 4\int_{-\infty}^{\infty} |A(t + \tau)|^2 |A(t)|^2 dt = 4 \int_{-\infty}^{\infty} I(t + \tau) \cdot I(t) dt \nonumber \]
Término de coherencia oscilante con\(\omega_c\)\(I_{\omega} (\tau)\):
\[I_{\omega} (\tau) = 4 \int_{-\infty}^{\infty} \text{Re} [(I(t) + I(t + \tau)) A^* (t) A(t + \tau) e^{j \omega \tau}] dt \nonumber \]
Término de coherencia oscilante con\(2 \omega_c\)\(I_{2\omega} (\tau)\):
\[I_{\omega} (\tau) = 2 \int_{-\infty}^{\infty} \text{Re} [A^2 (t) (A^* (t + \tau))^2 e^{j2\omega \tau}] dt \nonumber \]
La ecuación (\(\ref{eq10.2.7}\)) a menudo se normaliza en relación con la intensidad de fondo Iback dando como resultado la traza de autocorrelación interferométrica
\[I_{IAC} (\tau) = 1 + \dfrac{I_{int}(\tau)}{I_{back}} + \dfrac{I_{\omega}(\tau)}{I_{back}} + \dfrac{I_{2 \omega}(\tau)}{I_{back}}.\label{eq10.2.12} \]
La ecuación (\(\ref{eq10.2.12}\)) es la ecuación final para la autocorrelación interferométrica normalizada. El término\(I_{int} (\tau)\) es la autocorrelación de intensidad, medida por la generación de segundos armónicos no colineales como se discutió anteriormente. Por lo tanto, la autocorrelación interferométrica promediada da como resultado la autocorrelación de intensidad sentada sobre un fondo de 1.
La Figura 10.3 muestra un IAC calculado y medido para un pulso en forma de sech.
Imagen eliminada debido a restricciones de copyright. Consulte: Keller, U., Ultrafast Laser Physics, Instituto de Electrónica Cuántica, Instituto Federal Suizo de Tecnología, ETH Hönggerberg—HPT, CH-8093 Zurich, Suiza.
Figura 10.3: Trazas de autocorrelación interferométricas calculadas y medidas para un pulso de 10 fs de largo en forma de sech.
Al igual que con la autorcorrelación de intensidad, por construcción la autocorrelación interferométrica tiene que ser también simétrica:
\[I_{IAC} (\tau) = I_{IAC} (-\tau). \nonumber \]
Esto solo es cierto si la trayectoria del haz entre las dos réplicas en la configuración es completamente idéntica, es decir, ni siquiera hay un desplazamiento de fase entre los dos pulsos. Un desplazamiento de fase conduciría a un cambio en el patrón de franjas, que se manifiesta muy fuertemente en pulsos largos de pocos ciclos. Para evitar tal ruptura de simetría, se tiene que disponer la línea de retardo como se muestra en la Figura 10.2 b de manera que cada pulso viaje a través de la misma cantidad de material de sustrato y sufra las mismas reflexiones.
At\(\tau = 0\), todas las integrales son idénticas
\[\begin{array} {rcl} {I_{back}} & \equiv & {2 \int |A(t)|^4 dt} \\ {I_{int} (\tau = 0)} & \equiv & {2 \int |A^2(t)|^2 dt = 2 \int |A(t)|^4 dt = I_{back}} \\ {I_{\omega} (\tau = 0)} & \equiv & {2 \int |A(t)|^2 A(t) A^* (t) dt = 2 \int |A(t)|^4 dt = I_{back}}\\ {I_{2\omega} (\tau = 0)} & \equiv & {2\int A^2 (t) A^2 (t)^* dt = 2\int |A(t)|^4 dt = I_{back}} \end{array} \nonumber \]
Luego, obtenemos para la autocorrelación interferométrica con retardo de tiempo cero
\[\begin{array} {l} {I_{IAC} (\tau) |_{\max} = I_{IAC} (0) = 8} \\ {I_{IAC} (\tau \to \pm \infty) = 1} \\ {I_{IAC} (\tau) |_{\min} = 0} \end{array} \nonumber \]
Esta es la importante relación 1:8 entre las alas y la púa del IAC, que es una buena guía para la correcta alineación de un autocorrelacionador interferométrico. Para un pulso gorjeado el sobre ya no es real. Un chirp en el pulso da como resultado nodos en el IAC. La Figura 10.4 muestra el IAC de un pulso sech-chirped
\[A(t) = \left ( \text{sech} \left (\dfrac{t}{\tau_p}\right) \right )^{(1 + j\beta)}\nonumber \]
para diferentes chirps.
Imagen eliminada debido a restricciones de derechos de autor.
Consulte:
Keller, U., Física láser ultrarrápida, Instituto de Electrónica Cuántica, Instituto Federal Suizo de Tecnología, ETH Hönggerberg—HPT, CH-8093 Zurich, Suiza.
Figura 10.4: Influencia del aumento del chirrido en el CAI.
Autocorrelación interferométrica de un pulso de Sech-Pulso no Chirped
Envolvente de un pulso sech-pulso sin chirrido
\[A(t) = \text{sech} (t/\tau_p) \nonumber \]
Autocorrelación interferométrica de un pulso sech-pulso
\[I_{IAC} (\tau) = 1 + \{2 + \cos (2 \omega_c \tau) \} \dfrac{3((\tfrac{\tau}{\tau_p}) \cosh (\tfrac{\tau}{\tau_p}) - \sinh (\tfrac{\tau}{\tau_p}))}{\sinh^3 (\tfrac{\tau}{\tau_p})} + \dfrac{3(\sinh (\tfrac{2\tau}{\tau_p}) - (\tfrac{2\tau}{\tau_p}))}{\sinh^3 (\tfrac{\tau}{\tau_p})} \cos (\omega_c \tau) \nonumber \]
Autocorrelación interferométrica de un pulso gaussiano Chirped
Envolvente compleja de un pulso gaussiano
\[A(t) = \exp \left [-\dfrac{1}{2} \left (\dfrac{t}{t_p} \right ) (1 + j \beta) \right ]. \nonumber \]
Autocorrelación interferométrica de un pulso gaussiano
\[I_{IAC} (\tau) = 1 + \{2 + e^{-\tfrac{\beta^2}{2} (\tfrac{\tau}{\tau_p})^2} \cos (2 \omega_c \tau) \} e^{-\tfrac{1}{2} (\tfrac{\tau}{\tau_p})^2} + 4e^{-\tfrac{3+\beta^2}{8} (\tfrac{\tau}{\tau_p})^2} \cos \left (\dfrac{\beta}{4} \left (\dfrac{\tau}{\tau_p} \right )^2 \right ) \cos (\omega_c \tau). \nonumber \]
Dispersión de Segundo Orden
Es bastante sencillo calcular en el dominio de Fourier lo que sucede en presencia de dispersión.
\[E(t) = A(t) e^{j \omega_c t} \to \tilde{E} (\omega) \nonumber \]
Después de la propagación a través de un medio dispersivo se obtiene en el dominio de Fourier.
\[\tilde{E}' (\omega) = \tilde{E} (\omega) e^{-i\Phi (\omega)}\nonumber \]
y
\[E'(t) = A'9t) e^{j \omega_c t}\nonumber \]
La Figura 10.5 muestra la amplitud del pulso antes y después de la propagación a través de un medio con dispersión de segundo orden. El pulso se ensancha debido a la dispersión. Si la dispersión se incrementa aún más el ensanchamiento aumenta y las trazas de autocorrelación interferométrica mostradas en la Figura 10.5 desarrollan un pedestal característico debido al término\(I_{int}\). El ancho de la parte interferométricamente sensible sigue siendo el mismo y está más relacionado con el tiempo de coherencia en el pulso, es decir, proporcional al ancho espectral inverso y no cambia.
Imagen eliminada debido a restricciones de derechos de autor.
Consulte:
Keller, U., Física láser ultrarrápida, Instituto de Electrónica Cuántica, Instituto Federal Suizo de Tecnología, ETH Hönggerberg—HPT, CH-8093 Zurich, Suiza.
Figura 10.5: Efecto de diversas cantidades de dispersión de segundo orden sobre un pulso SECH de 10 fs limitado en forma trans.
Dispersión de tercer orden
Esperamos, que la dispersión de tercer orden afecte significativamente al pulso para
\[\dfrac{D_3}{\tau^3} > 1\nonumber \]
que es para un pulso sech-10fs\(D_3 > (\tfrac{10fs}{1.76})^3 183 fs^3\). Las figuras 10.6 y 10.7 muestran el impacto en la forma del pulso y la autocorrelación interferométrica. El término de dispersión impar genera asimetría en el pulso. La autocorrelación interferométrica desarrolla nodos característicos en las alas.
Imagen eliminada debido a restricciones de derechos de autor.
Por favor vea:
Keller, U., Física láser ultrarrápida, Instituto de Electrónica Cuántica, Instituto Federal Suizo de Tecnología, ETH Hönggerberg—HPT, CH-8093 Zurich, Suiza.
Figura 10.6: Impacto de 200 dispersiones de\(fs^3\) tercer orden en un pulso de 10 fs a una longitud de onda central de 800 nm.y su autocorrelación interferométrica.
Imagen eliminada debido a restricciones de derechos de autor.
Consulte:
Keller, U., Física láser ultrarrápida, Instituto de Electrónica Cuántica, Instituto Federal Suizo de Tecnología, ETH Hönggerberg—HPT, CH-8093 Zurich, Suiza.
Figura 10.7: Cambios debidos al aumento de la Dispersión de tercer orden de 100-1000\(fs^3\) en un pulso de 10 fs a una longitud de onda central de 800 nm.
Modulación autofásica
La modulación de autofase sin compensación por dispersión negativa adecuada genera una fase sobre el pulso en el dominio del tiempo. Esta fase es invisible en la autocorrelación de intensidad, sin embargo se muestra claramente en el IAC, ver Figura 10.8 para un pulso gaussiano con desplazamiento de fase no lineal pico\(\phi_0 = \delta A_0^2 = 2\) y Figura 10.8 para un desplazamiento de fase no lineal\(\phi_0 = 3\).
Imagen eliminada debido a restricciones de derechos de autor.
Consulte:
Keller, U., Física láser ultrarrápida, Instituto de Electrónica Cuántica, Instituto Federal Suizo de Tecnología, ETH Hönggerberg—HPT, CH-8093 Zurich, Suiza.
Figura 10.8: Cambio en la forma del pulso y autocorrelación interferométrica en un pulso de 10 fs a 800 nm sujeto a modulación de autofase pura que conduce a un desplazamiento de fase no lineal de\(\phi_0 = 2\).
Imagen eliminada debido a restricciones de derechos de autor.
Consulte:
Keller, U., Física láser ultrarrápida, Instituto de Electrónica Cuántica, Instituto Federal Suizo de Tecnología, ETH Hönggerberg—HPT, CH-8093 Zurich, Suiza.
Figura 10.9: Cambio en la forma del pulso y autocorrelación interferométrica en un pulso de 10 fs a 800 nm sujeto a modulación de autofase pura que conduce a un desplazamiento de fase no lineal de\(\phi_0 = 3\).
A partir de la experiencia obtenida al observar las trazas de IAC anteriores para pulsos sometidos a dispersiones de segundo y tercer orden, así como modulación de autofase, concluimos que en general es imposible predecir puramente mirando al IAC qué perturbaciones de fase podría tener un pulso. Por lo tanto, siempre fue un deseo reconstruir de manera única el campo eléctrico con respecto a la amplitud y fase a partir de los datos medidos. De hecho se puede demostrar rigurosamente, que la amplitud y la fase de un pulso pueden derivarse únicamente del IAC y el espectro medido hasta una ambigüitina de inversión de tiempo [1]. Además, se ha demostrado que una correlación cruzada del pulso con una réplica chirped en un medio conocido y el espectro del pulso es suficiente para reconstruir el pulso [3]. Dado que el espectro del pulso ya está dado solo se tiene que determinar la fase. Si se asume una determinada fase, se puede calcular el campo eléctrico y la correlación cruzada medida o IAC. La minimización del error entre la correlación cruzada medida o IAC dará la fase espectral de origen. Este procedimiento ha sido denominado PICASO (Fase e Intenisty de Correlación Cruzada y Espectro Solamente).
Tenga en cuenta que también en lugar de medir la autocorrelación y la autocorrelación interferométrica con SHG también se puede usar absorción de dos fotones o absorción de orden superior en un material semiconductor (Láser o LED) [4].
Sin embargo, hoy en día, las dos técnicas de cracterización de pulsos ampliamente utilizadas son la compuerta óptica de resolución de frecuencia (FROG) y la interferometría de fase espectral para la reconstrucción directa de campo eléctrico (SPID


