1.5: Reactancia e Impedancia
- Page ID
- 85937
A diferencia de una resistencia, el voltaje y la corriente no estarán en fase para un condensador ideal o para un inductor ideal. Para el condensador, la corriente conduce el voltaje a través del condensador 90 grados. Recordemos que el voltaje a través de un condensador no puede cambiar instantáneamente,\(i = C \, dv/dt\). Para un inductor, el voltaje conduce la corriente 90 grados. De igual manera, la corriente a través de un inductor no puede cambiar instantáneamente debido a\(v = L \, di/dt\). Si bien los capacitores e inductores ideales no exhiben resistencia, el voltaje reacciona a la corriente. Como era de esperar, llamamos a esta reactancia característica y la denotamos con la letra\(X\). La reactancia, al igual que la resistencia, es una relación entre voltaje y corriente. Definimos la reactancia capacitiva como:
\[X_{C} = \frac{v_c}{i_c} \label{1.7} \]
Usando una onda sinusoidal simple con un valor pico de unidad,\(v_c = \sin 2\pi f t\), se\(i_c\) puede encontrar a partir de\(i = C \, dv/dt\). Recordemos de nuestro trabajo anterior que la derivada o pendiente de una onda sinusoidal es una onda coseno, que a su vez equivale a una onda sinusoidal desplazada en +90\(^{\circ}\).
\[i_c = C \frac{dv_c}{dt} \nonumber \]
\[i_c = C \frac{d \sin(2 \pi f t)}{dt} \nonumber \]
\[i_c = C \sin (2 \pi f t+90^{\circ}) \nonumber \]
Sustituyendo este resultado en la Ecuación 1.7 rinde:
\[X_C = \frac{v_c}{i_c} \nonumber \]
\[X_C = \frac{\sin (2 \pi f t)}{2 \pi f C \sin (2\pi f t+90^{\circ})} \nonumber \]
\[X_C = \frac{1}{2} \pi f C \angle −90^{\circ} \nonumber \]
O más directamente:
\[X_C =− j \frac{1}{2 \pi f C} \label{1.8} \]
En suma, si dividimos el voltaje sinusoidal del condensador por su corriente (ley de Ohm), obtenemos un valor con un ángulo de fase de −90\(^{\circ}\). Si bien el resultante es un valor óhmico, no puede clasificarse como una resistencia. En cambio, se le conoce como reactancia y se denota con la letra\(X\). Así podemos referirnos a la reactancia de un condensador\(X_C\),, como algún número en un ángulo de −90\(^{\circ}\), o más convenientemente, simplemente anteponemos\(−j\), como en\(X_C = −j75 \Omega\).
El caso para el inductor es similar y se deja como ejercicio. La reactancia inductiva,\(X_L\), se puede encontrar usando:
\[X_L=+ j 2 \pi f L \label{1.9} \]
Un ejemplo sería\(X_L = j68 \Omega\). Como se dijo, si bien no se puede agregar una resistencia directamente a una reactancia, las reactancias se pueden sumar siempre y cuando prestemos atención a las señales. Por ejemplo, si tenemos una reactancia capacitiva de\(−j60 \Omega\) en serie con una reactancia inductiva de\(j100 \Omega\), el resultado es\(j40 \Omega\). Esto se debe a que estos dos rubros están 180 grados desfasados entre sí, por lo que cancelan parcialmente. Recuerda, siempre suma o resta como elementos: real (resistencia) a real, e imaginario (reactancia) a imaginario.
Las ecuaciones\ ref {1.8} y\ ref {1.9} son notables porque la reactancia no es solo una función de la capacitancia o inductancia, sino también una función de la frecuencia. La reactancia de un inductor es directamente proporcional a la frecuencia mientras que la reactancia de un condensador es inversamente proporcional a la frecuencia. Las variaciones óhmicas de una\(20 \Omega\) resistencia, un condensador de 500\(\mu\) F y un inductor de 500\(\mu\) H a través de la frecuencia se muestran en la Figura\(\PageIndex{1}\).
Podemos ver que el valor de la resistencia no cambia con la frecuencia mientras que la reactancia inductiva aumenta con la frecuencia y la reactancia capacitiva disminuye.
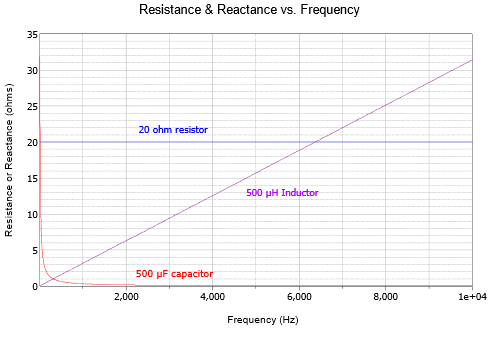
La escala de frecuencia lineal hace que el cambio de condensador sea difícil de ver. Si esto se vuelve a trazar pero usando una escala de frecuencia logarítmica como en la Figura\(\PageIndex{2}\), la simetría se vuelve aparente.
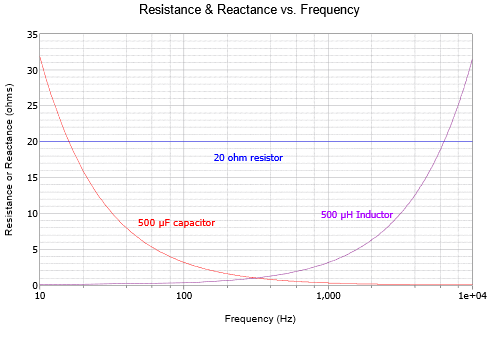
El efecto tanto del tamaño como de la frecuencia del condensador se muestra en la Figura\(\PageIndex{3}\) usando un eje de frecuencia logarítmica: cuanto más pequeño es el condensador, mayor es la reactancia capacitiva a cualquier frecuencia en particular.
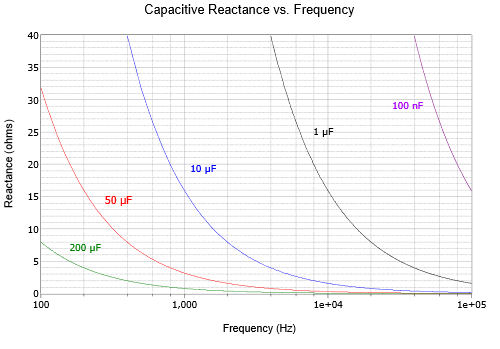
De manera similar, el efecto tanto del tamaño como de la frecuencia del inductor se muestra en la Figura\(\PageIndex{4}\) usando un eje de frecuencia lineal: cuanto mayor es el inductor, mayor es la reactancia inductiva a cualquier frecuencia dada.
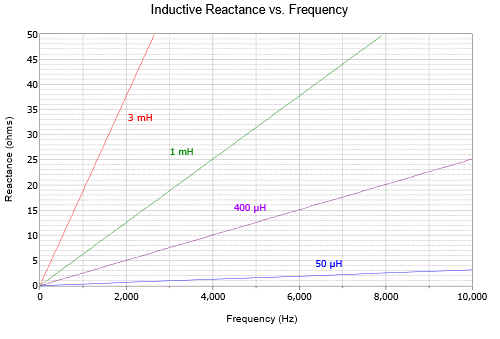
Vale la pena señalar que las parcelas de Figuras\(\PageIndex{3}\) y\(\PageIndex{4}\) son para componentes ideales. En realidad, todos los componentes exhiben algunos efectos resistivos, capacitivos e inductivos debido a su construcción. Por ejemplo, eventualmente, los efectos inductivos y resistivos harán que las curvas de reactancia capacitiva de la Figura\(\PageIndex{3}\) comiencen a subir a altas frecuencias. De igual manera, los efectos resistivos y capacitivos harán\(\PageIndex{4}\) que las curvas Figura se aplacen a frecuencias muy bajas y muy altas.
Una observación interesante para recordar es que los capacitores e inductores son un poco como una Quimera. Es decir, se ven como cosas diferentes a diferentes fuentes, todas machacadas a la vez. Sería impropio pensar, digamos, en un inductor particular como “tantos ohmios”. Si la señal fuente está compuesta por múltiples ondas sinusoidales, como una onda cuadrada o una forma de onda musical, el inductor “parece” un valor óhmico diferente a cada uno de los diferentes componentes de frecuencia, simultáneamente. Este es un concepto importante y uno que podemos aprovechar mucho, por ejemplo, en el diseño de circuitos de filtro.
Impedancia
Llegamos ahora a la impedancia. La impedancia es una mezcla de resistencia y reactancia, y se denota por\(Z\). Esto se puede visualizar como una combinación en serie de una resistencia y un condensador o un inductor. Los ejemplos incluyen\(Z = 100 − j50 \Omega\), es decir, 100 ohmios de resistencia en serie con 50 ohmios de reactancia capacitiva; y\(Z = 600\angle 45^{\circ} \Omega\), es decir, una magnitud de 600 ohmios que incluye resistencia y reactancia inductiva (debe ser reactancia inductiva y no reactancia capacitiva porque el signo del ángulo es positivo).
Para completar este sistema, contamos con susceptancia y admisión. La susceptancia,\(S\), es el recíproco de la reactancia. La admisión,\(Y\), es el recíproco de la impedancia. Estos son similares a la relación entre la conductancia y la resistencia, y son convenientes para combinaciones de circuitos paralelos.
Ejemplo\(\PageIndex{1}\)
Determinar las reactancias de un inductor de 1 mH y un condensador de 2\(\mu\) F a una onda sinusoidal de 2 kHz. Repita para una frecuencia de 50 kHz.
Usa Ecuaciones\ ref {1.8} y\ ref {1.9}. Para el condensador a 2 kHz tenemos:
\[X_C =− j \frac{1}{2\pi f C} \nonumber \]
\[X_C = − j \frac{1}{2 \pi 1kHz 2 \mu F} \nonumber \]
\[X_C =− j 79.6\Omega \nonumber \]
Para la segunda fuente, 50 kHz es 25 veces mayor que la original y la reactancia capacitiva es inversamente proporcional a la frecuencia. Por lo tanto\(X_C\) es 25 veces más pequeño, o\(−j3.18 \Omega\).
Para el inductor a 2 kHz,
\[X_L = +j 2\pi f L \nonumber \]
\[X_L = +j 2\pi 2 kHz 1 mH \nonumber \]
\[X L = +j 12.57\Omega \nonumber \]
La reactancia inductiva es directamente proporcional a la frecuencia. Así, aumentando f por un factor de 25 aumenta\(X_L\) por el mismo factor, resultando en\(j314.2 \Omega\).
Ejemplo\(\PageIndex{2}\)
Determinar la susceptancia de un inductor cuya reactancia es\(j400 \Omega\). Además, si este inductor se coloca en serie con una\(1000 \Omega\) resistencia, se determina la impedancia resultante en forma polar, así como la admitancia.
La susceptancia es el recíproco de la reactancia.
\[S_L = \frac{1}{X_L} \nonumber \]
\[S_L = \frac{1}{j 400\Omega} \nonumber \]
\[S_L = − j 2.5 \text{ millisiemens} \nonumber \]
La impedancia,\(Z\), es la suma vectorial, o\(1000 + j400 \Omega\). Convirtiendo esto en forma polar:
\[\text{Magnitude } = \sqrt{\text{Real}^2 + \text{Imaginary}^2} \nonumber \]
\[\text{Magnitude } = \sqrt{1000^2+400^2} \nonumber \]
\[\text{Magnitude } = 1077 \nonumber \]
\[\theta = \tan^{−1} \left( \frac{\text{Imaginary}}{\text{Real}} \right) \nonumber \]
\[\theta = \tan^{−1} \left( \frac{400}{1000} \right) \nonumber \]
\[\theta = 21.8^{\circ} \nonumber \]
El resultado es\(Z = 1077\angle 21.8^{\circ} \Omega\). El ingreso es el recíproco, cediendo\(Y = 928E-6\angle −21.8^{\circ} \mu S\).


