7.5: Amplificador de Base Común
- Page ID
- 83512
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)El tercer y último prototipo es el amplificador de base común. En esta configuración la señal de entrada se aplica al emisor y la salida se toma del colector. El terminal base está en el punto de tierra común. Un ejemplo, usando polarización de emisor de dos fuentes, se muestra en la Figura\(\PageIndex{1}\). Tenga en cuenta que debido a que ni la entrada ni la salida están conectadas a la base, no hay necesidad de una resistencia base. En consecuencia, el terminal base está conectado directamente a tierra.
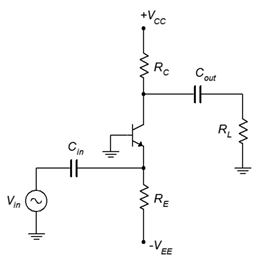
Figura\(\PageIndex{1}\): Amplificador de base común.
Algunas personas encuentran que redibujar el esquema horizontalmente ayuda a visualizar el flujo de la señal. Esta versión se muestra en la Figura\(\PageIndex{2}\).
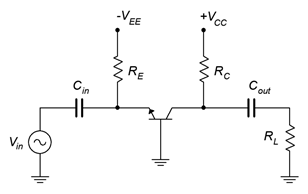
Figura\(\PageIndex{2}\): Amplificador de base común redibujado.
Una cosa buena de la versión horizontal es que cuando hacemos el equivalente de CA, se hace evidente que\(R_E\) está en paralelo con la entrada y\(R_C\) está en paralelo con la carga. Para el análisis de CA modificaremos la Figura\(\PageIndex{2}\) sustituyendo el modelo BJT por transistor, cortocircuitando los condensadores y llevando las fuentes de CC a tierra de CA. El resultado se muestra en la Figura\(\PageIndex{3}\).
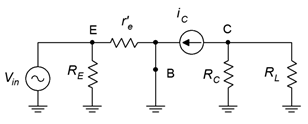
Figura\(\PageIndex{3}\): Amplificador base común con modelo BJT.
7.5.1: Ganancia de voltaje
Comenzamos con la definición básica de ganancia de voltaje y luego expandimos usando la ley de Ohm.
\[A_v = \frac{v_{out}}{v_{i n}} = \frac{v_C}{v_E} \\ A_v = \frac{i_C r_C}{i_E r'_e} \\ A_v = \frac{r_C}{r'_e} \label{7.13} \]
Esta ecuación es muy similar a la de un amplificador emisor común no inundado excepto que no invierta la señal de entrada. Por lo tanto, el potencial de ganancia es bastante alto.
7.5.2: Impedancia de entrada
La derivación para\(Z_{in}\) se obtiene mediante inspección directa del esquema.
\[Z_{in} = R_E || r'_e \label{7.14} \]
\(r'_e\)normalmente domina y así vemos que la configuración de base común tiende a tener una impedancia de entrada baja. Para las frecuencias de audio esto puede ser un problema pero es menos problemático a frecuencias más altas ya que, en términos generales, las impedancias del sistema necesitan ser menores para evitar complicaciones con efectos capacitivos.
7.5.3: Impedancia de salida
La derivación para\(Z_{out}\) sin cambios en comparación con la configuración del emisor común. La fórmula se repite a continuación para mayor comodidad.
\[Z_{out} \approx R_C \nonumber \]
Ejemplo\(\PageIndex{1}\)
Para el amplificador mostrado en la Figura\(\PageIndex{4}\), determine la ganancia de voltaje y la impedancia de entrada.
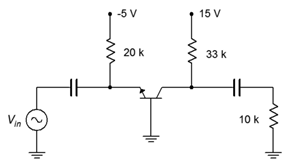
Figura\(\PageIndex{4}\): Esquemática por ejemplo\(\PageIndex{1}\).
\[I_C = \frac{∣V_{EE}∣−V_{BE}}{R_E} \nonumber \]
\[I_C = \frac{5V−0.7V}{20 k\Omega} \nonumber \]
\[I_C = 0.215mA \nonumber \]
\[r'_e = \frac{26mV}{I_C} \nonumber \]
\[r'_e = \frac{26 mV}{0.215mA} \nonumber \]
\[r'_e = 121\Omega \nonumber \]
\[Z_{i n} = r'_e || r_E \nonumber \]
\[Z_{i n} = 121\Omega || 20 k \Omega \nonumber \]
\[Z_{i n} = 120\Omega \nonumber \]
\[A_v = \frac{r_C}{r'_e} \nonumber \]
\[A_v = \frac{33k \Omega || 10 k\Omega}{120\Omega} \nonumber \]
\[A_v = 64 \nonumber \]


