2.5: Fuerza, Energía y Diferencia de Potencial en un Campo Magnético
- Page ID
- 83753
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)La fuerza\({\bf F}_m\) experimentada por una partícula en la ubicación que\({\bf r}\) lleva la carga\(q\) debido a un campo magnético es
\[{\bf F}_m = q {\bf v} \times {\bf B}({\bf r}) \label{m0059_eFm} \]
donde\({\bf v}\) es la velocidad (magnitud y dirección) de la partícula, y\({\bf B}({\bf r})\) es la densidad de flujo magnético en\({\bf r}\). Ahora debemos tener cuidado: En esta descripción, el movimiento de la partícula no se debe a\({\bf F}_m\). De hecho el producto cruzado en la Ecuación\ ref {M0059_efm} indica claramente que\({\bf F}_m\) y\({\bf v}\) debe estar en direcciones perpendiculares. En cambio, lo contrario es cierto: es decir, es el movimiento de la partícula lo que está dando origen a la fuerza. El movimiento descrito por\({\bf v}\) puede deberse a la presencia de un campo eléctrico, o simplemente puede ser que esa carga esté contenida dentro de una estructura que se encuentra en movimiento.
Sin embargo, la fuerza\({\bf F}_m\) tiene una energía potencial asociada. Además, esta energía potencial puede cambiar a medida que la partícula se mueve. Este cambio en la energía potencial puede dar lugar a una diferencia de potencial eléctrico (es decir, un “voltaje”), como ahora demostraremos.
El cambio en la energía potencial se puede cuantificar utilizando el concepto de trabajo,\(W\). El trabajo incremental\(\Delta W\) realizado al mover la partícula a una distancia corta\(\Delta l\), sobre el cual asumimos que el cambio en\({\bf F}_m\) es insignificante, es
\[\Delta W \approx {\bf F}_m\cdot\hat{\bf l}\Delta l \label{m0059_WeFdl} \]
donde en este caso\(\hat{\bf l}\) es el vector unitario en la dirección del movimiento; es decir, la dirección de\({\bf v}\). Tenga en cuenta que el propósito del producto de punto en la Ecuación\ ref {M0059_WefDL} es asegurar que solo el componente de\({\bf F}_m\) paralelo a la dirección del movimiento se incluya en el recuento de energía. Cualquier componente del\({\bf v}\) cual se deba a\({\bf F}_m\) (es decir, en última instancia debido a\({\bf B}\)) debe ser perpendicular a\({\bf F}_m\),\(\Delta W\) por lo que para tal contribución debe ser, de la Ecuación\ ref {M0059_WEFDL}, igual a cero. Es decir: En ausencia de una fuerza mecánica o de un campo eléctrico, la energía potencial de una partícula cargada permanece constante independientemente de cómo se mueva\({\bf F}_m\). Este sorprendente resultado puede resumirse de la siguiente manera:
El campo magnético no funciona.
En cambio, el cambio de energía potencial asociado con el campo magnético debe deberse completamente a un cambio de posición resultante de otras fuerzas, como una fuerza mecánica o la fuerza de Coulomb. La presencia de un campo magnético simplemente aumenta o disminuye esta diferencia de potencial una vez que la partícula se ha movido, y es este cambio en la diferencia de potencial lo que deseamos determinar.
Podemos hacer explícita la relación entre la diferencia de potencial y el campo magnético sustituyendo el lado derecho de la Ecuación\ ref {M0059_efm} en la Ecuación\ ref {M0059_WEFDL}, rindiendo
\[\Delta W \approx q \left[ {\bf v} \times {\bf B}({\bf r})\right] \cdot\hat{\bf l}\Delta l \label{m0059_WqEdl} \]
La ecuación\ ref {M0059_WQedL} da el trabajo solo para una corta distancia alrededor\({\bf r}\). Ahora intentemos generalizar este resultado. Si deseamos conocer el trabajo realizado a una distancia mayor, entonces debemos tener en cuenta la posibilidad que\({\bf v} \times {\bf B}\) varía a lo largo del camino tomado. Para ello, podemos sumar contribuciones de puntos a lo largo del camino trazado por la partícula, es decir,
\[W \approx \sum_{n=1}^N \Delta W ({\bf r}_n) \nonumber \]
donde\({\bf r}_n\) están las posiciones que definen el camino. Sustituyendo el lado derecho de la Ecuación\ ref {M0059_WQedL}, tenemos
\[W \approx q \sum_{n=1}^N \left[ {\bf v} \times {\bf B}({\bf r}_n) \right] \cdot\hat{\bf l}({\bf r}_n)\Delta l \nonumber \]
Tomando el límite como\(\Delta l\to 0\), obtenemos
\[W = q \int_{\mathcal C} \left[ {\bf v} \times {\bf B}({\bf r}) \right] \cdot\hat{\bf l}({\bf r}) dl \nonumber \]
donde\(\mathcal{C}\) está el camino (previamente, la secuencia\({\bf r}_n\) de's) seguido por la partícula. Ahora omitiendo la dependencia explícita\({\bf r}\) en el integrando para mayor claridad:
\[W = q \int_{\mathcal C} \left[ {\bf v} \times {\bf B} \right] \cdot d{\bf l} \label{m0059_eWqint} \]
donde\(d{\bf l} = \hat{\bf l}dl\) como de costumbre. Ahora, somos capaces de determinar el cambio en la energía potencial para una partícula cargada que se mueve a lo largo de cualquier trayectoria en el espacio, dado el campo magnético.
En este punto, es conveniente introducir la diferencia de potencial eléctrico\(V_{21}\) entre el punto de inicio (1) y el punto final (2) de\({\mathcal C}\). \(V_{21}\)se define como el trabajo realizado al atravesar\({\mathcal C}\), por unidad de carga; es decir,
\[V_{21} \triangleq \frac{W}{q} \nonumber \]
Este tiene unidades de J/C, que es voltios (V). Sustituyendo la ecuación\ ref {M0059_EWQint}, obtenemos:
\[\boxed{ V_{21} = \int_{\mathcal C} \left[ {\bf v} \times {\bf B} \right] \cdot d{\bf l} } \label{m0059_eVAB} \]
La ecuación\ ref {M0059_EVAB} es el potencial eléctrico inducido por la carga que atraviesa un campo magnético.
La figura\(\PageIndex{1}\) muestra un escenario sencillo que ilustra este concepto.

Aquí, un cable recto perfectamente conductor de longitud\(l\) es paralelo al\(y\) eje y se mueve a velocidad\(v\) en la\(+z\) dirección a través de un campo magnético\({\bf B}=\hat{\bf x}B\). Por lo tanto,
\[\begin{align} {\bf v} \times {\bf B} &= \hat{\bf z}v \times \hat{\bf x}B \nonumber \\ &= \hat{\bf y} B v\end{align} \nonumber \]
Tomando los puntos finales 1 y 2 del alambre para estar en\(y=y_0\) y\(y=y_0+l\), respectivamente, obtenemos
\[\begin{align} V_{21} &= \int_{y_0}^{y_0+l} \left[ \hat{\bf y} B v \right] \cdot \hat{\bf y}dy \nonumber \\ &= Bvl\end{align} \nonumber \]
Así, vemos que el punto final 2 está a un potencial eléctrico\(Bvl\) mayor que el del punto final 1. Este “voltaje” existe a pesar de que el cable es perfectamente conductor y, por lo tanto, no se puede atribuir al campo eléctrico. Este voltaje existe a pesar de que la fuerza requerida para el movimiento debe ser la misma en ambos puntos finales, o incluso podría ser cero, y por lo tanto no puede atribuirse a fuerzas mecánicas. En cambio, este cambio de potencial se debe enteramente al campo magnético.
Debido a que el cable no forma un bucle cerrado, no fluye corriente en el cable. Por lo tanto, este escenario tiene una aplicación limitada en la práctica. Para lograr algo útil con este concepto debemos al menos formar un bucle cerrado, para que la corriente pueda fluir. Para un bucle cerrado, la Ecuación\ ref {M0059_EVAB} se convierte en:
\[V = \oint_{\mathcal C} \left[ {\bf v} \times {\bf B} \right] \cdot d{\bf l} \label{m0059_eVABc} \]
El examen de esta ecuación indica un requisito adicional:\({\bf v} \times {\bf B}\) debe variar de alguna manera\(\mathcal{C}\). Esto se debe a\({\bf v} \times {\bf B}\) que si no varía sobre\(\mathcal{C}\), el resultado será
\[\left[ {\bf v} \times {\bf B} \right] \cdot \oint_{\mathcal C} d{\bf l} \nonumber \]
que es cero porque la integral es cero. El siguiente ejemplo demuestra una aplicación práctica de esta idea.
La figura\(\PageIndex{2}\) muestra una modificación del problema considerado originalmente en la figura\(\PageIndex{1}\).
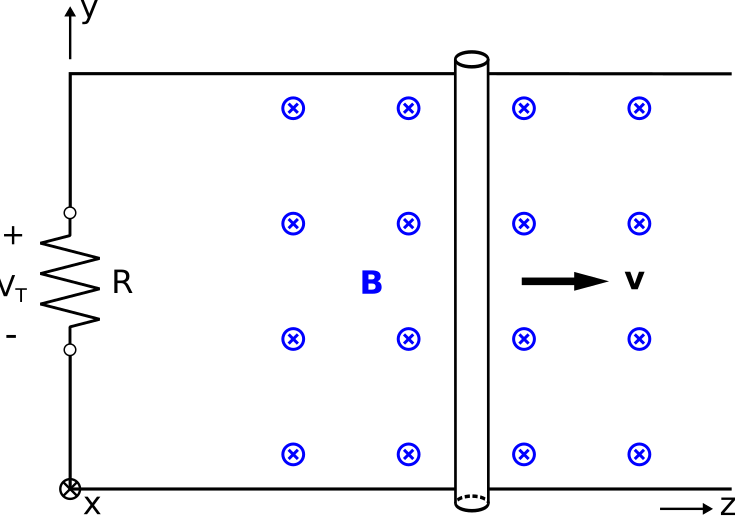
Ahora, hemos creado un bucle cerrado utilizando alambre perfectamente conductor e inmóvil para formar tres lados de un rectángulo, y asignado el origen a la esquina inferior izquierda. Se ha insertado un espacio infinitamente pequeño en el lado izquierdo (\(z=0\)) del bucle y se ha cerrado con una resistencia ideal de valor\(R\). Como antes,\({\bf B}=\hat{\bf x}B\) (espacialmente uniforme e invariante en el tiempo) y\({\bf v}=\hat{\bf z}v\) (constante). ¿Cuál es el voltaje\(V_T\) a través de la resistencia y cuál es la corriente en el bucle?
Solución
Dado que el espacio que contiene la resistencia es infinitesimalmente pequeño,
\[V_T = \oint_{\mathcal C} \left[ {\bf v} \times {\bf B} \right] \cdot d{\bf l} \nonumber \]
donde\(\mathcal{C}\) está el perímetro formado por el bucle, comenzando en el “\(-\)” terminal de\(V_T\) y regresando al “\(+\)” terminal de\(V_T\). Sólo la barra de cortocircuito está en movimiento, así que\({\bf v}=0\) para los otros tres lados del bucle. Por lo tanto, solo la porción de\(\mathcal{C}\) atravesar la barra de cortocircuito contribuye a\(V_T\). Así, encontramos
\[V_T = \int_{y=0}^{l} \left[ \hat{\bf z}v \times \hat{\bf x}B \right] \cdot \hat{\bf y}dy = Bvl \nonumber \]
Este potencial da lugar a una corriente\(Bvl/R\), que fluye en sentido contrario a las agujas del reloj.
Obsérvese en el ejemplo anterior que el campo magnético ha inducido\(V_T\), no la corriente. La corriente es simplemente una respuesta a la existencia del potencial, independientemente de la fuente. En otras palabras,\(V_T\) existiría el mismo potencial aunque la brecha no estuviera cerrada por una resistencia.
Los lectores astutos notarán que este análisis parece tener mucho en común con la ley de Faraday,
\[V = -\frac{\partial}{\partial t}\Phi \nonumber \]
que dice que el potencial inducido en un solo bucle cerrado es proporcional a la tasa temporal de cambio del flujo magnético\(\Phi\), donde
\[\Phi = \int_{S} {\bf B} \cdot d{\bf s} \nonumber \]
y dónde\(\mathcal{S}\) está la superficie a través de la cual se calcula el flujo. Desde esta perspectiva, vemos que la Ecuación\ ref {M0059_EVABC} es simplemente un caso especial de la ley de Faraday, perteneciente específicamente a la “emf mocional”. Así, el ejemplo anterior también puede ser resuelto por la ley de Faraday, tomando\(\mathcal{S}\) como superficie variable en el tiempo delimitada por\(\mathcal{C}\).


