2.4: La Ley Biot-Savart
- Page ID
- 83761
La ley Biot-Savart (BSL) proporciona un método para calcular el campo magnético debido a cualquier distribución de corriente constante (CC). En la magnetostática, la solución general a este problema emplea la ley de Ampere; es decir,
\[\int_{\mathcal C} {\bf H} \cdot d{\bf l} = I_{encl} \nonumber \]
en forma integral o
\[\nabla \times {\bf H} = {\bf J} \nonumber \]
en forma diferencial. La forma integral es relativamente simple cuando el problema presenta un alto grado de simetría, facilitando una descripción simple en un sistema de coordenadas particular. Un ejemplo es el campo magnético debido a un filamento de corriente recto e infinitamente largo, que se determina fácilmente resolviendo la ecuación integral en coordenadas cilíndricas. Sin embargo, muchos problemas de interés práctico no presentan la simetría necesaria. Un ejemplo comúnmente encontrado es el campo magnético debido a un solo bucle de corriente, que se abordará en Ejemplo\(\PageIndex{1}\). Para tales problemas, se necesita la forma diferencial de la ley de Ampere.
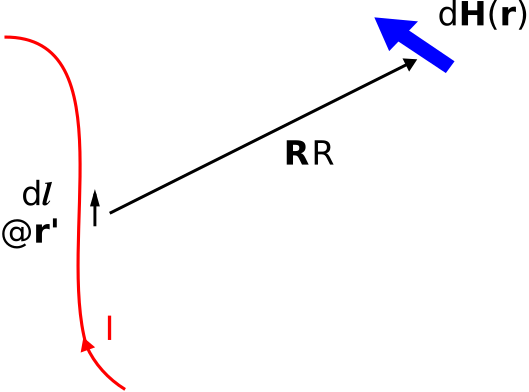
BSL es la solución a la forma diferencial de la ley de Ampere para un elemento de corriente de longitud diferencial, ilustrado en la Figura\(\PageIndex{1}\). El elemento actual es\(I~d{\bf l}\), donde\(I\) está la magnitud de la corriente (SI unidades base de A) y\(d{\bf l}\) es un vector de longitud diferencial que indica la dirección de la corriente en el “punto fuente”\({\bf r}'\). La contribución resultante a la intensidad del campo magnético en el “punto de campo”\({\bf r}\) es
\[\boxed{ d{\bf H}({\bf r}) = I~d{\bf l}~\frac{1}{4\pi R^2} \times \hat{\bf R} } \label{m0066_eBS} \]
donde
\[{\bf R} = \hat{\bf R}R \triangleq {\bf r} - {\bf r}' \nonumber \]
En otras palabras,\({\bf R}\) es el vector apuntando desde el punto de origen al punto de campo, y\(d{\bf H}\) en el punto de campo viene dado por la Ecuación\ ref {M0066_EBS}. El campo magnético debido a un cable portador de corriente de cualquier forma se puede obtener integrando sobre la longitud del cable:
\[{\bf H}({\bf r}) = \int_{\mathcal{C}} d{\bf H}({\bf r}) = \frac{I}{4\pi} \int_{\mathcal{C}} \frac{d{\bf l}\times \hat{\bf R}}{R^2} \label{m0066_eBSI} \]
Además de obviar la necesidad de resolver una ecuación diferencial, BSL proporciona información útil sobre el comportamiento de los campos magnéticos. En particular, la Ecuación\ ref {M0066_EBS} indica que los campos magnéticos siguen la ley cuadrada inversa —es decir, la magnitud del campo magnético debido a un elemento de corriente diferencial disminuye en proporción al cuadrado inverso de distancia (\(R^{-2}\)). Además, la Ecuación\ ref {M0066_EBS} indica que la dirección del campo magnético debido a un elemento de corriente diferencial es perpendicular tanto a la dirección del flujo\(\hat{\bf l}\) de corriente como al vector\(\hat{\bf R}\) que apunta desde el punto fuente al punto de campo. Esta observación es bastante útil para anticipar la dirección de los vectores de campo magnético en problemas complejos.
Puede ser útil señalar que BSL es análogo a la ley de Coulomb para campos eléctricos, que es una solución a la forma diferencial de la ley de Gauss,\(\nabla \cdot {\bf D} = \rho_v\). Sin embargo, BSL se aplica solo bajo condiciones magnetostáticas. Si la variación en las corrientes o campos magnéticos a lo largo del tiempo es significativa, entonces el problema se vuelve significativamente más complicado. Consulte “Ecuaciones de Jefimenko” en “Lectura adicional” para más información.
Considera un anillo de radio\(a\) en el\(z=0\) plano, centrado en el origen, como se muestra en la Figura\(\PageIndex{2}\).
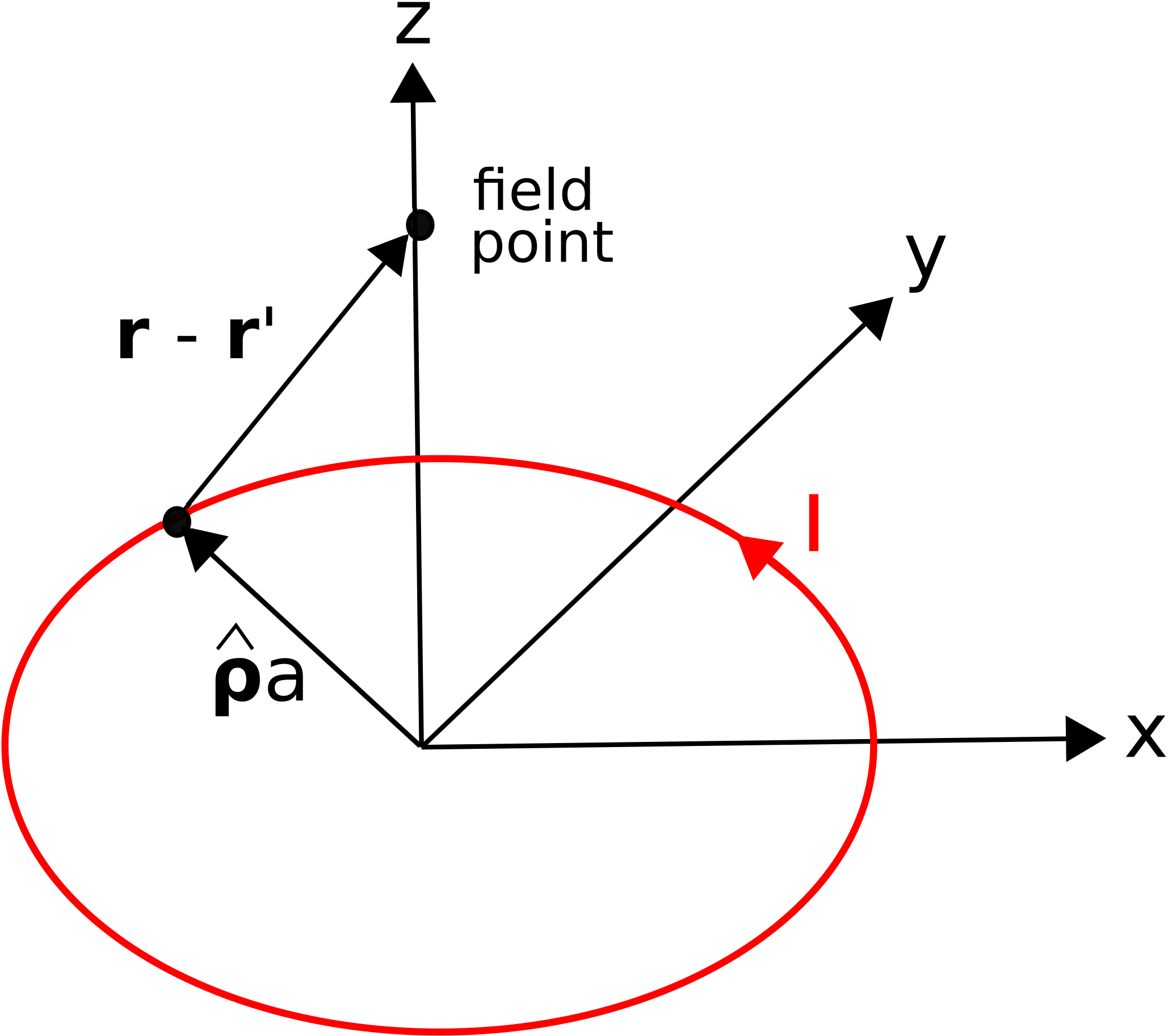
Como se indica en la figura, la corriente\(I\) fluye en la\(\hat{\bf \phi}\) dirección. Encuentra la intensidad del campo magnético a lo largo del\(z\) eje.
Solución
La posición de la corriente de origen se da en coordenadas cilíndricas como
\[{\bf r}' = \hat{\bf \rho}a \nonumber \]
La posición de un punto de campo a lo largo del\(z\) eje es
\[{\bf r} = \hat{\bf z}z \nonumber \]
Por lo tanto,
\[\hat{\bf R}R \triangleq {\bf r}-{\bf r}' = -\hat{\bf \rho}a + \hat{\bf z}z \nonumber \]
y
\[R \triangleq \left|{\bf r}-{\bf r}'\right| = \sqrt{a^2+z^2} \nonumber \]
La ecuación\ ref {M0066_EBS} se convierte en:
\[\begin{aligned} d{\bf H}(\hat{\bf z}z) &= \frac{I~\hat{\bf\phi}~ad\phi}{4\pi \left[a^2+z^2\right]} \times \frac{\hat{\bf z}z-\hat{\bf \rho}a}{\sqrt{a^2+z^2}} \nonumber \\ &= \frac{Ia}{4\pi} ~ \frac{ \hat{\bf z}a-\hat{\bf \rho}z }{\left[a^2+z^2\right]^{3/2}} ~ d\phi\end{aligned} \nonumber \]
Ahora integrándose sobre la corriente:
\[\begin{aligned} &{\bf H}(\hat{\bf z}z) = \int_{0}^{2\pi} { \frac{Ia}{4\pi} ~ \frac{ \hat{\bf z}a - \hat{\bf \rho}z }{\left[a^2+z^2\right]^{3/2}} ~ d\phi }& \end{aligned} \nonumber \]
\[\begin{aligned} &= \frac{Ia}{4\pi \left[a^2+z^2\right]^{3/2}} \int_{0}^{2\pi} { \left( \hat{\bf z}a - \hat{\bf \rho}z \right) ~ d\phi }& \end{aligned} \nonumber \]
\[\begin{aligned} &= \frac{Ia}{4\pi \left[a^2+z^2\right]^{3/2}} \left( \hat{\bf z}a \int_{0}^{2\pi} { d\phi } -z \int_{0}^{2\pi} { \hat{\bf \rho} ~ d\phi }\right)&\end{aligned} \nonumber \]
La segunda integral es igual a cero. Para ver esto, tenga en cuenta que la integral es simplemente sumando valores de\(\hat{\bf\rho}\) para todos los valores posibles de\(\phi\). Ya que\(\hat{\bf\rho}(\phi+\pi)=-\hat{\bf\rho}(\phi)\), el integrando para cualquier valor dado de\(\phi\) es igual y opuesto a los\(\pi\) radianes integrando posteriormente. (Este es un ejemplo de un argumento de simetría.)
La primera integral en la ecuación anterior es igual a\(2\pi\). Así, obtenemos
\[{\bf H}(\hat{\bf z}z) = \hat{\bf z}\frac{I a^2}{2\left[a^2+z^2\right]^{3/2}} \nonumber \]
Tenga en cuenta que el resultado es consistente con la “regla de la mano derecha” asociada de la magnetostática: Es decir, la dirección del campo magnético está en la dirección de los dedos curvados de la mano derecha cuando el pulgar de la mano derecha está alineado con la ubicación y dirección de la corriente. Es un buen ejercicio para confirmar que este resultado también es dimensionalmente correcto.
La ecuación\ ref {M0066_EBS} se extiende directamente a otras distribuciones de corriente. Por ejemplo, el campo magnético debido a la corriente superficial\({\bf J}_s\) (unidades base SI de A/m) se puede calcular usando la ecuación\ ref {M0066_Ebs} con\(I~d{\bf l}\) reemplazado por
\[{\bf J}_s~ds \nonumber \]
donde\(ds\) es el elemento diferencial del área de superficie. Esto se puede confirmar mediante análisis dimensional:\(I~d{\bf l}\) tiene unidades base SI de A\(\cdot\) m, al igual que lo hace\({\bf J}_S~ds\). Del mismo modo, el campo magnético debido a la corriente de volumen\({\bf J}\) (unidades base SI de A/m\(^2\)) se puede calcular usando la Ecuación\ ref {M0066_EBS} con\(I~d{\bf l}\) reemplazado por
\[{\bf J}~dv \nonumber \]
donde\(dv\) está el elemento diferencial de volumen. Para una sola partícula con carga\(q\) (unidades base SI de C) y velocidad\({\bf v}\) (unidades base SI de m/s), la cantidad relevante es
\[q{\bf v} \nonumber \]
ya que C\(\cdot\) m/s\(=\) (C/s)\(\cdot\) m = A\(\cdot\) m. en todos estos casos, la Ecuación\ ref {M0066_EBS} aplica con el reemplazo apropiado para\(I~d{\bf l}\).
Tenga en cuenta que las cantidades\(q{\bf v}\)\(I~d{\bf l}\)\({\bf J}_S~ds\),,\({\bf J}~dv\), y, teniendo todas las mismas unidades de A\(\cdot\) m, parecen estar refiriéndose a la misma cantidad física. Esta cantidad física se conoce como momento actual. Así, la “entrada” a BSL puede interpretarse como momento actual, independientemente de que la corriente de interés se distribuya como una corriente de línea, una corriente superficial, una corriente volumétrica o simplemente como partículas cargadas en movimiento. Consulte “Lectura adicional” al final de esta sección para obtener información adicional sobre el concepto de “momento” en la física clásica.
Lectura adicional:
- “Ley Biot-Savart” en Wikipedia.
- “Ecuaciones de Jefimenko” en Wikipedia.
- “Momento (física)” en Wikipedia.