5.8: Ángulos de reflexión y refracción
- Page ID
- 83813
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Consideremos la situación que se muestra en la Figura\(\PageIndex{1}\):
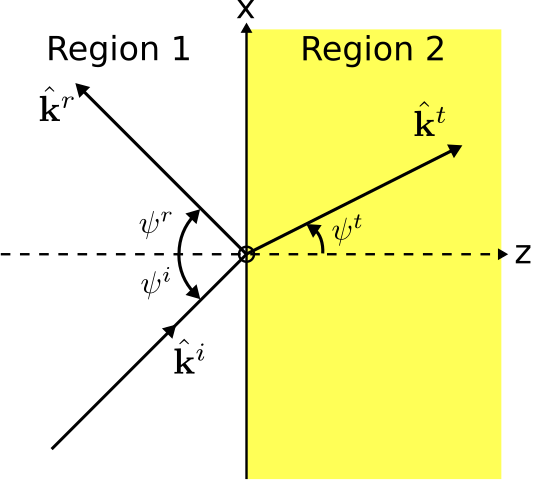
Onda plana uniforme que incide oblicuamente en el límite plano entre dos regiones de material semi-infinitas. Dejar que un punto en el límite se represente como el vector de posición
\[{\bf r}_0 = \hat{\bf x}x + \hat{\bf y}y \nonumber \]
En ambas Secciones 5.6 (“Ondas Planas a Incidencia Oblicua en un Límite Plano: Caso TE”) y 5.7 (“Ondas Planas a Incidencia Oblicua en un Límite Plano: Caso TM”), se encuentra que
\[{\bf k}^i\cdot{\bf r}_0 = {\bf k}^r\cdot{\bf r}_0 = {\bf k}^t\cdot{\bf r}_0 \label{m0168_eSL} \]
En esta expresión,
\[\begin{aligned} {\bf k}^i &= \beta_1 \hat{\bf k}^i \\ {\bf k}^r &= \beta_1 \hat{\bf k}^r \\ {\bf k}^t &= \beta_2 \hat{\bf k}^t \end{aligned} \nonumber \]
donde\(\hat{\bf k}^i\)\(\hat{\bf k}^r\), y\(\hat{\bf k}^t\) son vectores unitarios en la dirección de incidencia, reflexión y transmisión, respectivamente;\(\beta_1\) y\(\beta_2\) son las constantes de propagación de fase en la Región 1 (a partir de la cual incide la onda) y la Región 2, respectivamente. La ecuación\ ref {m0168_ESL} es esencialmente una condición límite que obliga a la continuidad de la fase de los campos eléctricos y magnéticos a través del límite, y a veces se conoce como el requisito de “coincidencia de fase”. Dado que el mismo requisito surge independientemente en los casos TE y TM, y dado que cualquier onda plana puede descomponerse en componentes TE y TM, el requisito debe aplicarse a cualquier onda plana incidente independientemente de la polarización.
La ecuación\ ref {M0168_ESL} es la clave para encontrar la dirección de reflexión\(\psi^r\) y dirección de transmisión\(\psi^t\). Primero, observe:
\[\begin{align} \hat{\bf k}^i &= \hat{\bf x}\sin\psi^i + \hat{\bf z}\cos\psi^i \\ \hat{\bf k}^r &= \hat{\bf x}\sin\psi^r - \hat{\bf z}\cos\psi^r \\ \hat{\bf k}^t &= \hat{\bf x}\sin\psi^t + \hat{\bf z}\cos\psi^t \end{align} \nonumber \]
Por lo tanto, podemos expresar la Ecuación\ ref {M0168_ESL} en la siguiente forma
\[\begin{align} \beta_1\left(\hat{\bf x}\sin\psi^i + \hat{\bf z}\cos\psi^i\right)\cdot\left(\hat{\bf x}x + \hat{\bf y}y\right) \nonumber \\ =\beta_1\left(\hat{\bf x}\sin\psi^r - \hat{\bf z}\cos\psi^r\right)\cdot\left(\hat{\bf x}x + \hat{\bf y}y\right) \nonumber \\ =\beta_2\left(\hat{\bf x}\sin\psi^t + \hat{\bf z}\cos\psi^t\right)\cdot\left(\hat{\bf x}x + \hat{\bf y}y\right) \end{align} \nonumber \]
lo que reduce a
\[\beta_1 \sin\psi^i =\beta_1 \sin\psi^r =\beta_2 \sin\psi^t \label{m0168_eA3} \]
Examinando los términos primero y segundo de la Ecuación\ ref {M0168_Ea3},\(\psi^i\) y señalando que y ambos\(\psi^r\) están limitados al rango\(-\pi/2\) a\(+\pi/2\), encontramos que:
\[\boxed{ \psi^r = \psi^i } \nonumber \]
En inglés sencillo:
El ángulo de reflexión es igual al ángulo de incidencia.
Examinando los términos primero y tercero de la Ecuación\ ref {M0168_Ea3}, encontramos que
\[\beta_1 \sin\psi^i = \beta_2 \sin\psi^t \label{m0168_eASL} \]
Desde\(\beta_1=\omega\sqrt{\mu_1\epsilon_1}\) y\(\beta_2=\omega\sqrt{\mu_2\epsilon_2}\), Ecuación\ ref {m0168_EASL} expresada explícitamente en términos de los parámetros constitutivos es:
\[\sqrt{\mu_1\epsilon_1} \sin\psi^i = \sqrt{\mu_2\epsilon_2} \sin\psi^t \label{m0168_eAt2} \]
Así, vemos que\(\psi^t\) no depende de la frecuencia, salvo en la medida en que los parámetros constitutivos pudieran hacerlo. También podemos expresar esta relación en términos de los valores relativos de los parámetros constitutivos; es decir,\(\mu_1=\mu_{r1}\mu_0\),\(\epsilon_1=\epsilon_{r1}\epsilon_0\),\(\mu_2=\mu_{r2}\mu_0\), y\(\epsilon_2=\epsilon_{r2}\epsilon_0\). En términos de los parámetros relativos:
\[\boxed{ \sqrt{\mu_{r1}\epsilon_{r1}} \sin\psi^i = \sqrt{\mu_{r2}\epsilon_{r2}} \sin\psi^t } \label{m0168_eAt3} \]
Esto se conoce como la ley de Snell o la ley de la refracción. La refracción es simplemente transmisión con el resultado de que se cambia la dirección de propagación.
La ley de Snell (Ecuación\ ref {M0168_EAT3}) determina el ángulo de refracción (transmisión).
La fórmula asociada para\(\psi^t\) explícitamente es:
\[\psi^t = \arcsin\left(\sqrt{\frac{\mu_{r1}\epsilon_{r1}}{\mu_{r2}\epsilon_{r2}}} \sin\psi^i \right) \label{m0168_eAt} \]
Para el caso especial común de los medios no magnéticos, se supone\(\mu_{r1}=\mu_{r2}= 1\). En este caso, la ley de Snell simplifica para:
\[\sqrt{\epsilon_{r1}} \sin\psi^i = \sqrt{\epsilon_{r2}} \sin\psi^t \label{m0168_eAtnm} \]
En óptica, es común expresar permitividades en términos de índices de refracción; e.g.,\(n_1\triangleq\sqrt{\epsilon_{r1}}\) y\(n_2\triangleq\sqrt{\epsilon_{r2}}\). Así, la ley de Snell en óptica a menudo se expresa como:
\[n_1 \sin\psi^i = n_2 \sin\psi^t \label{m0168_eAtnmo} \]
Cuando ambos medios son no magnéticos, la ecuación\ ref {M0168_Eat} simplifica a
\[\psi^{t}=\arcsin \left( \sqrt{\frac{\epsilon_{\mathrm{r} 1}}{\epsilon_{r 2}}} \sin \psi^{i} \right) \nonumber \]
Cuando\(\epsilon_{r2}>\epsilon_{r1}\), observamos eso\(\psi^t < \psi^i\). En otras palabras, la onda transmitida viaja en una dirección que está más cerca de la superficie normal que el ángulo de incidencia. Este escenario se demuestra en el siguiente ejemplo.
La figura\(\PageIndex{2}\) muestra un haz de luz estrecho que incide del aire al vidrio en ángulo\(\psi^i=60^{\circ}\).

Como era de esperar,\(\psi^r\) se observa que el ángulo de reflexión es igual a\(\psi^i\). Se observa que el ángulo de refracción\(\psi^t\) es\(35^{\circ}\). ¿Cuál es la permitividad relativa del vidrio?
Solución
Dado que la permitividad del vidrio es mayor que la del aire, observamos el resultado esperado\(\psi^t<\psi^i\). Dado que el vidrio no es magnético, la relación esperada entre estos ángulos viene dada por la Ecuación\ ref {M0168_EATnm}. Resolviendo esa ecuación para la permitividad relativa del vidrio, obtenemos:
\[\epsilon_{r2} = \epsilon_{r1} \left(\frac{\sin\psi^i}{\sin\psi^t}\right)^2 \cong \underline{2.28} \nonumber \]
Cuando una onda viaja en la dirección inversa —es decir, de un medio no magnético de mayor permitividad a un medio de menor permitividad— se encuentra\(\psi^t>\psi^r\). En otras palabras, la refracción está alejada de la superficie normal. La figura\(\PageIndex{3}\) muestra un ejemplo a partir de la experiencia común.
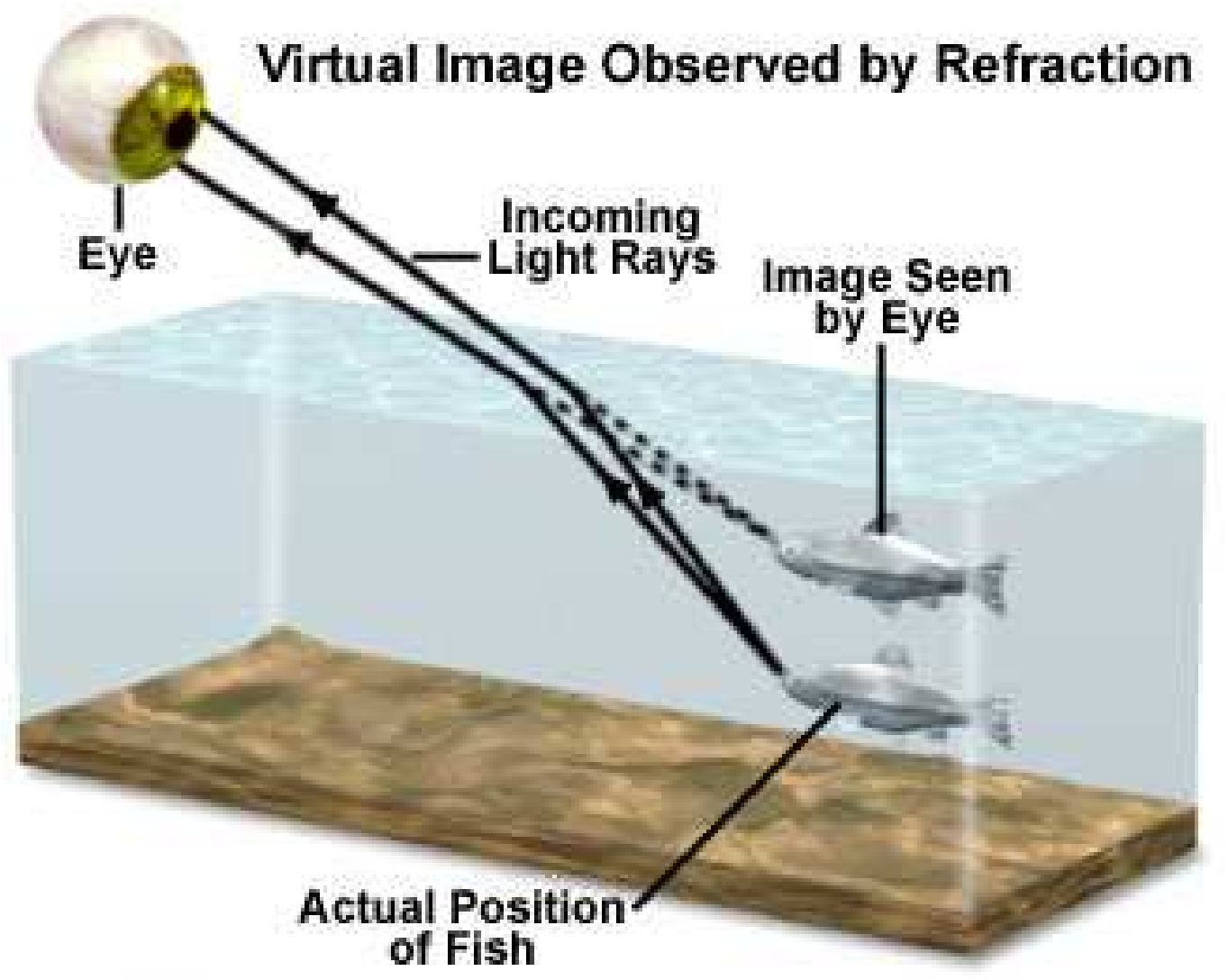
En medios no magnéticos, cuando\(\epsilon_{r1}<\epsilon_{r2}\),\(\psi_t<\psi_i\) (refracción hacia la superficie normal). Cuando\(\epsilon_{r1}>\epsilon_{r2}\),\(\psi_t>\psi_i\) (refracción lejos de la superficie normal).
Bajo ciertas condiciones, el\(\epsilon_{r2}<\epsilon_{r1}\) caso lleva a la siguiente observación sorprendente: Al calcular\(\psi^t\) usando, por ejemplo, la Ecuación\ ref {M0168_Eat}, se encuentra que\(\sqrt{\epsilon_{r1}/\epsilon_{r2}} \sin\psi^i\) puede ser mayor que 1. Dado que la\(\sin\) función produce valores entre\(-1\) y\(+1\), el resultado de la\(\arcsin\) función es indefinido. Esta extraña situación se aborda en la Sección 5.11. Por ahora, simplemente notaremos que esta condición conduce al fenómeno de la reflexión interna total. Por ahora, lo único que podemos decir es que cuando\(\epsilon_{r2}<\epsilon_{r1}\),\(\psi^t\) es capaz de alcanzar\(\pi/2\) radianes, lo que corresponde a la propagación paralela al límite. Más allá de ese umbral, debemos dar cuenta de las consideraciones físicas únicas asociadas a la reflexión interna total.
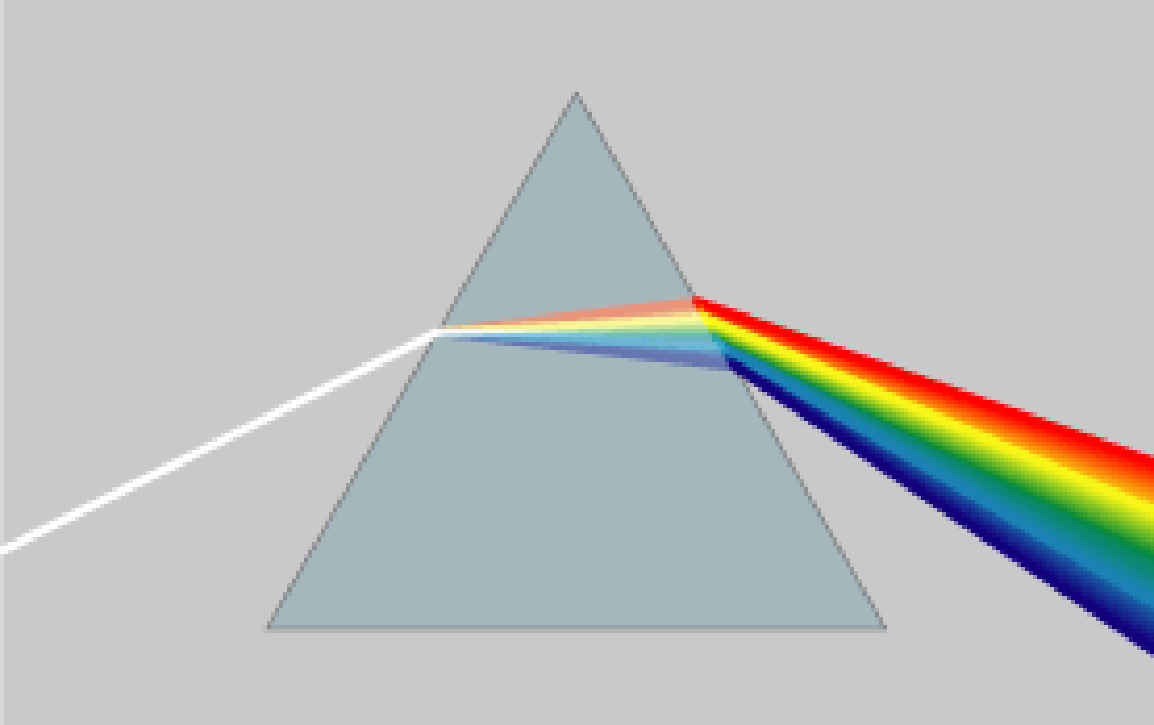
Concluimos esta sección con una descripción del dispositivo común de guía de ondas conocido como prisma, mostrado en la Figura\(\PageIndex{4}\). Este dispositivo en particular usa la refracción para cambiar la dirección de las ondas de luz (dispositivos similares también se pueden usar para manipular ondas de radio).

Muchos lectores están familiarizados con el uso de prismas para separar la luz blanca en sus colores constituyentes (frecuencias), como se muestra en la Figura\(\PageIndex{5}\). La separación de colores se debe a la dependencia de la frecuencia del material que comprende el prisma. Específicamente, la permitividad del material es una función de la frecuencia, y por lo tanto el ángulo de refracción es una función de la frecuencia. Así, cada frecuencia es refractada en una cantidad diferente. Por el contrario, un prisma compuesto por un material cuya permitividad exhibe una variación insignificante con la frecuencia no separará la luz blanca incidente en sus colores constituyentes ya que cada color será refractado en la misma cantidad.