6.5: Guía de ondas de placa paralela - Caja TM, campo eléctrico
- Page ID
- 83717
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)En la Sección 6.2 se introdujo la guía de ondas de placa paralela mostrada en\(\PageIndex{1}\) la Figura.
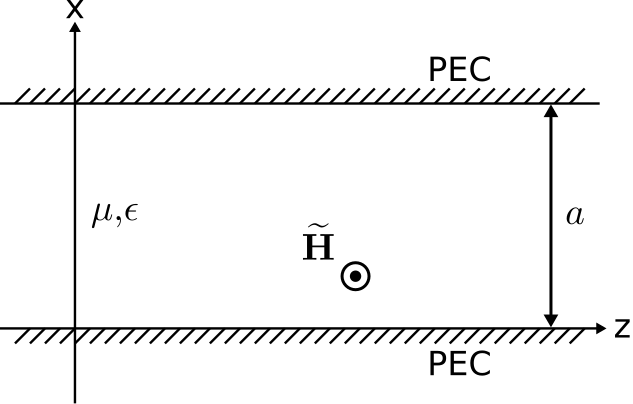
Al final de esa sección, descompusimos el problema en sus componentes TE y TM. En esta sección, encontramos el componente TM de los campos en la guía de ondas.
“" "Magnético transversal "” significa que el vector de campo magnético es perpendicular al plano de interés y, por lo tanto, es paralelo a las superficies conductoras.” Así,\(\widetilde{\bf H} = \hat{\bf y}\widetilde{H}_y\), sin componente en las\(\hat{\bf z}\) direcciones\(\hat{\bf x}\) o. Siguiendo precisamente el mismo razonamiento empleado en la Sección 6.2, encontramos que la ecuación gobernante para el componente magnético del campo TM es:
\[\frac{\partial^2}{\partial x^2}\widetilde{H}_y + \frac{\partial^2}{\partial z^2}\widetilde{H}_y = - \beta^2 \widetilde{H}_y \label{m0177_eDH} \]
La solución general a esta ecuación diferencial parcial es:
\[\begin{align} \widetilde{H}_y =&~~~~~e^{-jk_z z} \left[ A e^{-jk_x x} + B e^{+jk_x x} \right] \nonumber \\ &+e^{+jk_z z} \left[ C e^{-jk_x x} + D e^{+jk_x x} \right] \label{m0177_eGS}\end{align} \]
donde\(A\),\(B\)\(C\), y\(D\) son constantes de valor complejo; y\(k_x\) y\(k_z\) son constantes de valor real. Hemos asignado nombres de variables a estas constantes con conocimiento avanzado de su interpretación física; sin embargo, en este momento siguen siendo constantes simplemente desconocidas cuyos valores deben ser determinados por la aplicación de condiciones límite.
Tenga en cuenta que la Ecuación\ ref {M0177_EGS} consta de dos términos. El primer término incluye el factor\(e^{-jk_z z}\), indicando una onda que se propaga en la\(+\hat{\bf z}\) dirección, y el segundo término incluye el factor\(e^{+jk_z z}\), indicando una onda que se propaga en la\(-\hat{\bf z}\) dirección. Si imponemos la restricción de que las fuentes existen solo en el lado izquierdo (\(z<0\)) de la Figura\(\PageIndex{1}\), y que no hay ninguna estructura capaz de dispersar ondas (en particular, reflexión) en el lado derecho (\(z>0\)) de la Figura\(\PageIndex{1}\), entonces no puede haber componentes de onda que se propaguen en el \(-\hat{\bf z}\)dirección. En este caso,\(C=D=0\) y la Ecuación\ ref {M0177_EGS} simplifica a:
\[\widetilde{H}_y = e^{-jk_z z} \left[ A e^{-jk_x x} + B e^{+jk_x x} \right] \label{m0177_eGS2} \]
Antes de continuar, asegurémonos de que la Ecuación\ ref {M0177_EGS2} es en realidad una solución a la Ecuación\ ref {M0177_EDH}. Como en el caso TE, esta comprobación produce una restricción (de hecho, la misma restricción) sobre los parámetros aún indeterminados\(k_x\) y\(k_z\). Primero, tenga en cuenta:
\[\frac{\partial \widetilde{H}_y}{\partial x} = e^{-jk_z z} \left[-A e^{-jk_x x} + B e^{+jk_x x} \right]\left(jk_x\right) \label{m0177_edHydx} \]
Entonces:
\[\begin{align} \frac{\partial^2 \widetilde{H}_y}{\partial x^2} &= e^{-jk_z z} \left[ A e^{-jk_x x} + B e^{+jk_x x} \right]\left(-k_x^2\right) \nonumber \\ &= -k_x^2 \widetilde{H}_y\end{align} \nonumber \]
Siguiente, tenga en cuenta:
\[\frac{\partial \widetilde{H}_y}{\partial z} = e^{-jk_z z} \left[ A e^{-jk_x x} + B e^{+jk_x x} \right]\left(-jk_z\right) \label{m0177_edHydz} \]
Entonces:
\[\begin{align} \frac{\partial^2 \widetilde{H}_y}{\partial z^2} &= e^{-jk_z z} \left[ A e^{-jk_x x} + B e^{+jk_x x} \right]\left(-k_z^2\right) \nonumber \\ &= -k_z^2 \widetilde{H}_y\end{align} \nonumber \]
Ahora sumando estos resultados:
\[\frac{\partial^2 \widetilde{H}_y}{\partial x^2} + \frac{\partial^2 \widetilde{H}_y}{\partial z^2} = -\left( k_x^2 + k_z^2 \right) \widetilde{H}_y \label{m0177_eDE2} \]
Comparando la Ecuación\ ref {M0177_Ede2} con la Ecuación\ ref {M0177_EDH}, concluimos que la Ecuación\ ref {M0177_EGS2} es una solución a la Ecuación\ ref {M0177_EDH} bajo la restricción de que:
\[\beta^2 = k_x^2 + k_z^2 \label{m0177_eBeta} \]
Esta es precisamente la misma restricción identificada en el caso TE, y confirma que\(k_x\) y\(k_y\) son de hecho los componentes del vector de propagación
\[{\bf k} \triangleq \beta\hat{\bf k} = \hat{\bf x}k_x + \hat{\bf y}k_y + \hat{\bf z}k_z \nonumber \]
dónde\(\hat{\bf k}\) está el vector unitario apuntando en la dirección de propagación, y\(k_y=0\) en este problema particular.
Nuestro objetivo en esta sección es determinar el componente del campo eléctrico del campo TM. El campo eléctrico puede obtenerse del campo magnético utilizando la ley de Ampere:
\[\nabla \times \widetilde{\bf H} = j\omega\epsilon \widetilde{\bf E} \nonumber \]
Así:
\[\begin{align} \widetilde{\bf E} &= \frac{1}{j\omega\epsilon}~\nabla \times \widetilde{\bf H} \nonumber \\ &= \frac{1}{j\omega\epsilon}~\nabla \times \left(\hat{\bf y}\widetilde{H}_y\right) \end{align} \nonumber \]
La forma relevante del operador de rizo es
\ begin {alineado}
\ nabla\ times\ mathbf {A} =&\ hat {\ mathbf {x}}\ left (\ frac {\ parcial A_ {z}} {\ parcial y} -\ frac {\ parcial A_ {y}} {\ parcial z}\ derecha)\\
&+\ hat {\ mathbf {y}}\ izquierda (\ frac {\ parcial A_ {x}} {\ z parcial} -\ frac {\ parcial A_ {z}} {\ x parcial}\ derecha)\\
&+\ sombrero {\ mathbf {z}}\ izquierda (\ frac {\ parcial A_ {y}} {\ parcial x} -\ frac {\ parcial A_ {x}} {\ parcial y}\ derecha)
\ final {alineado}
del Apéndice 12.2. Aunque la expresión completa consta de 6 términos, todos menos 2 de estos términos son cero porque los\(\hat{\bf z}\) componentes\(\hat{\bf x}\) y de\(\widetilde{\bf H}\) son cero. Los dos términos restantes son\(-\hat{\bf x}\partial \widetilde{H}_y/\partial z\) y\(+\hat{\bf z}\partial \widetilde{H}_y/\partial x\). Así:
\[\widetilde{\bf E} = \frac{1}{j\omega\epsilon}~\left( -\hat{\bf x}\frac{\partial\widetilde{H}_y}{\partial z} +\hat{\bf z}\frac{\partial\widetilde{H}_y}{\partial x} \right) \label{m0177_eE} \]
Podemos desarrollar aún más esta expresión usando las Ecuaciones\ ref {M0177_EdhydX} y\ ref {M0177_EdhydZ}. Encontramos que el\(\hat{\bf x}\) componente de\(\widetilde{\bf E}\) es:
\[\widetilde{E}_x = \frac{k_z}{\omega\epsilon}~e^{-jk_z z} \left[ A e^{-jk_x x} + B e^{+jk_x x} \right] \label{m0177_eEx} \]
y el\(\hat{\bf z}\) componente de\(\widetilde{\bf E}\) es:
\[\widetilde{E}_z = \frac{k_x}{\omega\epsilon}~e^{-jk_z z} \left[ -A e^{-jk_x x} + B e^{+jk_x x} \right] \label{m0177_eEz} \]
La solución ahora se ha reducido al problema de encontrar las constantes\(A\),\(B\), y ya sea\(k_x\) o\(k_z\). Esto se logra mediante el cumplimiento de las condiciones de frontera relevantes. En general, el componente del campo eléctrico que es tangente a una superficie perfectamente conductora es cero. Aplicado al presente (TM) caso, esto significa\(\widetilde{E}_z\left(x=0\right) = 0\) y\(\widetilde{E}_z\left(x=a\right) = 0\). Refiriéndose a la Ecuación\ ref {M0177_EEZ}, la condición de límite en\(x=0\) medias
\[\frac{k_x}{\omega\epsilon}~e^{-jk_z z} \left[ -A \left(1\right) + B \left(1\right) \right] = 0 \nonumber \]
El factor\(e^{-jk_z z}\) siempre tiene magnitud unitaria, y así no puede ser cero. Podríamos requerir\(k_x\) ser cero, pero esto es innecesariamente restrictivo. En su lugar, requerimos\(A=B\) y podemos reescribir la ecuación\ ref {m0177_eez} de la siguiente manera:
\[\widetilde{E}_z = \frac{B k_x}{\omega\epsilon}~e^{-jk_z z} \left[ e^{+jk_x x} - e^{-jk_x x} \right] \nonumber \]
Esta expresión se simplifica usando una identidad trigonométrica:
\[\sin{k_x a} = \frac{1}{2j}\left[ e^{+jk_x a} - e^{-jk_x a} \right] \nonumber \]
Así:
\[\widetilde{E}_z = \frac{j2B k_x}{\omega\epsilon} e^{-jk_z z} \sin k_x x \nonumber \]
Ahora siguiendo con\(\widetilde{E}_x\), comenzando desde la ecuación\ ref {M0177_Eex}:
\[\begin{align} \widetilde{E}_x &= \frac{k_z}{\omega\epsilon}~e^{-jk_z z} \left[ A e^{-jk_x x} + B e^{+jk_x x} \right] \nonumber \\ &= \frac{B k_z}{\omega\epsilon}~e^{-jk_z z} \left[ e^{-jk_x x} + e^{+jk_x x} \right] \nonumber \\ &= \frac{2B k_z}{\omega\epsilon}~e^{-jk_z z} \cos k_x x\end{align} \nonumber \]
Por conveniencia definimos la siguiente constante de valor complejo:
\[E_{x0}\triangleq \frac{2B k_z}{\omega\epsilon} \nonumber \]
Esto produce la siguiente expresión más simple:
\[\widetilde{E}_x = E_{x0}~e^{-jk_z z} \cos k_x x \nonumber \]
Ahora apliquemos la condición de límite\(x=a\) a\(\widetilde{E}_{z}\):
\[\frac{j2B k_z}{\omega\epsilon} e^{-jk_z z} \sin k_x a = 0 \nonumber \]
Exigir\(B=0\) o\(k_z=0\) arrojar sólo soluciones triviales, por lo tanto, debe ser cierto que
\[\sin{k_x a} = 0 \nonumber \]
Esto a su vez requiere que
\[k_x a = m \pi \nonumber \]
donde\(m\) es un entero. Tenga en cuenta que esta es precisamente la misma relación que identificamos en el caso TE. Sin embargo, hay una diferencia importante. En el caso TE, no\(m=0\) fue de interés porque esto rinde\(k_x=0\), y el campo asociado resultó ser idénticamente cero. En el presente caso (TM),\(m=0\) también rinde\(k_x=0\), pero el campo asociado no es necesariamente cero. Es decir, para\(m=0\),\(\widetilde{E}_z=0\) pero no\(\widetilde{E}_x\) es necesariamente cero. Por lo tanto, así\(m=0\) como\(m=1\)\(m=2\),, y así sucesivamente son de interés en el caso TM.
En este punto, hemos descubierto una familia de soluciones con\(m=0,1,2,...\). Cada solución se conoce como un modo, y se asocia con un valor particular de\(k_x\). En la discusión que sigue, encontraremos que las consecuencias son idénticas a las identificadas en el caso TE, salvo que\(m=0\) ahora también se permite. Continuando: El valor de\(k_z\) for mode\(m\) se obtiene usando la Ecuación\ ref {M0177_Ebeta} de la siguiente manera:
\[\begin{align} k_z &= \sqrt{\beta^2-k_x^2} \nonumber \\ & =\sqrt{\beta^2-\left(\frac{m\pi}{a}\right)^2}\end{align} \nonumber \]
Dado que\(k_z\) se especifica para ser de valor real, requerimos:
\[\beta^2-\left(\frac{m\pi}{a}\right)^2 > 0 \nonumber \]
Esto limita\(\beta\); específicamente:
\[\beta > \frac{m\pi}{a} \nonumber \]
Recordemos eso\(\beta=\omega\sqrt{\mu\epsilon}\) y\(\omega=2\pi f\) dónde\(f\) está la frecuencia. Resolviendo para\(f\), encontramos:
\[f > \frac{m}{2a\sqrt{\mu\epsilon}} \nonumber \]
Así, cada modo existe solo por encima de una cierta frecuencia, que es diferente para cada modo. Esta frecuencia de corte\(f_c\) para el modo\(m\) viene dada por
\[\boxed{ f_c^{(m)} \triangleq \frac{m}{2a\sqrt{\mu\epsilon}} } \label{m0177_efcm} \]
A frecuencias por debajo de la frecuencia de corte para el modo\(m\), los modos\(0\) a través de\(m-1\) exhiben valores imaginarios\(k_z\) y por lo tanto no se propagan. Además, tenga en cuenta que la frecuencia de corte para\(m=0\) es cero, por lo que este modo siempre es capaz de propagarse. Es decir, el\(m=0\) modo puede existir para cualquiera\(a>0\) y cualquiera\(f>0\). Una vez más, esta es una diferencia notable con respecto al caso TE, para el cual no\(m=0\) está disponible.
Resumamos ahora la solución. Con respecto a la Figura\(\PageIndex{1}\), encontramos que el componente de campo eléctrico del campo TM viene dado por:
\[\boxed{ \widetilde{\bf E} = \sum_{m=0}^{\infty} \left[ \hat{\bf x} \widetilde{E}_x^{(m)} + \hat{\bf z} \widetilde{E}_z^{(m)} \right] } \label{m0177_eEsum} \]
donde
\[\boxed{ \widetilde{E}_x^{(m)} \triangleq \begin{cases} 0, & f<f_c^{(m)} \\ E_{x0}^{(m)} e^{-jk_z^{(m)} z} \cos k_x^{(m)} x, & f\ge f_c^{(m)} \end{cases} } \nonumber \]
y
\[\boxed{ \widetilde{E}_z^{(m)} \triangleq \begin{cases} 0, & f<f_c^{(m)} \\ j\frac{k_x^{(m)}}{k_z^{(m)}}E_{x0}^{(m)} e^{-jk_z^{(m)} z} \sin k_x^{(m)} x, & f\ge f_c^{(m)} \end{cases} } \nonumber \]
donde se\(m\) enumeran los modos (\(m=0,1,2,...\)) y
\[\boxed{ k_z^{(m)} \triangleq \sqrt{\beta^2-\left[k_x^{(m)}\right]^2} } \nonumber \]
\[\boxed{ k_x^{(m)} \triangleq m\pi/a } \label{m0177_ekxma} \]
Finalmente, los coeficientes\(E_{x0}^{(m)}\) dependen de fuentes y/o condiciones de límite a la izquierda de la región de interés.
Para el escenario representado en la Figura\(\PageIndex{1}\), el componente de campo eléctrico de la solución TM viene dado por la Ecuación\ ref {M0177_eesum} con componentes modales determinados como se indica por Ecuaciones\ ref {m0177_efcm} -\ ref {m0177_ekxma}. Esta solución presume que todas las fuentes se encuentran a la izquierda de la región de interés, sin fuentes adicionales ni condiciones límite a la derecha de la región de interés.
El\(m=0\) modo, comúnmente denominado modo “TM\(_0\)”, es de particular importancia en el análisis de la línea de transmisión de microcinta, y se aborda en la Sección 6.6.


