6.6: Guía de ondas de placa paralela: el modo TM0
- Page ID
- 83712
En la Sección 6.2, se introdujo la guía de ondas de placa paralela (también mostrada en la Figura\(\PageIndex{1}\)).
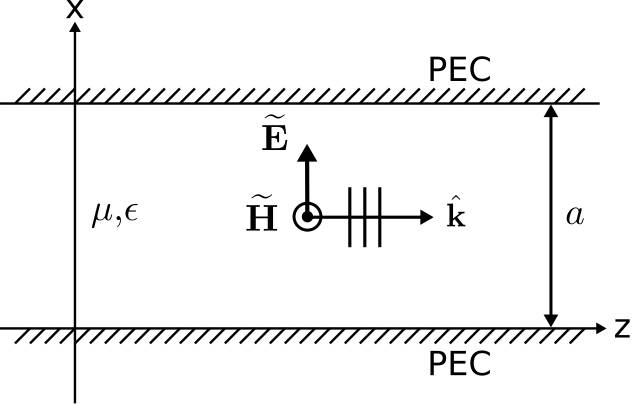
Al final de esa sección descompusimos el problema en sus campos constitutivos TE y TM. En la Sección 6.5, se determinó el componente de campo eléctrico del campo TM, el cual se encontró que consistía en un conjunto de modos discretos. En esta sección, abordamos el modo de orden más bajo (\(m=0\)) del campo TM, que tiene especial relevancia en una serie de aplicaciones, incluidas las líneas de transmisión de microcinta. Este modo se conoce comúnmente como el modo “TM\(_0\)”.
La intensidad del campo eléctrico TM en la guía de ondas viene dada por la Ecuación 6.5.31 con componentes modales determinados como lo indican las Ecuaciones 6.5.30-6.5.35 (Sección 6.5). Recordemos que el\(m=0\) modo solo puede existir en el caso TM, y no existe en el caso TE. También notamos que la frecuencia de corte para este modo es cero, por lo que puede existir en cualquier frecuencia, y dentro de cualquier separación de placas distinta de cero\(a\). Para este modo\(k_x^{(0)} = 0\)\(k_z^{(0)}=\beta\),, y encontramos
\[\widetilde{\bf E} = \hat{\bf x} E_{x0}^{(0)} e^{-j\beta z} ~~~ \mbox{(TM$_0$ mode)} \nonumber \]
Sorprendentemente, encontramos que este modo tiene la forma de una onda plana uniforme que se propaga en la\(+\hat{\bf z}\) dirección; es decir, directamente entre las placas. Las velocidades de fase y grupo de esta onda son iguales entre sí y\(\omega/\beta\), precisamente como se esperaba para una onda plana uniforme en medios no acotados; es decir, como si las placas no existieran. Esta observación nos permite determinar fácilmente el campo magnético asociado: Usando la relación de onda plana,
\[\begin{align} \widetilde{\bf H} &= \frac{1}{\eta}\hat{\bf k} \times \widetilde{\bf E} \\ &= \frac{1}{\eta}\hat{\bf z} \times \left( \hat{\bf x} E_{x0}^{(0)} e^{-j\beta z} \right) \\ &= \hat{\bf y} \frac{E_{x0}^{(0)}}{\eta} e^{-j\beta z} ~~~ \mbox{(TM$_0$ mode)}\end{align} \nonumber \]
Una forma muy común de PCB consiste en una losa de 1.575 mm de espesor de dieléctrico de baja pérdida que tiene permitividad relativa\(\approx 4.5\) intercalada entre dos planos de cobre. Caracterizar el campo electromagnético en una tira larga de este material. Supongamos que existe una sola fuente en un extremo de la tira y opera a frecuencias por debajo de 10 GHz.
Solución
Supongamos que los planos de cobre exhiben una conductividad suficientemente alta para que las superficies orientadas hacia adentro puedan verse como perfectamente conductoras. Además, limitemos el alcance al campo en lo profundo del “sándwich”, y descuidemos la región cerca de los bordes de la PCB. En estas condiciones, la PCB está bien modelada como una guía de ondas de placa paralela. Así, el campo electromagnético consiste en una combinación de modos TE y TM. Los modos activos (distintos de cero) dependen de la fuente (un modo debe ser “estimulado” por la fuente para propagarse) y frecuencias de corte modales. La frecuencia de corte para el modo\(m\) es
\[f^{(m)}_c = \frac{m}{2a\sqrt{\mu\epsilon}} \nonumber \]
En este caso,\(a=1.575\) mm,\(\mu\approx\mu_0\), y\(\epsilon\approx 4.5\epsilon_0\). Por lo tanto:
\[f^{(m)}_c \approx \left( 44.9~\mbox{GHz} \right) m \nonumber \]
Dado que la frecuencia de corte para\(m=1\) es mucho mayor que 10 GHz, podemos estar seguros de que el único modo que puede propagarse dentro de la PCB es TM\(_0\). Por lo tanto, el campo profundo dentro de la PCB puede interpretarse como una onda plana única que tiene la\(_0\) estructura TM mostrada en la Figura\(\PageIndex{1}\), que se propaga lejos del extremo fuente de la PCB. La velocidad de fase es simplemente la de la onda plana aparente:
\[v_p = \frac{1}{\sqrt{\mu\epsilon}} \approx 1.41 \times 10^8~\mbox{m/s} \approx 0.47c \nonumber \]
El escenario descrito en este ejemplo es esencialmente una forma muy rudimentaria de línea de transmisión de microcinta.


