4.7: Procesos de Renovación-Recompensa y Promedios del Conjunto
- Page ID
- 86276
El teorema 4.4.1 mostró que si un proceso de renovación-recompensa tiene un intervalo entre renovaciones esperado\(\overline{X}\) y una recompensa inter-renovación esperada\(\mathrm{E}\left[R_{n}\right]\), entonces la recompensa promedio de tiempo es\(\mathrm{E}\left[R_{n}\right] / \overline{X}\) con probabilidad 1. En esta sección, exploramos el promedio de conjunto\(\mathrm{E}[R(t)]\),, en función del tiempo\(t\). Es fácil ver que\(\mathrm{E}[R(t)]\) normalmente cambia con\(t\), especialmente para los pequeños\(t\), pero una cuestión de mayor interés aquí es si se\(\mathrm{E}[R(t)]\) acerca a una constante como\(t \rightarrow \infty\).
En términos más concretos, si los tiempos de llegada de los autobuses a una estación de autobuses forman un proceso de renovación, entonces el tiempo de espera para el siguiente autobús, es decir, la vida residual, comenzando en el tiempo\(t\), puede representarse como una función de recompensa\(R(t)\). Nos gustaría saber si el tiempo de espera esperado depende críticamente de\(t\), dónde\(t\) está el tiempo desde que comenzó el proceso de renovación, es decir, el tiempo desde que llegó un hipotético autobús número 0. Si\(\mathrm{E}[R(t)]\) varía significativamente con\(t\), incluso como\(t \rightarrow \infty\), significa que la elección de\(t=0\) como inicio del intervalo inicial entre llegadas nunca muere como\(t \rightarrow \infty\).
El teorema de renovación de Blackwell (y el sentido común) nos dicen que existe una gran diferencia entre los tiempos aritméticos de inter-renovación y los tiempos de inter-renovación no aritméticos. Para el caso aritmético, todas las renovaciones ocurren en múltiplos del lapso\(\lambda\). Así, por ejemplo, el tiempo de espera esperado (es decir, la vida residual esperada) disminuye a la tasa 1 de cada múltiplo de\(\lambda\) al siguiente, y aumenta con un salto igual a la probabilidad de una llegada a cada múltiplo de\(\lambda\). Por esta razón, solemos considerar varias funciones de recompensa solo en múltiplos de\(\lambda\). Supondríamos, entonces, que\(\mathrm{E}[R(n \lambda)]\) se acerca a una constante como\(n \rightarrow \infty\).
Para el caso no aritmético, por otro lado, el número esperado de renovaciones en cualquier pequeño intervalo de longitud\(\delta\) se vuelve independiente de\(t\) as\(t \rightarrow \infty\), por lo que podríamos adivinar que se\(\mathrm{E}[R(t)]\) acerca a un límite as\(t \rightarrow \infty\). También se adivinaría que estos promedios asintóticos de conjunto son iguales a los promedios de tiempo apropiados de la Sección 4.4.
La conclusión de esta sección es que bajo condiciones muy amplias, las conjeturas anteriores son esencialmente correctas. Por lo tanto, el límite a partir\(t \rightarrow \infty\) de una recompensa promedio de conjunto dada generalmente se puede calcular simplemente encontrando el promedio de tiempo y viceversa. A veces los promedios de tiempo son más simples, y a veces los promedios conjuntos lo son La ventaja del enfoque conjunto-promedio es tanto la capacidad\(\mathrm{E}[R(t)]\) de encontrar valores finitos como de\(t\) comprender la tasa de convergencia al resultado asintótico.
La siguiente subsección se restringe al caso aritmético. Derivaremos la función de distribución conjunta de edad y duración para cualquier tiempo dado\(t\), y luego veremos el límite como\(t \rightarrow \infty\). Esto nos lleva a funciones de recompensa arbitrarias (como la vida residual) para el caso aritmético. No veremos específicamente las funciones de recompensa generalizadas que dependen de otros procesos, pero esta generalización es bastante similar a la de los promedios de tiempo.
El caso no aritmético se analiza en el resto de las subsecciones de esta sección. Las ideas básicas son las mismas que el caso aritmético, pero surgen una serie de sutiles problemas matemáticos limitantes. Se aconseja al lector que entienda primero el caso aritmético, ya que las cuestiones limitantes en el caso no aritmético se pueden ver dentro del contexto intuitivo del caso aritmético.
duración de los procesos aritméticos
Dejar\(\{N(t) ; t>0\}\) ser un proceso aritmético de conteo de renovación con intervalos de inter-renovación\(X_{1}, X_{2}, \ldots\) y épocas de llegada\(S_{1}, S_{2}, \ldots\), donde\(S_{n}=X_{1}+\cdots+X_{n}\). Para mantener la notación lo más despejada posible, tomamos el span para ser uno y luego escalar a una arbitraria\(\lambda\) más tarde. Así, cada uno\(X_{i}\) es un rv con valor entero positivo.
Recordemos que la edad\(Z(t)\) a cualquier dada\(t>0\) es\(Z(t)=t-S_{N(t)}\) (donde por convención\(S_{0}=0\)) y la duración\(\widetilde{X}(t)\) es\(\widetilde{X}(t)=S_{N(t)+1}(t)-S_{N(t)}\). Dado que las llegadas ocurren solo en tiempos enteros, inicialmente consideramos la edad y la duración solo en tiempos enteros también. Si se produce una llegada en tiempo entero\(t\), entonces\(S_{N(t)}=t\) y\(Z(t)=0\). También, si\(S_{1}>t\), entonces\(N(t)=0\) y\(Z(t)=t\) (es decir, la edad se toma para ser\(t\) si no ocurren llegadas hasta e incluyendo el tiempo\(t\)). Así, para entero\(t\),\(Z(t)\) es un rv con valor entero tomando valores de\([0, t]\). Ya que\(S_{N(t)+1}>t\), se deduce que\(\widetilde{X}(t)\) es un rv de valor entero satisfactorio\(\widetilde{X}(t)>Z(t)\). Dado que ambos son de valor entero,\(\widetilde{X}(t)\) deben superar\(Z(t)\) en al menos 1 (o por\(\lambda\) en el caso más general de span\(\lambda\)).
Para satisfacer\(Z(t)=i\) y\(\tilde{X}(t)=k\) para dado\(i<t\), es necesario y suficiente tener una época de llegada a\(t-i\) seguida de un intervalo de interllegada de longitud\(k\), donde\(k \geq i+1\). Para\(Z(t)=t\) y\(\widetilde{X}(t)=k\), es necesario y suficiente que\(k>t\), es decir, que la primera época inter-renovación ocurra en\(k>t\).
Dejar\(\left\{X_{n} ; n \geq 1\right\}\) ser los intervalos entre llegadas de un proceso de renovación aritmética con lapso de unidad. Entonces el PMF conjunto de la edad y duración en tiempo entero\(t \geq 1\) viene dado por
\[\mathbf{p}_{Z(t), \tilde{X}(t)}(i, k)= \begin{cases}\mathbf{p}_{X}(k) & \text { for } i=t, k>t \\ q_{t-i} \mathbf{p}_{X}(k) & \text { for } 0 \leq i<t, k>i. \\ 0 & \text { otherwise }\end{cases}\label{4.62} \]
donde\(q_{j}=\operatorname{Pr}\{\text { arrival at time } j\}\). El límite en\(t \rightarrow \infty\) cuanto a cualquier dado\(0 \leq i<k\) viene dado por
\[\lim _{\text {integer } t \rightarrow \infty} \mathrm{p}_{Z(t), \widetilde{X}(t)}(i, k)=\frac{\mathrm{p}_{X}(k)}{\overline{X}}.\label{4.63} \]
- Prueba
-
La idea es bastante sencilla. Para la parte alta de (4.62), tenga en cuenta que la edad es\(t\) si y sólo no hay llegadas en\((0, t]\), lo que corresponde a\(X_{1}=k\) para algunos\(k>t\). Para la parte media, la edad es\(i\) para un dado\(i<t\) si y sólo si hay una llegada a\(t-i\) y la siguiente época de llegada es posterior\(t\), lo que significa que el intervalo interarribo correspondiente\(k\) excede\(i\). La probabilidad de una llegada a\(t-i\), es decir\(q_{t-i}\), depende únicamente de las épocas de llegada hasta e incluyendo el tiempo\(t-i\), que debe ser independiente del tiempo de llegada posterior, conduciendo al producto en el término medio de (4.62). Para ser más precisos acerca de esta independencia, tenga en cuenta que para\(i<t\),
\[q_{t-i}=\operatorname{Pr}\{\operatorname{arrival} \operatorname{at} t-i\}=\sum_{n \geq 1} \mathrm{p}_{S_{n}}(t-i)\label{4.64} \]
Dado eso\(S_{n}=t-i\), la probabilidad que\(X_{n+1}=k\) es\(\mathrm{p}_{X}(k)\). Esto es lo mismo para todos\(n\), estableciendo (4.62).
Para cualquier fijo\(i\),\(k\) con\(i<k\), tenga en cuenta que sólo el término medio en\ ref {4.62} es relevante como\(t \rightarrow \infty\). Usando el teorema de Blackwell\ ref {4.61} para tomar el límite como\(t \rightarrow \infty\), obtenemos (4.63)
Las probabilidades en el teorema, tanto para finitas\(t\) como asintóticamente como\(t \rightarrow \infty\), se ilustran en la Figura 4.17. La forma del producto de las probabilidades en\ ref {4.62} (como se ilustra en la figura) podría llevar a uno a pensar eso\(Z(t)\) y\(\widetilde{X}(t)\) son independientes, pero esto es incorrecto debido a la restricción que\(\widetilde{X}(t)>Z(t)\). Es curioso que en el caso asintótico,\ ref {4.63} muestra que, para una duración dada\(\tilde{X}(t)=k\), es igualmente probable que la edad tenga algún valor entero de 0 a\(k-1\), es decir, para una duración dada, el intervalo entre llegadas que contiene\(t\) se distribuye uniformemente alrededor\(t\).
El PMF marginal para\(Z(t)\) se calcula a continuación utilizando (4.62).
\[\mathrm{p}_{Z(t)}(i)= \begin{cases}\mathrm{F}_{X}^{\mathrm{c}}(i) & \text { for } i=t \\ q_{t-i} \mathrm{~F}_{X}^{\mathrm{c}}(i) & \text { for } 0 \leq i<t. \\ 0 & \text { otherwise }\end{cases}\label{4.65} \]

Figura 4.17: PMF conjunto,\(\mathrm{p}_{\tilde{X}(t) Z(t)}(k, i)\) de\(\widetilde{X}(t)\) y\(Z(t)\) en una renovación aritmética en un proceso de renovación aritmética con lapso 1. En la parte a),\(t=3\) y el PMF en cada punto de muestra es producto de dos términos,\(q_{t-i}=\operatorname{Pr}\{\text { Arrival at } t-i\}\) y\(\mathrm{p}_{X}(k)\). Parte b) es el caso asintótico donde\(t \rightarrow \infty\). Aquí las probabilidades de llegada se vuelven uniformes. donde\(\mathrm{F}_{X}^{c}(i)=\mathrm{p}_{X}(i+1)+\mathrm{p}_{X}(i+2)+\cdots\). El PMF marginal para se\(\widetilde{X}(t)\) puede calcular directamente a partir de (4.62), pero se simplifica algo al reconocer que
\[q_{j}=m(j)-m(j-1).\label{4.66} \]
Sustituyendo esto en\ ref {4.62} y sumando más de edad,
\[\mathrm{p}_{\tilde{X}(t)}(k)= \begin{cases}\mathrm{p}_{X}(k)[m(t)-m(t-k)] & \text { for } k<t \\ \mathrm{p}_{X}(k) m(t) & \text { for } k=t. \\ \mathrm{p}_{X}(k)[m(t)+1] & \text { for } k>t\end{cases}\label{4.67} \]
El término +1 en la expresión para\(k>t\) corresponde al punto más alto para lo dado\(k\) en la Figura 4.17a. Esto da cuenta de la posibilidad de que no haya llegadas hasta el momento\(t\). No es inmediatamente evidente eso\(\sum_{k} \mathrm{p}_{\tilde{X}(t)}(k)=1\), pero esto se puede verificar a partir de la ecuación de renovación, (4.52).
El teorema de Blackwell muestra que las probabilidades de llegada tienden a\(1 / \overline{X}\) como\(t \rightarrow \infty\), por lo que las probabilidades marginales limitantes para la edad y la duración se convierten
\[\lim _{\text {integer } t \rightarrow \infty} \mathrm{p}_{Z(t)}(i)=\frac{\mathrm{F}_{X}^{\mathrm{c}}(i)}{\overline{X}}.\label{4.68} \]
\[\lim _{\text {integer } t \rightarrow \infty} \mathrm{p}_{\widetilde{X}(t)}(k)=\frac{k\ \mathrm{p}_{X}(k)}{\overline{X}}.\label{4.69} \]
El valor esperado de\(Z(t)\) y también se\(\widetilde{X}(t)\) puede encontrar para todos\(t\) desde\ ref {4.62} y\ ref {4.63} respectivamente, pero no tienen una forma particularmente interesante. Los valores asintóticos como\(t \rightarrow \infty\) son más simples e interesantes. El valor asintótico esperado para la edad se deriva a continuación de (4.68). 22
\ [\ begin {alineado}
\ lim _ {\ texto {entero} t\ fila derecha\ infty}\ mathrm {E} [Z (t)] &=\ suma_ {i} i\ lim _ {\ text {entero} t\ rightarrow\ infty}\ mathrm {p} _ _ {Z (t)} (i)\\
&=\ frac {1} {\ overline {X}}\ suma_ {i=1} ^ {\ infty}\ suma_ {j=i+1} ^ {\ infty} i\ mathrm {p} _ _ {X} (j) =\ frac {1} {\ overline {X}}\ sum_ {j=2} ^ {\ infty}\ suma_ {i=1} ^ {j-1} i\ mathrm {p} _ _ {X} (j)\\
&=\ frac {1} {\ overline {X}}\ sum_ {j=2} ^ {\ infty}\ frac {j (j-1)} {2}\ mathrm {p} _ {X} (j)\\
&=\ frac {\ mathrm {E}\ izquierda [X^ {2}\ derecha]} {2\ overline {X}} -\ frac {1} {2}.
\ end {alineado}\ etiqueta {4.70}\]Esta edad promedio limitante del conjunto tiene la\(\mathrm{E}\left[X^{2}\right]\) misma dependencia que el promedio de tiempo en (4.16), pero, quizás sorprendentemente, se reduce de esa cantidad en 1/2. Para entender esto, tenga en cuenta que sólo hemos calculado la edad esperada a valores enteros de\(t\). Dado que las llegadas ocurren solo a valores enteros, la edad para cada función de muestra debe aumentar con la pendiente unitaria a medida que\(t\) se incrementa de un entero a otro. La edad esperada también aumenta, y luego en el siguiente valor entero, cae discontinuamente debido a la probabilidad de una llegada a ese siguiente entero. Así, el valor límite de\(\mathrm{E}[Z(t)]\) tiene forma de diente de sierra y el valor en cada discontinuidad es el lado inferior de esa discontinuidad. Al promediar esta edad esperada asintótica a lo largo de una unidad de tiempo, el promedio es\(\mathrm{E}\left[X^{2}\right] / 2 \overline{X}\), de acuerdo con (4.16).
Al igual que con el promedio de tiempo, la edad limitante esperada es infinita si\(\mathrm{E}\left[X^{2}\right]=\infty\). Sin embargo, para cada uno\(t\)\(Z(t) \leq t\), así\(\mathrm{E}[Z(t)]<\infty\) para todos\(t\), aumentando sin ataduras como\(t \rightarrow \infty\)
La duración asintótica esperada se deriva de manera similar, a partir de (4.69)
\ [\ begin {alineado}
\ lim _ {\ texto {entero} t\ fila derecha\ infty}\ mathrm {E} [\ tilde {X} (t)] &=\ suma_ {k}\ lim _ {\ texto {entero} t\ fila derecha\ infty} k\ mathrm {p} _ _ {\ tilde {X} (t)} (k)\
&=\ sum_ {k}\ frac {k^ {2}\ mathrm {p} _ {X} (k)} {\ overline {X}} =\ frac {\ mathrm {E}\ left [X^ {2}\ derecha]} {\ overline {X}}.
\ end {alineado}\ etiqueta {4.71}\]Esto concuerda con el promedio de tiempo en (4.17). La reducción en 1/2 vista en\ ref {4.70} no está presente aquí, ya que como\(t\) se incrementa en el intervalo\([t, t+1), X(t)\) permanece constante.
Dado que la edad promedio del conjunto asintótico difiere de la edad promedio del tiempo solo de una manera trivial, y la duración promedio del conjunto asintótico es la misma que la duración promedio de tiempo, podría parecer que hemos ganado poco con esta exploración de promedios conjuntos. Lo que hemos ganado, sin embargo, es un conjunto de resultados que se aplican a todos\(t\). Así muestran cómo (en principio) estos resultados convergen como\(t \rightarrow \infty\).
Edad y duración de la articulación: caso no aritmético
Los procesos de renovación no aritmética son matemáticamente más complicados que los procesos de renovación aritmética, pero los conceptos son los mismos. Comenzamos observando la probabilidad conjunta de la edad y duración, cada una a lo largo de un intervalo incremental. (véase la Figura 4.18 (a)).
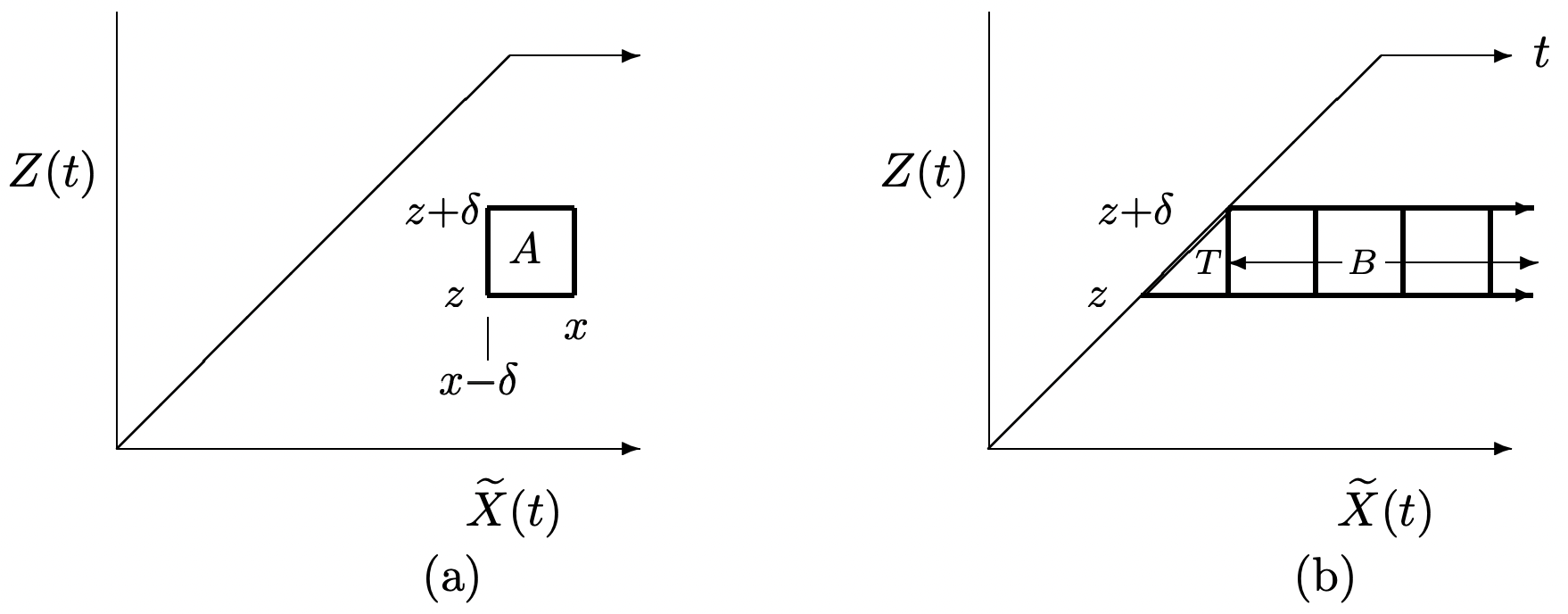
Considerar un proceso de renovación arbitrario con edad\(Z(t)\) y duración\(\widetilde{X}(t)\) en un momento dado\(t>0\). Deja que\(A\) sea el evento
\[A=\{z \leq Z(t)<z+\delta\} \bigcap\{x-\delta<\widetilde{X}(t) \leq x\}, \label{4.72} \]
dónde\(0 \leq z<z+\delta \leq t\) y\(z+2 \delta \leq x\). Entonces
\[\operatorname{Pr}\{A\}=[m(t-z)-m(t-z-\delta)]\left[\mathrm{F}_{X}(x)-\mathrm{F}_{X}(x-\delta)\right]\label{4.73} \]
Si además el proceso de renovación no es aritmético,
\[\lim _{t \rightarrow \infty} \operatorname{Pr}\{A\}=\frac{\left[\mathrm{F}_{X}(x)-\mathrm{F}_{X}(x-\delta)\right]}{\overline{X}}\label{4.74} \]
- Prueba
-
Obsérvese que\(A\) es el cuadro ilustrado en la Figura 4.18\ ref {a} y que bajo las condiciones dadas,\(\tilde{X}(t)>Z(t)\) para todos los puntos de muestreo en\(A\). Recordemos eso\(Z(t)=t-S_{N(t)}\) y\(\tilde{X}(t)=S_{N(t)+1}-S_{N(t)}=X_{N(t)+1}\), así también se\(A\) puede expresar como
\[A=\left\{t-z-\delta<S_{N(t)} \leq t-z\right\} \bigcap\left\{x-\delta<X_{N(t)+1} \leq x\right\}.\label{4.75} \]
Ahora argumentamos que también se\(A\) puede reescribir como
\[A=\bigcup_{n=1}^{\infty}\left\{\left\{t-z-\delta<S_{n} \leq t-z\right\} \bigcap\left\{x-\delta<X_{n+1} \leq x\right\}\right\}.\label{4.76} \]
Para ver esto, primero asuma que ocurre el evento en\ ref {4.75}. Entonces\(N(t)\) debe tener algún valor de muestra positivo\(n\), así se produce\ ref {4.76}. Siguiente asumir que el evento en\ ref {4.76} ocurre, lo que significa que uno de los eventos, digamos el\(n\) th, en la unión ocurre. Ya que\(S_{n+1}=S_{n}+X_{n+1}>t\), vemos que\(n\) es el valor muestral de\(S_{N(t)}\) y\ ref {4.75} debe ocurrir.
Para completar la prueba, debemos encontrar\(\operatorname{Pr}\{A\}\). Primera nota que\(A\) es una unión de eventos disjuntos. Es decir, aunque podría ocurrir más de una época de llegada en\((t-z-\delta, t-z]\), la siguiente época de llegada puede exceder\(t\) para solo una de ellas. Por lo tanto
\[\operatorname{Pr}\{A\}=\sum_{n=1}^{\infty} \operatorname{Pr}\left\{\left\{t-z-\delta<S_{n} \leq t-z\right\} \bigcap\left\{x-\delta<X_{n+1} \leq x\right\}\right\}.\label{4.77} \]
Para cada uno\(n\),\(X_{n+1}\) es independiente de\(S_{n}\), entonces
\ (\ begin {aligned}
\ operatorname {Pr}\ {\ {t-z-\ delta<&\ left. \ izquierda.s_ {n}\ leq t-z\ derecha\}\ bigcap\ izquierda\ {x-\ delta<x_ {n+1}\ leq x\ derecha\}\ derecha\}\
&=\ nombreoperador {Pr}\ izquierda\ {t-z-\ delta<s_ {n}\ leq t-z\ derecha\}\ izquierda [\ mathrm {F} _ {X} ^ {c} (x) -\ mathrm {F} _ {X} ^ {c} (x-\ delta]\ derecha..
\ end {alineado}\)Sustituyendo esto en\ ref {4.77} y usando\ ref {4.51} para sumar la serie, obtenemos
\(\operatorname{Pr}\{A\}=[m(t-z)-m(t-z-\delta)]\left[\mathrm{F}_{X}(x)-\mathrm{F}_{X}(x-\delta)\right]\).
Esto establece (4.73). Luego se establece el teorema de Blackwell (4.74).
Es curioso que\(\operatorname{Pr}\{A\}\) tenga una expresión de producto tan simple, donde un término depende sólo de la función\(m(t)\) y el otro sólo de la función de distribución\(\mathrm{F}_{X}\). Aunque el teorema es más útil ya que\(\delta \rightarrow 0\), la expresión es exacta para todos δ de tal manera que la región cuadrada\(A\) satisface las restricciones dadas (es decir,\(A\) se encuentra en la región trapezoidal semi-infinita indicada).
Z (t) para t finito: caso no aritmético
En esta sección, primero usamos el Teorema 4.7.2 para encontrar límites en la probabilidad incremental marginal de\(Z(t)\). Luego encontramos la función de distribución,\(\mathrm{F}_{Z(t)}(z)\), y el valor esperado,\(\mathrm{E}[Z(t)]\) de\(Z(t)\).
Para\(0 \leq z<z+\delta \leq t\), se mantienen los siguientes límites\(\operatorname{Pr}\{z \leq Z(t)<z+\delta\}\).
\[\operatorname{Pr}\{z \leq Z(t)<z+\delta\} \geq[m(t-z)-m(t-z-\delta)] \mathrm{F}_{X}^{c}(z+\delta)\label{4.78} \]
\[\operatorname{Pr}\{z \leq Z(t)<z+\delta\} \leq[m(t-z)-m(t-z-\delta)] \mathrm{F}_{X}^{\mathrm{c}}(z).\label{4.79} \]
- Prueba
-
Como se indica en la Figura 4.18 (b)\(\operatorname{Pr}\{z \leq Z(t)<z+\delta\}=\operatorname{Pr}\{T\}+\operatorname{Pr}\{B\}\), donde\(T\) está la región triangular,
\(T=\{z \leq Z(t)<z+\delta\} \bigcap\{Z(t)<\tilde{X}(t) \leq z+\delta\}\),
y\(B\) es la región rectangular
\(B=\{z \leq Z(t)<z+\delta\} \bigcap\{\widetilde{X}(t)>z+\delta\}\).
Es fácil de encontrar\(\operatorname{Pr}\{B\}\) sumando las probabilidades en\ ref {4.73} para los cuadrados indicados en la Figura 4.18 (b). El resultado es
\[\operatorname{Pr}\{B\}=[m(t-z)-m(t-z-\delta)] \mathrm{F}_{X}^{\mathrm{c}}(z+\delta)\label{4.80} \]
Ya que\(\operatorname{Pr}\{T\} \geq 0\), esto establece el límite inferior en (4.78). A continuación necesitamos un límite superior para\(\operatorname{Pr}\{T\}\) y comenzar por encontrar un evento que incluya\(T\).
\ (\ begin {alineado}
T &=\ {z\ leq Z (t) <z+\ delta\}\ bigcap\ {Z (t) <\ Widetilde {X} (t)\ leq z+\ delta\}\\
&=\ bigcup_ {n\ geq 1}\ left [\ left\ {t-z-\ Delta<s_ {n}\ leq t-q z\ derecha\}\ bigcap\ izquierda\ {t-s_ {n} <X_ {n+1}\ leq z+\ delta\ derecha\}\ derecha]\\
&\ subseteq\ bigcup_ {n\ geq 1}\ izquierda [\ izquierda\ {t-z-\ delta<s_ {n}\ leq t-z\ derecha\}\ bigcap\ izquierda\ {z<x_ {n+1}\ leq z+\ delta\ derecha\}\ derecha\,
\ final {alineada}\)donde la inclusión se deriva del hecho de que\(S_{n} \leq t-z\) para que se produzca el suceso de la izquierda, y esto implica que\(z \leq t-S_{n}\).
Usando el sindicato encuadernado, entonces tenemos
\ (\ begin {aligned}
\ operatorname {Pr}\ {T\} &\ leq\ left [\ suma_ {n\ geq 1}\ nombreoperador {Pr}\ izquierda\ {\ izquierda\ {t-z-\ Delta<s_ {n}\ leq t-z\ derecha\}\ derecha]\ izquierda [\ mathrm {F} _ {X} ^ {c} () -\ mathrm {F} _ {X} ^ {c} (z+\ delta)\ derecho]\ derecho. \\
&= [m (t-z) -m (t-z-\ delta)]\ left [\ mathrm {F} _ {X} ^ {c} (z) -\ mathrm {F} _ {X} ^ {c} (z+\ delta)\ derecha].
\ end {alineado}\)Combinando esto con (4.80), tenemos (4.79).
El siguiente corolario utiliza el Corolario 4.7.1 para determinar la función de distribución de\(Z(t)\). Después de la prueba se explicará la dependencia bastante extraña de la existencia de una integral de Stieltjes.
Si la integral Stieltjes\(\int_{t-z}^{t} \mathrm{~F}_{X}^{c}(t-\tau) d m(\tau)\) existe para dado\(t>0\) y\(0<z<t\), entonces
\[\operatorname{Pr}\{Z(t) \leq z\}=\int_{t-z}^{t} \mathrm{~F}_{X}^{\mathrm{c}}(t-\tau) d m(\tau)\label{4.81} \]
- Prueba
-
Primero, particione el intervalo\([0, z)\) en un número dado\(\ell\) de incrementos, cada uno de tamaño\(\delta=z / \ell\). Entonces
\(\operatorname{Pr}\{Z(t)<z\}=\sum_{k=0}^{\ell-1} \operatorname{Pr}\{k \delta \leq Z(t)<k \delta+\delta\}\).
Aplicando los límites en 4.78 y 4.79 a los términos de esta suma,
\[\operatorname{Pr}\{Z(t)<z\} \geq \sum_{k=0}^{\ell-1}[m(t-k \delta)-m(t-k \delta-\delta)] \mathrm{F}_{X}^{c}(k \delta+\delta)\label{4.82} \]
\[\operatorname{Pr}\{Z(t)<z\} \leq \sum_{k=0}^{\ell-1}[m(t-k \delta)-m(t-k \delta-\delta)] \mathrm{F}_{X}^{c}(k \delta)\label{4.83} \]
Estas son, respectivamente, sumas inferiores y superiores de Riemann para la integral Stieltjes\(\int_{0}^{z} \mathrm{~F}_{X}^{c}(t-\tau) d m(\tau)\). Así, si esta integral de Stieltjes existe, entonces, dejando\(\delta=z / \ell \rightarrow 0\),
\(\operatorname{Pr}\{Z(t)<z\}=\int_{t-z}^{t}{F}_{X}^{\mathrm{c}}(t-\tau) d m(\tau)\)
Esta es una convolución y así existe la integral Stieltjes a menos que\(m(\tau)\) y\(\mathrm{F}_{X}^{\mathrm{c}}(t-\tau)\) ambas tengan una discontinuidad en algunos\(\tau \in[0, z]\) (ver Ejercicio 1.12). Si no existe tal discontinuidad, entonces\(\operatorname{Pr}\{Z(t)<z\}\) no puede tener una discontinuidad en\(z\). Así, si existe la integral Stieltjes\(\operatorname{Pr}\{Z(t)<z\}=\operatorname{Pr}\{Z(t) \leq z\}\), y, para\(z<t\),
\(\mathrm{F}_{Z(t)}(z)=\int_{t-z}^{t} \mathrm{~F}_{X}^{\mathrm{c}}(t-\tau) d m(\tau)\)
El argumento anterior nos mostró que los valores de\(z\) a los que falla la integral de Stieltjes en\ ref {4.81} son aquellos en los que\(\mathrm{F}_{Z(t)}(z)\) tiene una discontinuidad escalonada. En estos valores sabemos que\(\mathrm{F}_{Z(t)}(z)\) (como función de distribución) debe tener el valor en la parte superior del paso (incluyendo así la probabilidad discreta de que\(\operatorname{Pr}\{Z(t)=z\}\)). Es decir, en cualquier punto\(z\) de discontinuidad donde no exista la integral Stieltjes,\(\mathrm{F}_{Z(t)}(z)\) es el límite 23 de\(\mathrm{F}_{Z(t)}(z+\epsilon)\) como se\(\epsilon>0\) acerca a 0. Otra forma de expresar esto es que para\(0 \leq z<t, \mathrm{~F}_{Z(t)}(z)\) es el límite de la suma superior de Riemann en el lado derecho de (4.83).
El siguiente corolario utiliza un argumento casi idéntico para encontrar\(\mathrm{E}[Z(t)]\). Como veremos, la integral Stieltjes no logra existir en aquellos valores de t en los que existe una probabilidad discreta positiva de llegada. El valor esperado en estos puntos es la suma menor de Riemann para la integral de Stieltjes.
Si la integral Stieltjes\(\int_{0}^{t} \mathrm{~F}_{X}^{c}(t-\tau) d m(\tau)\) existe para dado\(t>0\), entonces
\[\mathrm{E}[Z(t)]=\mathrm{F}_{X}^{c}(t)+\int_{0}^{t}(t-\tau) \mathrm{F}_{X}^{c}(t-\tau) d m(\tau)\label{4.84} \]
- Prueba
-
Tenga en cuenta que\(Z(t)=t\) si y solo si\(X_{1}>t\), que tiene probabilidad\(\mathrm{F}_{X}^{\mathrm{c}}(t)\). Para los otros valores posibles de\(Z(t)\),\([0, t)\) dividimos en intervalos\(\ell\) iguales de longitud\(\delta=t / \ell\) cada uno. Entonces\(\mathrm{E}[Z(t)]\) se puede limitar más bajo por
\ (\ begin {alineado}
\ mathrm {E} [Z (t)] &\ left. \ geq\ mathrm {F} _ _ {X} ^ {c} (t) +\ suma_ {k=0} ^ {\ ell-1} k\ delta\ nombreoperador {Pr}\ {k\ delta\ leq Z (t) <k\ delta+\ delta\}\ derecho\}\
&\ geq\ mathrm {F} _ _ {X} ^ {c} (t) +\ sum_ {k=0} ^ {\ ell-1} k\ delta [m (t-k\ delta) -m (t-k\ delta-\ delta)]\ mathrm {F} _ {X} ^ {c} (k\ delta+\ delta).
\ end {alineado}\)donde usamos 4.78 para el segundo paso. Del mismo modo,\(\mathrm{E}[Z(t)]\) puede estar delimitado por
\ (\ begin {alineado}
\ mathrm {E} [Z (t)] &\ leq\ mathrm {F} _ {X} ^ {\ mathrm {c}} (t) +\ suma_ {k=0} ^ {\ ell-1} (k\ delta+\ delta)\ nombreoperador {Pr}\ {k\ delta\ leq Z (t) <k\ delta+\ delta\}\}\\
&\ leq\ mathrm {F} _ _ {X} ^ {\ mathrm {c}} (t) +\ sum_ {k=0} ^ {\ ell-1} (k\ delta+\ delta) [m (t-k\ delta) -m (t-k \ delta-\ delta)]\ mathrm {F} _ {X} ^ {c} (k\ delta).
\ end {alineado}\)donde usamos 4.79 para el segundo paso. Éstos proporcionan sumas de Riemann inferior y superior a los Stieltjes integrales en (4.81), completando la prueba de la misma manera que el corolario anterior.
Z (t) como t → ∞: caso no aritmético
A continuación, para los procesos de renovación no aritmética, queremos encontrar los valores limitantes, as\(t \rightarrow \infty\), for\(\mathrm{F}_{Z(t)}(z)\) y\(\mathrm{E}[Z(T)]\). Ignorando temporalmente cualquier sutileza sobre el límite, primero vemos\(d m(t)\) como yendo a\(\frac{d t}{\overline{X}}\) como\(t \rightarrow \infty\). Así, a partir de (4.81),
\[\lim _{t \rightarrow \infty} \operatorname{Pr}\{Z(t) \leq z\}=\frac{1}{\overline{X}} \int_{0}^{z} \mathrm{~F}_{X}^{\mathrm{c}}(\tau) d \tau\label{4.85} \]
Si X tiene un PDF, esto simplifica aún más
\[\lim _{t \rightarrow \infty} f_{Z(t)}(z)=\frac{1}{\overline{X}} f_{X}(z)\label{4.86} \]
Obsérvese que esto concuerda con el resultado promedio de tiempo en (4.29). Tomar estos límites con cuidado requiere más matemáticas de las que parece justificadas aquí, sobre todo porque el resultado utiliza el teorema de Blackwell, que no fue probado aquí. Así declaramos (sin pruebas) otro teorema, equivalente al teorema de Blackwell, llamado teorema de renovación clave, que simplifica tomar este tipo de límite. Esencialmente, el teorema de Blackwell es más fácil de interpretar, pero el teorema de renovación clave suele ser más fácil de usar.
Dejar\(r(x) \geq 0\) ser una función integrable directamente Riemann, y dejar que\(m(t)=\mathrm{E}[N(t)]\) para un proceso de renovación no aritmética. Entonces
\[\lim _{t \rightarrow \infty} \int_{\tau=0}^{t} r(t-\tau) d m(\tau)=\frac{1}{\overline{X}} \int_{0}^{\infty} r(x) d x\label{4.87} \]
Primero explicamos lo que significa directamente integrable Riemann. Si\(r(x)\) es distinto de cero solo sobre límites finitos, digamos\([0, b]\), entonces la integración directa de Riemann significa lo mismo que la integración ordinaria de Riemann (como se aprendió en el cálculo elemental). Sin embargo, si\(r(x)\) es distinto de cero\([0, \infty)\), entonces la integral ordinaria de Riemann (si existe) es el resultado de integrar de 0 a\(b\) y luego tomar el límite como\(b \rightarrow \infty\). La integral directa de Riemann (si existe) es el resultado de tomar una suma de Riemann sobre toda la media línea,\([0, \infty)\) y luego tomar el límite a medida que la cuadrícula se vuelve más fina. El ejercicio 4.25 da un ejemplo de una función simple pero extraña que es Riemann integrable pero no directamente Riemann integrable. Si\(r(x) \geq 0\) puede estar delimitado por una función integrable Riemann decreciente, sin embargo, entonces, como se muestra en el Ejercicio 4.25,\(r(x)\) debe ser directamente integrable de Riemann. La conclusión es que restringir\(r(x)\) para ser directamente integrable Riemann no es una restricción importante.
A continuación interpretamos el teorema. Si\(m(t)\) tiene un derivado, entonces el teorema de Blackwell sugeriría eso\(d m(t) / d t \rightarrow(1 / \overline{X}) d t\), lo que lleva a\ ref {4.87} (dejando fuera los detalles matemáticos). Por otro lado, si\(X\) es discreto pero no aritmético, entonces\(d m(t) / d t\) puede ser visto intuitivamente como una secuencia de impulsos que se hacen más pequeños y más estrechamente espaciados como\(t \rightarrow \infty\). \(r(t)\)Actúa entonces como un filtro suavizante que\(t \rightarrow \infty\), como, suaviza estos pequeños impulsos. El teorema dice que el suavizado requerido ocurre siempre que\(r(t)\) sea directamente integrable por Riemann. El teorema no afirma que la integral Stieltjes exista para todos\(t\), sino solo que existe el límite. Para la mayoría de las aplicaciones a intervalos discretos entre renovaciones, la integral Stieltjes no existe en todas partes. Usando el teorema de renovación clave, finalmente podemos determinar la función de distribución y el valor esperado de\(Z(t)\) as\(t \rightarrow \infty\). Estos promedios de conjunto limitantes son, por supuesto, iguales a los promedios de tiempo encontrados anteriormente.
Para cualquier proceso de renovación no aritmética, la función de distribución limitante y el valor esperado de la edad\(Z(t)\) están dados por
\[\lim _{t \rightarrow \infty} \mathrm{F}_{Z(t)}(z)=\frac{1}{\overline{X}} \int_{0}^{z} \mathrm{~F}_{X}^{\mathrm{c}}(x) d x\label{4.88} \]
Además, si\(\mathrm{E}\left[X^{2}\right]<\infty\), entonces
\[\lim _{t \rightarrow z} \mathrm{E}[Z(t)]=\frac{\mathrm{E}\left[X^{2}\right]}{2 \overline{X}}\label{4.89} \]
- Prueba
-
Para cualquier dado\(z>0\), vamos\(r(x)=\mathrm{F}_{X}^{\mathrm{c}}(x)\) para\(0 \leq x \leq z\) y\(r(x)=0\) en otra parte. Entonces\ ref {4.81} se convierte
\(\operatorname{Pr}\{Z(t) \leq z\}=\int_{0}^{t} r(t-\tau) d m(\tau)\)
Tomando el límite como\(t \rightarrow \infty\),
\ [\ begin {alineado}
\ lim _ {t\ fila derecha\ infty}\ nombreoperador {Pr}\ {Z (t)\ leq z\} &=\ lim _ {t\ fila derecha\ infty}\ int_ {0} ^ {t} r (t-\ tau) d m (\ tau)\\
&=\ frac {1} {\ overline {X}}\ int_ {0} ^ {\ infty} r (x) d x=\ frac {1} {\ overline {X}}\ int_ {0} ^ {z}\ mathrm {~F} _ _ {X} ^ {c} (x) d x
\ end {alineado}\ etiqueta {4.90}\]donde en\ ref {4.90} utilizamos el hecho de que\(\mathrm{F}_{X}^{c}(x)\) está disminuyendo para justificar el uso (4.87). Esto establece (4.88).
Para establecer (4.89), volvemos a utilizar el teorema de renovación clave, pero aquí dejamos\(r(x)=x \mathrm{~F}_{X}^{\mathrm{c}}(x)\). El ejercicio 4.25 muestra que\(x \mathrm{~F}_{X}^{c}(x)\) es directamente Riemann integrable si\(\mathrm{E}\left[X^{2}\right]<\infty\). Luego, tomando el límite de (4.84 y luego usando (4.87), tenemos
\ (\ comenzar {alineado}
\ lim _ {t\ fila derecha\ infty}\ mathrm {E} [Z (t)] &=\ lim _ {t\ fila derecha\ infty}\ mathrm {F} _ _ {X} ^ {c} (t) +\ int_ {0} ^ {t} r (t-\ tau) d m (\ tau)\\
&= {1} {\ overline {X}}\ int_ {0} ^ {\ infty} r (x) d x=\ frac {1} {\ overline {X}}\ int_ {0} ^ {\ infty} x\ mathrm {~F} _ _ {X} ^ {c} ( x) d x
\ final {alineado}\)Integrando esto por partes, obtenemos (4.89).
Funciones arbitrarias de renovación-recompensa: caso no aritmético
Si omitimos toda la precisión matemática de las tres subsecciones anteriores, obtenemos una imagen muy sencilla. Comenzamos con (4.72), lo que dio la probabilidad de una región cuadrada incremental A en el\((Z(t), \widetilde{X}(t))\) plano para dado\(t\). Luego convertimos varias sumas sobre una cuadrícula cada vez más fina de tales regiones en integrales de Stieltjes. Estas integrales evaluaron la distribución y el valor esperado de la edad a valores arbitrarios de\(t\). Por último, el teorema de renovación clave nos dejó tomar el límite de estos valores como\(t \rightarrow \infty\).
En esta subsección, pasaremos por el mismo procedimiento para una función de recompensa arbitraria, digamos\(R(t)=\mathcal{R}(Z(t), \widetilde{X}(t))\), y mostraremos cómo encontrar\(\mathrm{E}[R(T)]\). Tenga en cuenta que\(\mathrm{Pr}\{Z(t)\leq z\}=\mathrm{E}\left[\mathbb{I}_{Z(t) \leq z}\right]\) es un caso especial de\(\mathrm{E}[R(T)]\) donde\(R(t)\) se elige estar\(\mathbb{I}_{Z(t) \leq z}\). Del mismo modo, encontrar la función de distribución en un argumento dado para cualquier rv se puede convertir a la expectativa de una función indicadora. Así, contar con una metodología para encontrar la expectativa de una función de recompensa arbitraria también abarca funciones de distribución y muchas otras cantidades de interés.
Dejaremos de lado todos los argumentos limitantes aquí sobre la conversión de sumas incrementales finitas de áreas en integrales, ya que hemos visto cómo hacerlo en el tratamiento\(Z(t)\). Para que este caso general sea más transparente, utilizamos la siguiente taquigrafía para A cuando es incrementalmente pequeña:
\[\operatorname{Pr}\{A\}=m^{\prime}(t-z) f_{X}(x) d x d z,\label{4.91} \]
donde, si existen los derivados,\(m^{\prime}(\tau)=d m(\tau) / d \tau\) y\(f_{X}(x)=d \mathrm{~F}_{X}(x) / d x\). Si las derivadas no existen, podemos ver\(m^{\prime}(\tau)\) y\(f_{X}(x)\) como funciones generalizadas incluyendo impulsos, o, más apropiadamente, verlas simplemente como taquigrafía. Después de usar la taquigrafía como guía, podemos poner los resultados en forma de integrales de Stieltjes y verificar los detalles matemáticos en cualquier nivel que parezca apropiado.
Esto lo hacemos primero para el ejemplo de la función de distribución de duración,\(\operatorname{Pr}\left\{\widetilde{X}(t) \leq x_{0}\right\}\), donde primero asumimos eso\(x_{0} \leq t\). Como se ilustra en la Figura 4.19, la función de recompensa correspondiente\(R(t)\) es 1 en la región triangular donde\(\tilde{X}(t) \leq x_{0}\) y\(Z(t)<\tilde{X}(t)\). Es 0 en otra parte.
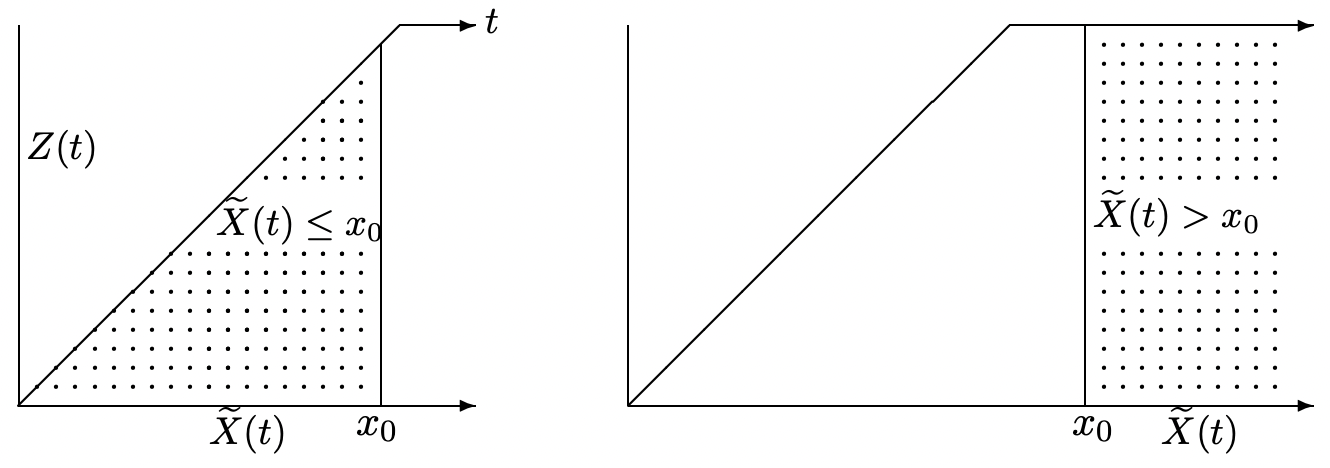
\ [\ begin {alineado}
\ nombreoperador {Pr}\ izquierda\ {\ tilde {X} (t)\ leq x_ {0}\ derecha\} &=\ int_ {z=0} ^ {x_ {0}}\ int_ {x=z} ^ {x_ {0}} m^ {\ prime} (t-z)\ mathrm {f} _ {X} (x) d x d z\\
&=\ int_ {z=0} ^ {x_ {0}} m^ {\ prime} (t-z)\ izquierda [\ mathrm {F} _ _ {X}\ izquierda (x_ {0}\ derecha) -\ mathrm {F} _ _ {X} (z)\ derecha] d z\\
&=\ mathrm {F} _ {X}\ izquierda (x_ {0}\ derecha)\ izquierda [m (t) -m\ izquierda (t-x_ {0}\ derecha)\ derecha] -\ int_ {t-x_ {0}} ^ {t}\ mathrm {~F} _ _ {X} (t-\ tau) d m (\ tau)
\ final {alineado}\ etiqueta 4.92}\]
Para el caso contrario, donde\(x_{0}>t\), es más fácil de encontrar\(\operatorname{Pr}\left\{\tilde{X}(t)>x_{0}\right\}\). Como se muestra en la figura, esta es la región donde\(0 \leq Z(t) \leq t\) y\(\tilde{X}(t)>x_{0}\). Aquí hay una sutileza en que las áreas incrementales que estamos usando solo son válidas para\(Z(t)<t\). Si la edad es igual a\(t\), entonces no se han producido renovaciones en\((0, t]\), así que eso\(\operatorname{Pr}\left\{\tilde{X}(t)>x_{0} ; Z(t)=t\right\}=\mathrm{F}_{X}^{c}\left(x_{0}\right)\). Por lo tanto
\ [\ begin {alineado}
\ nombreoperador {Pr}\ izquierda\ {\ tilde {X} (t) >x_ {0}\ derecha\} &=\ mathrm {F} _ {X} ^ {c}\ izquierda (x_ {0}\ derecha) +\ int_ {z=0} ^ ^ {t^ {-}}\ int_ {x=x_ {0}} ^ ^ {\ infty} m^ {\ prime} (t-z)\ mathrm {f} _ {X} (x) d x d z\\
&=\ mathrm {F} _ {X} _ {X} ^ {c}\ izquierda (x_ {0}\ derecha) +m (t)\ mathrm {F} _ {X} ^ {c}\ izquierda (x_ {0}\ derecha)
\ end {alineado}\ etiqueta {4.93}\]
Como prueba de cordura, la ecuación de renovación, (4.53), puede ser utilizada para mostrar que la suma de\ ref {4.92} y\ ref {4.93} at\(x_{0}=t\) es igual a 1 (como deben ser si las ecuaciones son correctas).
Ya podemos tomar el límite,\(\lim _{t \rightarrow \infty} \operatorname{Pr}\left\{\tilde{X}(t) \leq x_{0}\right\}\). Para cualquier dado\(x_{0}\),\ ref {4.92} se mantiene para suficientemente grande\(t\), y el teorema de renovación clave se puede utilizar ya que la integral tiene un rango finito. Por lo tanto,
\ [\ begin {alineado}
\ lim _ {t\ fila derecha\ infty}\ nombreoperador {Pr}\ izquierda\ {\ tilde {X} (t)\ leq x_ {0}\ derecha\} &=\ frac {1} {\ overline {X}}\ izquierda [x_ {0}\ mathrm {~F} _ _ {X}\ izquierda (x_ {0}}\ derecha) -\ int_ {0} ^ {x_ {0}}\ mathrm {~F} _ _ {X} (x) d x\ derecha]\\
&=\ frac {1} {\ overline {X}}\ int_ {0} ^ {x_ {0}}\ izquierda [\ mathrm {~F} _ _ {X}\ izquierda (x_ {0}\ derecha) -\ mathrm {F} _ _ {X} (x)\ derecha] d x\\
&=\ frac {1} {\ overline {X}}\ int_ {0} ^ {x_ {0}}\ izquierda [\ mathrm {~F} _ _ {X} ^ {c} (x) -izquierda [\ mathrm {~F} _ {X} ^ {c} (x) d F_ {X} ^ {c}\ izquierda (x_ {0}\ derecha)\ derecha] d x
\ final {alineado}\ etiqueta {4.94}\]
Es fácil ver que el lado derecho de\ ref {4.94} va aumentando de 0 a 1 con el incremento\(x_{0}\), es decir, es una función de distribución.
Después de este ejemplo, ahora es sencillo anotar el valor esperado de una función de renovación-recompensa arbitraria\(R(t)\) cuyo valor de muestra en\(Z(t)=z\) y\(X(t)=x\) se denota por\(\mathcal{R}(z, x)\). Tenemos
\[\mathrm{E}[R(t)]=\int_{x=t}^{\infty} \mathcal{R}(t, x) d \mathrm{~F}_{X}(x)+\int_{z=0}^{t} \int_{x=z}^{\infty} \mathcal{R}(z, x) d \mathrm{~F}_{X}(x) d m(t-z)\label{4.95} \]
El primer término anterior surge de la sutileza comentada anteriormente para el caso donde\(Z(t)=t\). El segundo término es simplemente la integral sobre el área trapezoidal semiinfinita en la Figura 4.19.
El análisis hasta este punto se aplica tanto a los casos aritméticos como a los no aritméticos, pero ahora debemos asumir nuevamente que el proceso de renovación es no aritmético. Si la integral interna, es decir\(\int_{x=z}^{\infty} \mathcal{R}(z, x) d \mathrm{~F}_{X}(x)\), en función de\(z\), es directamente integrable Riemann, entonces no sólo se puede aplicar el teorema de renovación clave a este segundo término, sino que también el primer término debe acercarse a 0 como\(t \rightarrow \infty\). Así, el límite de\ ref {4.95} como\(t \rightarrow \infty\) es
\[\lim _{t \rightarrow \infty} \mathrm{E}[R(t)]=\frac{1}{\overline{X}} \int_{z=0}^{\infty} \int_{x=z}^{\infty} \mathcal{R}(z, x) d \mathrm{~F}_{X}(x) d z\label{4.96} \]
Esta es la misma expresión que se encontró para la recompensa de renovación promedio de tiempo en el Teorema 4.4.1. Así, como se indicó anteriormente, ahora podemos equiparar cualquier resultado promedio de tiempo para el caso no aritmético con el promedio de conjunto limitante correspondiente, y en ambos casos se han derivado las mismas ecuaciones.
Como ejemplo sencillo de (4.96), vamos\(\mathcal{R}(z, t)=x\). Entonces\(\mathrm{E}[R(t)]=\mathrm{E}[\tilde{X}(t)]\) y
\ [\ begin {alineado}
\ lim _ {t\ rightarrow\ infty}\ mathrm {E} [\ tilde {X} (t)] &=\ frac {1} {\ overline {X}}\ int_ {z=0} ^ {\ infty}\ int_ {x=z} ^ {\ infty} x d\ mathrm {~F} _ _ {X} (x) d z=\ int_ {x=0} ^ {\ infty}\ int_ {z=0} ^ {x} x d z d\ mathrm {~F} _ _ {X} (x)\\
&=\ frac {1} {\ overline {X}}\ int_ {x=0} ^ {\ infty} x^ {2} d\ mathrm {~F} _ _ {X} (x) =\ frac {\ mathrm {E}\ izquierda [X^ {2}\ derecha]} {\ overline {X}}
\ final {alineado}\ etiqueta {4.97}\]
Después de calcular la integral anterior intercambiando el orden de integración, podemos retroceder y afirmar que el teorema de renovación clave aplica si\(\mathrm{E}\left[X^{2}\right]\) es finito. Si es infinito, entonces no es difícil ver que\(\lim _{t \rightarrow \infty} \mathrm{E}[\tilde{X}(t)]\) es infinito también.
Ha sido importante, y teóricamente tranquilizador, poder encontrar promedios de conjuntos para funciones de renovación-recompensa no aritméticas en el límite de grandes\(t\) y mostrar (no es sorprendente) que son los mismos que los resultados promedio de tiempo. Sin embargo, los resultados promedio del conjunto son bastante complicados, y es aconsejable verificar los resultados obtenidos de esa manera con los resultados promedio de tiempo correspondientes.
21 Esto debe parecerle un quisquilloso matemático a muchos lectores. Sin embargo,\(m(t)\) es el número esperado de renovaciones en\((0, t]\), y cómo\(m(t)\) varía con\(t\), es central para este capítulo y sigue reapareciendo.
22 Encontrar las expectativas limitantes de los PMF limitantes requiere intercambiar un límite con una expectativa. Esto puede justificarse (tanto en\ ref {4.70} como en (4.71)) asumiendo que\(X\) tiene un segundo momento finito y señalando que todos los términos involucrados son positivos, eso\(\operatorname{Pr}\{\text { arrival at } j\} \leq 1\) para todos\(j\), y eso\(\mathrm{p}_{X}(k) \leq 1\) para todos\(k\).
23 Esto parece ser matemática bastante abstracta, pero como ingenieros, a menudo evaluamos funciones con discontinuidades escalonadas ignorando los valores en las discontinuidades o evaluando estos puntos por medios adhoc.


