7.4: Propiedades del DTFS

Introducción

En este módulo discutiremos las propiedades básicas de la Serie de Fourier de Tiempo Discreto. Comenzaremos refrescando su memoria de nuestras ecuaciones básicas de la serie de Fourier:

\[f[n]=\sum_{k=0}^{N-1} c_{k} e^{j \omega_{0} k n} \nonumber \]

\[c_{k}=\frac{1}{\sqrt{N}} \sum_{n=0}^{N-1} f[n] e^{-\left(j \frac{2 \pi}{N} k n\right)} \nonumber \]

Dejar\(\mathscr{F}(\cdot)\) denotar la transformación de\(f[n]\) a los coeficientes de Fourier

\[\mathscr{F}(f[n])=c_{k} \quad, \quad k \in \mathbb{Z} \nonumber \]

\(\mathscr{F}(\cdot)\)mapea funciones complejas valoradas a secuencias de números complejos.

Linealidad

\(\mathscr{F}(\cdot)\)es una transformación lineal.

Teorema\(\PageIndex{1}\)

Si\(\mathscr{F}(f[n])=c_{k}\) y\(\mathscr{F}(g[n])=d_{k}\). Entonces

\[\mathscr{F}(\alpha f[n])=\alpha c_{k} \quad, \quad \alpha \in \mathbb{C} \nonumber \]

y

\[\mathscr{F}(f[n]+g[n])=c_{k}+d_{k} \nonumber \]

Prueba

Fácil. Justa linealidad de integral.

\ [\ begin {align}
\ mathscr {F} (f [n] +g [n]) &=\ sum_ {n=0} ^ {N} (f [n] +g [n]) e^ {-\ left (j\ omega_ {0} k n\ derecha)}, k\ in\ mathbb {Z}\ nonumber\\
&=\ frac {1} {N}\ suma_ {n=0} ^ {N} f [n] e^ {-\ izquierda (j\ omega_ {0} k n\ derecha)} +\ frac {1} {N}\ suma_ {n=0} ^ {N} g [n] e^ {-\ izquierda (j\ omega_ {0} k n\ derecha)}, k\ in \ mathbb {Z}\ nonumber\\
&=c_ {k} +d_ {k}, k\ in\ mathbb {Z}\ nonumber\\
&=c_ {k} +d_ {k}
\ end {align}\ nonumber\]

Desviación

El desplazamiento en el tiempo equivale a un desplazamiento de fase de los coeficientes de Fourier.

Teorema\(\PageIndex{2}\)

\(\mathscr{F}\left(f\left[n-n_{0}\right]\right)=e^{-\left(j \omega_{0} k n_{0}\right)} c_{k}\)si\(c_{k}=\left|c_{k}\right| e^{j \angle\left(c_{k}\right)}\), entonces

\[\left|e^{-\left(j \omega_{0} k n_{0}\right)} c_{k}\right|=\left|e^{-\left(j \omega_{0} k n_{0}\right)}\right|\left|c_{k}\right|=\left|c_{k}\right| \nonumber \]

\[ \angle\left(e^{-\left(j \omega_{0} n_{0} k\right)}\right)=\angle\left(c_{k}\right)-\omega_{0} n_{0} k \nonumber \]

Prueba

\ [\ begin {align}
\ mathscr {F}\ izquierda (f\ izquierda [n-n_ {0}\ derecha]\ derecha) &=\ frac {1} {N}\ suma_ {n=0} ^ {N} f\ izquierda [n-n_ {0}\ derecha] e^ {-\ izquierda (j\ omega_ {0} k n\ derecha)},\ k quad\ en\ mathbb {Z}\ nonumber\\
&=\ frac {1} {N}\ suma_ {n=-n_ {0}} ^ {n-n_ {0}} f\ izquierda [n-n_ {0}\ derecha] e^ {-\ izquierda (j\ omega_ {0} k\ izquierda (n-n_ {0}\ derecha)\ derecha)} e^ {-\ izquierda (j\ omega_ {0} k n_ {0}\ derecha)}\ quad,\ quad k\ in\ mathbb {Z}\ nonumber\\
&=\ frac {1} {N}\ sum_ {n=-n_ {0}} ^ {n-n_ {0}} [f\ tilde {n}] e^ {-\ izquierda (j\ omega_ {0} k\ tilde {n}\ derecha)} e^ {-\ izquierda (j\ omega_ {0} k n_ {0}\ derecha)}\ quad,\ quad k\ in\ mathbb {Z}\ nonumber\\
&=e^ {-\ izquierda (j\ omega_ {0} k\ tilde {n}\ derecha)} c_ {k}\ quad,\ quad k\ in\ mathbb {Z}
\ end {align}\ nonumber\]

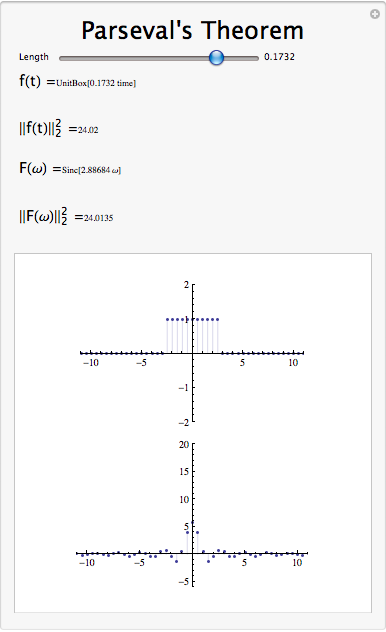
Relación de Parseval

\[ \sum_{n=0}^{N}(|f[n]|)^{2}=N \sum_{k=0}^{N-1}\left(\left|c_{k}\right|\right)^{2} \nonumber \]

La relación de Parseval nos dice que la energía de una señal es igual a la energía de su transformada de Fourier.

Nota

Parseval nos dice que la serie de Fourier se mapea\(L^2[0,N]\) a\(l^2\).

Figura\(\PageIndex{1}\)

Ejercicio\(\PageIndex{1}\)

\(f[n]\)Para tener “energía finita”, ¿cómo\(c_k\) hacen los\( k \rightarrow \infty\)?

Contestar

\(\left(\left|c_{k}\right|\right)^{2}<\infty\)para\(f[n]\) tener energía finita.

Ejercicio\(\PageIndex{2}\)

Si\(\forall k,|k|>0:\left(c_{k}=\frac{1}{k}\right)\), ¿es\(f \in L^{2} [ [ 0, N ] ] \)?

Contestar

Sí, porque\((|c_k|)^2=\frac{1}{k^2}\), que es sumable.

Ejercicio\(\PageIndex{3}\)

Ahora, si\(\forall k,|k|>0:\left(c_{k}=\frac{1}{\sqrt{k}}\right)\),\(f \in L^{2} [ [ 0, N ] ]\) ¿es?

Contestar

No, porque\((|c_k|)^2=\frac{1}{k}\), que no es sumable.

La tasa de decaimiento de la serie de Fourier determina si\(f[n]\) tiene energía finita.

Demostración del Teorema de Parsevals

Figura\(\PageIndex{2}\): Interactuar (cuando esté en línea) con un CDF de Mathematica demostrando el Teorema de Análisis. Para descargar, haga clic derecho y guárdalo como .cdf.

Propiedades de simetría

Regla\(\PageIndex{1}\): Even Signals

\(f[n] = f[-n]\)

\(\left\|c_{k}\right\|=\left\|c_{-k}\right\|\)

Prueba

\ (\ begin {align}
c_ {k} =&\ frac {1} {N}\ suma_ {0} ^ {N} [n]\ exp\ left [-j\ omega_ {0} k n\ derecha]\ nonumber\\
=&\ frac {1} {N}\ sum_ {0} ^ {\ frac {N} {2}} f [n]\ exp\ izquierda [-j\ omega_ {0} k n\ derecha] +\ frac {1} {N}\ suma_ {\ frac {N} {2}} ^ {N} f [n]\ exp\ izquierda [-j\ omega_ {0} k n\ derecha]\ nonumber\\
=&\ frac {1} {N}\ sum_ {0} ^ {\ frac {N} {2}} f [-n]\ exp\ left [-j\ omega_ {0} k n\ derecha] +\ frac {1} {N}\ sum_ {\ frac {N} {2}} ^ {N} f [-n]\ exp\ izquierda [-j\ omega_ {0} k n\ derecha]\ nonumber\\
=&\ frac {1} {N}\ suma_ {0} ^ {N} [n]\ izquierda [\ exp\ izquierda [j\ omega_ {0} k n\ derecha] +\ exp\ izquierda [-j\ omega_ {0} k n\ derecha]\ derecha]\ nonumber\\
=&\ frac {1} {N}\ suma_ {0} ^ {N} [n] 2\ cos\ izquierda [\ omega_ {0} k n\ derecha]
\ end {align}\)

Regla\(\PageIndex{2}\): Odd Signals

\(f[n]=-f[-n]\)

\(c_{k}=c_{-k}^*\)

Prueba

\ (\ begin {align}
c_ {k} =&\ frac {1} {N}\ sum_ {0} ^ {N} f [n]\ exp\ left [-\ mathrm {j}\ omega_ {0} k n\ derecha]\ nonumber\\
=&\ frac {1} {N}\ sum_ {0} ^ {\ frac {N} {2}} f [n]\ exp\ izquierda [-\ mathrm {j}\ omega_ {0} k n\ derecha] +\ frac {1} {N}\ sum_ {\ frac {N} {2}} ^ {N} f [n]\ exp\ left [-\ mathrm {j}\ omega_ {0} k n\ derecha]\ nonumber\\
=&\ frac {1} {N}\ suma_ {0} ^ {\ frac {N} {2}} f [n]\ exp\ izquierda [-\ mathrm {j}\ omega_ {0} k n\ derecha] -\ frac {1} {N} {N}\ sum_ {\ frac {N} {2} ^ {N} f [-n]\ exp\ izquierda [\ mathrm {j}\ omega_ {0} k n\ derecha]\ nonumber\\
=&-\ frac {1} {N}\ sum_ {0} ^ {N} f [n]\ left [\ exp\ left [\ mathrm {j}\ omega_ {0} k n\ derecha] -\ exp\ izquierda [-\ mathrm {j}\ omega_ {0} k n\ derecha]\ derecha]\ nonumber\\
=&-\ frac {1} {N}\ sum_ {0} ^ {N} f [n] 2\ nombreoperador {j\ sin}\ izquierda [\ omega_ {0} k n\ derecha]
\ end align {}\)

Regla\(\PageIndex{3}\): Real Signals

\(f[n] = f^*[n]\)

\(c_k = c_{-k}^*\)

Prueba

\ (\ displaystyle {\ begin {align}
c_ {k} =&\ frac {1} {N}\ sum_ {0} ^ {N} f [n]\ exp\ left [-\ mathrm {j}\ omega_ {0} k n\ derecha]\ nonumber\\
=&\ frac {1} {N}\ sum_ {0} ^ {\ frac N} {2}} f [n]\ exp\ izquierda [-\ mathrm {j}\ omega_ {0} k n\ derecha] +\ frac {1} {N} {N}\ sum_ {\ frac {N} {2}} ^ {N} f [n]\ exp\ left [-\ mathrm {j}\ omega_ {0} k n\ derecha]\ nonumber\\
=&\ frac {1} {N}\ suma_ {0} ^ {\ frac {N} {2}} f [-n]\ exp\ izquierda [-\ mathrm {j}\ omega_ {0} k n\ derecha] +\ frac {1} {N}\ n sum_ {\ frac {} {2}} ^ {N} f [-n]\ exp\ izquierda [-\ mathrm {j}\ omega_ {0} k n\ derecha]\ nonumber\\
=&\ frac {1} {N}\ sum_ {0} ^ {N} f [n]\ left [\ exp\ left [\ mathrm {j}\ omega_ {0} k n\ derecha] +\ exp\ izquierda [-\ mathrm {j}\ omega_ {0} k n\ derecha]\ derecha]\ nonumber\\
=&\ frac {1} {N}\ sum_ {0} ^ {N} f [n] 2\ cos\ izquierda [\ omega_ {0} k\ derecha]
\ final {align}}\)

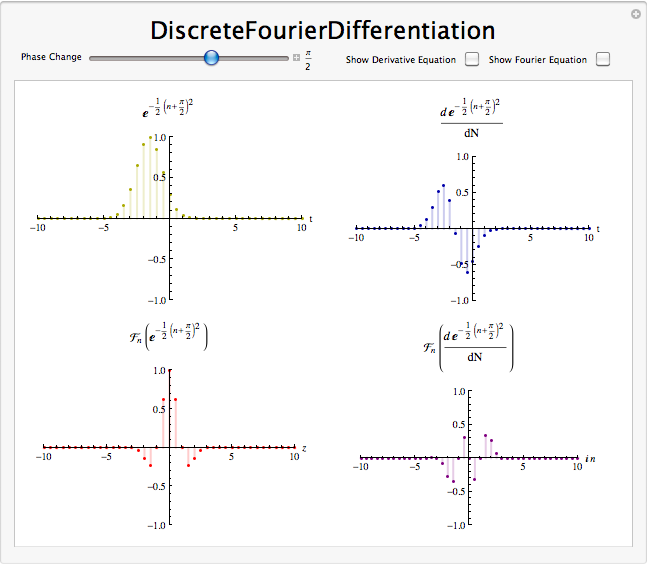
Diferenciación en el Dominio de Fourier

\[\left(\mathscr{F}(f[n])=c_{k}\right) \Rightarrow\left(\mathscr{F}\left(\frac{\mathrm{d} f[n]}{\mathrm{d} n}\right)=j k \omega_{0} c_{k}\right) \nonumber \]

Desde

\[f[n]=\sum_{i=0}^{N} c_{k} e^{j \omega_{0} k n} \nonumber \]

entonces

\ [\ begin {align}
\ frac {\ mathrm {d}} {\ mathrm {dn}} f [n] &=\ sum_ {k=0} ^ {N} c_ {k}\ frac {\ mathrm {d} e^ {j\ omega_0 k n}} {\ mathrm {dn}}\ nonumber\\
&=\ sum_ {k=0} ^ {N} c_ {k} j\ omega_ {0} k e^ {j\ omega_ {0} k n}
\ end {align}\ nonumber\]

Un diferenciador atenúa las frecuencias bajas\(f[n]\) y acentúa las frecuencias altas. Elimina tendencias generales y acentúa áreas de fuerte variación.

Nota

Una forma común de medir matemáticamente la suavidad de una función\(f[n]\) es ver cuántas derivadas son energía finita.

Esto se hace observando los coeficientes de Fourier de la señal, específicamente qué tan rápido decaen como\(k \rightarrow \infty\). Si\(\mathscr{F}(f[n])=c_{k}\) y\(|c_k|\) tiene la forma\(\frac{1}{k^l}\), entonces\(\mathscr{F}\left(\frac{\mathrm{d}^{m} f[n]}{\mathrm{d} n^{m}}\right)=\left(j k \omega_{0}\right)^{m} c_{k}\) y tiene la forma\(\frac{k^m}{k^l}\). Entonces, para que el derivado\(m\) ^th tenga energía finita, necesitamos

\[\sum_{k}\left(\left|\frac{k^{m}}{k^{l}}\right|\right)^{2}<\infty \nonumber \]

así\(\frac{k^{m}}{k^{l}}\) decae más rápido de\(\frac{1}{k}\) lo que implica que

\[2l - 2m > 1 \nonumber \]

o

\[l > \frac{2m+1}{2} \nonumber \]

Así, la tasa de decaimiento de la serie de Fourier dicta la suavidad.

Demostración de diferenciación de Fourier

Figura\(\PageIndex{3}\): Interactuar (cuando está en línea) con un CDF de Mathematica demostrando Diferenciación en un Dominio de Fourier. Para descargar, haga clic derecho y guárdalo como .cdf.

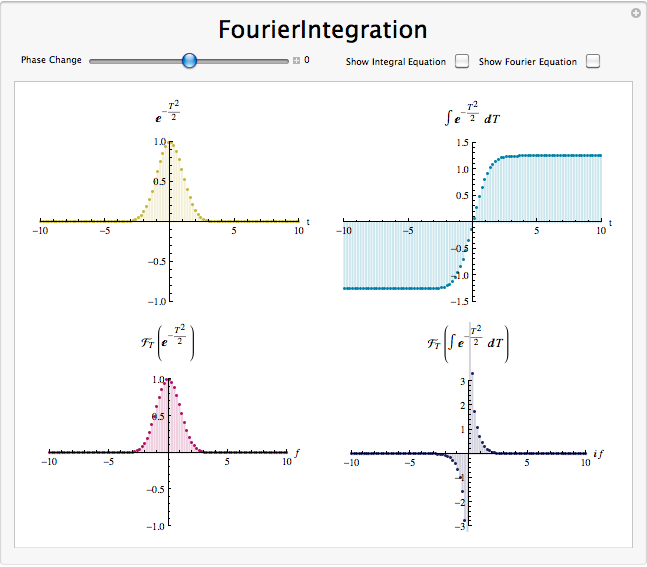
Integración en el dominio de Fourier

Si

\[\mathscr{F}(f[n])=c_{k} \nonumber \]

entonces

\[\mathscr{F}\left(\sum_{\eta=0}^{n} f[\eta]\right)=\frac{1}{j \omega_{0} k} c_{k} \nonumber \]

Nota

Si\(c_0 \neq 0\), esta expresión no tiene sentido.

La integración acentúa las bajas frecuencias y atenúa las frecuencias altas. Los integradores resaltan las tendencias generales en las señales y suprimen la variación a corto plazo (que en muchos casos es ruido). Los integradores son mucho más agradables que los diferenciadores.

Demostración de integración de Fourier

Figura\(\PageIndex{4}\): Interactuar (cuando esté en línea) con un CDF de Mathematica demostrando el efecto de la Integración en un Dominio de Fourier. Para descargar, haga clic derecho y guarde como .cdf.

Multiplicación de señal

Dada una señal\(f[n]\) con coeficientes de Fourier\(c_k\) y una señal\(g[n]\) con coeficientes de Fourier\(d_k\), podemos definir una nueva señal,\(y[n]\), donde\(y[n]=f[n]g[n]\). Encontramos que la representación de la Serie de Fourier de\(y[n]\)\(e_k\),, es tal que\(e_{k}=\sum_{l=0}^{N} c_{l} d_{k-l}\). Es decir que la multiplicación de la señal en el dominio del tiempo es equivalente a la convolución circular de tiempo discreto (Sección 4.3) en el dominio de la frecuencia. La prueba de ello es la siguiente

\ [\ begin {align}
e_ {k} &=\ frac {1} {N}\ suma_ {n=0} ^ {N} f [n] g [n] e^ {-\ izquierda (j\ omega_ {0} k n\ derecha)}\ nonumber\\
&=\ frac {1} {N}\ sum_ {n=0} ^ {N}\ sum_ {l=0} ^ {N} c_ {l} e^ {j\ omega_ {0} l n} g [n] e^ {-\ izquierda (j\ omega_ {0} k n\ derecha)}\ nonumber\\
&=\ suma_ {l=0} ^ {N} c_ {l}\ izquierda (\ frac {1} {N}\ suma_ {n=0} ^ {N} g [n] e^ {-\ izquierda (j\ omega_ {0} (k-l) n\ derecha)}\ derecha)\ nonumber\\
&=\ sum_ {l=0} ^ {N} c_ {l} d_ {k-l}
\ end {align}\ nonumber\]

Conclusión

Al igual que otras transformadas de Fourier, el DTFS tiene muchas propiedades útiles, incluyendo linealidad, igual energía en los dominios de tiempo y frecuencia, y análogos para desplazamiento, diferenciación e integración.

Tabla\(\PageIndex{1}\): Propiedades de la Transformada Discreta de Fourier

Propiedad	Señal	DTFS
Linealidad	\(ax(n)+by(n)\)	\(aX(k)+bY(k)\)
Cambio de tiempo	\(x(n−m)\)	\(X(k)e^{−j2 \pi mk/N}\)
Modulación de tiempo	\(x(n) e^{j 2 \pi m n / N}\)	\(X(k−m)\)
Multiplicación	\(x(n)y(n)\)	\(X(k)*Y(k)\)
Convolución Circular	\(x(n)*y(n)\)	\(X(k)Y(K)\)