7.4: Propiedades del DTFS
- Page ID
- 86499
Introducción
En este módulo discutiremos las propiedades básicas de la Serie de Fourier de Tiempo Discreto. Comenzaremos refrescando su memoria de nuestras ecuaciones básicas de la serie de Fourier:
\[f[n]=\sum_{k=0}^{N-1} c_{k} e^{j \omega_{0} k n} \nonumber \]
\[c_{k}=\frac{1}{\sqrt{N}} \sum_{n=0}^{N-1} f[n] e^{-\left(j \frac{2 \pi}{N} k n\right)} \nonumber \]
Dejar\(\mathscr{F}(\cdot)\) denotar la transformación de\(f[n]\) a los coeficientes de Fourier
\[\mathscr{F}(f[n])=c_{k} \quad, \quad k \in \mathbb{Z} \nonumber \]
\(\mathscr{F}(\cdot)\)mapea funciones complejas valoradas a secuencias de números complejos.
Linealidad
\(\mathscr{F}(\cdot)\)es una transformación lineal.
Teorema\(\PageIndex{1}\)
Si\(\mathscr{F}(f[n])=c_{k}\) y\(\mathscr{F}(g[n])=d_{k}\). Entonces
\[\mathscr{F}(\alpha f[n])=\alpha c_{k} \quad, \quad \alpha \in \mathbb{C} \nonumber \]
y
\[\mathscr{F}(f[n]+g[n])=c_{k}+d_{k} \nonumber \]
Prueba
Fácil. Justa linealidad de integral.
\ [\ begin {align}
\ mathscr {F} (f [n] +g [n]) &=\ sum_ {n=0} ^ {N} (f [n] +g [n]) e^ {-\ left (j\ omega_ {0} k n\ derecha)}, k\ in\ mathbb {Z}\ nonumber\\
&=\ frac {1} {N}\ suma_ {n=0} ^ {N} f [n] e^ {-\ izquierda (j\ omega_ {0} k n\ derecha)} +\ frac {1} {N}\ suma_ {n=0} ^ {N} g [n] e^ {-\ izquierda (j\ omega_ {0} k n\ derecha)}, k\ in \ mathbb {Z}\ nonumber\\
&=c_ {k} +d_ {k}, k\ in\ mathbb {Z}\ nonumber\\
&=c_ {k} +d_ {k}
\ end {align}\ nonumber\]
Desviación
El desplazamiento en el tiempo equivale a un desplazamiento de fase de los coeficientes de Fourier.
Teorema\(\PageIndex{2}\)
\(\mathscr{F}\left(f\left[n-n_{0}\right]\right)=e^{-\left(j \omega_{0} k n_{0}\right)} c_{k}\)si\(c_{k}=\left|c_{k}\right| e^{j \angle\left(c_{k}\right)}\), entonces
\[\left|e^{-\left(j \omega_{0} k n_{0}\right)} c_{k}\right|=\left|e^{-\left(j \omega_{0} k n_{0}\right)}\right|\left|c_{k}\right|=\left|c_{k}\right| \nonumber \]
\[ \angle\left(e^{-\left(j \omega_{0} n_{0} k\right)}\right)=\angle\left(c_{k}\right)-\omega_{0} n_{0} k \nonumber \]
Prueba
\ [\ begin {align}
\ mathscr {F}\ izquierda (f\ izquierda [n-n_ {0}\ derecha]\ derecha) &=\ frac {1} {N}\ suma_ {n=0} ^ {N} f\ izquierda [n-n_ {0}\ derecha] e^ {-\ izquierda (j\ omega_ {0} k n\ derecha)},\ k quad\ en\ mathbb {Z}\ nonumber\\
&=\ frac {1} {N}\ suma_ {n=-n_ {0}} ^ {n-n_ {0}} f\ izquierda [n-n_ {0}\ derecha] e^ {-\ izquierda (j\ omega_ {0} k\ izquierda (n-n_ {0}\ derecha)\ derecha)} e^ {-\ izquierda (j\ omega_ {0} k n_ {0}\ derecha)}\ quad,\ quad k\ in\ mathbb {Z}\ nonumber\\
&=\ frac {1} {N}\ sum_ {n=-n_ {0}} ^ {n-n_ {0}} [f\ tilde {n}] e^ {-\ izquierda (j\ omega_ {0} k\ tilde {n}\ derecha)} e^ {-\ izquierda (j\ omega_ {0} k n_ {0}\ derecha)}\ quad,\ quad k\ in\ mathbb {Z}\ nonumber\\
&=e^ {-\ izquierda (j\ omega_ {0} k\ tilde {n}\ derecha)} c_ {k}\ quad,\ quad k\ in\ mathbb {Z}
\ end {align}\ nonumber\]
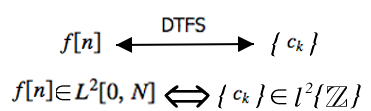
Relación de Parseval
\[ \sum_{n=0}^{N}(|f[n]|)^{2}=N \sum_{k=0}^{N-1}\left(\left|c_{k}\right|\right)^{2} \nonumber \]
La relación de Parseval nos dice que la energía de una señal es igual a la energía de su transformada de Fourier.
Nota
Parseval nos dice que la serie de Fourier se mapea\(L^2[0,N]\) a\(l^2\).
Figura\(\PageIndex{1}\)
Ejercicio\(\PageIndex{1}\)
\(f[n]\)Para tener “energía finita”, ¿cómo\(c_k\) hacen los\( k \rightarrow \infty\)?
- Contestar
-
\(\left(\left|c_{k}\right|\right)^{2}<\infty\)para\(f[n]\) tener energía finita.
Ejercicio\(\PageIndex{2}\)
Si\(\forall k,|k|>0:\left(c_{k}=\frac{1}{k}\right)\), ¿es\(f \in L^{2} [ [ 0, N ] ] \)?
- Contestar
-
Sí, porque\((|c_k|)^2=\frac{1}{k^2}\), que es sumable.
Ejercicio\(\PageIndex{3}\)
Ahora, si\(\forall k,|k|>0:\left(c_{k}=\frac{1}{\sqrt{k}}\right)\),\(f \in L^{2} [ [ 0, N ] ]\) ¿es?
- Contestar
-
No, porque\((|c_k|)^2=\frac{1}{k}\), que no es sumable.
La tasa de decaimiento de la serie de Fourier determina si\(f[n]\) tiene energía finita.
Demostración del Teorema de Parsevals
Propiedades de simetría
Regla\(\PageIndex{1}\): Even Signals
\(f[n] = f[-n]\)
\(\left\|c_{k}\right\|=\left\|c_{-k}\right\|\)
Prueba
\ (\ begin {align}
c_ {k} =&\ frac {1} {N}\ suma_ {0} ^ {N} [n]\ exp\ left [-j\ omega_ {0} k n\ derecha]\ nonumber\\
=&\ frac {1} {N}\ sum_ {0} ^ {\ frac {N} {2}} f [n]\ exp\ izquierda [-j\ omega_ {0} k n\ derecha] +\ frac {1} {N}\ suma_ {\ frac {N} {2}} ^ {N} f [n]\ exp\ izquierda [-j\ omega_ {0} k n\ derecha]\ nonumber\\
=&\ frac {1} {N}\ sum_ {0} ^ {\ frac {N} {2}} f [-n]\ exp\ left [-j\ omega_ {0} k n\ derecha] +\ frac {1} {N}\ sum_ {\ frac {N} {2}} ^ {N} f [-n]\ exp\ izquierda [-j\ omega_ {0} k n\ derecha]\ nonumber\\
=&\ frac {1} {N}\ suma_ {0} ^ {N} [n]\ izquierda [\ exp\ izquierda [j\ omega_ {0} k n\ derecha] +\ exp\ izquierda [-j\ omega_ {0} k n\ derecha]\ derecha]\ nonumber\\
=&\ frac {1} {N}\ suma_ {0} ^ {N} [n] 2\ cos\ izquierda [\ omega_ {0} k n\ derecha]
\ end {align}\)
Regla\(\PageIndex{2}\): Odd Signals
\(f[n]=-f[-n]\)
\(c_{k}=c_{-k}^*\)
Prueba
\ (\ begin {align}
c_ {k} =&\ frac {1} {N}\ sum_ {0} ^ {N} f [n]\ exp\ left [-\ mathrm {j}\ omega_ {0} k n\ derecha]\ nonumber\\
=&\ frac {1} {N}\ sum_ {0} ^ {\ frac {N} {2}} f [n]\ exp\ izquierda [-\ mathrm {j}\ omega_ {0} k n\ derecha] +\ frac {1} {N}\ sum_ {\ frac {N} {2}} ^ {N} f [n]\ exp\ left [-\ mathrm {j}\ omega_ {0} k n\ derecha]\ nonumber\\
=&\ frac {1} {N}\ suma_ {0} ^ {\ frac {N} {2}} f [n]\ exp\ izquierda [-\ mathrm {j}\ omega_ {0} k n\ derecha] -\ frac {1} {N} {N}\ sum_ {\ frac {N} {2} ^ {N} f [-n]\ exp\ izquierda [\ mathrm {j}\ omega_ {0} k n\ derecha]\ nonumber\\
=&-\ frac {1} {N}\ sum_ {0} ^ {N} f [n]\ left [\ exp\ left [\ mathrm {j}\ omega_ {0} k n\ derecha] -\ exp\ izquierda [-\ mathrm {j}\ omega_ {0} k n\ derecha]\ derecha]\ nonumber\\
=&-\ frac {1} {N}\ sum_ {0} ^ {N} f [n] 2\ nombreoperador {j\ sin}\ izquierda [\ omega_ {0} k n\ derecha]
\ end align {}\)
Regla\(\PageIndex{3}\): Real Signals
\(f[n] = f^*[n]\)
\(c_k = c_{-k}^*\)
Prueba
\ (\ displaystyle {\ begin {align}
c_ {k} =&\ frac {1} {N}\ sum_ {0} ^ {N} f [n]\ exp\ left [-\ mathrm {j}\ omega_ {0} k n\ derecha]\ nonumber\\
=&\ frac {1} {N}\ sum_ {0} ^ {\ frac N} {2}} f [n]\ exp\ izquierda [-\ mathrm {j}\ omega_ {0} k n\ derecha] +\ frac {1} {N} {N}\ sum_ {\ frac {N} {2}} ^ {N} f [n]\ exp\ left [-\ mathrm {j}\ omega_ {0} k n\ derecha]\ nonumber\\
=&\ frac {1} {N}\ suma_ {0} ^ {\ frac {N} {2}} f [-n]\ exp\ izquierda [-\ mathrm {j}\ omega_ {0} k n\ derecha] +\ frac {1} {N}\ n sum_ {\ frac {} {2}} ^ {N} f [-n]\ exp\ izquierda [-\ mathrm {j}\ omega_ {0} k n\ derecha]\ nonumber\\
=&\ frac {1} {N}\ sum_ {0} ^ {N} f [n]\ left [\ exp\ left [\ mathrm {j}\ omega_ {0} k n\ derecha] +\ exp\ izquierda [-\ mathrm {j}\ omega_ {0} k n\ derecha]\ derecha]\ nonumber\\
=&\ frac {1} {N}\ sum_ {0} ^ {N} f [n] 2\ cos\ izquierda [\ omega_ {0} k\ derecha]
\ final {align}}\)
Diferenciación en el Dominio de Fourier
\[\left(\mathscr{F}(f[n])=c_{k}\right) \Rightarrow\left(\mathscr{F}\left(\frac{\mathrm{d} f[n]}{\mathrm{d} n}\right)=j k \omega_{0} c_{k}\right) \nonumber \]
Desde
\[f[n]=\sum_{i=0}^{N} c_{k} e^{j \omega_{0} k n} \nonumber \]
entonces
\ [\ begin {align}
\ frac {\ mathrm {d}} {\ mathrm {dn}} f [n] &=\ sum_ {k=0} ^ {N} c_ {k}\ frac {\ mathrm {d} e^ {j\ omega_0 k n}} {\ mathrm {dn}}\ nonumber\\
&=\ sum_ {k=0} ^ {N} c_ {k} j\ omega_ {0} k e^ {j\ omega_ {0} k n}
\ end {align}\ nonumber\]
Un diferenciador atenúa las frecuencias bajas\(f[n]\) y acentúa las frecuencias altas. Elimina tendencias generales y acentúa áreas de fuerte variación.
Nota
Una forma común de medir matemáticamente la suavidad de una función\(f[n]\) es ver cuántas derivadas son energía finita.
Esto se hace observando los coeficientes de Fourier de la señal, específicamente qué tan rápido decaen como\(k \rightarrow \infty\). Si\(\mathscr{F}(f[n])=c_{k}\) y\(|c_k|\) tiene la forma\(\frac{1}{k^l}\), entonces\(\mathscr{F}\left(\frac{\mathrm{d}^{m} f[n]}{\mathrm{d} n^{m}}\right)=\left(j k \omega_{0}\right)^{m} c_{k}\) y tiene la forma\(\frac{k^m}{k^l}\). Entonces, para que el derivado\(m\) th tenga energía finita, necesitamos
\[\sum_{k}\left(\left|\frac{k^{m}}{k^{l}}\right|\right)^{2}<\infty \nonumber \]
así\(\frac{k^{m}}{k^{l}}\) decae más rápido de\(\frac{1}{k}\) lo que implica que
\[2l - 2m > 1 \nonumber \]
o
\[l > \frac{2m+1}{2} \nonumber \]
Así, la tasa de decaimiento de la serie de Fourier dicta la suavidad.
Demostración de diferenciación de Fourier
Integración en el dominio de Fourier
Si
\[\mathscr{F}(f[n])=c_{k} \nonumber \]
entonces
\[\mathscr{F}\left(\sum_{\eta=0}^{n} f[\eta]\right)=\frac{1}{j \omega_{0} k} c_{k} \nonumber \]
Nota
Si\(c_0 \neq 0\), esta expresión no tiene sentido.
La integración acentúa las bajas frecuencias y atenúa las frecuencias altas. Los integradores resaltan las tendencias generales en las señales y suprimen la variación a corto plazo (que en muchos casos es ruido). Los integradores son mucho más agradables que los diferenciadores.
Demostración de integración de Fourier
Multiplicación de señal
Dada una señal\(f[n]\) con coeficientes de Fourier\(c_k\) y una señal\(g[n]\) con coeficientes de Fourier\(d_k\), podemos definir una nueva señal,\(y[n]\), donde\(y[n]=f[n]g[n]\). Encontramos que la representación de la Serie de Fourier de\(y[n]\)\(e_k\),, es tal que\(e_{k}=\sum_{l=0}^{N} c_{l} d_{k-l}\). Es decir que la multiplicación de la señal en el dominio del tiempo es equivalente a la convolución circular de tiempo discreto (Sección 4.3) en el dominio de la frecuencia. La prueba de ello es la siguiente
\ [\ begin {align}
e_ {k} &=\ frac {1} {N}\ suma_ {n=0} ^ {N} f [n] g [n] e^ {-\ izquierda (j\ omega_ {0} k n\ derecha)}\ nonumber\\
&=\ frac {1} {N}\ sum_ {n=0} ^ {N}\ sum_ {l=0} ^ {N} c_ {l} e^ {j\ omega_ {0} l n} g [n] e^ {-\ izquierda (j\ omega_ {0} k n\ derecha)}\ nonumber\\
&=\ suma_ {l=0} ^ {N} c_ {l}\ izquierda (\ frac {1} {N}\ suma_ {n=0} ^ {N} g [n] e^ {-\ izquierda (j\ omega_ {0} (k-l) n\ derecha)}\ derecha)\ nonumber\\
&=\ sum_ {l=0} ^ {N} c_ {l} d_ {k-l}
\ end {align}\ nonumber\]
Conclusión
Al igual que otras transformadas de Fourier, el DTFS tiene muchas propiedades útiles, incluyendo linealidad, igual energía en los dominios de tiempo y frecuencia, y análogos para desplazamiento, diferenciación e integración.
| Propiedad | Señal | DTFS |
|---|---|---|
| Linealidad | \(ax(n)+by(n)\) | \(aX(k)+bY(k)\) |
| Cambio de tiempo | \(x(n−m)\) | \(X(k)e^{−j2 \pi mk/N}\) |
| Modulación de tiempo | \(x(n) e^{j 2 \pi m n / N}\) | \(X(k−m)\) |
| Multiplicación | \(x(n)y(n)\) | \(X(k)*Y(k)\) |
| Convolución Circular | \(x(n)*y(n)\) | \(X(k)Y(K)\) |


