1.1: Clasificaciones y propiedades de señales
- Page ID
- 86585
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Introducción
Este módulo iniciará nuestro estudio de señales y sistemas al exponer algunos de los fundamentos de la clasificación de señales. Se trata esencialmente de una introducción a las importantes definiciones y propiedades que son fundamentales para la discusión de señales y sistemas, con una breve discusión de cada uno.
Clasificaciones de señales
Tiempo Continuo vs Tiempo Discreto
Como sugieren los nombres, esta clasificación viene determinada por si el eje de tiempo es discreto (contable) o continuo (Figura\(\PageIndex{1}\)) o no. Una señal de tiempo continuo contendrá un valor para todos los números reales a lo largo del eje de tiempo. En contraste con esto, una señal de tiempo discreto, a menudo creada por muestreo de una señal continua, solo tendrá valores a intervalos igualmente espaciados a lo largo del eje de tiempo.
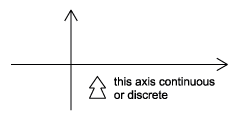
Figura\(\PageIndex{1}\)
Analógico vs. Digital
La diferencia entre analógico y digital es similar a la diferencia entre tiempo continuo y tiempo discreto. Sin embargo, en este caso la diferencia involucra los valores de la función. Analógico corresponde a un conjunto continuo de posibles valores de función, mientras que digital corresponde a un conjunto discreto de posibles valores de función. Un ejemplo común de una señal digital es una secuencia binaria, donde los valores de la función solo pueden ser uno o cero.
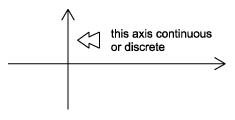
Figura\(\PageIndex{2}\)
Periódicos vs. Aperiódicos
Las señales periódicas se repiten con algún periodo\(T\), mientras que las señales aperiódicas, o no periódicas, no (Figura\(\PageIndex{3}\)). Podemos definir una función periódica a través de la siguiente expresión matemática, donde\(t\) puede ser cualquier número y\(T\) es una constante positiva:
\[f(t)=f(t+T) \label{1.1} \]
periodo fundamental de nuestra función,\(f(t)\), es el valor más pequeño de\(T\) que el todavia permite que la Ecuación\ ref {1.1} sea verdadera.
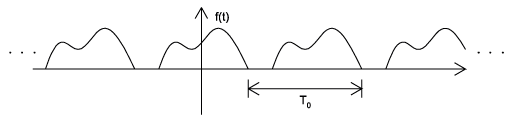
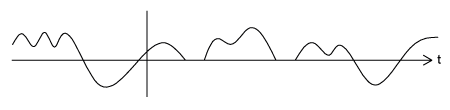 b)
b)
Longitud finita vs. Infinita
Otra forma de clasificar una señal es en términos de su longitud a lo largo de su eje de tiempo. ¿Se define la señal para todos los valores posibles de tiempo, o solo para ciertos valores de tiempo? Matemáticamente hablando,\(f(t)\) es una señal de longitud finita si se define solo sobre un intervalo finito
\[ t_{1}<t<t_{2} \nonumber \]
donde\(t_1 < t_2\). Del mismo modo, se define una señal de longitud infinita\(f(t)\),, para todos los valores:
\[ -\infty<t<\infty \nonumber \]
Causal vs. Anticausal vs No Causal
Las señales causales son señales que son cero para todo el tiempo negativo, mientras que anticausales son señales que son cero para todo tiempo positivo. Las señales no causales son señales que tienen valores distintos de cero tanto en tiempo positivo como negativo (Figura\(\PageIndex{4}\)).
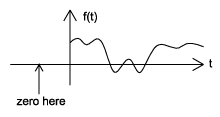 (a)
(a)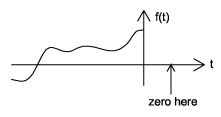 b)
b)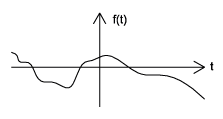 c)
c)
Par vs. Impar
Una señal par es cualquier señal\(f\) tal que\(f(t) = f(-t)\). Incluso las señales se pueden detectar fácilmente ya que son simétricas alrededor del eje vertical. Una señal impar, por otro lado, es una señal\(f\) tal que\(f(t)=−f(−t)\) (Figura\(\PageIndex{5}\)).
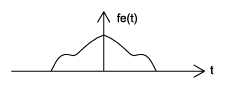 (a)
(a)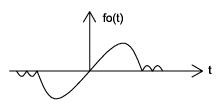 b)
b)
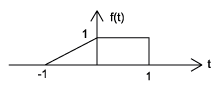
Usando las definiciones de señales pares e impares, podemos mostrar que cualquier señal puede escribirse como una combinación de una señal par e impar. Es decir, cada señal tiene una descomposición par-impar. Para demostrarlo, no hay que buscar más allá de una sola ecuación.
\[ f(t)=\frac{1}{2}(f(t)+f(-t))+\frac{1}{2}(f(t)-f(-t)) \label{1.2} \]
Al multiplicar y agregar esta expresión, se puede demostrar que es cierta. Además, se puede demostrar que\(f(t)+f(−t)\) cumple con el requisito de una función par, mientras que\(f(t)−f(−t)\) cumple con el requisito de una función impar (Figura\(\PageIndex{6}\)).
 (a)
(a)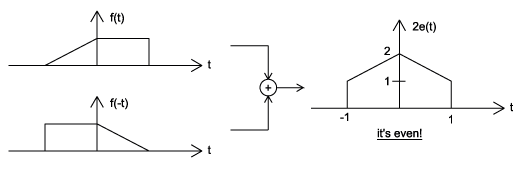 b)
b)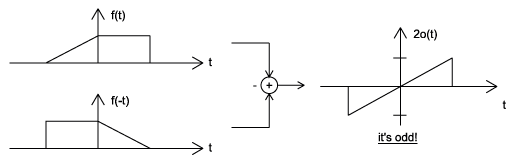 c)
c)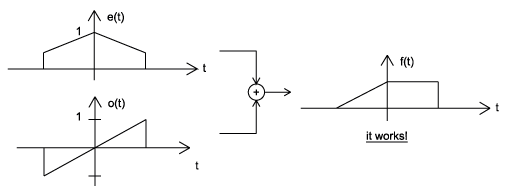 (d)
(d)
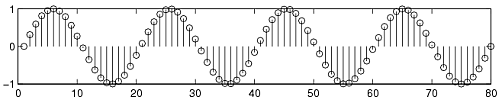
Determinístico vs Aleatorio
Una señal determinista es una señal en la que cada valor de la señal es fijo, siendo determinado por una expresión matemática, regla o tabla. Por otro lado, los valores de una señal aleatoria no están estrictamente definidos, sino que están sujetos a cierta cantidad de variabilidad.
 b)
b)
Considere la señal definida para todos los reales\(t\) descritos por
\ [f (t) =\ left\ {\ begin {array} {cc}
\ sin (2\ pi t)/t & t\ geq 1\\
0 & t<1
\ end {array}\ right. \ nonumber\]
Esta señal es de tiempo continuo, analógica, aperiódica, de longitud infinita, causal, ni par ni impar, y, por definición, determinista.
Resumen de clasificaciones de señales
Este módulo describe solo algunas de las muchas formas en que se pueden clasificar las señales. Pueden ser de tiempo continuo o tiempo discreto, analógicos o digitales, periódicos o aperiódicos, finitos o infinitos, y deterministas o aleatorios. También podemos dividirlos en función de sus propiedades de causalidad y simetría.


