1.8: Exponencial Complejo de Tiempo Continuo

Introducción

Los exponenciales complejos son algunas de las funciones más importantes en nuestro estudio de señales y sistemas. Su importancia se deriva de su condición de funciones propias de sistemas lineales invariantes en el tiempo. Antes de continuar, debes estar familiarizado con los números complejos.

El tiempo continuo complejo exponencial

Exponenciales Complejos

La compleja función exponencial se convertirá en una parte crítica de su estudio de señales y sistemas. Su forma general continua está escrita como

\[Ae^{st} \nonumber \]

donde\(s=\sigma+i \omega\) es un número complejo en términos de\(\sigma\), la constante de atenuación y\(\omega\) la frecuencia angular.

Fórmula de Euler

El matemático Euler demostró una identidad importante relacionando exponenciales complejos con funciones trigonométricas. Específicamente, descubrió la identidad epónimamente nombrada, la fórmula de Euler, que establece que

\[e^{j x}=\cos (x)+j \sin (x) \nonumber \]

que se puede probar de la siguiente manera.

Para probar la fórmula de Euler, comenzamos evaluando la serie Taylor para\(e^z\) aproximadamente\(z=0\), que converge para todos los complejos\(z\), en\(z=jx\). El resultado es

\ [\ begin {align}
e^ {j x} &=\ suma_ {k=0} ^ {\ infty}\ frac {(j x) ^ {k}} {k!} \ nonumber\\
&=\ suma_ {k=0} ^ {\ infty} (-1) ^ {k}\ frac {x^ {2 k}} {(2 k)!} +j\ sum_ {k=0} ^ {\ infty} (-1) ^ {k}\ frac {x^ {2 k+1}} {(2 k+1)!} \ nonumber\\
&=\ cos (x) +j\ sin (x)
\ end {align}\ nonumber\]

porque la segunda expresión contiene la serie Taylor for\(\cos(x)\) and\(\sin(x)\) about\(t=0\), que convergen para todos reales\(x\). Así, se prueba el resultado deseado.

Elegir\(x=\omega t\) esto da el resultado

\[e^{j \omega t}=\cos (\omega t)+j \sin (\omega t) \nonumber \]

que rompe un exponencial complejo temporal continuo en su parte real y parte imaginaria. Usando esta fórmula, también podemos derivar las siguientes relaciones.

\[\cos (\omega t)=\frac{1}{2} e^{j \omega t}+\frac{1}{2} e^{-j \omega t} \nonumber \]

\[\sin (\omega t)=\frac{1}{2 j} e^{j \omega t}-\frac{1}{2 j} e^{-j \omega t} \nonumber \]

Fasores de tiempo continuos

Se ha demostrado cómo lo exponencial complejo con frecuencia puramente imaginaria puede descomponerse en su parte real y su parte imaginaria. Consideremos ahora una frecuencia compleja general\(s=\sigma+\omega j\) donde\(\sigma\) está el factor de atenuación y\(\omega\) es la frecuencia. Considera también una diferencia de fase\(\theta\). De ello se deduce que

\[e^{(\sigma+j \omega) t+j \theta}=e^{\sigma t}(\cos (\omega t+\theta)+j \sin (\omega t+\theta)) \nonumber \]

Así, las partes reales e imaginarias de\(e^{st}\) aparecen a continuación.

\[\operatorname{Re}\left\{e^{(\sigma+j \omega) t+j \theta}\right\}=e^{\sigma t} \cos (\omega t+\theta) \nonumber \]

\[\operatorname{Im}\left\{e^{(\sigma+j \omega) t+j \theta}\right\}=e^{\sigma t} \sin (\omega t+\theta) \nonumber \]

Usar las partes reales o imaginarias de exponencial complejo para representar sinusoides con un retardo de fase multiplicado por exponencial real suele ser útil y se denomina notación fasora atenuada.

Podemos ver que tanto la parte real como la parte imaginaria tienen una sinusoide veces una exponencial real. También sabemos que los sinusoides oscilan entre uno y uno negativo. A partir de esto se hace evidente que las partes real e imaginaria del exponencial complejo oscilarán cada una dentro de una envolvente definida por la parte exponencial real.

(a)

b)

c)

Figura\(\PageIndex{1}\): Las formas posibles para la parte real de un exponencial complejo. Observe que las oscilaciones son el resultado de un coseno, ya que hay un máximo local en\(t=0\). (a) Si\(\sigma\) es negativo, tenemos el caso de una ventana exponencial en decadencia. (b) Si\(\sigma\) es positivo, tenemos el caso de una ventana exponencial creciente. (c) Si\(\sigma\) es cero, tenemos el caso de una ventana constante.

Demostración Exponencial Compleja

Figura\(\PageIndex{2}\): Interactuar (cuando esté en línea) con un CDF de Mathematica demostrando el Exponencial Complejo de Tiempo Continuo. Para Descargar, haga clic con el botón derecho y guarde el destino como .cdf.

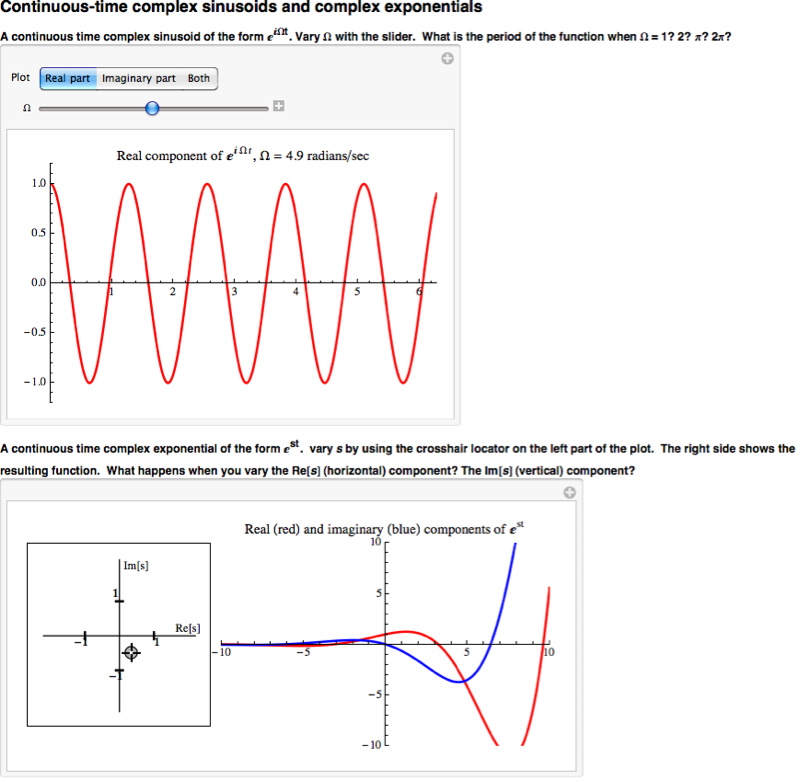
Resumen Exponencial Complejo de Tiempo Continuo

Los exponenciales complejos de tiempo continuo son señales de gran importancia para el estudio de señales y sistemas. Se pueden relacionar con sinusoides a través de la fórmula de Euler, que identifica las partes reales e imaginarias de exponenciales complejos puramente imaginarios. La fórmula de Eulers revela que, en general, las partes reales e imaginarias de exponenciales complejos son sinusoides multiplicados por exponenciales reales. Por lo tanto, la notación fasora atenuada suele ser útil para estudiar estas señales.