2.1: Clasificaciones y Propiedades del Sistema
- Page ID
- 86515
Introducción
En este módulo se introducirán brevemente algunas de las clasificaciones básicas de los sistemas y se explicarán las propiedades más importantes de estos sistemas. Como se puede ver, las propiedades de un sistema proporcionan una manera fácil de distinguir un sistema de otro. Comprender estas diferencias básicas entre los sistemas, y sus propiedades, será un concepto fundamental utilizado en todos los cursos de señales y sistemas. Una vez que un conjunto de sistemas puede identificarse como compartiendo propiedades particulares, ya no se tiene que reprobar una cierta característica de un sistema cada vez, sino que simplemente puede conocerse debido a la clasificación del sistema.
Clasificación de Sistemas
Continuo vs Discreto
Una de las distinciones más importantes a entender es la diferencia entre sistemas de tiempo discreto y continuo. Se dice que un sistema en el que la señal de entrada y la señal de salida tienen dominios continuos es un sistema continuo. Se dice que uno en el que la señal de entrada y la señal de salida tienen dominios discretos es un sistema discreto. Por supuesto, es posible concebir señales que no pertenezcan a ninguna categoría, como los sistemas en los que tenga lugar el muestreo de una señal de tiempo continua o la reconstrucción a partir de una señal de tiempo discreta.
Lineal vs. No lineal
Un sistema lineal es cualquier sistema que obedece a las propiedades de escalado (homogeneidad de primer orden) y superposición (aditividad) descritas más adelante. Un sistema no lineal es cualquier sistema que no tenga al menos una de estas propiedades.
Demostrar que un sistema\(H\) obedece a la propiedad de escalado es mostrar que
\[H(k f(t))=k H(f(t)) \nonumber \]
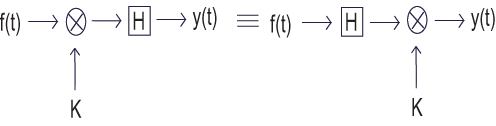
Demostrar que un sistema\(H\) obedece a la propiedad de superposición de linealidad es demostrar que
\[H\left(f_{1}(t)+f_{2}(t)\right)=H\left(f_{1}(t)\right)+H\left(f_{2}(t)\right) \nonumber \]
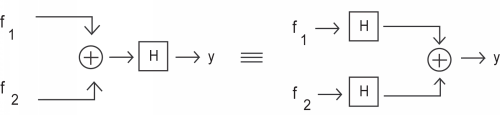
Es posible verificar la linealidad de un sistema en un solo paso (aunque más grande). Para ello, basta con combinar los dos primeros pasos para obtener
\[H\left(k_{1} f_{1}(t)+k_{2} f_{2}(t)\right)=k_{1} H\left(f_{1}(t)\right)+k_{2} H\left(f_{2}(t)\right) \nonumber \]
Invariante en el tiempo vs. variación en el tiempo
Se dice que un sistema es invariable en el tiempo si se conmuta con el parámetro shift operator definido por\(S_{T}(f(t))=f(t-T)\) for all\(T\), es decir
\[H S_{T}=S_{T} H \nonumber \]
para todos los reales\(T\). Intuitivamente, eso significa que para cualquier función de entrada que produzca alguna función de salida, cualquier cambio de tiempo de esa función de entrada producirá una función de salida idéntica en todos los sentidos excepto que se desplaza en la misma cantidad. Cualquier sistema que no tenga esta propiedad se dice que varía en el tiempo.
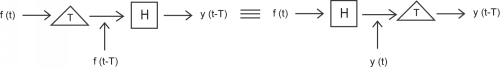
Causal vs. no causal
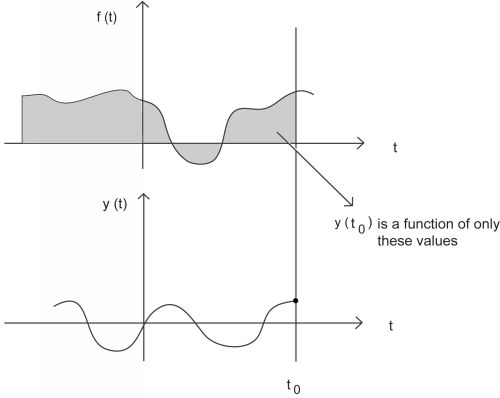
Un sistema causal es aquel en el que la salida depende únicamente de entradas actuales o pasadas, pero no de entradas futuras. De igual manera, un sistema anticausal es aquel en el que la salida depende únicamente de entradas actuales o futuras, pero no de entradas pasadas. Finalmente, un sistema no causal es aquel en el que la salida depende tanto de insumos pasados como futuros. Todos los sistemas “en tiempo real” deben ser causales, ya que no pueden tener insumos futuros disponibles para ellos.
Uno puede pensar que la idea de insumos futuros no parece tener mucho sentido físico; sin embargo, hasta ahora solo hemos estado tratando con el tiempo como nuestra variable dependiente, lo que no siempre es así. Imagina más bien que queríamos hacer procesamiento de imágenes. Entonces la variable dependiente podría representar posiciones de píxeles a la izquierda y derecha (el “futuro”) de la posición actual en la imagen, y no necesariamente tendríamos un sistema causal.

(a)
 b)
b)
Estable vs. Inestable
Existen varias definiciones de estabilidad, pero la que se utilizará con mayor frecuencia en este curso será la estabilidad de entrada acotada, salida acotada (BIBO). En este contexto, un sistema estable es aquel en el que la salida está delimitada si la entrada también está delimitada. De manera similar, un sistema inestable es aquel en el que al menos una entrada acotada produce una salida sin límites.
Representando esto matemáticamente, un sistema estable debe tener la siguiente propiedad, donde\(x(t)\) está la entrada y\(y(t)\) es la salida. La salida debe cumplir con la condición
\[|y(t)| \leq M_{y}<\infty \nonumber \]
siempre que tengamos una entrada al sistema que satisfaga
\[|x(t)| \leq M_{x}<\infty \nonumber \]
\(M_x\)y\(M_y\) ambos representan un conjunto de números positivos finitos y estas relaciones se mantienen para todos\(t\). De lo contrario, el sistema es inestable.
Resumen de Clasificaciones del Sistema
Este módulo describe solo algunas de las muchas formas en que se pueden clasificar los sistemas. Los sistemas pueden ser de tiempo continuo, tiempo discreto o ninguno. Pueden ser lineales o no lineales, invariables en el tiempo o variables en el tiempo, y estables o inestables. También podemos dividirlos en función de sus propiedades de causalidad. Existen otras formas de clasificar sistemas, como el uso de memoria, que no se discuten aquí sino que se describirán en módulos posteriores.


