2.2: Sistemas lineales invariantes en el tiempo
- Page ID
- 86516
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Introducción
La linealidad y la invarianza temporal son dos propiedades del sistema que simplifican enormemente el estudio de los sistemas que las exhiben. En nuestro estudio de señales y sistemas, estaremos especialmente interesados en sistemas que demuestren ambas propiedades, que en conjunto permitan el uso de algunas de las herramientas más potentes de procesamiento de señales.
Sistemas lineales invariantes en el tiempo
Sistemas Lineales
Si un sistema es lineal, esto significa que cuando una entrada a un sistema dado se escala por un valor, la salida del sistema se escala en la misma cantidad.
Escalado lineal
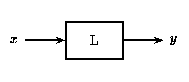 a)
a)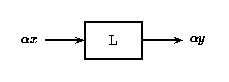 b)
b)
Figura\(\PageIndex{1}\)
En la Figura\(\PageIndex{1}\) (a) anterior, una entrada\(x\) al sistema lineal\(L\) da la salida\(y\). Si\(x\) se escala por un valor\(\alpha\) y se pasa a través de este mismo sistema, como en la Figura\(\PageIndex{1}\) (b), la salida también será escalada por\(\alpha\).
Un sistema lineal también obedece al principio de superposición. Esto significa que si se suman dos entradas y se pasan a través de un sistema lineal, la salida será la suma de las salidas de las entradas individuales.
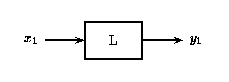 a)
a)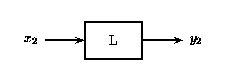 b)
b)
Figura\(\PageIndex{2}\)
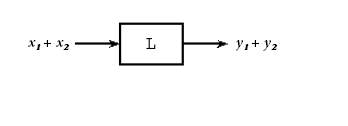
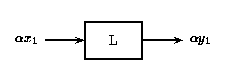
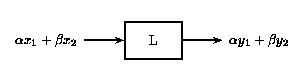
Es decir, si Figura\(\PageIndex{2}\) es verdadera, entonces Figura también\(\PageIndex{3}\) es verdadera para un sistema lineal. La propiedad de escalado mencionada anteriormente todavía se mantiene en conjunto con el principio de superposición. Por lo tanto, si las entradas x e y son escaladas por factores\(\alpha\) y\(\beta\), respectivamente, entonces la suma de estas entradas escaladas dará la suma de las salidas escaladas individuales:
 a)
a)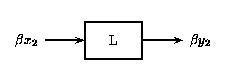 b)
b)
Figura\(\PageIndex{4}\)
Ejemplo\(\PageIndex{1}\)
Considera el sistema\(H_1\) en el que
\[H_{1}(f(t))=t f(t) \nonumber \]
para todas las señales\(f\). Dadas dos señales cualesquiera\(f\),\(g\) y escalares\(a\),\(b\)
\[\left.H_{1}(a f(t)+b g(t))\right)=t(a f(t)+b g(t))=atf(t)+b t g(t)=a H_{1}(f(t))+b H_{1}(g(t)) \nonumber \]
para todos reales\(t\). Así,\(H_1\) es un sistema lineal.
Ejemplo\(\PageIndex{2}\)
Considera el sistema\(H_2\) en el que
\[H_{2}(f(t))=(f(t))^{2} \nonumber \]
para todas las señales\(f\). Porque
\[H_{2}(2 t)=4 t^{2} \neq 2 t^{2}=2 H_{2}(t) \nonumber \]
para distinto de cero\(t\), no\(H_2\) es un sistema lineal.
Sistemas invariantes en el tiempo
Un sistema invariante en el tiempo tiene la propiedad de que una determinada entrada siempre dará la misma salida (hasta el momento), sin tener en cuenta cuándo se aplicó la entrada al sistema.
Sistemas invariantes en el tiempo
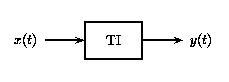 a)
a)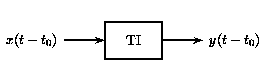 b)
b)En esta figura,\(x(t)\) y\(x(t−t_0)\) se pasan a través del sistema TI. Debido a que el sistema TI es invariable en el tiempo, las entradas\(x(t)\) y\(x(t−t_0)\) producen la misma salida. La única diferencia es que la salida debida a\(x(t−t_0)\) se desplaza por un tiempo\(t_0\).
Si un sistema es invariable en el tiempo o variable en el tiempo se puede ver en la ecuación diferencial (o ecuación de diferencia) que lo describe. Los sistemas invariantes en el tiempo se modelan con ecuaciones de coeficientes constantes. Una ecuación diferencial (o diferencia) de coeficiente constante significa que los parámetros del sistema no van cambiando con el tiempo y una entrada ahora dará el mismo resultado que la misma entrada más adelante.
Ejemplo\(\PageIndex{3}\)
Considera el sistema\(H_1\) en el que
\[H_{1}(f(t))=t f(t) \nonumber \]
para todas las señales\(f\). Porque
\[S_{T}\left(H_{1}(f(t))\right)=S_{T}(t f(t))=(t-T) f(t-T) \neq t f(t-T)=H_{1}(f(t-T))=H_{1}\left(S_{T}(f(t))\right) \nonumber \]
para distinto de cero\(T\), no\(H_1\) es un sistema invariante en el tiempo.
Ejemplo\(\PageIndex{4}\)
Considera el sistema\(H_2\) en el que
\[H_{2}(f(t))=(f(t))^{2} \nonumber \]
para todas las señales\(f\). Para todos los reales\(T\) y señales\(f\),
\[S_{T}\left(H_{2}(f(t))\right)=S_{T}\left(f(t)^{2}\right)=(f(t-T))^{2}=H_{2}(f(t-T))=H_{2}\left(S_{T}(f(t))\right) \nonumber \]
para todos reales\(t\). Así,\(H_2\) es un sistema invariante en el tiempo.
Sistemas lineales invariantes en el tiempo
Ciertos sistemas son tanto lineales como invariables en el tiempo, y por lo tanto se denominan sistemas LTI.
Sistemas lineales invariantes en el tiempo
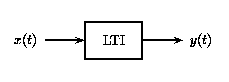 a)
a)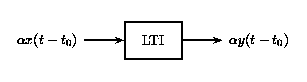 b)
b)Como los sistemas LTI son un subconjunto de sistemas lineales, obedecen al principio de superposición. En la siguiente figura, vemos el efecto de aplicar invarianza temporal a la definición de superposición en la sección de sistemas lineales anterior.
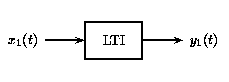 a)
a)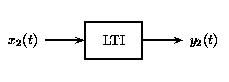 b)
b)
Figura\(\PageIndex{8}\)

Sistemas LTI en serie
Si dos o más sistemas LTI están en serie entre sí, su orden puede intercambiarse sin afectar la salida general del sistema. Los sistemas en serie también se denominan sistemas en cascada.
Sistemas LTI en cascada
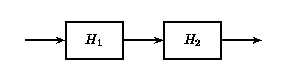 a)
a)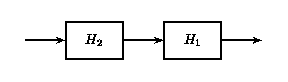 b)
b)Sistemas LTI en paralelo
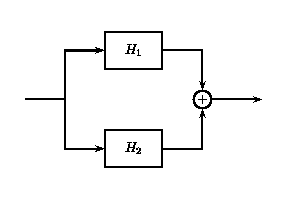
Si dos o más sistemas LTI están en paralelo entre sí, un sistema equivalente es uno que se define como la suma de estos sistemas individuales.
Sistemas LTI paralelos
 a)
a)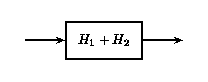 b)
b)Ejemplo\(\PageIndex{5}\)
Considera el sistema\(H_3\) en el que
\[H_{3}(f(t))=2 f(t) \nonumber \]
para todas las señales\(f\). Dadas dos señales cualesquiera\(f\),\(g\) y escalares\(a\),\(b\)
\[\left.H_{3}(a f(t)+b g(t))\right)=2(a f(t)+b g(t))=a 2 f(t)+b 2 g(t)=a H_{3}(f(t))+b H_{3}(g(t)) \nonumber \]
para todos reales\(t\). Así,\(H_3\) es un sistema lineal. Para todos los reales\(T\) y señales\(f\),
\[S_{T}\left(H_{3}(f(t))\right)=S_{T}(2 f(t))=2 f(t-T)=H_{3}(f(t-T))=H_{3}\left(S_{T}(f(t))\right) \nonumber \]
para todos reales\(t\). Así,\(H_3\) es un sistema invariante en el tiempo. Por lo tanto,\(H_3\) es un sistema lineal invariante en el tiempo.
Ejemplo\(\PageIndex{6}\)
Como se ha mostrado anteriormente, cada uno de los siguientes sistemas no son lineales o no invariables en el tiempo.
\[H_{1}(f(t))=t f(t) \nonumber \]
\[H_{2}(f(t))=(f(t))^{2} \nonumber \]
Por lo tanto, no son sistemas lineales invariantes en el tiempo.
Demostración lineal invariante en el tiempo
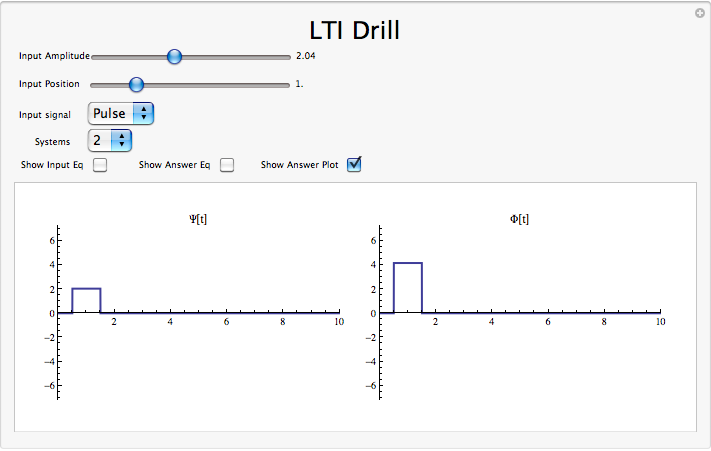
Resumen de sistemas LTI
Dos propiedades muy importantes y útiles de los sistemas acaban de ser descritas en detalle. El primero de ellos, la linealidad, nos permite saber que una suma de señales de entrada produce una señal de salida que es la suma de las señales de salida originales y que una señal de entrada escalada produce una señal de salida escalada a partir de la señal de salida original. El segundo de estos, la invarianza de tiempo, asegura que los turnos de tiempo conmuten con la aplicación del sistema. En otras palabras, la señal de salida para una entrada desplazada en el tiempo es la misma que la señal de salida para la señal de entrada original, excepto por un desplazamiento idéntico en el tiempo. Los sistemas que demuestran linealidad e invarianza temporal, a los que se les da el acrónimo sistemas LTI, son particularmente sencillos de estudiar ya que estas propiedades nos permiten aprovechar algunas de las herramientas más potentes en el procesamiento de señales.


