9.1: Señales Aperiódicas de Tiempo Discretas
- Page ID
- 86453
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
Introducción
Este módulo describe el tipo de señales sobre las que actúa la Transformada Discreta de Fourier de Tiempo.
Espacios Relevantes
La Transformada de Fourier de Tiempo\(l^2(\mathbb{Z})\) Discreto mapea señales de tiempo discretas arbitrarias en señales de frecuencia discreta de longitud finita en\(L^2([0,2 \pi))\).
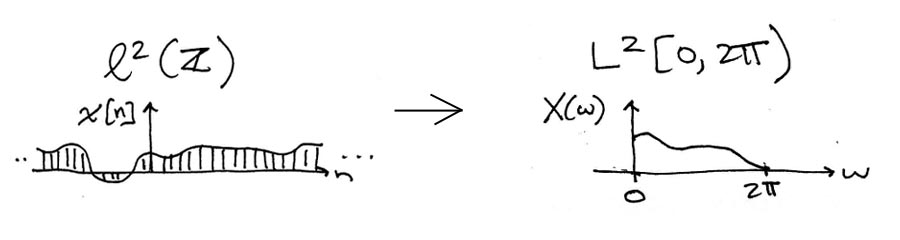
Señales Periódicas y Aperiódicas
Cuando una función se repite exactamente después de algún periodo, o ciclo dado, decimos que es periódica. Una función periódica puede definirse matemáticamente como:
\[f[n]=f[n+m N] \quad m \in \mathbb{Z} \label{9.1} \]
donde\(N > 0\) representa el periodo fundamental de la señal, que es el valor positivo más pequeño de N para que la señal se repita. Debido a esto, es posible que también vea una señal denominada señal N-periódica. Se dice que cualquier función que satisfaga esta ecuación es periódica con el periodo N. Las señales periódicas en tiempo discreto se repiten en cada ciclo. Sin embargo, solo se permiten números enteros como variables de tiempo en tiempo discreto. Denotamos señales en tal caso como\(f[n]\),\(n = ..., -2, -1, 0, 1, 2, ...\) Aquí hay un ejemplo de una señal periódica de tiempo discreto con periodo N:
Podemos pensar en funciones periódicas (con punto\(N\)) de dos maneras diferentes:
- como funciones en todos\(\mathbb{R}\)
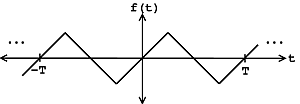
Figura\(\PageIndex{3}\): función periódica de tiempo discreto sobre todo\(\mathbb{R}\) donde\(f[n_0]=f[n_0+N]\) - o, podemos cortar toda la redundancia, y pensar en ellas como funciones en un intervalo\([0,N]\) (o, más generalmente,\([a,a+N]\). Si sabemos que la señal es N-periódica entonces toda la información de la señal es capturada por el intervalo anterior.
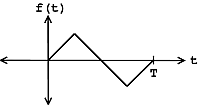
Figura\(\PageIndex{4}\): Eliminar la redundancia de la función period para que\(f[n]\) quede indefinida afuera\([0,N]\).
Una función DT aperiódica, sin embargo,\(f[n]\) no se repite para ninguna\(N \in \mathbb{R}\); es decir, no existe\(N\) tal que la Ecuación\ ref {9.1} mantenga. Esta clase más amplia de señales solo puede ser actuada por el DTFT.
Supongamos que tenemos tal función aperiódica\(f[n]\). Podemos construir una extensión periódica de\(f[n]\) llamada\(f_{No}[n]\), donde\(f[n]\) se repite cada\(N_0\) segundo. Si tomamos el límite como\(N_{0} \rightarrow \infty\), obtenemos un modelo preciso de una señal aperiódica para la que se pueden aplicar todas las reglas que gobiernan las señales periódicas, incluido el Análisis de Fourier (con una modificación importante). Para más detalles sobre esta distinción, consulte el módulo en la Transformada de Fourier de Tiempo de Discete.
Demostración de señal aperiódica
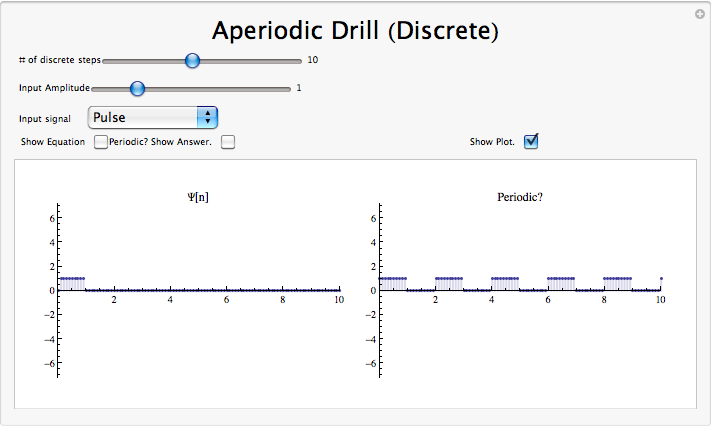
Conclusión
Una señal periódica discreta está completamente definida por sus valores en un periodo, como el intervalo [0, N]. Cualquier señal aperiódica puede definirse como una suma infinita de funciones periódicas, una definición útil que permite usar Análisis de Fourier en ella asumiendo que todas las frecuencias están presentes en la señal.


