9.2: Transformada Discreta de Fourier de Tiempo (DTFT)
- Page ID
- 86474
Introducción
En este módulo, derivaremos una expansión para funciones arbitrarias de tiempo discreto y, al hacerlo, derivaremos la Transformada Discreta de Fourier de Tiempo (DTFT).
Dado que los exponenciales complejos (Sección 1.8) son funciones propias de sistemas lineales invariantes en el tiempo (LTI) (Sección 14.5), calcular la salida de un sistema LTI\(\mathcal{H}\) dado\(e^{j \omega n}\) como entrada equivale a multiplicación simple\(\omega_{0}=\frac{2 \pi k}{N}\), dónde y dónde\(H[k] \in \mathrm{C}\) está el valor propio correspondiente a \(k\). Como se muestra en la figura, una entrada exponencial simple produciría la salida
\[y[n]=H[k] e^{j \omega n} \nonumber \]
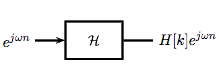
Usando esto y el hecho de que\(\mathcal{H}\) es lineal, calcular\(y[n]\) para combinaciones de exponenciales complejos también es sencillo.
\ [\ begin {array} {c}
c_ {1} e^ {j\ omega_ {1} n} +c_ {2} e^ {j\ omega_ {2} n}\ fila derecha c_ {1} H\ izquierda [k_ {1}\ derecha] e^ {j\ omega_ {1} n} +c_ {2} H\ izquierda [k_ {2}\ derecha] e^ {j\ omega_ {1} n}\
\ suma_ {l} c_ {l} e^ {j\ omega_ {l} n}\ fila derecha\ suma_ {l} c_ {l} H\ izquierda [k_ {l}\ derecha] e^ {j\ omega_ {l} n}
\ end {array}\ nonumber\]
La acción de\(H\) sobre una entrada como las de las dos ecuaciones anteriores es fácil de explicar. \(\mathbf{\mathcal{H}}\)escala independientemente cada componente exponencial\(e^{j \omega_{l} n}\) por un número complejo diferente\(H\left[k_{l}\right] \in \mathbb{C}\). Como tal, si podemos escribir una función\(y[n]\) como una combinación de exponenciales complejos nos permite calcular fácilmente la salida de un sistema.
Ahora, buscaremos usar el poder de exponenciales complejos para ver cómo podemos representar señales arbitrarias en términos de un conjunto de funciones más simples por superposición de una serie de exponenciales complejos. A continuación presentaremos la Transformada de Fourier en Tiempo Discreto (DTFT). Debido a que el DTFT se ocupa de las señales no periódicas, debemos encontrar la manera de incluir todas las frecuencias reales en las ecuaciones generales. Para el DTFT simplemente utilizamos la suma sobre todos los números reales en lugar de la suma sobre números enteros para expresar las señales aperiódicas.
Síntesis de DTFT
Se puede demostrar que una función arbitraria de tiempo periódico discreto\(f[n]\) puede escribirse como una combinación lineal de sinusoides complejos armónicos
\[f[n]=\sum_{k=0}^{N-1} c_{k} e^{j \omega_{0} k n} \label{9.3} \]
donde\(\omega_{0}=\frac{2 \pi}{N}\) está la frecuencia fundamental. Para casi todos los\(f[n]\) de interés práctico, existe\(c_n\) para hacer verdadera la Ecuación\ ref {9.3}. Si\(f[n]\) es energía finita (\(f[n] \in L^{2}[0, N]\)), entonces la igualdad en la Ecuación\ ref {9.3} se mantiene en el sentido de convergencia de energía; con señales de tiempo discreto, no hay preocupaciones por la divergencia como hay con las señales de tiempo continuo.
Los\(c_n\) -llamados coeficientes de Fourier- nos dicen “cuánto” de la sinusoide\(e^{j \omega_{0} kn}\) se encuentra en\(f[n]\). La fórmula\(f[n]\) se muestra como una suma de exponenciales complejos, cada uno de los cuales es fácilmente procesado por un sistema LTI (ya que es una función propia de cada sistema LTI). Matemáticamente, nos dice que el conjunto de exponenciales complejos\(\left\{e^{j \omega_{0} k n}, k \in \mathbb{Z}\right\}\) forman una base para el espacio de N-funciones de tiempo discretas periódicas.
Ecuaciones
Ahora bien, para tomar esta útil herramienta y aplicarla a señales arbitrarias no periódicas, tendremos que profundizar en el uso del principio de superposición. Dejar\(s_T(t)\) ser una señal periódica teniendo periodo\(T\). Queremos considerar qué sucede con el espectro de esta señal a medida que el periodo va hasta el infinito. Denotamos el espectro para cualquier valor supuesto del periodo por\(c_n(T)\). Calculamos el espectro de acuerdo con la fórmula de Fourier para una señal periódica, conocida como la Serie de Fourier (para más información sobre esta derivación, consulte la sección sobre Serie de Fourier.)
\[c_{n}=\frac{1}{T} \int_{0}^{T} s(t) \exp \left(-j \omega_{0} t\right) d t \nonumber \]
donde\(\omega_0 = \frac{2 \pi}{T}\) y donde hemos utilizado una colocación simétrica del intervalo de integración sobre el origen para su posterior conveniencia derivacional. Variamos el índice de frecuencia\(n\) proporcionalmente a medida que aumentamos el periodo. Definir
\[S_{T}(f) \equiv T c_{n}=\frac{1}{T} \int_{0}^{T} S_{T}(f) \exp \left(j \omega_{0} t\right) d t \nonumber \]
haciendo la serie de Fourier correspondiente
\[s_{T}(t)=\sum_{-\infty}^{\infty} f(t) \exp \left(j \omega_{0} t\right) \frac{1}{T} \nonumber \]
A medida que aumenta el período, las líneas espectrales se acercan, convirtiéndose en un continuo. Por lo tanto,
\[\lim _{T \rightarrow \infty} s_{T}(t) \equiv s(t)=\int_{-\infty}^{\infty} S(f) \exp \left(j \omega_{0} t\right) d f \nonumber \]
con
\[S(f)=\int_{-\infty}^{\infty} s(t) \exp \left(-j \omega_{0} t\right) d t \nonumber \]
Transformada de Fourier en Tiempo Discreto
\[\mathcal{F}(\omega)=\sum_{n=-\infty}^{\infty} f[n] e^{-(j \omega n)} \nonumber \]
Inverso DTFT
\[f[n]=\frac{1}{2 \pi} \int_{-\pi}^{\pi} \mathcal{F}(\omega) e^{j \omega n} d \omega \nonumber \]
Advertencia
No es raro ver la fórmula anterior escrita ligeramente diferente. Una de las diferencias más comunes es la forma en que se escribe lo exponencial. Las ecuaciones anteriores utilizan la variable de frecuencia radial\(\omega\) en el exponencial\(\omega = 2 \pi f\), donde, pero también es común incluir la expresión más explícita,\(j 2 \pi f t\), en la exponencial. En ocasiones la notación DTFT se expresa como\(F(e^{j \omega})\), para dejar claro que no se trata de un CTFT (que se denota como\(F(\Omega)\). Haga clic aquí para obtener una descripción general de la notación utilizada en los módulos DSP de Connexion.
Demostración de definición DTFT
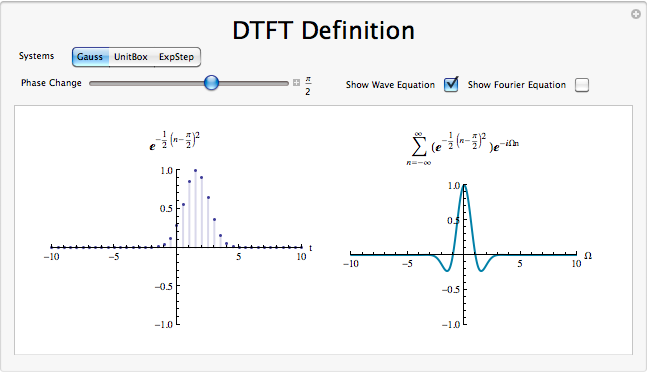
Resumen de DTFT
Debido a que los exponenciales complejos son funciones propias de los sistemas LTI, a menudo es útil representar señales usando un conjunto de exponenciales complejos como base. La fórmula de síntesis de transformada de Fourier de tiempo discreto expresa una función aperiódica de tiempo discreto como la suma infinita de exponenciales complejos de frecuencia continua.
\[\mathcal{F}(\omega)=\sum_{n=-\infty}^{\infty} f[n] e^{-(j \omega n)} \nonumber \]
La fórmula de análisis de transformada de Fourier de tiempo discreto toma la misma señal discreta en el dominio del tiempo y representa la señal en el dominio de frecuencia continua.
\[f[n]=\frac{1}{2 \pi} \int_{-\pi}^{\pi} \mathcal{F}(\omega) e^{j \omega n} d \omega \nonumber \]


