1.4: Flujo y divergencia

Si medimos la masa total de fluido que ingresa al volumen en la Figura 1-13 y encontramos que es menor que la masa que sale, sabemos que debe haber una fuente adicional de fluido dentro de la tubería. Si la masa que sale es menor que la que entra, entonces

Figura 1-13 El flujo neto a través de una superficie cerrada nos indica si hay una fuente o sumidero dentro de un volumen cerrado.

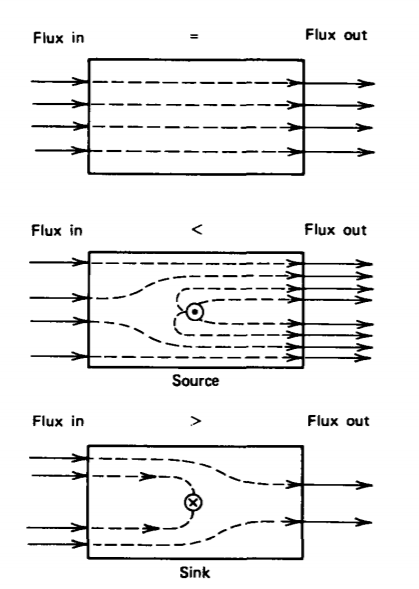
hay un fregadero (o drenaje) dentro del volumen. En ausencia de fuentes o sumideros, la masa de fluido que sale es igual a la que entra por lo que las líneas de flujo son continuas. Las líneas de flujo se originan en una fuente y terminan en un sumidero.

Flux

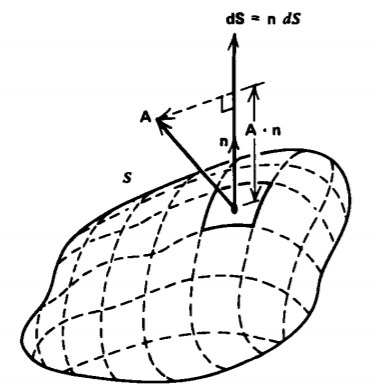
Estamos ilustrando con una analogía fluida lo que se llama el flujo (\(\Phi\)de un vector A a través de una superficie cerrada:

\[\Phi = \oint_{S}A \cdot \bf{dS} \nonumber \]

El elemento superficial diferencial dS es un vector que tiene una magnitud igual a un área incremental en la superficie pero apunta en la dirección de la unidad saliente normal n a la superficie S, como en la Figura 1-14. Solo el componente de A perpendicular a la superficie contribuye al flujo, ya que el componente tangencial solo da como resultado el flujo del vector A a lo largo de la superficie y no a través de ella. Una contribución positiva al flujo ocurre si A tiene un componente en la dirección de dS fuera de la superficie. Si el componente normal de A apunta en el volumen, tenemos una contribución negativa al flujo.

Si no hay fuente para A dentro del volumen V encerrado por la superficie S, todo el flujo que ingresa al volumen equivale a esa salida y el flujo neto es cero. Una fuente de A dentro del volumen genera más flujo saliendo que entrando para que el flujo sea positivo (\(\Phi\)>0) mientras que un sumidero tiene más flujo entrando que saliendo de manera que (\(\Phi\)< 0.)

Figura 1-14 El flujo de un vector A a través de la superficie cerrada S viene dado por la integral superficial del componente de A perpendicular a la superficie S. El elemento de área superficial vectorial diferencial dS está en la dirección de la unidad normal n.

Así vemos que el signo y magnitud del flujo neto relaciona la cantidad de un campo a través de una superficie con las fuentes o sumideros del campo vectorial dentro del volumen cerrado.

Divergencia

Podemos ser más explícitos sobre la relación entre la tasa de cambio de un campo vectorial y sus fuentes aplicando (1) a un volumen de tamaño diferencial, que por simplicidad tomamos como rectangular en la Figura 1-15. Hay tres pares de superficies planas paralelas perpendiculares a los ejes de coordenadas de manera que (1) da el flujo como

\[\Phi = \int_{1} A_{x}(x) dy dz = \int_{1'} A_{x}(x- \Delta x) dy dz + \int_{2}A_{y} (y + \Delta y) dx dz - \int_{2'} A_{y}(y) dx dz + \int_{3}A_{z}(z + \Delta z) dx dy - \int_{3'} A_{z}(z) dx dy \nonumber \]

donde las superficies imprimadas son distancias diferenciales detrás de las superficies no imprimadas correspondientes. Los signos menos surgen porque las normales salientes en las superficies imprimadas apuntan en las direcciones de coordenadas negativas.

Debido a que las superficies son de tamaño diferencial, los componentes de A son aproximadamente constantes a lo largo de cada superficie de modo que las integrales superficiales en (2) se vuelven puras

Figura 1-15 Volumen rectangular infinitesimal utilizado para definir la divergencia de un vector.

multiplicaciones del componente de A perpendicular a la superficie y al área superficial. El flujo luego se reduce a la forma

\[\Phi \approx (\frac{[A_{x}(x) - A_{x}(x- \Delta x)]}{\Delta x} + \frac{[A_{y} (y + \Delta y) - A_{y} (y)]}{\Delta y} + \frac{[A_{z}(z + \Delta z) - A_{z} (z)]}{\Delta z}) \Delta x \Delta y \Delta x \nonumber \]

Hemos escrito (3) en esta forma para que en el límite a medida que el volumen se vuelve infinitesimalmente pequeño, cada uno de los términos entre corchetes define una derivada parcial

\[\lim_{\Delta x \rightarrow 0 \\ \Delta y \rightarrow 0 \\ \Delta z \rightarrow 0} \Phi = (\frac{\partial A_{x}}{\partial x} + \frac{\partial A_{y}}{\partial y} + \frac{\partial A_{z}}{\partial z}) \Delta V \nonumber \]

donde\(\Delta V = \Delta x \Delta y \Delta x\) está el volumen encerrado por la superficie S.

El coeficiente de\(\Delta V\) in (4) es un escalar y se denomina divergencia de A. Se puede reconocer como el producto puntual entre el vector del operador de la Sección 1-3-1 y el vector A:

\[\textrm{div} \: \textbf{A} = \nabla \cdot \textbf{A} = \frac{\partial A_{x}}{\partial x} + \frac{\partial A_{y}}{\partial y} + \frac{\partial A_{z}}{\partial z} \nonumber \]

Coordenadas curvilíneas

En coordenadas cilíndricas y esféricas, la operación de divergencia no es simplemente el producto puntual entre un vector y el operador del porque las direcciones de los vectores unitarios son una función de las coordenadas. Así, las derivadas de los vectores unitarios tienen contribuciones distintas de cero. Es más fácil utilizar la definición generalizada de la divergencia independiente del sistema de coordenadas, obtenida de (1) - (5) como

\[\nabla \cdot A = \lim_{\Delta V \rightarrow 0} \frac{\oint_{S} \textbf{A} \cdot \textbf{dS}}{\Delta V} \nonumber \]

(a) Coordenadas Cilíndricas

En coordenadas cilíndricas utilizamos el pequeño volumen mostrado en la Figura 1-16 a para evaluar el flujo neto como

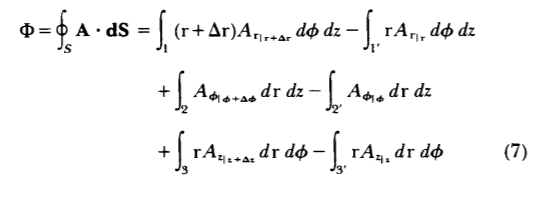
\[\Phi = \oint_{S} \textbf{A} \cdot \textbf{dS} = \int_{1} (\textrm{r} + \Delta \textrm{r}) A_{\textrm{r}_{\mid_{\textrm{r} + \Delta \textrm{r}}}} d \phi dz - \int_{1'} \textrm{r} A_{\textrm{r}_{\mid_{\textrm{r}}}} d \phi dz + \int_{2} A _{\phi_{\mid \phi + \Delta \phi}} d \textrm{r}\: dz - \int_{2'} A_{\phi_{\mid \phi}} d \textrm{r} dz + \int_{3} \textrm{r} A_{z_{\mid z + \Delta z}} d \textrm{r} d \phi - \int_{3'} \textrm{r} A_{z_{\mid_{z}}} d \textrm{r} d \phi \nonumber \]

Figura 1-16 Volúmenes infinitesimales utilizados para definir la divergencia de un vector en (a) geometrías cilíndricas y (b) esféricas.

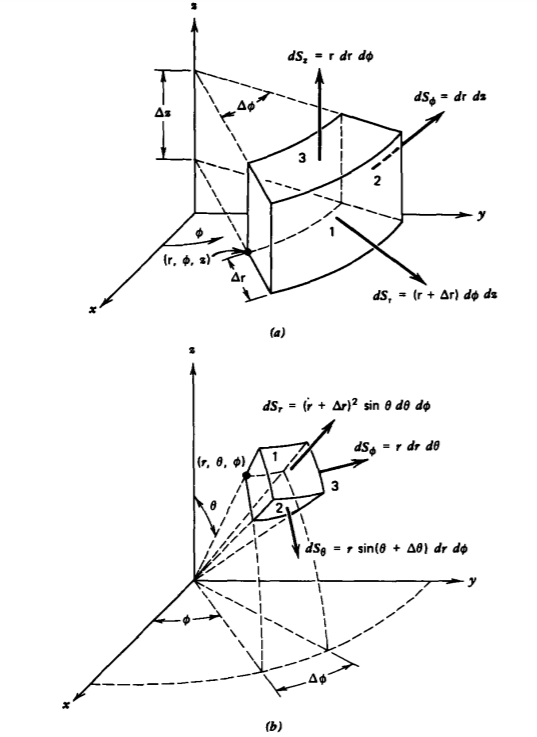
Nuevamente, debido a que el volumen es pequeño, podemos tratarlo como aproximadamente rectangular con los componentes de A aproximadamente constantes a lo largo de cada cara. Luego factorizando el volumen\(\Delta V = \textrm{r} \Delta \textrm{r} \Delta \phi \Delta z\) en (7),

\[\Phi \approx (\frac{[(r + \Delta r) A_{r_{\mid \textrm{r} + \Delta \textrm{r}}} -\textrm{r} A_{\textrm{r}_{\mid \textrm{r}}}]}{\textrm{r} \Delta \textrm{r}} + \frac{[A_{\phi_{\mid \phi + \Delta \phi}} - A_{\phi_{\mid_{\phi}}}]}{\textrm{r} \Delta \phi} + \frac{[A_{z_{\mid z + \Delta z}} - A_{z_{\mid z}}]}{\Delta z}) \textrm{r} \Delta \textrm{r} \: \Delta \phi \: \Delta z \nonumber \]

permite que cada uno de los términos entre corchetes se convierta en una derivada parcial a medida que las longitudes diferenciales se acercan a cero y (8) se convierte en La divergencia es entonces

\[\nabla \cdot \textbf{A} = \lim_{\Delta \textrm{r} \rightarrow 0 \\ \Delta \phi \rightarrow 0 \\ \Delta x \rightarrow 0} \: \frac{\oint_{S} \textbf{A} \cdot \textbf{dS}}{\Delta V} =\frac{1}{\textrm{r}} \frac{\partial}{\partial \textrm{r}} (\textrm{r} A_{\textrm{r}}) + \frac{1}{\textrm{r}} \frac{\partial A_{\phi}}{\partial \phi} + \frac{\partial A_{z}}{\partial z} \nonumber \]

(b) Coordenadas esféricas

Operaciones similares en el elemento de volumen esférico\(\Delta V = r^{2} \sin \: \theta \: \Delta r \: \Delta \theta \: \Delta \phi\) en la Figura 1-16 b definen el flujo neto a través de las superficies:

\[\Phi = \oint_{2} \textbf{A} \cdot \textbf{dS} \approx (\frac{[(r + \Delta r)^{2} A_{r_{\mid r + \Delta r}} -r^{2}A_{r_{\mid r}}]}{r^{2} \Delta r} + \frac{[A_{\theta_{\mid \theta + \Delta \theta}} \sin \: (\theta + \Delta \theta) - A_{\theta_{\mid \theta}} \: \sin \theta]}{r \: \sin \: \theta \: \Delta \theta} + \frac{[A_{\phi_{\mid \phi + \Delta \phi}} - A_{\phi_{\mid \phi}}]}{r \: \sin \: \theta \: \Delta \phi}) r^{2} \: \sin \theta \: \Delta r \: \Delta \theta \: \Delta \phi \nonumber \]

La divergencia en las coordenadas esféricas es entonces

\[\nabla \cdot \textbf{A} = \lim_{\Delta r \rightarrow 0 \\ \Delta \theta \rightarrow 0 \\ \Delta \phi \rightarrow 0} \frac{\oint_{S} \textbf{A} \cdot \textbf{dS}}{\Delta V} = \frac{1}{r^{2}} \frac{\partial}{\partial r} (r^{2} A_{r}) + \frac{1}{r \: \sin \theta} \frac{\partial}{\partial \theta}(A_{\theta} \sin \: \theta) + \frac{1}{r \: \sin \: \theta} \frac{\partial A_{\partial}}{\partial \phi} \nonumber \]

Teorema de Divergencia

Si ahora tomamos muchos volúmenes incrementales contiguos de cualquier forma, formamos un volumen macroscópico V con la superficie envolvente S como se muestra en la Figura 1-17 a. Sin embargo, cada superficie común interior entre volúmenes incrementales tiene el flujo que sale de un volumen (contribución de flujo positivo) justo entrando al volumen adyacente (contribución de flujo negativo) como en la Figura 1-17 b. La contribución neta al flujo para la integral superficial de (1) es cero para todas las superficies interiores. Las contribuciones distintas de cero al flujo se obtienen solo para aquellas superficies que unen la superficie externa S de V. Aunque las contribuciones superficiales al flujo usando (1) cancelan para todos los volúmenes interiores, el flujo obtenido de (4) en términos de la operación de divergencia para

Figura 1-17 Las contribuciones distintas de cero al flujo de un vector solo se obtienen a través de aquellas superficies que unen el exterior de un volumen. (a) Dentro del volumen el flujo que sale de un volumen incremental simplemente ingresa al volumen adyacente donde (b) las normales salientes a la superficie común que separan los volúmenes están en direcciones opuestas.

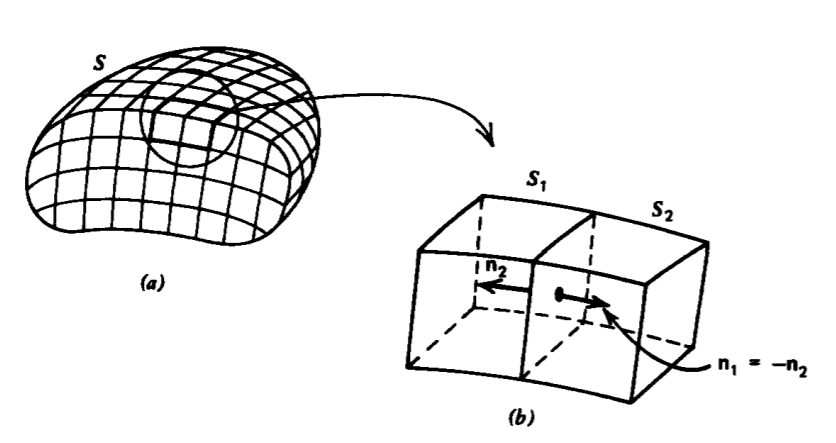
cada agregado de volumen incremental. Al sumar todas las contribuciones de cada volumen diferencial, obtenemos el teorema de la divergencia:

\[\Phi = \oint_{S} \textbf{A} \cdot \textbf{dS} = \lim_{N \rightarrow \infty \\ \Delta V_{n} \rightarrow 0} \sum_{n=1}^{\infty} (\nabla \cdot \textbf{A}) \Delta V_{n} = \int_{V} \nabla \cdot \textbf{A} dV \nonumber \]

donde el volumen V puede ser de tamaño macroscópico y está encerrado por la superficie externa S. Este poderoso teorema convierte una integral de superficie en una integral de volumen equivalente y se utilizará muchas veces en nuestro desarrollo de la teoría del campo electromagnético.

Ejemplo 1-6: El teorema de la divergencia

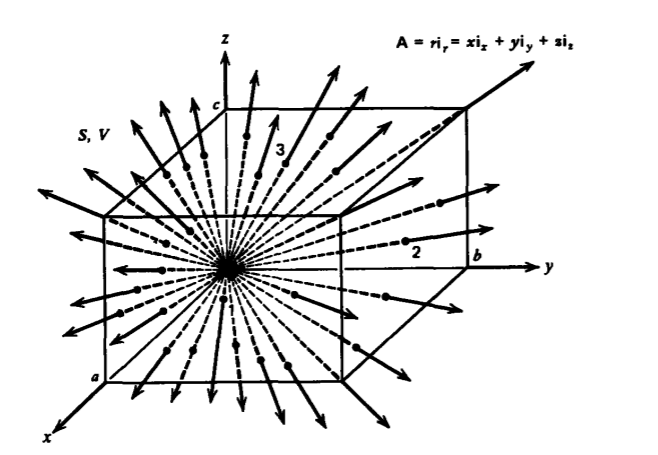
Verificar el teorema de divergencia para el vector

\(\textbf{A} = x \textbf{i}_{x} + y \textbf{i}_{y} + z \textbf{i}_{z} = r \textbf{i}_{r}\)

evaluando ambos lados de (12) para el volumen rectangular mostrado en la Figura 1-18.

Solución

La integral de volumen es más fácil de evaluar ya que la divergencia de A es una constante

\(\nabla \cdot \textbf{a} = \frac{\partial A_{x}}{\partial x} + \frac{\partial A_{y}}{\partial y} + \frac{\partial A_{z}}{\partial z} = 3\)

Figura 1-18 El teorema de divergencia se verifica en el Ejemplo 1-6 para el vector radial a través de un volumen rectangular.

(En coordenadas esféricas\(\nabla \cdot \textbf{A} = (1/r^{2})(\partial/\partial r)(r^{3}) = 3\) para que el volumen integral en (12) sea

\(\int_{V} \nabla \cdot \textbf{A} dV = 3abc\)

El flujo pasa a través de las seis superficies planas mostradas:

\(\Phi = \oint_{S} \textbf{A} \cdot \textbf{dS} = \int_{1} \underbrace{A_{x}(a)}_{a} dy dz - \int_{1'} \underbrace{A_{x}(0))}_{0} \nearrow ^{0} dy dz \\ + \int_{2} \underbrace{A_{y}(b)}_{b} dx dz - \int_{2'} \underbrace{A_{y}(0)}_{0} \nearrow ^{0} dx dz \\ + \int_{3} \underbrace{A_{z}(c)}_{c} dx dy - \int_{3'} \underbrace{A_{z}(0)}_{0} \nearrow^{0} dx dy = 3abc\)

que verifica el teorema de la divergencia.