4.4: Soluciones de Producto en Geometría Esférica

En coordenadas esféricas, la ecuación de Laplace es

\[\frac{1}{r^{2}} \frac{\partial}{\partial r} \bigg( r^{2} \frac{\partial V}{\partial r} \bigg) + \frac{1}{r^{2} \sin^{2} \theta} \frac{\partial^{2}V}{\partial \phi^{2}} = 0 \nonumber \]

4-4-1 Soluciones unidimensionales

Si la solución solo depende de una sola coordenada espacial, las ecuaciones gobernantes y las soluciones para cada una de las tres coordenadas son

(i)

\[\frac{d}{dr} \bigg( r^{2} \frac{dV(r)}{dr} \bigg) = 0 \Rightarrow V(r) = \frac{A_{1}}{r} + A_{2} \nonumber \]

ii)

\[ \frac{d}{d \theta} \bigg( \sin \theta \frac{dV(\theta)}{d \theta} \bigg) = 0 \Rightarrow V(\theta) = B_{1} \ln \bigg( \tan \frac{\theta}{2} \bigg) + B_{2} \nonumber \]

iii)

\[\frac{d^{2} V(\phi)}{d \phi^{2}} = 0 \Rightarrow V (\phi) = C_{1} \phi + C_{2} \nonumber \]

Reconocemos la solución radialmente dependiente como el potencial debido a una carga puntual. Las nuevas soluciones son aquellas que sólo dependen de\(\theta\) o\(\phi\).

Ejemplo 4-2: Dos Conos

Dos conos idénticos con superficies en ángulos\(\theta = \alpha\)\(\theta = \pi - \alpha\) y con vértices que se encuentran en el origen, se encuentran en una diferencia de potencial v, como se muestra en la Figura 4-11. Encuentra el potencial y el campo eléctrico.

Figura 4-11 Dos conos con vértices que se encuentran en el origen están en una diferencia de potencial v.

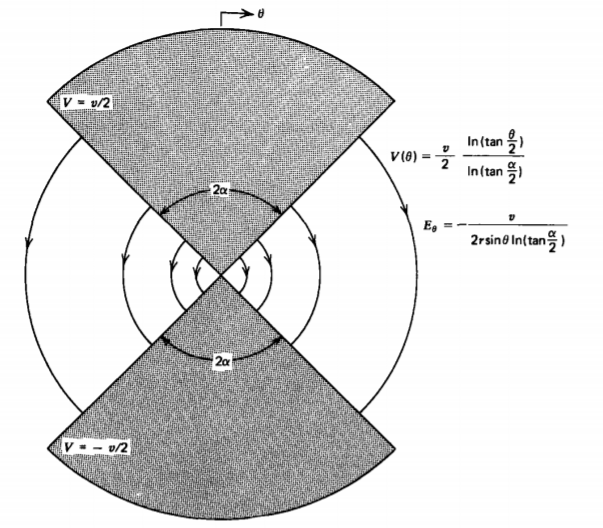
Solución

Debido a que los límites están en valores constantes de\(\theta\), intentamos (3) como solución:

\(V (\theta) = B_{1} \ln [ \tan (\theta/2)] + B_{2}\)

Desde las condiciones límite tenemos

\(V(\theta = \alpha) = \frac{v}{2} \\ V(\theta = \pi - \alpha) = \frac{-v}{2} \Rightarrow B_{1} = \frac{v}{2 \ln [ \tan(\alpha/2)]}, \: \: \: \: B_{2} = 0 \)

para que el potencial sea

\[V(\theta) = \frac{v}{2} \frac{\ln [ \tan (\theta/2)]}{\ln [ \tan (\alpha/2)]} \nonumber \]

con campo eléctrico

\[\textbf{E} = - \nabla V = \frac{-v}{2r \: \sin \theta \ln [ \tan (\alpha /2)]} \textbf{i}_{\theta} \nonumber \]

4-4-2 Soluciones axisimétricas

Si la solución no tiene dependencia de la coordenada\(\phi\), probamos una solución de producto

\[V(r, \theta) = R(r) \Theta (\theta) \nonumber \]

que cuando se sustituye en (1), después de multiplicar por\(r^{2}/R \Theta\), rinde

\[\frac{1}{R} \frac{d}{dr} \bigg( r^{2} \frac{dR}{dr} \bigg) + \frac{1}{\Theta \sin \theta} \frac{d}{d \theta} \bigg( \sin \theta \frac{d \Theta}{d \theta} \bigg) = 0 \nonumber \]

Debido a que cada término vuelve a ser solo una función de una sola variable, cada término es igual a una constante. Anticipando la forma de la solución, elegimos la constante de separación como n (n + 1) para que (6) se separe a

\[\frac{d}{dr} \bigg( r^{2} \frac{dR}{dr} \bigg) - n (n+1) R = 0 \\ \frac{d}{d \theta} \bigg( \sin \theta \frac{d \Theta}{d \theta} \bigg) + n (n + 1) \Theta \sin \theta = 0 \nonumber \]

Para la dependencia radial intentamos una solución de ley de potencia

\[R = A r^{p} \nonumber \]

que cuando se vuelve a sustituir en (7) requiere

\[p(p + 1) = n (n + 1) \nonumber \]

que cuenta con las dos soluciones

\[p = n, \: \: \: \: p = -(n+1) \nonumber \]

Cuando n = 0 volvemos a obtener la dependencia 1/ r debido a una carga puntual.

Para resolver (8) para la\(\theta\) dependencia es conveniente introducir el cambio de variable

\[\beta = \cos \theta \nonumber \]

para que

\[\frac{d \Theta}{d \theta} = \frac{d \Theta}{d \beta} \frac{d \beta}{d \theta} = - \sin \theta \frac{d \Theta}{d \beta} = - (1 - \beta^{2})^{1/2} \frac{d \Theta}{d \beta} \nonumber \]

Entonces (8) se convierte

\[\frac{d}{d \beta} \bigg( (1-\beta^{2}) \frac{d \Theta}{d \beta} \bigg) + n (n + 1) \Theta = 0 \nonumber \]

que se conoce como la ecuación de Legendre. Cuando n es un entero, las soluciones se escriben en términos de nuevas funciones:

\[\Theta = B_{n} P_{n} (\beta) + C_{n} Q_{n} (\beta) \nonumber \]

donde\(P_{n} (\beta)\) se denominan polinomios Legendre de primer tipo y se tabulan en la Tabla 4-1. Las soluciones Q _n se denominan funciones Legendre del segundo tipo para las cuales las primeras también se tabulan en la Tabla 4-1. Dado que todos los Q _n son singulares at\(\theta = 0\) y\(\theta = \pi\)\(\beta = \pm 1\), donde, para todos los problemas que incluyen estos valores de ángulo, los coeficientes _Cn en (15) deben ser cero, por lo que muchos problemas solo involucran a los polinomios Legendre de primer tipo, \(P_{n}( \cos \theta)\). Luego usando (9) - (11) y (15) en (5), la solución general para el potencial sin\(\phi\) dependencia puede escribirse como

\[V(r, \theta) = \sum_{n=0}^{\infty} (A_{n}r^{n} + B_{n}r^{-(n+1)}) P_{n}(\cos \theta) \nonumber \]

Cuadro 4-1 Polinomios Legendre de primer y segundo tipo

n	\( P_{n}(\beta = \cos \theta)\)	\(Q_{n}(\beta = \cos \theta)\)
0	1	\(\frac{1}{2} \ln \bigg( \frac{1 + \beta}{1 - \beta} \bigg)\)
1	\(\beta = \cos \theta\)	\(\frac{1}{2} \beta \ln \bigg( \frac{1 + \beta}{1 - \beta} \bigg) - 1\)
2	\(\frac{1}{2}(3 \beta^{2} - 1) = \frac{1}{2} (3 \cos^{2} \theta =1)\)	\(\frac{1}{4}(3 \beta^{2}-1) \ln \bigg( \frac{1 + \beta}{1 - \beta}\bigg) - \frac{3 \beta}{2}\)
3	\(\frac{1}{2}(5 \beta^{3} - 3 \beta) = \frac{1}{2}(5 \cos^{3} \theta - 3 \cos \theta)\)	\(\frac{1}{4}(5 \beta^{3} - 3 \beta) \ln \bigg( \frac{1 + \beta}{1 - \beta} \bigg) - \frac{5}{2} \beta^{2} + \frac{2}{3}\)
...
m	\(\frac{1}{2^{m}m!} \frac{d^{m}}{d \beta^{m}}(\beta^{2} - 1)^{m}\)

4-4-3 Esfera conductora en un campo uniforme

(a) Solución de campo

Una esfera de radio R, permitividad\(\varepsilon_{2}\) y conductividad óhmica\(\sigma_{2}\) se coloca dentro de un medio de permitividad\(\varepsilon_{1}\) y conductividad\(\sigma_{1}\). Se aplica un campo eléctrico\(E_{0} \textbf{i}_{x}\) de CC uniforme al infinito. Si bien la solución general de (16) requiere un número infinito de términos, la forma del campo uniforme al infinito en coordenadas esféricas,

\[\textbf{E}(r \rightarrow \infty) = E_{0} \textbf{i}_{z} = E_{0}(\textbf{i}_{r} \cos \theta - \textbf{i}_{\theta} \sin \theta ) \nonumber \]

sugiere que todas las condiciones de contorno se pueden cumplir con solo la solución n = 1:

\[V(r, \theta) = \left \{ \begin{matrix} Ar \: \cos \theta, & r \leq R \\ (Br + C/r^{2}) \cos \theta, & r \geq R \end{matrix} \right. \nonumber \]

No incluimos la\(1/r^{2}\) solución dentro de la esfera (r < R) ya que el potencial debe permanecer finito a r =0. El campo eléctrico asociado es

\[\textbf{E} = - \nabla V = \left \{ \begin{matrix} - A (\textbf{i}_{r} \cos \theta - \textbf{i}_{\theta} \sin \theta) = -A \textbf{i}_{z}, & r<R \\ -(B- 2 C/r^{3}) \cos \theta \textbf{i}_{r} + (B + C/r^{3}) \sin \theta \textbf{i}_{\theta}, & r > R \end{matrix} \right. \nonumber \]

El campo eléctrico dentro de la esfera es uniforme y z dirigido mientras que la solución exterior está compuesta por el campo dirigido z uniforme, pues como\(r \rightarrow \infty\) el campo debe acercarse (17) de manera que\(B = -E_{0}\), más el campo debido a un dipolo puntual en el origen, con momento dipolo

\[p_{z} = 4 \pi \varepsilon_{1}C \nonumber \]

Las condiciones adicionales de límite en estado estacionario son la continuidad del potencial a r = R [equivalente a la continuidad de E tangencial (r = R)], y la continuidad de la corriente normal a r = R,

\[V(r=R_{+}) = V(r = R_{-}) \Rightarrow E_{\theta} (r = R_{+}) = E_{\theta}(r = R_{-}) \\ \Rightarrow AR = BR + CR^{2} \\ J_{r} (r = R_{+}) = J_{r}(r = R_{-}) \Rightarrow \sigma_{1} E_{r} (r = R_{+}) = \sigma_{2} E_{r} (r = R_{-}) \\ \Rightarrow \sigma_{1}(B - 2 C/R^{3}) = \sigma_{2}A \nonumber \]

para lo cual las soluciones son

\[A = - \frac{3 \sigma_{1}}{2 \sigma_{1} + \sigma_{2}} E_{0}, \: \: \: \: B = - E_{0}, \: \: \: \: C = \frac{(\sigma_{2} - \sigma_{1})R^{3}}{2 \sigma_{1} + \sigma_{2}} E_{0} \nonumber \]

El campo eléctrico de (19) es entonces

\[\textbf{E} = \left \{ \begin{matrix} \frac{3 \sigma_{1} E_{0}}{2 \sigma_{1} + \sigma_{2}} (\textbf{i}_{r} \cos \theta - \textbf{i}_{\theta} \sin \theta) = \frac{3 \sigma_{1} E_{0}}{2 \sigma_{1} + \sigma_{2}} \textbf{i}_{z}, & r <R \\ E_{0} \bigg[ \bigg( 1 + \frac{2 R^{3} (\sigma_{2} - \sigma_{1})}{r^{3} (2 \sigma_{1} + \sigma_{2})} \bigg) \cos \theta \textbf{i}_{r} \\ - \bigg( 1 - \frac{R^{3} (\sigma_{2} - \sigma_{1})}{r^{3}(2 \sigma_{1} + \sigma_{2})} \bigg) \sin \theta \textbf{i}_{\theta} \bigg], & r > R \end{matrix} \right. \nonumber \]

La carga superficial interfacial es

\[\sigma_{f} (r = R) = \varepsilon_{1} E_{r} (r = R_{+}) - \varepsilon_{2} E_{r} (r = R_{-}) \\ = \frac{3 (\sigma_{2} \varepsilon_{1} - \sigma_{1} \varepsilon_{2}) E_{0}}{2 \sigma_{1} + \sigma_{2}} \cos \theta \nonumber \]

que es de un signo en la parte superior de la esfera y de signo opuesto en la mitad inferior de la esfera. La carga total en toda la esfera es cero. La carga es cero en cada punto de la esfera si los tiempos de relajación en cada región son iguales:

\[\frac{\varepsilon_{1}}{\sigma_{1}} = \frac{\varepsilon_{2}}{\sigma_{2}} \nonumber \]

La solución si ambas regiones fueran dieléctricos sin pérdidas sin carga superficial interfacial, es similar en forma a (23) si reemplazamos las conductividades por sus respectivas permitividades.

(b) Trazado de líneas de campo

Como vimos en la Sección 4-3-2b para una geometría cilíndrica, el campo eléctrico en una región libre de carga volumétrica no tiene divergencia, por lo que se puede expresar como el rizo de un vector. Para un campo axisimétrico en coordenadas esféricas escribimos el campo eléctrico como

\[\textbf{E}(r, \theta) = \nabla \times \bigg( \frac{\Sigma (r, \theta)}{r \sin \theta} \textbf{i}_{\phi} \bigg) \\ = \frac{1}{r^{2} \sin \theta} \frac{\partial \Sigma}{\partial \theta} \textbf{i}_{r} - \frac{1}{r \sin \theta} \frac{\partial \Sigma}{\partial r} \textbf{i}_{\theta} \nonumber \]

Obsérvese nuevamente, que para un campo eléctrico bidimensional, el vector de función de flujo apunta en la dirección ortogonal a ambos componentes de campo para que su rizo tenga componentes en la misma dirección que el campo. La función stream\(\Sigma\) se divide por\(r \sin \theta\) para que las derivadas parciales en (26) solo operen\(\Sigma\).

Las líneas de campo son tangentes al campo eléctrico

\[\frac{dr}{r d \theta} = \frac{E_{r}}{E_{\theta}} = - \frac{1}{r} \frac{\partial \Sigma/ \partial \theta}{\partial \Sigma/ \partial r} \nonumber \]

que después de la multiplicación cruzada rinde

\[d \Sigma = \frac{\partial \Sigma}{\partial r} + \frac{\partial \Sigma}{\partial \theta} = 0 \Rightarrow \Sigma = \textrm{const} \nonumber \]

para que de nuevo\(\Sigma\) sea constante a lo largo de una línea de campo.

Para la solución de (23) fuera de la esfera, relacionamos los componentes del campo con la función stream usando (26) como

\[E_{r} = \frac{1}{r^{2} \sin \theta} \frac{\partial \Sigma}{\partial \theta} = E_{0} \bigg(1 + \frac{2R^{3}(\sigma_{2} - \sigma_{1})}{r^{3}(2 \sigma_{1} + \sigma_{2})} \bigg) \cos \theta \\ E_{\theta} = - \frac{1}{r \sin \theta} \frac{\partial \Sigma}{\partial r} = - E_{0} \bigg( 1 - \frac{R^{3}(\sigma_{2} - \sigma_{1})}{r^{3}(2 \sigma_{1} + \sigma_{2})} \bigg) \sin \theta \nonumber \]

de modo que mediante la integración la función stream es

\[\Sigma = E_{0} \bigg( \frac{r^{2}}{2} + \frac{R^{3} (\sigma_{2} - \sigma_{1})}{r (2 \sigma_{1} + \sigma_{2})} \bigg) \sin^{2} \theta \nonumber \]

El campo de estado estacionario y las líneas equipotenciales se dibujan en la Figura 4-12 cuando la esfera está perfectamente aislante (O\(\sigma_{2} = 0\)) o perfectamente conductora (\(\sigma_{2} \rightarrow \infty\)).

Figura 4-12 Campo de estado estacionario y líneas equipotenciales alrededor de una (a) esfera perfectamente aislante o (b) perfectamente conductora en un campo eléctrico uniforme.

Figura 4-12b

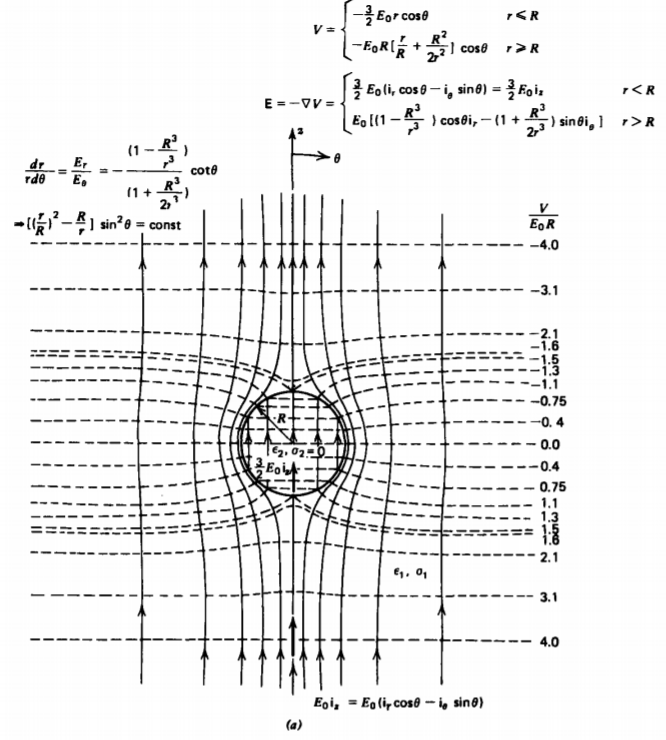
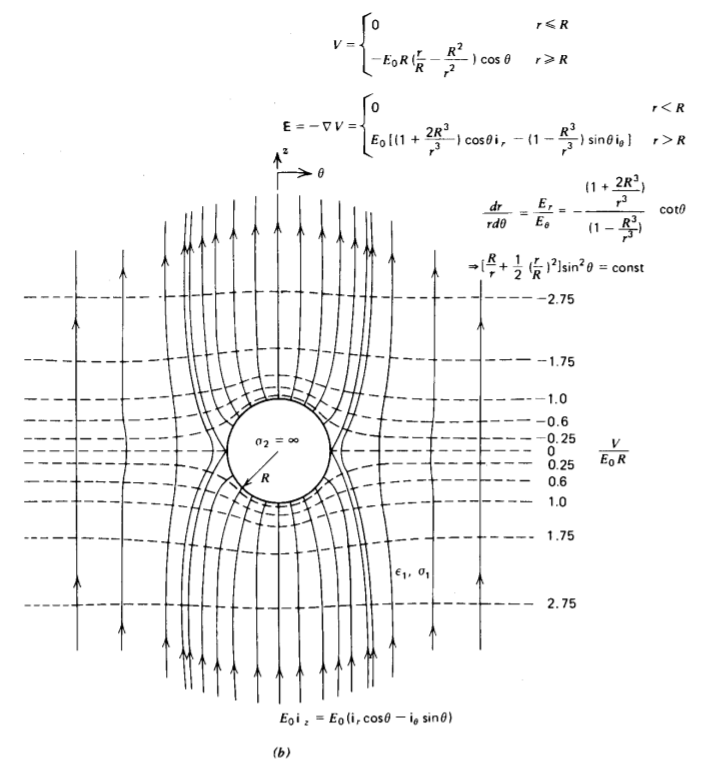
Si la conductividad de la esfera es menor que la del medio circundante (\(\sigma_{2} < \sigma_{1}\)) el campo eléctrico dentro de la esfera es mayor que el campo aplicado. Lo contrario es cierto para (\(\sigma_{2} > \sigma_{1}\)). Para la esfera aislante de la Figura 4-12a, las líneas de campo van alrededor de la esfera ya que no puede pasar ninguna corriente.

Para la esfera conductora de la Figura 4-12b, las líneas de campo eléctrico deben ser incidentes perpendicularmente. Este caso se utiliza como modelo de polarización, pues como vemos desde (23) con\(\sigma_{2} \rightarrow \infty\), el campo externo es el campo impuesto más el campo de un dipolo puntual con momento,

\[p_{z} = 4 \pi \varepsilon_{1} R^{3} E_{0} \nonumber \]

Si un dieléctrico se modela como una suspensión diluida de esferas que no interactúan perfectamente conductoras en el espacio libre con densidad numérica N, la constante dieléctrica es

\[\varepsilon = \frac{\varepsilon_{0} E_{0} + P}{E_{0}} = \frac{\varepsilon_{0} E_{0} + N p_{z}}{E_{0}} = \varepsilon_{0}(1 + 4 \pi R^{3} N) \nonumber \]

4-4-4 Precipitación de partículas cargadas sobre una esfera

La solución para una esfera perfectamente conductora rodeada de espacio libre en un campo eléctrico uniforme se ha utilizado como modelo para la carga de las gotas.* Este mismo modelo también se ha aplicado a un nuevo tipo de precipitador electrostático donde pequeñas partículas cargadas se recogen en esferas más grandes. **

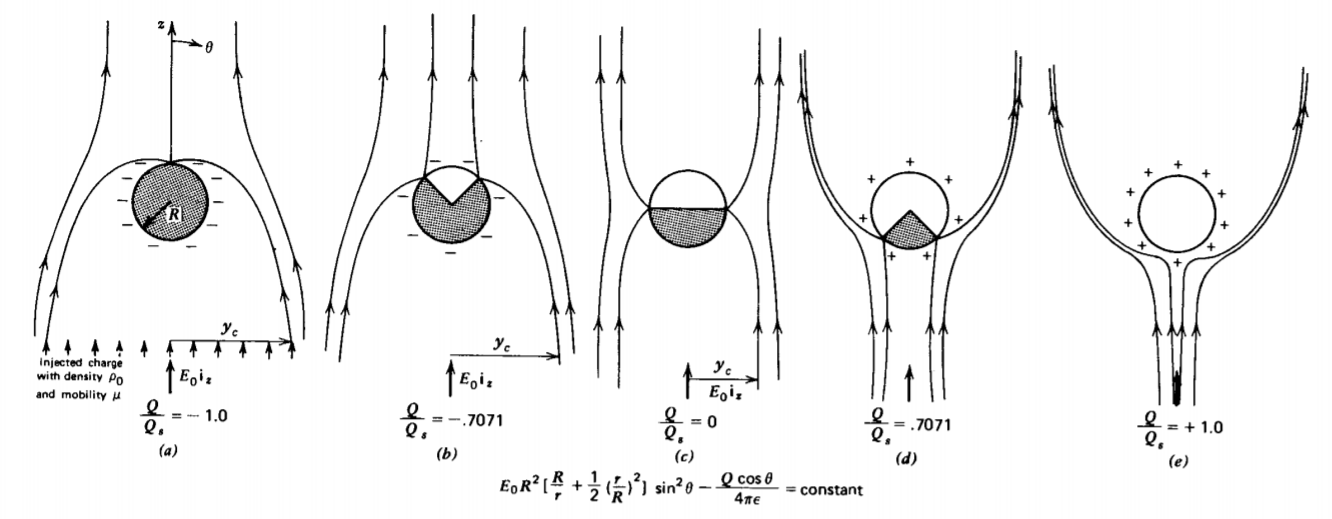
Entonces, además del campo uniforme\(E_{0}\textbf{i}_{z}\) aplicado al infinito, también se inyecta un flujo uniforme de partículas cargadas con densidad de carga\(\rho_{0}\), que tomamos para ser positivo, que viaja a lo largo de las líneas de campo con movilidad\(\mu\). Aquellas líneas de campo que inician en el infinito donde se inyecta la carga y que se acercan a la esfera con campo eléctrico radial negativo, depositan partículas cargadas, como en la Figura 4-13. La carga entonces se redistribuye uniformemente sobre la superficie equipotencial para que la carga total en la esfera aumente con el tiempo. Aquellas líneas de campo que no se cruzan con la esfera o las que arrancan en la esfera no depositan ningún cargo.

Suponemos que el autocampo debido a la carga inyectada es mucho menor que el campo aplicado\(E_{0}\). Entonces la solución de (23) con\(\sigma_{2} = \infty\) es correcta aquí, con la adición del campo radial de una esfera uniformemente cargada con carga total Q (t):

\[\textbf{E} + \bigg[ E_{0} \bigg(1 + \frac{2R^{3}}{r^{3}} \bigg) \cos \theta + \frac{Q}{4 \pi \varepsilon r^{2}} \bigg] \textbf{i}_{r} - E_{0} \bigg( 1 - \frac{R^{3}}{r^{3}} \bigg) \sin \theta \textbf{i}_{\theta}, \: \: \: \: r > R \nonumber \]

La carga solo impacta la esfera donde E _r (R=r) es negativo:

Figura 4-13 Líneas de campo eléctrico alrededor de una esfera perfectamente conductora cargada uniformemente en un campo eléctrico uniforme con inyección continua de carga positiva desde\(z = - \infty\). Solo aquellas líneas de campo que impactan en la esfera con el campo eléctrico radialmente hacia adentro [E _r (R) <0] se cargan de depósito. (a) Si la carga total sobre la esfera comienza como carga negativa con magnitud mayor o igual a la carga crítica, las líneas de campo dentro de la distancia y _c del eje z impactan sobre toda la esfera. b) - d) A medida que la esfera cobra tiende a repeler parte del cargo incidente y sólo una parte de la esfera recoge cargos. Al aumentar la carga la ventana angular para la recolección de carga disminuye al igual que y _c. (e) Pues\(Q \geq Q\), no se cobra más carga en la esfera para que la carga permanezca constante a partir de entonces. La ventana angular y y _c se han reducido a cero.

lo que nos da una ventana para la recolección de cargas en el rango de ángulo, donde

\[\cos \theta \leq - \frac{Q}{12 \pi \varepsilon E_{0} R^{2}} \nonumber \]

Dado que la magnitud del coseno debe ser menor que la unidad, la cantidad máxima de carga que se puede recolectar en la esfera es

\[Q_{s} = 12 \pi \varepsilon E_{0} R^{2} \nonumber \]

Tan pronto como se alcanza esta carga de saturación, todas las líneas de campo emanan radialmente hacia afuera de la esfera para que no se pueda recoger más carga. Definimos el ángulo crítico\(\theta_{c}\) como el ángulo donde el campo eléctrico radial es cero, definido cuando (35) es una igualdad\(\cos \theta_{c} = -Q/Q_{s}\). La densidad de corriente que carga la esfera es

\[J_{r} = \rho_{0} \mu E_{r} (r = R) \\ = 3 \rho_{0} \mu E_{0} (\cos \theta + Q/Q_{s}), \: \: \: \: \: \theta_{c} < \theta < \pi \nonumber \]

La corriente de carga total es entonces

\[\frac{dQ}{dt} = - \int_{\theta = \theta_{c}}^{\pi} J_{r} 2 \pi R^{2} \sin \theta d \theta \\ = - 6 \pi \rho_{0} \mu E_{0} R^{2} \int_{\theta = \theta_{c}}^{\pi} (\cos \theta + Q/Q_{s} \) \sin \theta d \theta \\ = -6 \pi \rho_{0} \mu E_{0} R^{2} ( - \frac{1}{4} \cos 2 \theta - (Q/Q_{s}) \cos \theta) \vert_{\theta = \theta_{c}}^{\pi} = - 6 \pi \rho_{0} \mu E_{0} R^{2} ( - \frac{1}{4} ( 1- \cos 2 \theta_{c}) + (Q/Q_{s}) ( 1 + \cos theta_{c})) \nonumber \]

Siempre y cuando\(\vert Q \vert < Q_{s}, \: \: \: \theta_{c}\) se defina por la igualdad en (35). Si Q excede Q _s, lo que solo puede ocurrir si la esfera está sobrecargada intencionalmente, entonces\(\theta_{c} = \pi\) y no puede ocurrir más carga ya que\(dQ/dt\) en (38) es cero. Si Q es negativo y excede Q _s en magnitud\(Q < -Q_{s}\), entonces toda la esfera recoge carga como\(\theta_{c} = 0\). Entonces para estas condiciones tenemos

\[\cos \theta_{c} = \left \{ \begin{matrix} -1, & Q>Q_{s} \\ -Q/Q_{s} & -Q_{s} < Q < Q_{s} \\ 1, & Q< - Q_{s} \end{matrix} \right. \nonumber \]

\[\cos 2 \theta_{c} = 2 \cos^{2} \theta_{c} - 1 = \left \{ \begin{matrix} 1, & \vert Q \vert > Q_{s} \\ 2 (Q/Q_{s})^{2} - 1, & \vert Q \vert < Q_{s} \end{matrix} \right. \nonumber \]

de manera que (38) se convierte

\[\frac{d \frac{Q}{Q_{s}}}{dt} = \left \{ \begin{matrix} 0, & Q>Q_{s} \\ \frac{\rho_{0} \mu}{4 \varepsilon} \bigg(1 - \frac{Q}{Q_{s}} \bigg)^{2}, & -Q_{s} < Q < Q_{s} \\ - \frac{\rho_{0}\mu}{\varepsilon} \frac{Q}{Q_{s}}, & Q < - Q_{s} \end{matrix} \right. \nonumber \]

con soluciones integradas

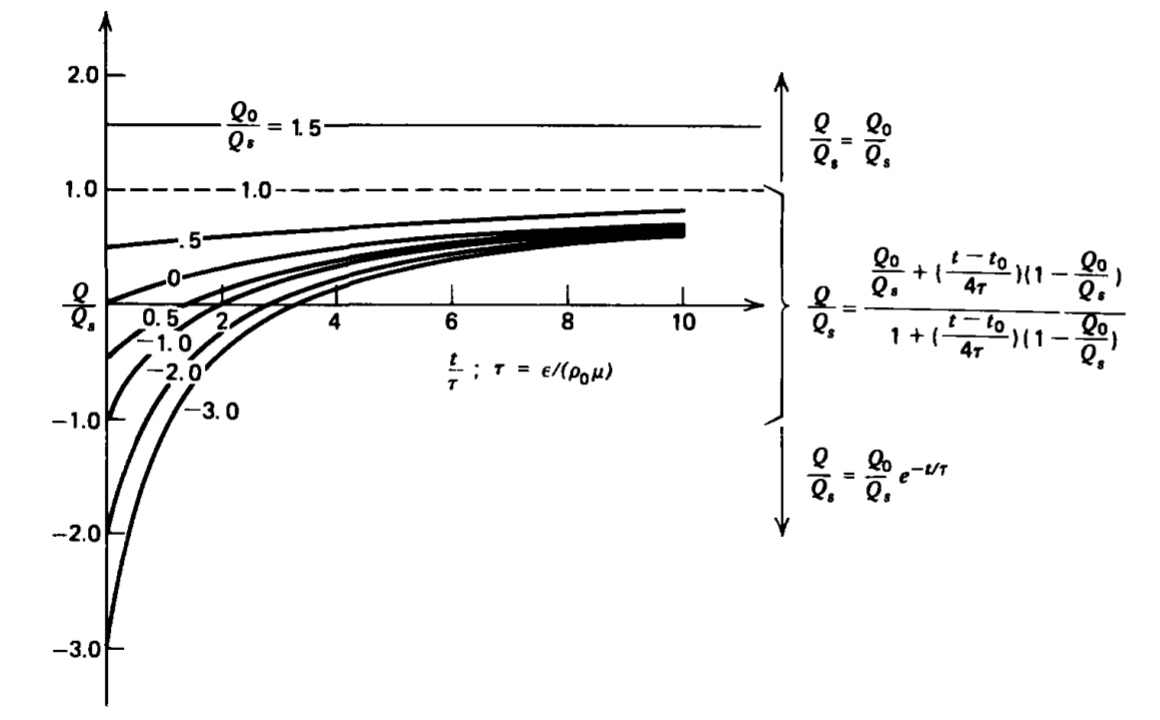
\[\frac{Q}{Q_{s}} = \left \{ \begin{matrix} \frac{Q_{0}}{Q_{s}}, & Q > Q_{s} \\ \frac{\frac{Q_{0}}{Q_{s}} + \frac{(t - t_{0})}{4 \tau} \bigg(1 - \frac{Q_{0}}{Q_{s}}\bigg)}{1 + \frac{(t-t_{0})}{4 \tau} \bigg(1 = - \frac{Q_{0}}{Q_{s}} \bigg)}, & -Q_{s} < Q < Q_{s} \\ \frac{Q_{0}}{Q_{s}} e^{-t/Tau}, & Q< -Q_{s} \end{matrix} \right. \nonumber \]

donde Q _o es la carga inicial a t =0 y el tiempo de carga característico es

\[\tau = \varepsilon/ (\rho_{0} \mu) \nonumber \]

Si la carga inicial Q ₀ es menor que - Q _s, la magnitud de la carga disminuye con la ley exponencial en (42) hasta que la carga total alcanza - Q _s a t = t ₀. Entonces la ley de carga cambia al siguiente régimen con\(Q_{0} = - Q_{s}\), donde la carga pasa por cero y se acerca lentamente asintóticamente\(Q = Q_{s}\). La carga nunca puede exceder Q _s a menos que se cargue externamente. Luego se mantiene constante a este valor repeliendo cualquier cargo adicional. Si la carga inicial Q ₀ tiene una magnitud menor que Q _s, entonces\(t_{0} = 0 \). La dependencia del tiempo de la carga se grafica en la Figura 4-14 para diversos valores de carga inicial Q ₀. No importa el valor inicial de\(Q_{0}\) for\(Q < Q_{s}\), se necesitan muchas constantes de tiempo para que la carga se acerque de cerca al valor de saturación Q _s. La fuerza de repulsión sobre la carga inyectada aumenta a medida que aumenta la carga en la esfera para que la corriente de carga disminuya.

Las líneas de campo esbozadas en la Figura 4-13 muestran cómo cambian los campos a medida que la esfera se carga. La ventana para el cobro de cargas disminuye con el aumento de la carga. Las líneas de campo se encuentran añadiendo la función stream de una esfera uniformemente cargada con carga total Q a la solución de (30)

Figura 4-14 Existen tres regímenes que describen la acumulación de carga en la esfera. Se necesitan muchas constantes de tiempo\[\tau = \varepsilon/ (\rho_{0}/mu)] \nonumber \] ['r = e/ (pos)] para que la carga se acerque al valor de saturación Q _s porque a medida que la esfera se carga la fuerza repulsiva coulómbica aumenta de manera que la mayor parte de la carga gira alrededor de la esfera. Si la esfera se carga externamente a un valor superior a la carga de saturación, permanece constante ya que toda la carga adicional se repele completamente.

con\(\sigma_{2} \rightarrow \infty\)

\[\Sigma = E_{0}R^{2} \bigg[ \frac{R}{r} + \frac{1}{2} \bigg( \frac{r}{R} \bigg) ^{2} \bigg] \sin^{2} \theta - \frac{Q \cos \theta}{4 \pi \varepsilon} \nonumber \]

La línea aerográfica que interseca la esfera en r = R,\(\theta = \theta_{c}\) separa aquellas líneas de racionalización que depositan la carga sobre la esfera de las que viajan más allá.

* Véase: F. J. W. Whipple y J. A. Chalmers, Sobre la teoría de Wilson de la colección de carga por caída de gotas, cuarto de galón. J. Roy. Met. Soc. 70, (1944), p. 103.

** Ver: H. J. White, Precipitación Electrostática Industrial Addison-Wesley, Lectura. Misa. 1963, pp. 126-137.