7.6: Incidencia normal sobre un dieléctrico

Dieléctrico sin pérdidas

Sustituimos el conductor perfecto por un dieléctrico sin pérdidas de permitividad\(\varepsilon _{2}\) y permeabilidad\(\mu _{2}\), como en la Figura 7-14, por una onda plana uniforme que normalmente incide desde un medio con permitividad\(\varepsilon _{1}\) y permeabilidad\(\mu _{1}\). Además del incidente y campos reflejados para\(z <0\), existen campos transmitidos que se propagan en la\(+z\) dirección dentro del medio para\(z >0\):

\ begin {align}\ left. \ begin {array} {ll}
\ textbf {E} _ {i}\ izquierda (z, t\ derecha) =&\ textrm {Re}\ izquierda [\ hat {E} _ {i} e^ {j\ izquierda (\ omega t-k_1 z\ derecha)}\ textbf {i} _ {x}\ derecha],\ quad k_1=\ omega\ sqrt {\ varepsilon_ {1}\ mu_ {1}}\
\ textbf {H} _ {i}\ izquierda (z, t\ derecha) =&\ textrm {Re}\ izquierda [\ frac {\ sombrero {E} _ _ {i}} {\ eta _ { 1}} e^ {j\ izquierda (\ omega t-k_1 z\ derecha)}\ textbf {i} _ {y}\ derecha],\ quad\ eta_ {1} =\ sqrt {\ frac {\ mu _ {1}} {\ varepsilon _ {1}}}\
\ textbf {E} _ _ {r}\ izquierda (z, t\ derecha) =&\ textrm {Re}\ izquierda [\ hat {E} _ {r} e^ {j\ izquierda (\ omega t+k_1 z\ derecha)}\ textbf {i} _ {x}\ derecha]\
\ textbf {H} _ {r}\ izquierda (z, t\ derecha) =&\ textrm {Re}\ izquierda [-\ frac {\ hat {E} _ {r}} {\ eta _ {1}} e^ {j\ izquierda (\ omega t+k_1 z\ derecha)}\ textbf {i} _ {y}\ derecha]
\ end {array}\ derecha\\ derecha\\ quad z<0\ nonumber\ end {align}

\ [\ begin {align}\ left. \ begin {array} {ll}
\ textbf {E} _ {t}\ izquierda (z, t\ derecha) =&\ textrm {Re}\ izquierda [\ hat {E} _ {t} e^ {j\ izquierda (\ omega t-k_2 z\ derecha)}\ textbf {i} _ {x}\ derecha],\ quad k_2=\ omega\ sqrt {varepsilon_ {2}\ mu_ {2}}\
\ textbf {H} _ {t}\ izquierda (z, t\ derecha) =&\ textrm {Re}\ izquierda [\ frac {\ sombrero {E} _ {t}} {\ eta _ {2 }} e^ {j\ izquierda (\ omega t-k_2 z\ derecha)}\ textbf {i} _ {y}\ derecha],\ quad\ eta_ {2} =\ sqrt {\ frac {\ mu _ {2}} {\ varepsilon _ {2}}}\ end {array}\ derecha\\ quad z>0\ nonumber\ end align {}\ nonumber\ nonumber\]

Es necesario en (1) usar el número de onda y la impedancia apropiados dentro de cada región. No hay onda viajando en la\(-z\) dirección en la segunda región ya que asumimos que no hay límites ni fuentes para\(z >0\).

Figura 7-14 Una onda plana uniforme que normalmente incide sobre una interfaz dieléctrica que separa dos materiales diferentes tiene parte de su potencia reflejada y parte transmitida.

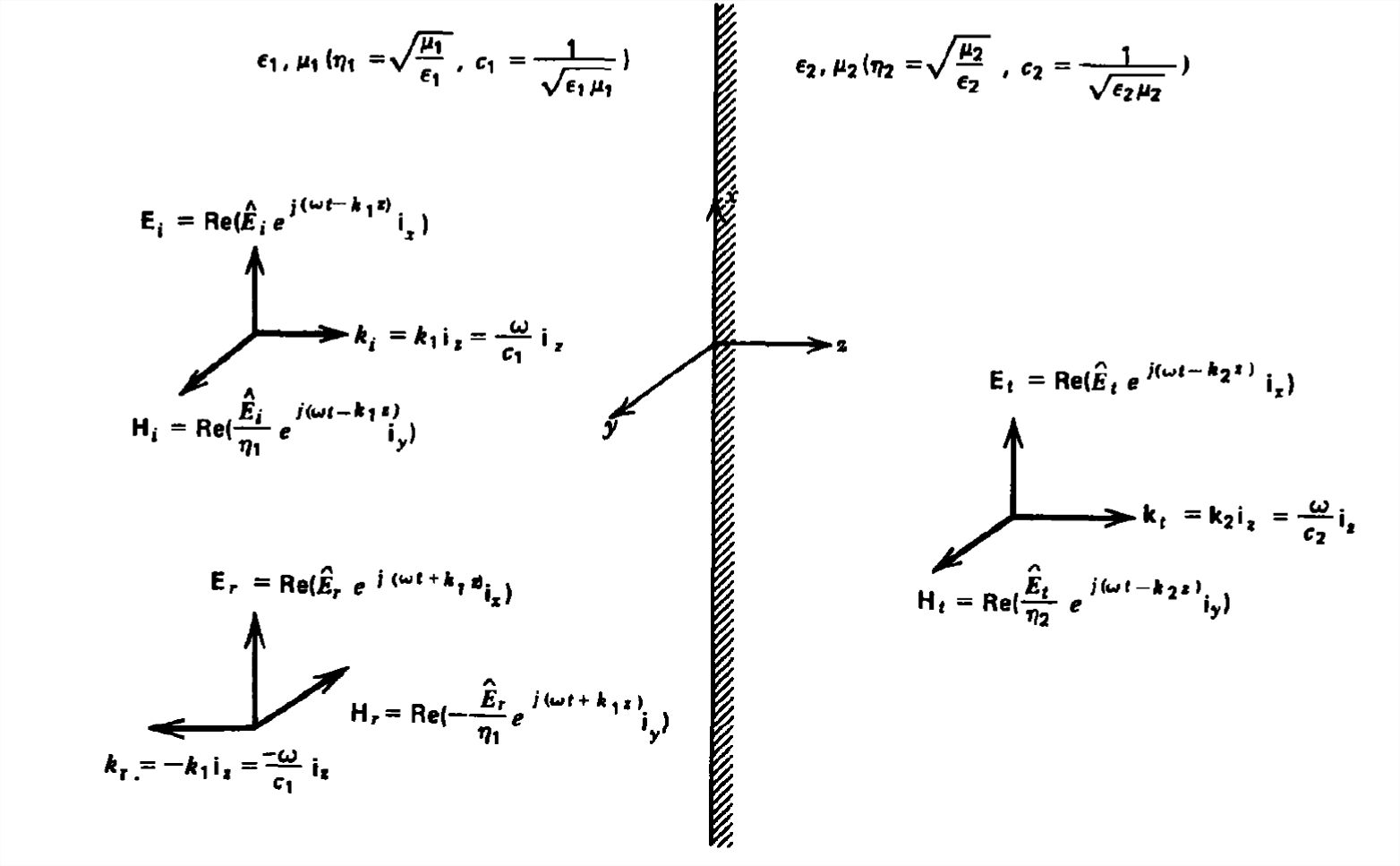
Las cantidades desconocidas\(\hat{E}_{r}\) y\(\hat{E}_{i}\), se pueden encontrar a partir de las condiciones limítrofes de continuidad de tangencial\(\textbf{E}\) y\(\textbf{H}\) a\(z = 0\),

\ [\ sombrero {E} _ {i} +\ sombrero {E} _ {r} =\ sombrero {E} _ {t}\
\ frac {\ sombrero {E} _ {i} -\ sombrero {E} _ {r}} {\ eta _ {1}} =\ frac {\ sombrero {E} _ {r}} {\ eta _ {2}}\ nonumber\]

de donde encontramos los coeficientes de\(T\) campo de reflexión\(R\) y transmisión como

\ [R=\ frac {\ sombrero {E} _ {r}} {\ sombrero {E} _ {i}} =\ frac {\ eta_ {2} -\ eta_ {1}} {\ eta_ {2} +\ eta_ {1}}\\
T=\ frac {\ sombrero {E} _ {t}} {\ sombrero {E} _ {i}} =\ frac {2\ eta_ {2}} {\ eta_ {2} +\ eta_ {1}}\ nonumber\]

donde de (2)

\[ 1+R=T \nonumber \]

Si ambos medios tienen la misma impedancia de onda\(\eta_{1}=\eta_{2}\),, no hay onda reflejada.

Flujo de potencia promedio en el tiempo

El flujo de potencia promedio en el tiempo en la región\(z <0\) es\(\)

\ [\ begin {align &= <S_ {xi} >\ frac {1} {2}\ textrm {Re}\ izquierda [\ hat {E} _ {x}\ izquierda (z\ derecha)\ hat {H} _ {y} ^ {\ ast}\ izquierda (z\ derecha)\ derecha]\ nonumber\\ &=\ frac {1} {2\ eta _ {1}}\ textrr m {Re}\ left [\ hat {E} _ {i} e^ {-jk_ {1} z} +\ hat {E} _ {r} e^ {+jk_ {1} z}\ derecha]\ izquierda [\ hat {E} _ {i} ^ {\ ast} e^ {+jk_ {1} z} +\ hat {E} _ {r} ^ ^\ ast} e^ {-jk_ {1} z}\ derecha]\ nonumber\\ &=
\ frac {1} {2\ eta _ {1}}\ izquierda [\ izquierda |\ sombrero {E} _ {i}\ derecha |^ {2} -\ izquierda |\ sombrero {E} _ {r}\ derecha |^ {2}\ derecha]\ nonumber\\ {} y\ +\ frac {1} {2\ eta _ {1}}\ underbrackets {\ textrm {Re}\ izquierda [\ hat {E} _ {r}\ hat {E} _ {i} ^ {\ ast} e^ {+2jk_ {1} z} -\ hat {E} _ _ {r} ^ {\ ast}\ hat {E} _ {i} e^ {- 2jk_ {1} z}\ derecha]} _0\ end {align}\ nonumber\]

El último término en el lado derecho de (5) es cero ya que es la diferencia entre un número y su complejo conjugado, que es puro imaginario e igual a\(2j\) veces su parte imaginaria. Siendo puro imaginario, su parte real es cero. Así, el flujo de potencia promedio en el tiempo solo equivale a la diferencia en los flujos de potencia en las ondas incidentes y reflejadas como se encuentra más generalmente en la Sección 7-3-2. Los términos de acoplamiento entre ondas que viajan opuestamente no tienen promedio de tiempo, lo que produce la superposición simple de potencias promedio en el tiempo:

\[ \begin{align} <S_{xi}>&=\frac{1}{2\eta _{1}}\left [ \left | \hat{E}_{i} \right |^{2} -\left | \hat{E}_{r} \right |^{2}\right ]\nonumber \\ &=\frac{\left | \hat{E}_{i} \right |^{2}}{2\eta _{1}}\left [ 1-R^{2} \right ]\end{align} \nonumber \]

Esta potencia media neta en el tiempo fluye hacia el medio dieléctrico, ya que también es igual a la potencia transmitida;

\ ]= <S_ {xi} >\ frac {1} {2\ eta _ {2}}\ izquierda |\ sombrero {E} _ {t}\ derecha |^ {2} =
\ frac {\ izquierda |\ sombrero {E} _ _ {i}\ derecha |^ {2} T^ {2}} {2\ eta _ {2}} =
\ frac {\ izquierda |\ sombrero {E} _ {i}\ derecha |^ {2}} {2\ eta _ {1}}\ izquierda [1-R^ {2}\ derecha]\ nonumber\]

Dieléctrico con pérdida

Si el medio\(2\) tiene pérdidas con conductividad óhmica\(\sigma \), las soluciones de (3) siguen siendo correctas si reemplazamos la permitividad\(\varepsilon_{2}\) por la permitividad compleja\(\hat{\varepsilon}_{2}\),

\[ \hat{\varepsilon}_{2}= \varepsilon_{2}\left ( 1+\frac{\sigma }{j\omega \varepsilon_{2}} \right ) \nonumber \]

para que la impedancia de onda en la región\(2\) sea compleja:

\[ \eta _{2}= \sqrt{\mu _{2}/\hat{\varepsilon}_{2}} \nonumber \]

Podemos explorar fácilmente el efecto de las pérdidas en los límites de pérdidas bajas y grandes.

(a) Pérdidas bajas

Si la conductividad óhmica es pequeña, podemos descuidarla en todos los términos excepto en el número de onda\(k_2\):

\[ \lim_{\sigma /\omega \varepsilon _{2}\ll 1}k_{2}\approx \omega \sqrt{\varepsilon _{2}\mu _{2}}-\frac{j}{2}\sigma \sqrt{\frac{\mu _{2}}{\varepsilon _{2}}} \nonumber \]

La parte imaginaria\(k_2\) da lugar a una pequeña tasa de decaimiento exponencial en medio a\(2\) medida que la onda se propaga lejos del\(z =0\) límite.

b) Grandes pérdidas

Para grandes conductividades para que la corriente de desplazamiento sea insignificante en medio\(2\), el número de onda y la impedancia en la región\(2\) son complejos:

\ [\ lim_ {\ sigma/\ omega\ varepsilon _ {2}\ gg 1}\ izquierda\ {\ comenzar {matriz}
k_ {2} =\ frac {1-j} {\ delta},\ quad\ delta =\ sqrt {\ frac {2} {\ omega\ mu _ {2}\ sigma}}\
\ eta _ {2} =\ sqrt {frac {j\ omega\ mu _ {2}} {\ sigma}} =\ frac {1+j} {\ sigma\ delta}
\ end {matrix}\ right.
\ nonumber\]

Los campos se descomponen dentro de una distancia característica igual a la profundidad de la piel\(\delta \). Es por ello que las comunicaciones a los submarinos sumergidos son difíciles. Para el agua de mar,\(\mu _{2}=\mu _{0}=4\pi \times 10^{-7} \,\textrm{henry/m}\) y para\(\sigma \approx 4 \,\textrm{siemens/m}\) que para\(1 \,\textrm{MHz}\) las señales,\(\delta \approx 0.25 \,\textrm{m}\). Sin embargo, a\(100\,\textrm{Hz}\) la profundidad de la piel aumenta a\(25\,\textrm{meters}\). Si un submarino se encuentra a esta distancia de la superficie, puede recibir las señales. Sin embargo, es difícil transmitir estas bajas frecuencias debido a la gran longitud de onda del espacio libre,\(\lambda \approx 3\times 10^{6}\,\textrm{m}\). Tenga en cuenta que a medida que la conductividad se acerca al infinito

\ [\ lim_ {\ sigma\ fila derecha\ infty}\ izquierda\ {\ comenzar {matriz}
k_ {2} =\ infty\\
\ eta _ {2} =0
\ end {matriz}\ derecha. \ Rightarrow\ left\ {\ begin {matrix}
R=-1\\
T=0
\ end {matrix}\ right. \ nonumber\]

de manera que la solución de campo se aproxime a la de incidencia normal sobre un conductor perfecto que se encuentra en la Sección 7-5.

Ejemplo\(\PageIndex{1}\) EXAMPLE 7-1 DIELECTRIC COATING

Un dieléctrico delgado sin pérdidas con permitividad\(\varepsilon \) y permeabilidad\(\mu \) se recubre sobre la interfaz entre dos medios infinitos de medios sin pérdidas con propiedades respectivas\(\left ( \varepsilon_{1},\mu_{1} \right )\) y\(\left ( \varepsilon _{2},\mu _{2} \right )\), como se muestra en la Figura 7-15. Qué parámetros de recubrimiento\(\varepsilon \) y\(\mu \) M y espesor\(d\) permitirán toda la potencia promedio de tiempo

Figura 7-15 Un recubrimiento dieléctrico adecuado aplicado sobre la interfaz de discontinuidad entre diferentes medios puede eliminar reflexiones a una frecuencia dada.

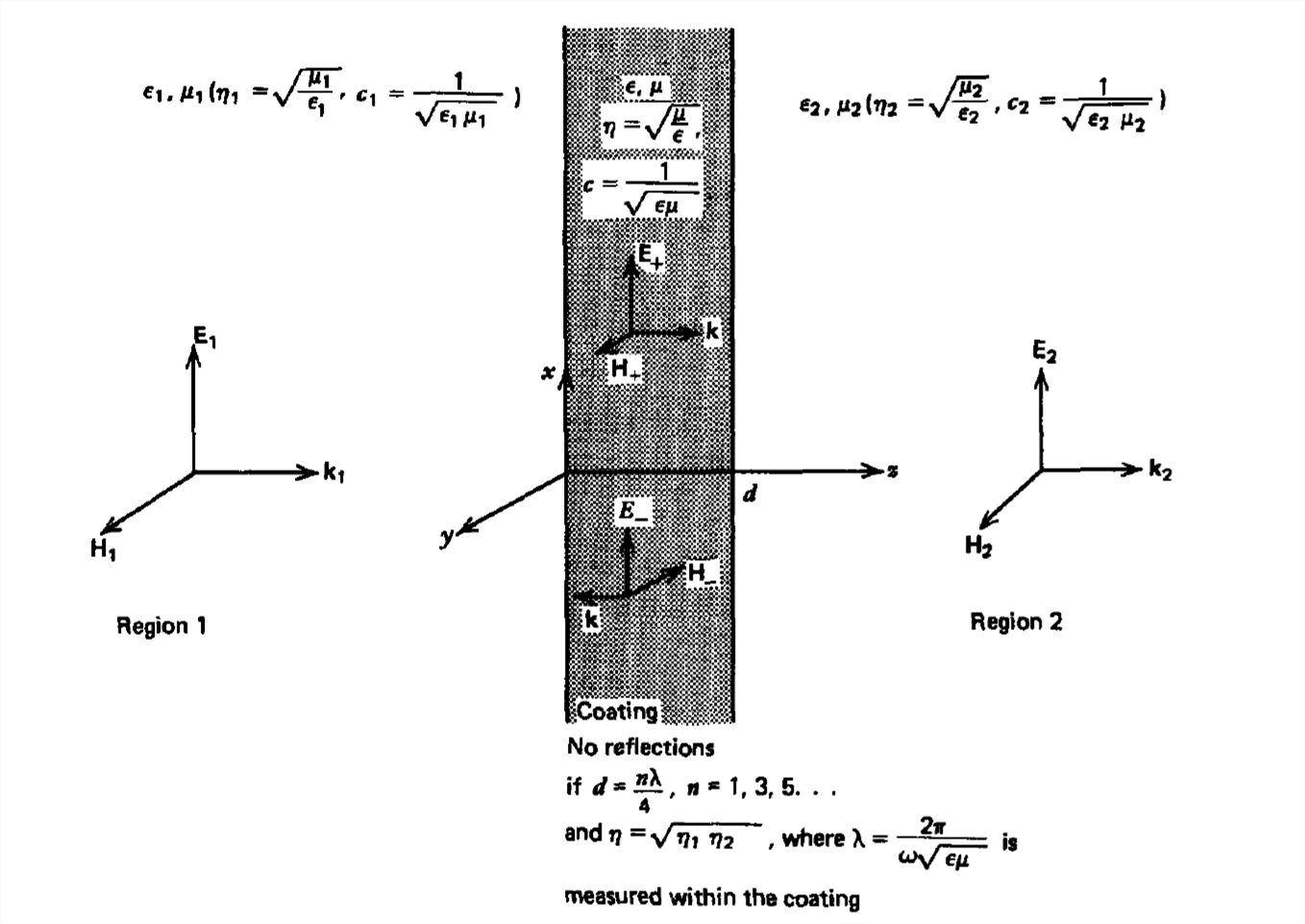
de región\(1\) a transmitir a través del recubrimiento a región\(2\)? Dichos recubrimientos se aplican a componentes ópticos tales como lentes para minimizar las reflexiones no deseadas y maximizar la intensidad de la luz transmitida.

SOLUCIÓN

Para que toda la potencia incidente se transmita a la región\(2\), no puede haber campo reflejado en la región\(1\), aunque sí tenemos ondas que viajan de manera opuesta en el recubrimiento debido a la reflexión en la segunda interfaz. La región\(2\) solo tiene flujo\(z\) de potencia dirigido positivamente. Los campos en cada región son así de la siguiente forma:

Región 1

\ [\ textbf {E} _ _ {1} =\ textrm {Re}\ izquierda [\ hat {E} _ {1} e^ {j\ izquierda (\ omega t-k_1 z\ derecha)}\ textbf {i} _ {x}\ derecha],\ quad k_1=\ omega /c_ {1} =\ omega\ sqrt {\ varepsilon _ {1}\ mu _ {1}}\
\ textbf {H} _ {1} =\ textrm {Re}\ left [\ frac {\ hat {E} _ {1}} {\ eta _ {1}} e^ {j\ izquierda (\ omega t-k_1 z\ derecha)}\ textbf {i} _ {y}\ derecha],\ quad\ eta_1=\ sqrt {\ frac {\ mu _ {1}} {\ varepsilon _ {1}}}\ nonumber\]

Recubrimiento

\ [\ begin {align}\ textbf {E} _ {+} & =\ textrm {Re}\ izquierda [\ hat {E} _ {+} e^ {j\ izquierda (\ omega t-kz\ derecha)}\ textbf {i} _ {x}\ derecha],\ quad k=\ omega /c =\ omega\ sqrt {\ varepsilon\ mu} nonumber\\
\ textbf {H} _ {+} & =\ textrm {Re}\ izquierda [\ frac {\ sombrero {E} _ {+}} {\ eta} e^ {j\ izquierda (\ omega t-kz\ derecha)}\ textbf {i} _ _ {y}\ derecha],\ quad\ eta_1=\ sqrt {\ frac {\ mu} {\ varepsilon}}\ nonumber\
\ textbf {E} _ {-} & =\ textrm {Re}\ izquierda [\ hat {E} _ {-} e^ {j\ izquierda (\ omega t+kz\ derecha)}\ textbf {i} _ {x}\ derecha]\ nonumber\\
\ textbf {H} _ {-} & =\ textrm {Re}\ izquierda [-\ frac {\ hat {E} _ {-} _ {-}} {\ eta} e^ {j\ izquierda (\ omega t+kz\ derecha)}\ textbf {i} _ {y}\ derecha]\ end {align}\ nonumber\]

Región 2

\ [\ textbf {E} _ _ {2} =\ textrm {Re}\ izquierda [\ hat {E} _ {2} e^ {j\ izquierda (\ omega t-k_2 z\ derecha)}\ textbf {i} _ {x}\ derecha],\ quad k_2=\ omega /c_ {2} =\ omega\ sqrt {\ varepsilon _ {2}\ mu _ {2}}\
\ textbf {H} _ _ {2} =\ textrm {Re}\ left [\ frac {\ hat {E} _ {2}} {\ eta _ {2}} e^ {j\ izquierda (\ omega t-k_2 z\ derecha)}\ textbf {i} _ {y}\ derecha],\ quad\ eta_2=\ sqrt {\ frac {\ mu _ {2}} {\ varepsilon _ {2}}}\ nonumber\]

Continuidad de tangencial\(\textbf{E}\) y\(\textbf{H}\) en\(z =0\) y\(z =d\) requiere

\ [\ sombrero {E} _ {1} =\ sombrero {E} _ {+} +\ sombrero {E} _ {-},\ quad\ frac {\ sombrero {E} _ {1}} {\ eta _ {1}} =\ frac {\ sombrero {E} _ {+} -\ sombrero {E} _ {-} _ {-} {\ eta}
\\ sombrero {E} _ {+} e^ {-jkd} +\ sombrero {E} _ {-} e^ {+jkd} =\ sombrero {E} _ {2} e^ {-jk_ {2} d}\\
\ frac {\ sombrero {E} _ _ {+} e^ {-jkd} -\ sombrero {E} _ _ {-} e^ {+jkd}} {\ eta} = frac {\ hat {E} _ {2} e^ {-jk_ {2} d}} {\ eta _ {2}}\ nonumber\]

Cada una de estas amplitudes en términos de\(\hat{E}_{1}\) es entonces

\ [\ begin {align}\ hat {E} _ {+} & =\ frac {1} {2}\ izquierda (1+\ frac {\ eta} {\ eta} {\ eta _ {1}}\ sombrero {E} _ {1}\ derecha)\ nonumber
\\ sombrero {E} _ _ {-} & =\ frac {1} {2}\ izquierda (1-\ frac {eta} {\ eta _ {1}}\ sombrero {E} _ {1}\ derecha)\ nonumber\
\ sombrero {E} _ {2} &=e^ {jk_ {2} d}\ izquierda [\ sombrero {E} _ {+} e^ {-jkd} +\ hat {E} _ _ {-} e^ {+jkd}\ derecha]\ nonumber\\ &=\ frac {\ eta _ {2}} {\ eta} e^ {jk_ {2} d}\ izquierda [\ hat {E} _ {+} e^ {-jkd} -\ hat {E} _ {-} e^ {+jkd}\ derecha]\ end {align}\ nonumber\]

Resolver esta última relación de manera autoconsistente requirió que

\[ \hat{E}_{+}e^{-jkd}\left ( 1-\frac{\eta _{2}}{\eta}\right )+ \hat{E}_{-}e^{jkd}\left ( 1+\frac{\eta _{2}}{\eta}\right )=0 \nonumber \]

Redacción\(\hat{E}_{+}\) y\(\hat{E}_{-}\) en términos de\(\hat{E}_{1}\) rendimientos

\[ \left ( 1+\frac{\eta}{\eta_{1}}\right )\left ( 1-\frac{\eta _{2}}{\eta}\right )+e^{2jkd}\left ( 1+\frac{\eta _{2}}{\eta}\right )\left ( 1-\frac{\eta}{\eta_{1}}\right )=0 \nonumber \]

Dado que esta relación es compleja, las partes real e imaginaria deben satisfacerse por separado. Para que la parte imaginaria sea cero requiere que el espesor del recubrimiento\(d\) sea un número integral de cuartos de longitud de onda medidos dentro del recubrimiento,

\[ 2kd=n\pi \Rightarrow d=n\lambda /4,\quad n=1,2,3 \nonumber \]

La parte real requiere entonces

\ [\ izquierda (1+\ frac {\ eta} {\ eta_ {1}}\ derecha)\ izquierda (1-\ frac {\ eta _ {2}} {\ eta}\ derecha)\ pm\ izquierda (1+\ frac {\ eta _ {2}} {\ eta}\ derecha)\ izquierda (1-\ frac {\ eta} {\ eta} {\ eta}\ derecha) =0\ izquierda\ {\ comenzar {matriz}
n\,\ textrm {par}\\ n\,\ textrm {impar}\ final {matriz}\ derecha. \ nonumber\]

Para el signo superior donde\(d\) hay un múltiplo de medias longitudes de onda, la única solución es

\[ \eta_{2}=\eta_{1}\quad \left ( d=n\lambda /4,\quad n=2,4,6,... \right ) \nonumber \]

lo que requiere ese medio\(1\) y\(2\) ser el mismo para que el recubrimiento no sirva para ningún propósito. Si las regiones\(1\) y\(2\) tienen impedancias de onda diferentes, debemos usar el signo inferior donde\(d\) es un número entero impar de longitudes de onda de un cuarto de manera que

\[ \eta ^{2}=\eta_{1}\eta_{2}\Rightarrow \eta = \sqrt{\eta_{1}\eta_{2}}\quad \left ( d=n\lambda /4,\quad n=1,3,5,... \right ) \nonumber \]

Por lo tanto, si el recubrimiento tiene un espesor de un cuarto de longitud de onda medido dentro del recubrimiento, o cualquier múltiplo entero impar de este espesor con su impedancia de onda igual al promedio geométrico de las impedancias en cada región adyacente, todo el flujo de potencia promedio en el tiempo en la región\(1\) pasa a través del recubrimiento hacia región\(2\):

\ [\ begin {align} <S_z>&=\ frac {1} {2}\ frac {\ izquierda |\ sombrero {E} _ {1}\ derecha |^ {2}} {\ eta _ {1}} =\ frac {1} {2}\ frac {\ izquierda |\ sombrero {E} _ {2}\ derecha |^ {2}} {\ eta _ {2}}\ umber\\ &
=\ frac {1} {2}\ textrm {Re}\ izquierda [\ izquierda (\ hat {E} _ {+} e^ {-jkd} +\ hat {E} _ {-} e^ {+jkd}\ derecha)\ frac {\ izquierda (\ hat {E} _ {+} ^ {\ ast} e^ {+ jkd} -\ hat {E} _ _ {-} ^ {\ ast} e^ {-jkd}\ derecha)} {\ eta}\ derecha]\ nonumber\\ &
=\ frac {1} {2\ eta}\ izquierda (\ izquierda |\ sombrero {E} _ {+}\ derecha |^ {2} -\ izquierda |\ sombrero {E} _ {-}\ derecha {2}\ derecha)\ end {align}\ nonumber\]

Tenga en cuenta que para un espesor de recubrimiento dado\(d\), no hay reflexión solo a frecuencias seleccionadas correspondientes a longitudes de onda\(d=n\lambda /4,\quad n=1,3,5,....\) Para una banda estrecha de longitudes de onda alrededor de estas longitudes de onda seleccionadas, las reflexiones son pequeñas. La permeabilidad magnética de los recubrimientos y del vidrio utilizado en los componentes ópticos suele ser la del espacio libre mientras que las permitividades difieren. Luego se escoge la permitividad del recubrimiento\(\varepsilon\) de manera que

\[ \varepsilon = \sqrt{\varepsilon _{2}\varepsilon _{0}} \nonumber \]

y con un espesor correspondiente al rango central de las longitudes de onda de interés (a menudo en lo visible).