7.7: Ondas Planas Uniformes y No Uniformes

Nuestro análisis hasta ahora se ha limitado a las ondas que se propagan en la\(z\) dirección que normalmente inciden sobre las interfaces del avión. Aunque nuestros ejemplos tuvieron el campo eléctrico polarizado en la\(x\) dirección., el procedimiento de solución es el mismo para la polarización del campo eléctrico\(y\) dirigido ya que ambas polarizaciones son paralelas a las interfaces de discontinuidad.

Propagación en un ángulo arbitrario

Consideramos ahora una onda plana uniforme con flujo de potencia en ángulo con respecto\(\theta \) al\(z\) eje, como se muestra en la Figura 7-16. Se supone que el campo eléctrico está\(y\) dirigido, pero el campo magnético que es perpendicular a ambos\(\textbf{E}\) y\(\textbf{S}\) ahora tiene componentes en las\(z\) direcciones\(x\) y.

La dirección del flujo de potencia, que podemos llamar\(z'\), está relacionada con las coordenadas cartesianas como

\[ z'=x\sin \theta +z\cos \theta  \nonumber \]

para que el factor de fase\(kz' \) pueda escribirse como

\ [\ begin {align} kz'=k_ {x} x+k_ {z} z,\ quad k_ {x} & =k\ sin\ theta\ nonumber\\
k_ {z} &=k\ cos\ theta\ end {align}\ nonumber\]

donde la magnitud del número de onda es

\[ k=\omega \sqrt{\varepsilon \mu } \nonumber \]

Figura 7-16 La dependencia espacial de una onda plana uniforme en un ángulo arbitrario\(\theta \) puede expresarse en términos de un número de onda vectorial\(\textbf{k}\) como\(e^{-j\textbf{k}\cdot r}\), donde\(\textbf{k}\) está en la dirección del flujo de potencia y tiene magnitud\(\omega /c\).

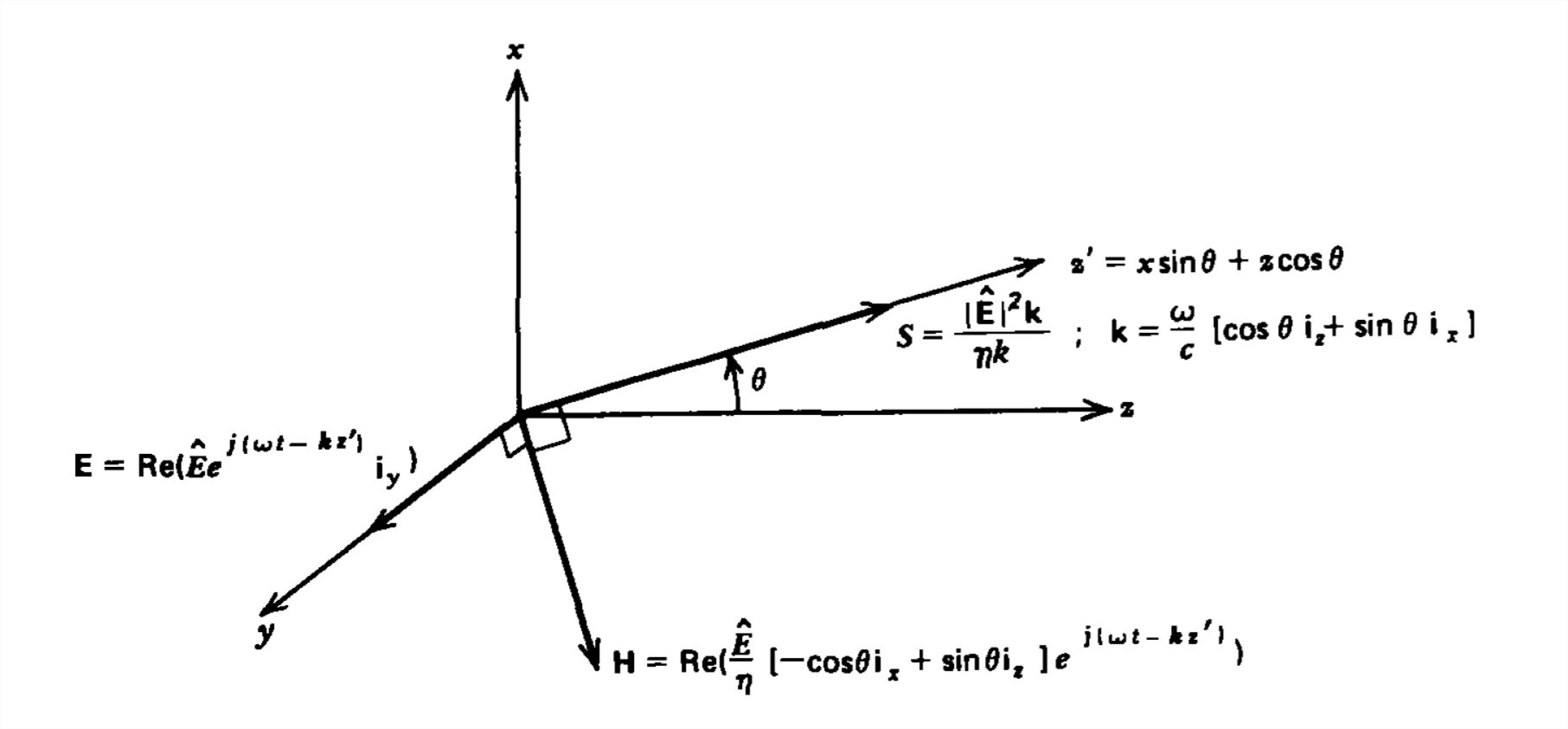
Esto nos permite escribir los campos como

\ [\ begin {align}\ textbf {E} & =\ textbf {Re}\ izquierda [\ hat {E} e^ {j\ izquierda (\ omega t-k_ {z} x-k_ {z} z\ derecha)\ textbf {i} _ {y}}\ derecha]\ nonumber\
\ textbf {H} & =\ textbf {Re} izquierda [\ frac {\ sombrero {E}} {\ eta}\ izquierda (-\ cos\ theta\ textbf {i} _ {x} +\ sin\ theta\ textbf {i} _ {z}\ derecha) e^ {j\ izquierda (\ omega t-k_ {z} x-k_ {z} } z\ derecha)}\ derecha]\ end {align}\ nonumber\]

Observamos que la dependencia espacial de los campos se puede escribir como\(e^{-j\textbf{k}\cdot r}\), donde el número de onda se trata como un vector:

\[ \textbf{k}=k_x \textbf{i}_x+k_y \textbf{i}_y+k_z \textbf{i}_z \nonumber \]

con

\[ \textbf{r}=x\textbf{i}_x+y\textbf{i}_y+z\textbf{i}_z \nonumber \]

para que

\[ \textbf{k}\cdot \textbf{r}=k_x x+k_y y+k_z z \nonumber \]

La magnitud de\(\textbf{k}\) es como se da en (3) y su dirección es la misma que el flujo de potencia\(\textbf{S}\):

\ [\ begin {align}\ textbf {S} &=\ textbf {E}\ veces\ textbf {H} =\ frac {\ izquierda |\ hat {E}\ derecha |^ {2}} {\ eta}\ izquierda (\ cos\ theta\ textbf {i} _ {z} +\ sin\ theta\ textbf {i} _ {x}\ derecha)\ cos ^ {2}\ izquierda (\ omega t-\ textbf {k}\ cdot\ textbf {r}\ derecha)\ nonumber\\ &
=\ frac {\ izquierda |\ sombrero {E}\ derecha |^ {2}\ textbf {k}} { \ omega\ mu}\ cos ^ {2}\ izquierda (\ omega t-\ textbf {k}\ cdot\ textbf {r}\ derecha)\ end {align}\ nonumber\]

donde sin pérdida de generalidad escogimos la fase de ser cero\(\hat{E}\) para que sea real.

La constante de propagación compleja

Generalicemos más considerando campos de la forma

\ [\ begin {align}
\ textbf {E} &=\ textrm {Re}\ izquierda [\ hat {\ textbf {E}} e^ {j\ omega t} e^ {-\ negridsymbol {\ gamma}\ textbf {r}}\ derecha] =
\ textrm {Re}\ izquierda [\ hat {\ textbf {E}} e^ {j\ izquierda (\ omega t-\ textbf {k}\ cdot\ textbf {r}\ derecha)} e^ {-\ boldsymbol {\ alpha}\ cdot\ textbf {r}}\ derecha]\ nonumber\\
\ textbf {H} & =\ textrm {Re}\ izquierda [\ hat {\ textbf {H}} e^ {j\ omega t} e^ {-\ negridsymbol {\ gamma}\ textbf {r}}\ derecha] =
\ textrm {Re}\ izquierda [\ hat {\ textbf {H}} e^ {j\ izquierda (\ omega- t\ textbf {k}\ cdot\ textbf {r}\ derecha)} e^ {-\ boldsymbol {\ alpha}\ cdot\ textbf {r}}\ derecha]
\ end {align}\ nonumber\]

donde\(\boldsymbol{\gamma}\) es el vector de propagación complejo y\(\textbf{r}\) es el vector de posición de (6):

\ [\ begin {align}\ negridsymbol {\ gamma} &=\ negridsymbol {\ alpha} +j\ textbf {k} =\ gamma_ {x}\ textbf {i} _ {x} +\ gamma_ {y}\ textbf {i} _ {y} +\ gamma_ {z}\ textbf {i} _ {z}\ nonumbumber\\
\ negridsymbol {\ gamma}\ cdot\ textbf {r} &=\ gamma_ {x} x+\ gamma_ {y} y+\ gamma_ {z} z\ end {align}\ nonumber\]

Anteriormente hemos considerado ondas planas uniformes en medios sin pérdidas donde el número de onda\(\textbf{k}\) es puro real y\(z\) dirigido con\(\alpha=0\) lo que\(\boldsymbol{\gamma}\) es puro imaginario. El parámetro\(\boldsymbol{\alpha }\) representa la tasa de decaimiento de los campos aunque el medio no tenga pérdidas. Si\(\boldsymbol{\alpha }\) es distinto de cero, las soluciones se denominan ondas planas no uniformes. Vimos esta decadencia en nuestras soluciones cuasiestáticas de la ecuación de Laplace donde las soluciones tenían oscilaciones en una dirección pero decaimiento en la dirección perpendicular. Esperaríamos que esta evanescencia se mantuviera en bajas frecuencias.

El valor de la forma asumida de soluciones en (9) es que el\(\textrm{del}\left ( \boldsymbol{\nabla}\right )\) operador en las ecuaciones de Maxwell puede ser reemplazado por el operador vectorial\(-\boldsymbol{\gamma}\):

\ [\ begin {align}\ boldsymbol {\ nabla} &=\ frac {\ parcial} {\ parcial} {\ parcial x}\ textbf {i} _ {x} +\ frac {\ parcial} {\ parcial y}\ textbf {i} _ {y} +\ frac {\ parcial} {\ parcial z}\ textbf {i} _ {z}\ nonumber\\ &
=-\ gamma_ {x}\ textbf {i} _ {x} -\ gamma_ {y}\ textbf {i} _ _ {y} -\ gamma_ {z}\ textbf {i} _ {z}\ nonumber\\ &
=- \ negridsymbol {\ gamma}\ end {align}\ nonumber\]

Esto es cierto porque cualquier derivada espacial solo opera sobre el término exponencial en (9). Entonces las ecuaciones de Maxwell libres de fuente pueden escribirse en términos de las amplitudes complejas como

\ [-\ negridsymbol {\ gamma}\ veces\ sombrero {\ textbf {E}} = -j\ omega\ mu\ sombrero {\ textbf {H}}\\
-\ negridsymbol {\ gamma}\ veces\ sombrero {\ textbf {H}} = j\ omega\ varepsilon\ sombrero {\ textbf {E}}\
-\ negritasímbolo {\ gamma}\ cdot\ varepsilon\ sombrero {\ textbf {E}} = 0\\
-\ negridsymbol {\ gamma}\ cdot\ sombrero {\ textbf {H}} = 0\ nonumber\]

Las dos últimas relaciones nos dicen que\(\boldsymbol{\gamma }\) es perpendicular a ambos\(\textbf{E}\) y\(\textbf{H}\). Si tomamos\(\boldsymbol{\gamma }\times \) la ecuación superior y usamos la segunda ecuación, tenemos

\[ \begin{align}-\boldsymbol{\gamma }\times \left ( \boldsymbol{\gamma }\times \hat{\textbf{E}} \right )&=-j\omega \mu \left ( \boldsymbol{\gamma }\times \hat{\textbf{H}} \right )=-j\omega \mu \left ( -j\omega \varepsilon \hat{\textbf{E}} \right )\nonumber \\ &=-\omega^{2}\mu \varepsilon \hat{\textbf{E}}\end{align} \nonumber \]

El producto de doble cruz se puede ampliar como

\[ \begin{align}-\boldsymbol{\gamma }\times \left ( \boldsymbol{\gamma }\times \hat{\textbf{E}} \right )&=-\boldsymbol{\gamma } \left ( \boldsymbol{\gamma }\cdot  \hat{\textbf{E}} \right )+\left ( \boldsymbol{\gamma }\cdot \boldsymbol{\gamma } \right )\hat{\textbf{E}}\nonumber \\ &=\left ( \boldsymbol{\gamma }\cdot \boldsymbol{\gamma } \right )\hat{\textbf{E}}=-\omega^{2}\mu \varepsilon \hat{\textbf{E}}\end{align} \nonumber \]

El\(\boldsymbol{\gamma }\cdot \hat{\textbf{E}}\) término es cero a partir de la tercera relación en (12). La relación de dispersión es entonces

\[ \boldsymbol{\gamma }\cdot \boldsymbol{\gamma } =\left ( \alpha ^{2}-k^{2}+2j\boldsymbol{\alpha} \cdot \textbf{k} \right )=-\omega ^{2}\mu \varepsilon  \nonumber \]

Para la solución, las partes real e imaginaria de (15) deben ser por separado iguales:

\ [\ alfa ^ {2} -k^ {2} =-\ omega ^ {2}\ mu\ varepsilon\\
\ símbolo en negrilla {\ alfa}\ cdot\ textbf {k} =0\ nonumber\]

Cuando\(\boldsymbol{\alpha}=0\), (16) reduce a la relación frecuencia-número de onda familiar de la Sección 7-3-4.

La última relación nos dice ahora que la evanescencia (decaimiento) en el espacio como se representa por\(\boldsymbol{\alpha}\) está permitida por las ecuaciones de Maxwell, pero debe ser perpendicular a la propagación representada por\(\textbf{k}\).

Podemos calcular el flujo de potencia promedio en el tiempo para campos de la forma de (9) usando (12) en términos de cualquiera\(\hat{\textbf{E}}\) o de la\(\hat{\textbf{H}}\) siguiente manera:

\ [\ begin {align &= <\ textbf {S} >\ frac {1} {2}\ textrm {Re}\ izquierda (\ hat {\ textbf {E}}\ veces\ hat {\ textbf {H}} ^ {\ ast}\ derecha)\ nonumber\\ & =
-\ frac {1} {2}\ textrm {Re}\ izquierda (\ hat {\ tbtbf f {E}}\ veces\ frac {\ negridsymbol {\ gamma} ^ {\ ast}\ veces\ sombrero {\ textbf {E}} ^ {\ ast}} {j\ omega\ mu}\ derecha)\ nonumber\\ &
=-\ frac {1} {2}\ textrm {Re}\ izquierda (\ frac {\ negridsymbol {\ gamma} ^ {\ ast}\ izquierda |\ hat {\ textbf {E}}\ derecha |^ {2} -\ hat {\ textbf {E}} ^ {\ ast}\ left (\ negridsymbol {\ gamma} ^ {ast\}\ cdot\ sombrero {\ textbf {E}}\ derecha)} {j\ omega\ mu}\ derecha)\ nonumber\\ &
=\ frac {1} {2}\ frac {\ textbf {k}} {\ omega\ mu}\ izquierda |\ hat {\ textbf {E}}\ derecha |^ {2} +\ frac {1} {2}\ textrm {Re}\ left (\ frac {\ hat {\ textbf {E}} ^ {\ ast}\ left (\ negridsymbol {\ gamma} ^ {\ ast}\ cdot\ hat {\ textbf {E}\ right)} {j\ omega\ mu}\ derecha)\ nonumber\\ &=
<\ textbf {S} >\ frac {1} {2}\ textrm {Re}\ left (\ hat {\ textbf {E}}\ times\ hat {\ textbf {H}} ^ {\ ast} \ derecha)\ nonumber\\ &
=-\ frac {1} {2}\ textrm {Re}\ izquierda (\ frac {\ izquierda (\ negritasímbolo {\ gamma}\ veces\ sombrero {\ textbf {H}}\ derecha)} {j\ omega\ varepsilon}\ veces\ sombrero {\ textbf {H}} ^ {\ ast} derecha)\ nonumber\\ &
=\ frac {1} {2}\ textrm {Re}\ izquierda (\ frac {\ negritasímbolo {\ gamma}\ izquierda |\ sombrero {\ textbf {H}}\ derecha |^ {2} -\ hat {\ textbf {H}} ^ {\ ast}\ izquierda (\ negridsymbol {\ gamma}\ cdot\ hat {\ textbf {H}} ^ {\ ast}\ derecha)} {j\ omega\ varepsilon}\ derecha)\ nonumber\\ &
=\ frac {1} {2} frac {\ textbf {k}} {\ omega\ varepsilon}\ izquierda |\ sombrero {\ textbf {H}}\ derecha |^ {2} -\ frac {1} {2}\ textrm {Re}\ izquierda (\ frac {\ sombrero {\ textbf {H}} \ left (\ negridsymbol {\ gamma}\ cdot\ hat {\ textbf {H}} ^ {\ ast}\ derecha)} {j\ omega\ varepsilon}\ derecha)
\ end {align}\ nonumber\]

Aunque ambas expresiones finales en (17) son equivalentes, es conveniente escribir el flujo de potencia en términos de cualquiera\(\hat{\textbf{E}}\) o\(\hat{\textbf{H}}\). Cuando\(\hat{\textbf{E}}\) es perpendicular a ambos vectores reales\(\boldsymbol{\alpha }\) y\(\boldsymbol{\beta }\), definido en (10) y (16), el producto punto\(\boldsymbol{\gamma }^{\ast }\cdot \hat{\textbf{E}}\) es cero. Tal modo se llama eléctrico transversal (TE), y vemos en (17) que el flujo de potencia promedio en el tiempo sigue en la dirección del número de onda\(\textbf{k}\). De igual manera, cuando\(\textbf{H}\) es perpendicular a\(\boldsymbol{\alpha }\) y\(\boldsymbol{\beta }\), el producto punto\(\boldsymbol{\gamma }\cdot \hat{\textbf{H}}^{\ast }\) es cero y tenemos un modo magnético transversal (TM). Nuevamente, el flujo de potencia promedio en el tiempo en (17) está en la dirección de\(\textbf{k}\). La magnitud de\(\textbf{k}\) está relacionada con\(\omega\) en (16).

Tenga en cuenta que nuestra discusión se ha limitado a los sistemas sin pérdidas. Podemos incluir pérdidas óhmicas si reemplazamos\(\varepsilon\) por la permitividad compleja\(\hat{\varepsilon }\) de la Sección 7-4-3 en (15) y (17). Entonces, siempre hay decaimiento\((a\neq 0)\) por disipación óhmica (ver Problema 22).

Ondas Planas No Uniformes

Podemos examinar soluciones de ondas planas no uniformes con valores distintos\(\boldsymbol{\alpha }\) de cero considerando una hoja actual en el\(z =0\) plano, que es una onda viajera en la\(x\) dirección:

\[ K_{x}\left ( z= 0 \right )= K_{0}\cos \left ( \omega t-k_{x}x \right )=\textrm{Re}\left ( K_{0}e^{j\left ( \omega t-k_{x}x \right )} \right ) \nonumber \]

La corriente superficial\(x\) dirigida da lugar a un campo magnético\(y\) dirigido. Debido a que el sistema no depende de la\(y\) coordenada, las soluciones son así de la siguiente forma:

\ [H_ {y} =\ izquierda\ {\ comenzar {matriz}
\ textrm {Re}\ izquierda (\ hat {H} _ {1} e^ {j\ omega t} e^ {-\ negridsymbol {\ gamma} _ {1}\ cdot\ textbf {r}}\ derecha),\ quad z> 0\
\ textrm {Re}\ izquierda (\ sombrero {H} _ {2} e^ {j\ omega t} e^ {-\ negridsymbol {\ gamma} _ {2}\ cdot\ textbf {r}}\ derecha),\ quad z< 0
\ end {matriz}\ a la derecha. \\
\ textbf {E} =\ izquierda\ {\ comenzar {matriz}
\ textrm {Re}\ izquierda [-\ frac {\ negritasímbolo {\ gamma} _ {1}\ veces\ sombrero {H} _ {1}} {j\ omega\ varepsilon}\ textbf {i} _ {y} e^ {j\ omega t} e^ {-\ bolddsymbol {\ gamma} _ {1}\ cdot\ textbf {r}}\ derecha],\ quad z> 0\\
\ textrm {Re}\ izquierda [-\ frac {\ negritasímbolo {\ gamma } _ {2}\ veces\ sombrero {H} _ {2}} {j\ omega\ varepsilon}\ textbf {i} _ {y} e^ {j\ omega t} e^ {-\ negridsymbol {\ gamma} _ {2}\ cdot\ textbf {r}}\ derecha],\ quad z< 0
\ end {matriz}\ derecha. \ nonumber\]

donde\(\boldsymbol{\gamma }_{1}\) y\(\boldsymbol{\gamma }_{2}\) son los vectores de propagación complejos en cada lado de la hoja actual:

\ [\ negridsymbol {\ gamma} _ {1} =\ gamma _ {1x}\ textbf {i} _ {x} +\ gamma _ {1z}\ textbf {i} _ {z}\\ símbolo en negrilla {
\ gamma} _ {2} =\ gamma _ {2x}\ textbf {i} _ {x} +\ gamma _ {2z}\ textbf {i} _ {x} +\ gamma _ {2z}\ tbtbf f {i} _ {z}\ nonumber\]

La condición límite de la discontinuidad de tangencial\(\textbf{H}\) al\(z =0\) igualar los rendimientos de corriente superficial

\[ -\hat{H}_{1}e^{-\boldsymbol{\gamma }_{1x}x}+\hat{H}_{2}e^{-\boldsymbol{\gamma }_{2x}x}=K_{0}e^{-jk_{x}x} \nonumber \]

que nos dice que los\(x\) componentes de los vectores de propagación complejos equivalen a la dependencia espacial trigonométrica de la corriente superficial:

\[ \gamma_{1x}+\gamma_{2x}=jk_{x} \nonumber \]

Los\(z\) componentes de\(\boldsymbol{\gamma }_{1}\) y luego\(\boldsymbol{\gamma }_{2}\) se determinan a partir de (15) como

\[ \gamma_{x}^{2}+\gamma_{z}^{2}=-\omega ^{2}\varepsilon \mu \Rightarrow \gamma _{z}=\pm \left ( k_{x}^{2}-\omega ^{2}\varepsilon \mu  \right )^{1/2} \nonumber \]

Si\(k_{x}^{2}<\omega ^{2}\varepsilon \mu\),\(\gamma _{z}\) es puro imaginario que representa la propagación y tenemos ondas planas uniformes. Si\(k_{x}^{2}>\omega ^{2}\varepsilon \mu\), entonces\(\gamma _{z}\) es puro real representando evanescencia en la\(z\) dirección para que generemos ondas planas no uniformes. Cuando\(w =0\), (23) corresponde a soluciones laplacianas que oscilan en la\(x\) dirección pero decaen en la\(z\) dirección.

El\(z\) componente de\(\boldsymbol{\gamma }\) es de signo opuesto en cada región,

\[ \gamma _{1z}=-\gamma _{2z}=+\left ( k_{x}^{2}-\omega ^{2}\varepsilon \mu \right )^{1/2} \nonumber \]

a medida que las ondas se propagan o decaen lejos de la lámina. Continuidad del componente tangencial de\(\textbf{E}\) requiere

\[ \gamma _{1z}\hat{H}_{1}=-\gamma _{2z}\hat{H}_{2}\Rightarrow \hat{H}_{2}=-\hat{H}_{1}=K_{0}/2 \nonumber \]

Si\(k_{x}=0\), volvemos a obtener la solución de la Sección 7-4-1. Incrementando\(k_{x}\). genera ondas propagadoras con flujo de potencia en las\(k_{x}\textbf{i}_{x}\pm k_{z}\textbf{i}_{z}\) direcciones. En\(k_{x}^{2}=\omega ^{2}\varepsilon \mu ,\,k_{z}= 0\) para que el flujo de potencia se\(x\) dirija puramente sin dependencia espacial de\(z\). El aumento adicional se\(k_{x}\) convierte\(k_{z}\) a\(\alpha _{z}\) lo que\(\gamma _{z}\) se vuelve real y los campos se descomponen con\(z\).