7.8: Incidencia oblicua sobre un conductor perfecto

E Campo Paralelo a la Interfaz

En la Figura 7-17a se muestra una onda plana uniforme incidente sobre un conductor perfecto con flujo de potencia en ángulo\(\theta _{i}\) con la normal. El campo eléctrico es paralelo a la superficie con el campo magnético que tiene ambos\(x\) y\(z\) componentes:

\ [\ textbf {E} _ _ {i} =\ textrm {Re}\ izquierda [\ hat {E} _ {i} e^ {j\ izquierda (\ omega t-k_ {xi} x-k_ {zi} z\ derecha)}\ textbf {i} _ {y}\ derecha]\
\ textbf {H} _ _ {i} =\ textrm {Re}\ left [\ frac {\ hat {E} _ {i}} {\ eta}\ left (-\ cos\ theta _ {i}\ textbf {i} _ {x} +\ sin\ theta _ {i}\ textbf {i} _ {z}\ derecha) e^ {j\ izquierda (\ omega t-k_ {xi} x-k_ {zi} z\ derecha)}\ derecha]\ nonumber\]

donde

\ [\ izquierda. \ begin {matriz}
k_ {xi} =k\,\ sin\ theta_ {i}\\
k_ {zi} =k\,\ cos\ theta_ {i}\ end {matriz}\ derecha\}\ quad k=\ omega\ sqrt {\ varepsilon\ mu},\ quad\ eta =\ sqrt {\ frac {\ mu} {\ epsilon\ mu},\ quad\ eta =\ sqrt {\ frac {\ mu} {epsilon\ mu} on}}\ nonumber\]

Figura 7-17 Una onda plana uniforme que incide oblicuamente sobre un conductor perfecto tiene su ángulo de incidencia igual al ángulo de reflexión. a) Campo eléctrico polarizado paralelo a la interfaz. b) Campo magnético paralelo a la interfaz.

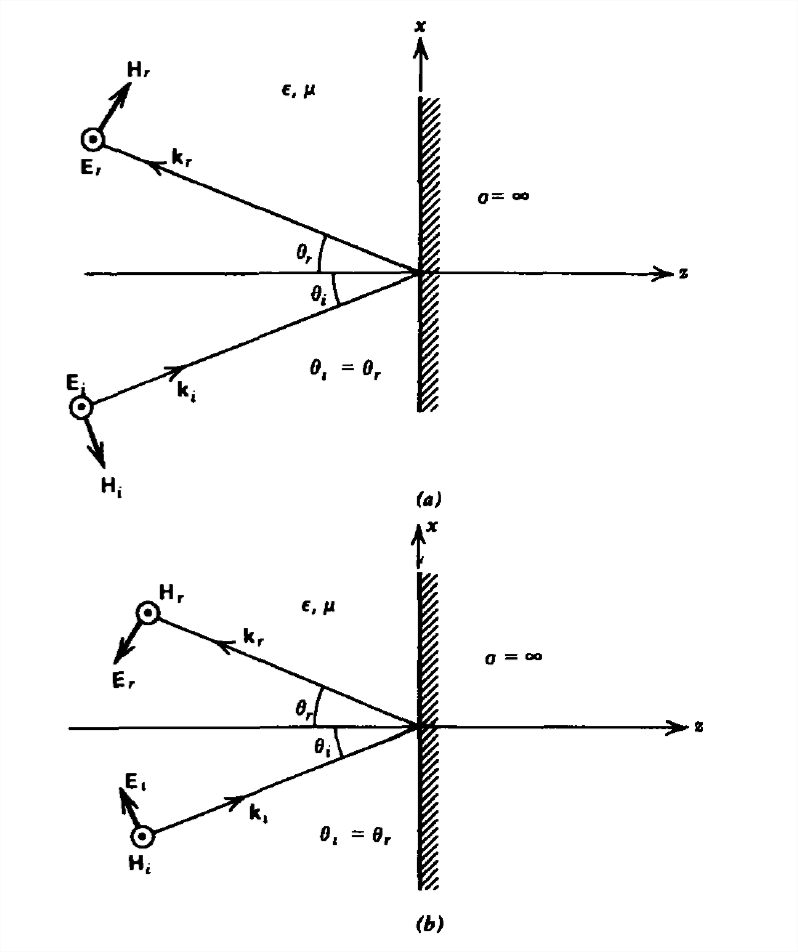
No hay campos transmitidos dentro del conductor perfecto, pero hay un campo reflejado con flujo de potencia en ángulo\(\theta _{r}\) desde la interfaz normal. El campo eléctrico reflejado también está en la\(y\) dirección por lo que el campo magnético, que debe ser perpendicular a ambos\(\textbf{E}\) y\(\textbf{S}=\textbf{E}\times \textbf{H}\), está en la dirección que se muestra en la Figura 7-17a:

\ [\ textbf {E} _ _ {r} =\ textrm {Re}\ izquierda [\ hat {E} _ {r} e^ {j\ izquierda (\ omega t-k_ {xr} x+k_ {zr} z\ derecha)}\ textbf {i} _ _ {y}\ derecha]
\\ textbf {H} _ {r} =\ textrm {Re}\ izquierda [\ frac {\ hat {E} _ {r}} {\ eta}\ izquierda (\ cos\ theta _ {r}\ textbf {i} _ {x} +\ sin\ theta _ {r}\ textbf {i} _ {z}\ derecha) e^ {j\ izquierda (omega t-k_ {xr} x+k_ {zr z}\ derecha)}\ derecha]\ nonumber\]

donde están los onumerosreflejados

\ [k_ {xr} =k\,\ sin\ theta_ {r}\\
k_ {zr} =k\,\ cos\ theta_ {r}\ nonumber\]

En este punto desconocemos el ángulo de reflexión\(\theta_{r}\) o la amplitud reflejada\(\hat{E}_{r}\). Se determinarán a partir de las condiciones límite a\(z =0\) de continuidad de tangencial\(\textbf{E}\) y normal\(\textbf{B}\). Debido a que no hay campos dentro del conductor perfecto, estas condiciones de límite\(z =0\) son

\ [\ begin {align}\ hat {E} _ {i} e^ {-jk_ {xi} x} +\ hat {E} _ {r} e^ {-jk_ {xr} x} & =0\ nonumber\
\ frac {\ mu} {\ eta}\ left (\ hat {E} _ {i}\ sin\ theta _ {i} e^ {-jk_ {xi} x} +\ hat {E} _ _ {r}\ sin\ theta _ {r} e^ {-jk_ {xr} x}\ derecha) &=0\ end {align}\ nonumber\]

Estas condiciones deben ser ciertas para cada valor de\(x\) lo largo de\(z = 0\) manera que los factores de fase dados en (2) y (4) deben ser iguales,

\[ k_{xi}=k_{xr}\Rightarrow \theta _{i}=\theta _{r}\equiv \theta  \nonumber \]

dando la conocida regla de que el ángulo de incidencia es igual al ángulo de reflexión. La amplitud del campo reflejado es entonces

\[ \hat{E}_{r}=-\hat{E}_{i} \nonumber \]

siendo redundantes las condiciones límite en (5) ya que ambas ceden (7). Los campos totales son entonces:

\ [\ begin {align} E_ {y} &=\ textrm {Re}\ izquierda [\ hat {E} _ _ {i}\ izquierda (e^ {-jk_ {z} z} -e^ {+jk_ {z} z}\ derecha) e^ {j\ izquierda (\ omega t-k_ {z} x\ derecha)}\ nonumber\ &
=2E_ {i}\ sin k_ {z} z\ sin\ izquierda (\ omega t-k_ {x} x\ derecha)\ nonumber\\
\ textbf {H} &=\ textrm {Re}\ izquierda [\ frac {\ sombrero {E} _ _ {i }} {\ eta}\ izquierda [\ cos\ theta\ izquierda (-e^ {-jk_ {z} z} -e^ {+jk_ {z} z}\ derecha)\ textbf {i} _ _ {x} +\ sin\ theta\ izquierda (e^ {-jk_ {z} z} -e^ {+jk_ {z} z}\ derecha)\ textbf {i} _ {z}\ derecha] e^ {j\ izquierda (\ omega t-k_ {z} x\ derecha)}\ derecha]\ nonumber\\ &
=\ frac {2E_ {i}} {\ eta}\ izquierda [-\ cos\ theta\ cos k_ {z} z\ cos\ izquierda (\ omega t-k_ {x} x\ derecha)\ textbf {i} _ {x} +\ sin\ theta\ sin k_ {z} z\ sin\ izquierda (\ omega t-k_ {x} x\ derecha)\ textbf {i} _ _ {z}\ derecha]\ end {align}\ nonumber\]

donde sin pérdida de generalidad tomamos\(\hat{E}_{i}\) para ser reales.

Dejamos caer los\(r\) subíndices\(i\) y en los numeros de onda y ángulos porque son iguales. Los campos viajan en\(x\) dirección paralela a la interfaz, pero son estacionarios en la\(z\) dirección. Tenga en cuenta que otro plano perfectamente conductor se puede colocar a distancias\(d\) a la izquierda de la interfaz en

\[ k_{z}d=n\pi  \nonumber \]

donde el campo eléctrico ya es cero sin perturbar las soluciones de (8). Las condiciones de contorno en el segundo conductor se satisfacen automáticamente. Tal estructura se denomina guía de ondas y se discute en la Sección 8-6.

Debido a que el componente tangencial de\(\textbf{H}\) es discontinuo en\(z =0\), una corriente superficial de onda viajera fluye a lo largo de la interfaz,

\[ K_{y}=-H_{x}\left ( z=0 \right )=\frac{2E_{i}}{\eta }\cos \theta \cos \left ( \omega t-k_{x}x \right ) \nonumber \]

A partir de (8) calculamos el flujo de potencia promedio en el tiempo como

\ [\ begin {align &= <\ textbf {S} >\ frac {1} {2}\ textrm {Re}\ left [\ hat {\ textbf {E}}\ left (x, z\ right)\ times\ hat {\ textbf {H}} ^ {\ ast}\ left (x, z\ right)\ right]\ nonumber\\ & =
\ frac {2E_ {i} ^ {2}} {\ eta}\ sin\ theta\ sin ^ {2} k_ {z} z\ textbf {i} _ _ {x}\ end {align}\ nonumber\]

Vemos que el único flujo de potencia distinto de cero está en la dirección paralela al límite interfacial y varía en función de\(z\).

Campo H Paralelo a la Interfaz

Si el\(\textbf{H}\) campo es paralelo al límite conductor, como en la Figura 7-17b, los campos incidente y reflejado son los siguientes:

\ [\ begin {align}\ textbf {E} _ {i} &=\ textrm {Re}\ left [\ hat {E} _ {i}\ left (\ cos\ theta _ {i}\ textbf {i}\ textbf {i} _ {x} -\ sin\ theta _ {i}\ textbf {i} _ {z}\ derecha) e^ {j\ izquierda (\ omega t-k_ {xi} x-k_ {zi} z\ derecha)}\ derecha]\ nonumber
\\ textbf {H} _ {i} &=\ textrm {Re}\ izquierda [\ frac {\ sombrero {E} _ {i}} {\ eta} e^ {j\ izquierda (\ omega t- k_ {xi} x-k_ {zi} z\ derecha)}\ textbf {i} _ {y}\ derecha]\ nonumber\
\ textbf {E} _ {r} &=\ textrm {Re}\ izquierda [\ hat {E} _ {r}\ izquierda (-\ cos\ theta _ {r}\ textbf {i} _ {x} -\ sin\ theta _ {r}\ textbf {i} _ _ {z}\ derecha) e^ {j\ izquierda (\ omega t-k_ {xr} x+k_ {zr} z\ derecha)}\ derecha]\ nonumber\
\ textbf {H} _ _ {r} &=\ textrm {Re}\ izquierda [\ frac {\ sombrero {E} _ {r}} {\ eta} e^ {j\ izquierda (\ omega t-k_ {xr} x+k_ {zr} z\ derecha)}\ textbf {i} _ {y}\ derecha]\ end {align}\ nonumber\]

El componente tangencial de\(\textbf{E}\) es continuo y por lo tanto cero en\(z = 0\):

\[  \hat{E}_{i}\cos \theta _{i}e^{-jk_{xi}x}-\hat{E}_{r}\cos \theta _{r}e^{-jk_{xr}x}=0 \nonumber \]

No hay componente normal de\(\textbf{B}\). Esta condición límite debe ser satisfecha para todos los valores de\(x\) por lo que nuevamente el ángulo de incidencia debe ser igual al ángulo de reflexión\(\left ( \theta _{i}=\theta _{r} \right )\) para que

\[ \hat{E}_{i}=\hat{E}_{r} \nonumber \]

El total\(\textbf{E}\) y\(\textbf{H}\) los campos se pueden obtener de (12) sumando los campos incidentes y reflejados y tomando la parte real;

\ [\ begin {align}\ textbf {E} &=\ textrm {Re}\ izquierda [\ hat {E} _ {i}\ izquierda [\ cos\ theta\ izquierda (e^ {-jk_ {z} z} -e^ {+jk_ {z} z}\ derecha)\ textbf {i} _ {x} -\ sin\ theta\ izquierda (e^ {-jk_ {z} z} +e^ {+jk_ {z} z}\ derecha)\ textbf {i} _ {z}\ derecha] e^ {j\ izquierda (\ omega t-k_ {z} x\ derecha)}\ derecha]\ nonumber\\ &
=2E_ {i}\ izquierda [\ cos\ theta\ sin k_ {z} z\ sin\ izquierda (\ omega t-k_ {x} x\ derecha)\ textbf {i} _ {x} -\ sin\ theta\ cos k_ {z} z\ cos\ izquierda (\ omega t-k_ {x} x\ derecha)\ textbf {i} _ _ {z}
\ derecha]\ nonumber
\\ tbf {H} &=\ textrm {Re}\ izquierda [\ frac {\ hat {E} _ {i}} {\ eta}\ izquierda (e^ {-jk_ {z} z} +e^ {+jk_ {z} z}\ derecha) e^ {j\ izquierda ( \ omega t-k_ {z} x\ derecha)}\ textbf {i} _ {y}\ derecha]\ nonumber\\ &
=\ frac {2E_ {i}} {\ eta}\ cos k_ {z} z\ cos\ izquierda (\ omega t-k_ {x} x\ derecha)\ textbf {i} _ _ {y}
\ end {align}\ nonumber\ er\]

La corriente superficial en la superficie conductora en\(z =0\) viene dada por el componente tangencial de\(\textbf{H}\)

\[  K_{y}\left ( z=0 \right )=H_{y}\left ( z=0 \right )=\frac{2E_{i}}{\eta }\cos \left ( \omega t-k_{x}x \right ) \nonumber \]

mientras que la carga superficial\(z = 0\) es proporcional al componente normal del campo eléctrico,

\[ \sigma _{f}\left ( z=0 \right )=-\varepsilon E_{z}\left ( z=0 \right )=2\varepsilon E_{i}\sin \theta \cos \left ( \omega t-k_{x}x \right ) \nonumber \]

Obsérvese que (16) y (17) satisfacen la conservación de la corriente en la superficie conductora,

\[ \nabla _{\Sigma }\cdot \textbf{K}+\frac{\partial \sigma _{f}}{\partial t}=0\Rightarrow \frac{\partial K_{x}}{\partial x}+\frac{\partial \sigma _{f}}{\partial t}=0 \nonumber \]

donde

\[ \nabla _{\Sigma }=\frac{\partial }{\partial x}\textbf{i}_{x}+\frac{\partial }{\partial y}\textbf{i}_{y} \nonumber \]

es el operador de divergencia superficial. El flujo de potencia promedio en el tiempo para esta polarización también se\(x\) dirige:

\ [\ begin {align &= <\ textbf {S} >\ frac {1} {2}\ textrm {Re}\ izquierda [\ hat {\ textbf {E}}\ veces\ hat {\ textbf {H}} ^ {\ ast}\ derecha]\ nonumber\\ & =
\ frac {2E_ {i} ^ {2}} {eta\}\ sin\ theta\ cos ^ {2} k_ {z} z\ textbf {i} _ _ {x}\ end {align}\ nonumber\]