7.9: Incidencia oblicua sobre un dieléctrico
- Page ID
- 86855
\(E\)Paralelo a la interfaz
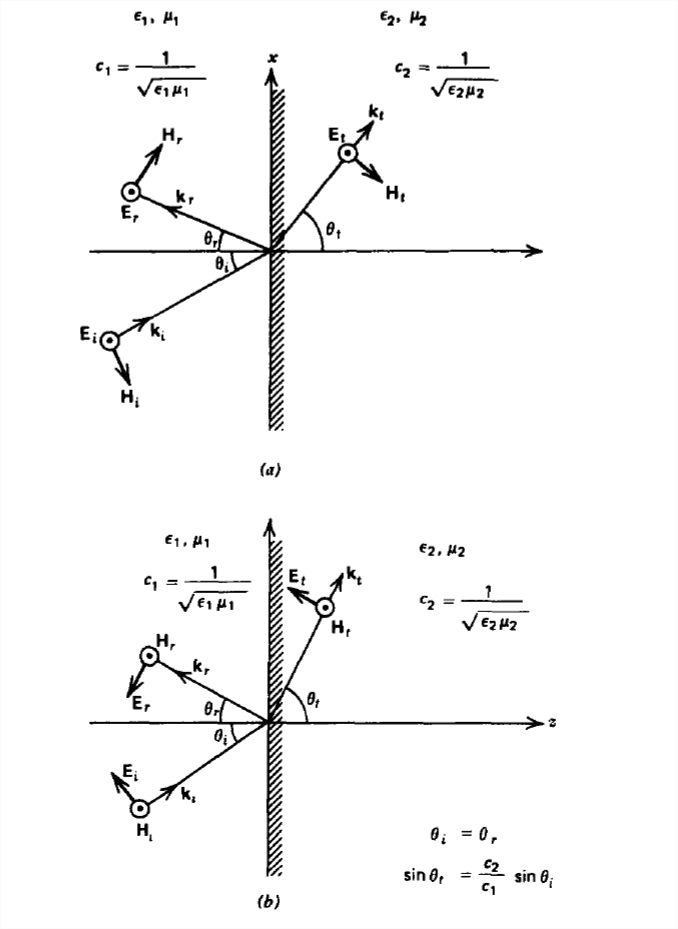
Una onda plana incidente sobre una interfaz dieléctrica, como en la Figura 7-18a, ahora tiene campos transmitidos así como campos reflejados. Para el campo eléctrico polarizado paralelo a la interfaz, los campos en cada región se pueden expresar como
\ [\ begin {align}\ textbf {E} _ {i} &=\ textrm {Re}\ left [\ hat {E} _ {i} _ {i} e^ {j\ left (\ omega t-k_ {xi} x-k_ {zi} z\ derecha)}\ textbf {i} _ {y}\ derecha]\ nonumber
\\ textbf {H} _ _ i} &=\ textrm {Re}\ left [\ frac {\ hat {E} _ {i}} {\ eta_ {1}}\ left (-\ cos\ theta _ {i}\ textbf {i} _ {x} +\ sin\ theta _ {i}\ textbf {i} _ _ {z}\ derecha) e^ {j\ izquierda (\ omega t-k_ {xi} x-k_ {zi} z\ derecha)}\ derecha]\ nonumber\
\ textbf {E} _ _ {r} &=\ textrm {Re}\ izquierda [\ hat {E} _ {r} e^ {j\ izquierda (\ omega t-k_ {xr} x+k_ {zr} z\ derecha)}\ textbf {i} _ {y}\ derecha]\ nonumber\
\ textbf {H} _ {r} &=\ textrm {Re}\ izquierda [\ frac {\ hat {E} _ {r}} {\ eta_ {2}}\ izquierda (\ cos\ theta _ {r}\ textbf {i} _ {x} +\ sin\ theta _ {r}\ textbf {i} _ {z}\ derecha) e^ {j\ izquierda (\ omega t-k_ {xr} x+k_ {zr} z\ derecha)}\ derecha]
\ nonumber\
\ textbf {E} _ {t} &=\ textrr m {Re}\ izquierda [\ hat {E} _ {t} e^ {j\ izquierda (\ omega t-k_ {xt} x-k_ {zt} z\ derecha)}\ textbf {i} _ {y}\ derecha]\ nonumber\
\ textbf {H} _ {t} &=\ textrm {Re}\ izquierda [\ frac {\ sombrero {E} _ {t}} {\ eta_ {3}}\ izquierda (-\ cos\ theta _ {t}\ textbf {i} _ {x} +\ sin\ theta _ {t}\ textbf {i} _ {z}\ derecha) ^ {j\ izquierda (\ omega t-k_ {xt} x-k_ {zt} z\ derecha)}\ derecha]\ end {align}\ nonumber\]
donde\(\theta _{i}\)\(\theta _{r}\), y\(\theta _{t}\) son los ángulos con respecto a la normalidad del incidente, los flujos de potencia reflejados y transmitidos. Los números de onda en cada región son
\ [k_ {xi} =k_ {1}\ sin\ theta _ {i},\ quad k_ {xr} =k_ {1}\ sin\ theta _ {r},\ quad k_ {xt} =k_ {2}\ sin\ theta _ {t}\\
k_ {zi} =k_ {1}\ sin\ theta _ {i},\ k_ {zr} =k_ {1}\ sin\ theta _ {r},\ quad k_ {zt} =k_ {2}\ sin\ theta _ {t}\ nonumber\]
donde están las magnitudes del número de onda, las velocidades de onda y las impedancias de onda
\ [k_ {1} =\ frac {\ omega} {c_ {1}},\ cuádruple k_ {2} =\ frac {\ omega} {c_ {2}},\ quad c_ {1} =\ frac {1} {\ sqrt {\ varepsilon _ {1}\ mu _ {1}}}
\\ eta _ {1} = sqrt rt {\ frac {\ mu _ {1}} {\ varepsilon _ {1}},\ quad\ eta _ {2} =\ sqrt {\ frac {\ mu _ {2}} {\ varepsilon _ {2}},\ quad c_ {2} =\ frac {1} {\ sqrt {\ varepsilon _ {2}\ mu _ {2}}}\ nonumber\]
Los ángulos y amplitudes desconocidos en (1) se encuentran a partir de las condiciones límite de continuidad de tangencial\(\textbf{E}\) y\(\textbf{H}\) en la\( z =0\) interfaz.
\ [\ sombrero {E} _ {i} e^ {-jk_ {xi} x} +\ sombrero {E} _ {r} e^ {-jk_ {xr} x} =\ sombrero {E} _ _ {t} e^ {-jk_ {xt} x}\
\ frac {-\ sombrero {E} _ _ {i}\ cos\ theta _ {i} ^ {-jk_ {xi} x} +\ sombrero {E} _ {r}\ cos\ theta _ {r} e^ {-jk_ {xr} x}} {\ eta _ {1}} =-\ frac {\ sombrero {E} _ {t}\ cos\ theta _ {t} e^ {-jk_ {xt} x} {\ eta_ {2}}\ nonumber\]
Estas condiciones de contorno deben cumplirse punto por punto para todos\(x\). Esto requiere que los factores exponenciales también sean
iguales para que los\(x\) componentes de todos los números de onda sean iguales,
\[ k_{xi}=k_{xr}=k_{xt}\Rightarrow k_{1}\sin \theta _{i}=k_{1}\sin \theta _{r}=k_{2}\sin \theta _{t} \nonumber \]
que relaciona los ángulos como
\ [\ theta _ {r} =\ theta _ {i}\\
\ sin\ theta _ {t} =\ izquierda (c_ {2} /c_ {1}\ derecha)\ sin\ theta _ {i}\ nonumber\]
Como antes, el ángulo de incidencia es igual al ángulo de reflexión. El ángulo de transmisión obedece a una relación más complicada llamada ley de Snell que relaciona los senos de los ángulos. El ángulo desde la normal es mayor en esa región que tiene la velocidad más rápida de las ondas electromagnéticas.
En óptica, la relación de la velocidad de la luz en vacío,\(c_{0}=1/\sqrt{\varepsilon_{0} \mu _{0}}\), a la velocidad de la luz en el medio se define como el índice de refracción,
\[ n_1=c_{0}/c_{1},\quad n_2=c_{0}/c_{2} \nonumber \]
que nunca es menos que la unidad. Entonces la ley de Snell se escribe como
\[ \sin \theta _{t}=\left ( n_{1}/n_{2} \right )\sin \theta _{i} \nonumber \]
Con los ángulos relacionados como en (6), las amplitudes de campo reflejadas y transmitidas pueden expresarse de la misma manera que para la incidencia normal (ver Sección 7-6-1) si reemplazamos las impedancias de onda por\(\eta \rightarrow \eta /\cos \theta \) para ceder
\ [R=\ frac {\ sombrero {E} _ {r}} {\ sombrero {E} _ _ {i}} =\ frac {\ frac {\ eta _ {2}} {\ cos\ theta _ {t}} -\ frac {\ eta _ {1}} {\ cos\ theta _ {i}}} {\ frac {\ eta _ {2}} {cos\ theta _ {t}} +\ frac {\ eta _ {1}} {\ cos\ theta _ {i}} =\ frac {\ eta _ {2}\ cos\ theta _ {i} -\ eta _ {1}\ cos\ theta _ {t}} {\ eta _ {2}\ cos\ theta _ {i} +\ cos\ theta _ {t}}\\
T=\ frac {\ sombrero {E} _ {t}} {\ sombrero {E} _ {i}} =\ frac {2\ eta _ {2}} {\ cos\ theta _ {t}\ izquierda (\ frac {\ eta _ {2}} {\ cos\ theta _ {t}} +\ frac {\ eta _ {1}} {\ cos\ theta _ {i}}\ derecha)} =\ frac {2\ eta _ {2}\ cos\ theta _ {i}} {\ eta _ {2}\ cos\ theta _ {i} +\ eta _ {1}\ cos\ theta _ {t}}\ nonumber\]
En (4) no consideramos la condición límite de continuidad de la normalidad\(\textbf{B}\) en\(z =0\). Esta condición de límite es redundante ya que es la misma condición que la ecuación superior en (4):
\[ \frac{\mu _{1}}{\eta _{1}}\left ( \hat{E}_{i}+\hat{E}_{r} \right )\sin \theta _{i}=\frac{\mu _{2}}{\eta _{2}} \hat{E}_{t}\sin \theta _{t}\Rightarrow \left ( \hat{E}_{i}+\hat{E}_{r} \right )=\hat{E}_{t} \nonumber \]
donde usamos la relación entre ángulos en (6). Desde
\[ \frac{\mu _{1}}{\eta _{1}}=\sqrt{\mu_{1} \varepsilon_{1}}=\frac{1}{c_{1}},\quad \frac{\mu _{2}}{\eta _{2}}=\sqrt{\mu_{2} \varepsilon_{2}}=\frac{1}{c_{2}} \nonumber \]
los términos trigonométricos en (11) cancelan debido a la ley de Snell. No hay ningún componente normal de\(\textbf{D}\) por lo que es automáticamente continuo a través de la interfaz.
Ángulo de no reflexión de Brewster
Vemos de (10) que en cierto ángulo de incidencia, no hay campo reflejado como\(R=0\). Este ángulo se llama ángulo de Brewster:
\[ R=0\Rightarrow \eta _{2}\cos \theta _{i}=\eta _{1}\cos \theta _{t} \nonumber \]
Al cuadrar (13), reemplazar los términos coseno por términos\(\left ( \cos ^{2}\theta =1-\sin ^{2}\theta \right )\) sinusoidales y usar la ley de Snell de (6), el ángulo Brewster\(\theta _{B}\) se encuentra como
\[ \sin ^{2}\theta_{B}=\frac{1-\varepsilon _{2}\mu _{1}/\left ( \varepsilon _{1}\mu _{2} \right )}{1-\left ( \mu _{1}/\mu _{2} \right )^{2}} \nonumber \]
No siempre hay una solución real para (14) ya que depende de las constantes materiales. El caso dieléctrico común, donde\(\mu_{1}=\mu_{2}\equiv \mu \) pero\(\varepsilon_{1}\neq \varepsilon_{2}\), no tiene solución ya que el lado derecho de (14) se vuelve infinito. Las soluciones reales para (14) requieren que el lado derecho esté entre cero y uno. El ángulo de un Brewster existe para la situación poco común donde\(\varepsilon_{1}= \varepsilon_{2}\) y\(\mu_{1}\neq \mu_{2}\):
\[ \sin ^{2}\theta _{B}=\frac{1}{1+\mu_{1}/\mu_{2}}\Rightarrow \tan \theta _{B}=\sqrt{\frac{\mu_{2}}{\mu_{1}}} \nonumber \]
En este ángulo de Brewster, los flujos de potencia reflejados y transmitidos están en ángulo recto\(\left ( \theta _{B}+\theta _{t}=\pi /2 \right )\) como se puede ver usando (6), (13) y (14):
\ [\ comenzar {alinear}\ cos\ izquierda (\ theta _ {B} +\ theta _ {t}\ derecha) &=\ cos\ theta _ {B}\ cos\ theta _ {t} -\ sin\ theta _ {B}\ sin\ theta _ {t}\ nonumber\\ &
=\ cos^ {2}\ theta _ {B}\ sqrt\ frac {\ mu _ {2}} {\ mu _ {1}} -\ sin^ {2}\ theta _ {B}\ sqrt {\ frac {\ mu _ {1}} {\ mu _ {2}}}\ nonumber\\ &
=\ sqrt {\ frac {\ frac { \ mu _ {2}} {\ mu _ {1}} -\ sin^ {2}\ theta _ {B}\ izquierda (\ sqrt {\ frac {\ mu _ {1}} {\ mu _ {2}}} +\ sqrt {\ frac {\ mu _ {2}} {\ mu _ {1}}\ derecha) =0
\ final {alinear}\ umber\]
Ángulo crítico de transmisión
La ley de Snell en (6) nos muestra que si\(c_{2}>c_{1}\), grandes ángulos de ángulo incidente\(\theta _{i}\), podrían resultar en\(\sin \theta _{t}\) ser mayores que la unidad. No hay ángulo real\(\theta _{t}\) que satisfaga esta condición. El ángulo crítico del incidente\(\theta _{c}\) se define como ese valor de lo\(\theta _{i}\) que hace\(\theta _{t}= \pi /2\),
\[ \sin \theta _{c}=c_{1}/c_{2} \nonumber \]
que tiene una solución real sólo si\(c_{1}<c_{2}\). En el ángulo crítico, el número de onda\(k_{zt}\) es cero. Los ángulos de incidencia menores tienen valores reales de\(k_{zt}\). Para ángulos de incidencia más grandes no hay ángulo real\(\theta _{t}\) que satisfaga (6). La ley de Snell siempre debe ser obedecida para satisfacer en absoluto\(z =0\) las condiciones limítrofes\(x\). Lo que sucede es que\(\theta _{t}\) se convierte en un número complejo que satisface (6). Aunque\(\sin \theta _{t}\) sigue siendo real,\(\cos \theta _{t}\) es imaginario cuando\(\sin \theta _{t}\) supera la unidad:
\[ \cos \theta _{t}=\sqrt{1-\sin ^{2}\theta _{t}} \nonumber \]
Esto hace entonces\(k_zt\) imaginario, que podemos escribir como
\[ k_{zt}=k_{2}\cos \theta _{t}=-j\alpha \nonumber \]
El signo negativo de la raíz cuadrada se toma para que las ondas ahora se descomponen con\(z\):
\ [\ begin {align}\ textbf {E} _ {t} &=\ textrm {Re}\ izquierda [\ hat {E} _ {t} e^ {j\ izquierda (\ omega t-k_ {xt} x\ derecha)} e^ {-\ alpha z}\ textbf {i} _ _ {y}\ derecha]\ nonumber\
\ textbf {H} _ {t} &=\ textrm {Re}\ izquierda [\ frac {\ sombrero {E} _ {t}} {\ eta_ {2}}\ izquierda (-\ cos\ theta _ {t}\ textbf {i} _ {x} +\ sin\ theta _ {t}\ textbf {i} _ {z}\ derecha ) e^ {j\ izquierda (\ omega t-k_ {xt} x\ derecha)} e^ {-\ alpha z}\ derecha]\ end {align}\ nonumber\]
Las soluciones son ahora ondas planas no uniformes, como se discute en la Sección 7-7.
Los ángulos complejos de transmisión son un concepto matemático válido. Lo que ha ocurrido es que en (1) escribimos nuestras supuestas soluciones para los campos transmitidos en términos de ondas puras de propagación. Las ecuaciones de Maxwell para un ángulo incidente mayor que el ángulo crítico requieren ondas espacialmente\(z\) en descomposición con región\(2\) para que las matemáticas forzaran\(k_zt\) a ser imaginarias.
No hay disipación de energía ya que el flujo\(z\) de potencia promedio en el tiempo dirigido es cero,
\[ \begin{align}<S_{z}>&= -\frac{1}{2}\textrm{Re}\left [ E_{y}H_{x}^{\ast }\right ]\nonumber \\ &= -\frac{1}{2}\textrm{Re}\left [ \frac{\hat{E}_{t}\hat{E}_{t}^{\ast }}{\eta_{2}}\left ( -\cos \theta _{t} \right )^{\ast }e^{-2\alpha z}\right ]=0\end{align} \nonumber \]
porque\(\cos \theta _{t}\) es puro imaginario para que el término entre corchetes en (21) sea puro imaginario. La potencia promedio\(z\) de tiempo dirigida por incidentes se refleja totalmente. A pesar de que la potencia\(z\) transmitida dirigida en promedio en el tiempo es cero, hay campos distintos de cero pero que se descomponen exponencialmente en la región\(2\).
\(H\)Campo Paralelo al Límite
Para esta polarización, ilustrada en la Figura 7-18b, los campos son
\ [\ begin {align}\ textbf {E} _ {i} &=\ textrm {Re}\ left [\ hat {E} _ {i}\ left (\ cos\ theta _ {i}\ textbf {i}\ textbf {i} _ {x} -\ sin\ theta _ {i}\ textbf {i} _ {z}\ derecha) e^ {j\ izquierda (\ omega t-k_ {xi} x-k_ {zi} z\ derecha)}\ derecha]\ nonumber
\\ textbf {H} _ {i} &=\ textrm {Re}\ izquierda [\ frac {\ sombrero {E} _ {i}} {\ eta_ {1}} e^ {j\ izquierda (\ omega t-k_ {xi} x-k_ {zi} z\ derecha)}\ textbf {i} _ {y}\ derecha]\ nonumber\
\ textbf {E} _ _ {r} &=\ textrm {Re}\ izquierda [\ hat {E} _ {r}\ izquierda (-\ cos\ theta _ {r}\ textbf {i} _ {x} -\ sin\ theta _ {r}\ textbf {i} _ _ {z}\ derecha) e^ {j\ izquierda (\ omega t-k_ {xr} x+k_ {zr} z\ derecha)}\ derecha]\ nonumber\
\ textbf {H} _ _ {r} &=\ textrm {Re}\ izquierda [\ frac {\ sombrero {E} _ {r}} {\ eta_ {1}} e^ {j\ izquierda (\ omega t-k_ {xr} x+k_ {zr} z\ derecha)}\ textbf {i} _ _ {y}\ derecha]
\ nonumber\
\ textbf {E} _ {t} &= textrm {Re}\ izquierda [\ hat {E} _ {t}\ izquierda (\ cos\ theta _ {t}\ textbf {i} _ _ {x} -\ sin\ theta _ {t}\ textbf {i} _ {z}\ derecha) e^ {j\ izquierda (\ omega t-k_ {xt } x-k_ {zt} z\ derecha)}\ derecha]\ nonumber\
\ textbf {H} _ {t} &=\ textrm {Re}\ izquierda [\ frac {\ hat {E} _ {t}} {\ eta_ {2}} e^ {j\ izquierda (\ omega t-k_ {xt} x-k_ {zt} z\ derecha)}\ textbf {i} _ {y}\ derecha]\ end {align}\ nonumber\]
donde los números de onda y las impedancias son los mismos que en (2) y (3).
Continuidad de tangencial\(\textbf{E}\) y\(\textbf{H}\) a\(z =0\) requiere
\ [\ hat {E} _ _ {i}\ cos\ theta _ {i} e^ {-jk_ {xi} x} -\ sombrero {E} _ _ {r}\ cos\ theta _ {r} e^ {-jk_ {xr} x} =\ sombrero {E} _ _ {t}\ cos\ theta _ {t} e^ {-jk_ {xt} x}\\
\ frac {\ sombrero {E} _ _ {i} e^ {-jk_ {xi} x} +\ sombrero {E} _ {r} e^ {-jk_ {xr} x}} {\ eta _ {1}} =\ frac {\ sombrero {E} _ _ {t} e^ {-jk_ {xt} x}} {\ eta _ {2}}\ nonumber\]
Nuevamente los factores de fase deben ser iguales para que (5) y (6) vuelvan a ser ciertos. La ley de Snell y el ángulo de incidencia que iguala el ángulo de reflexión son independientes de la polarización.
Resolvemos (23) para los coeficientes de reflexión y transmisión de campo como
\ [R=\ frac {\ sombrero {E} _ {r}} {\ sombrero {E} _ _ {i}} =\ frac {\ eta _ {1}\ cos\ theta _ {i} -\ eta _ {2}\ cos\ theta _ {t}} {\ eta _ {2}\ cos\ theta _ {t} + eta\ _ {1}\ cos\ theta _ {i}}\
T=\ frac {\ sombrero {E} _ {t}} {\ sombrero {E} _ {i}} =\ frac {2\ eta _ {2}\ cos\ theta _ {i}} {\ eta _ {2}\ cos\ theta _ {t} +\ eta _ {1}\ cos\ theta _ {i}}\ nonumber\]
Ahora observamos que la condición límite de continuidad de la normalidad\(\textbf{D}\) at\(z =0\) es redundante a la relación inferior en (23),
\[ \varepsilon_{1}\hat{E}_{1}\sin \theta _{i}+\varepsilon_{1}\hat{E}_{r}\sin \theta _{r}=\varepsilon_{2}\hat{E}_{t}\sin \theta _{t} \nonumber \]
usando la ley de Snell para relacionar los ángulos.
Para esta polarización la condición para que no haya ondas reflejadas es
\[ R=0\Rightarrow \eta _{2}\cos \theta _{t}=\eta _{1}\cos \theta _{i} \nonumber \]
que de la ley de Snell le da al ángulo Brewster:
\[ \sin ^{2}\theta_{B}=\frac{1-\varepsilon _{1}\mu _{2}/\left ( \varepsilon _{2}\mu _{1} \right )}{1-\left (\varepsilon _{1}/\varepsilon _{2} \right )^{2}} \nonumber \]
Ahora hay una solución para el caso habitual donde\(\mu _{1}=\mu _{2}\) pero\(\varepsilon _{1}\neq \varepsilon _{2}\):
\[ \sin ^{2}\theta _{B}=\frac{1}{1+\varepsilon_{1}/\varepsilon_{2}}\Rightarrow \tan \theta _{B}=\sqrt{\frac{\varepsilon_{2}}{\varepsilon_{1}}} \nonumber \]
En este ángulo de Brewster, los flujos de potencia reflejados y transmitidos están en ángulo recto\(\left ( \theta _{B}+\theta _{t}\right )=\pi /2 \) como se puede ver usando (6), (27) y (29)
\ [\ comenzar {alinear}\ cos\ izquierda (\ theta _ {B} +\ theta _ {t}\ derecha) &=\ cos\ theta _ {B}\ cos\ theta _ {t} -\ sin\ theta _ {B}\ sin\ theta _ {t}\ nonumber\\ &
=\ cos^ {2}\ theta _ {B}\ sqrt\ frac {\ varepsilon _ {2}} {\ varepsilon_ {1}}} -\ sin^ {2}\ theta _ {B}\ sqrt {\ frac {\ varepsilon_ {1}} {\ varepsilon_ {2}}}\ nonumber\\ &
=\ sqrt {\ frac {\ varepsilon_ {2}} {\ varepsilon_ {1}}} -\ sin^ {2}\ theta _ {B}\ izquierda (\ sqrt {\ frac {\ varepsilon_ {1}} {\ varepsilon _ {2}} +\ sqrt {\ frac {\ varepsilon_ {\ varepsilon _ {2}} +\ sqrt {\ frac {\ varepsilon_ psilon_ {2}} {\ varepsilon_ {1}}}\ derecha) =0
\ end {align}\ nonumber\]
Debido a que la ley de Snell es independiente de la polarización, el ángulo crítico de (17) es el mismo para ambas polarizaciones. Tenga en cuenta que el ángulo de Brewster para cualquier polarización, si existe, es siempre menor que el ángulo crítico de (17), como se puede ver particularmente cuando\(\mu _{1}=\mu _{2}\) para el campo magnético polarizado paralelo a la interfaz o cuando\(\varepsilon_{1}=\varepsilon_{2}\) para el campo eléctrico polarizado paralelo a la interfaz, como entonces
\[\frac{1}{\sin ^{2}\theta _{B}}=\frac{1}{\sin ^{2}\theta _{c}}+1 \nonumber \]


