9.4: Antenas dipolo largas

La potencia radiada, proporcional a\(\left ( dl/\lambda  \right )^{2}\), es pequeña para las antenas dipolo puntuales donde la longitud del dipolo\(dl\) es. mucho menor que la longitud de onda\(\lambda \). Se puede irradiar más potencia si se aumenta la longitud de la antena. Entonces, sin embargo, los campos debidos a cada sección de la antena pueden no agregar constructivamente.

Figura 9-9 Una matriz de dipolos de punto lineal con dipolos\(2N+1\) igualmente espaciados

Solución de campo lejano

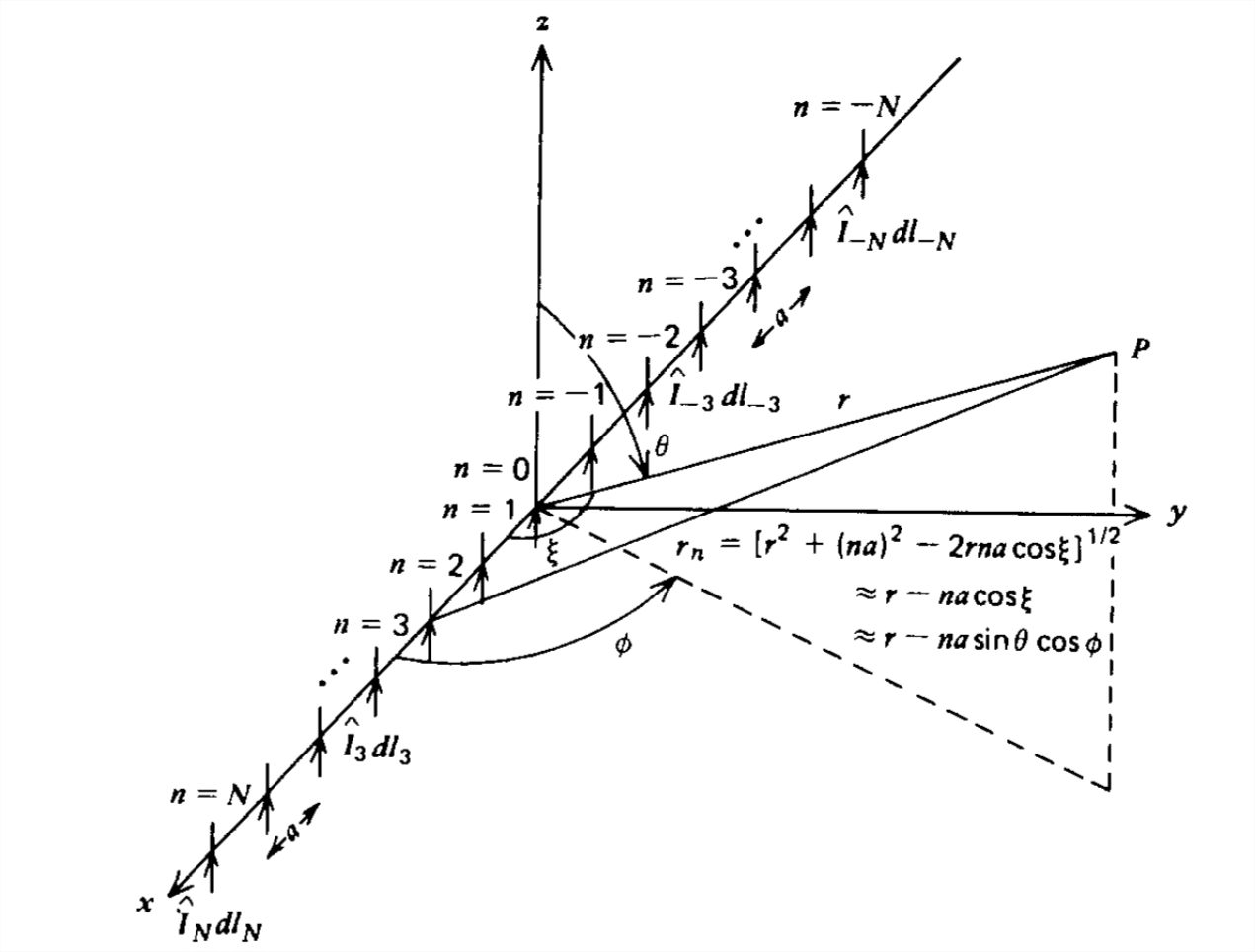
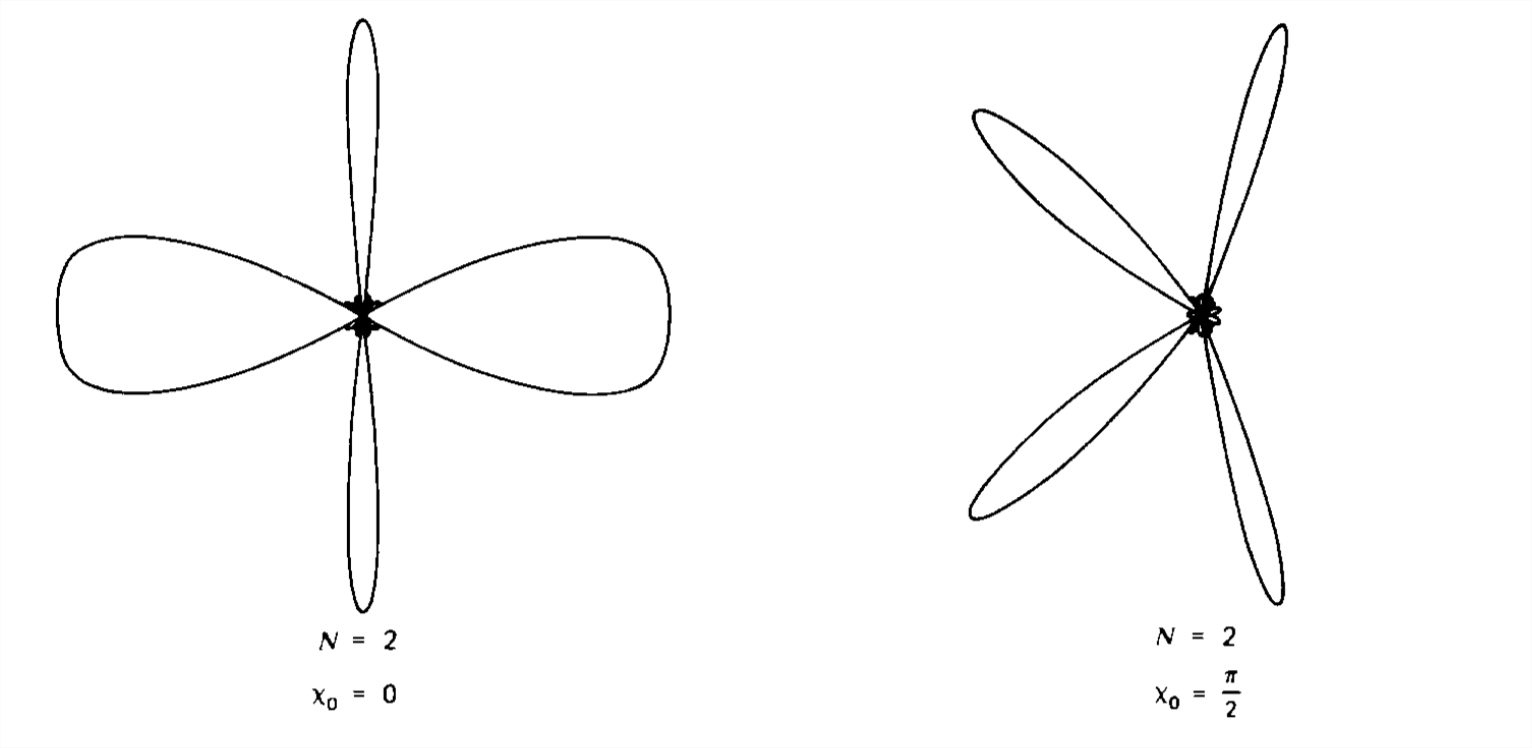
Considere la antena dipolo largo en la Figura 9-11 que transporta una corriente\(\hat{I}_{z}\). Por simplicidad nos limitamos al patrón de campo lejano donde\(r\gg L\). Entonces, como encontramos para las matrices de dipolos, las diferencias en la distancia radial para cada elemento de corriente incremental de longitud solo\(dz\) son importantes en los factores de fase exponenciales y no en las\(1/r\) dependencias.

De la Sección 9-2-3, el elemento de corriente incremental en la posición\(z\) genera un campo eléctrico lejano:

\[ d\hat{E}_{\theta }=\eta d\hat{H}_{\phi }=\frac{jk\eta }{4\pi }\frac{\hat{I}\left ( z \right )dz}{r}\sin \theta e^{-jk\left ( r-z\cos \theta  \right )} \nonumber \]

donde nuevamente asumimos que en el campo lejano el ángulo\(\) 6 es el mismo para todos los elementos de corriente incrementales.

El campo eléctrico lejano total debido a toda la distribución de corriente se obtiene por integración sobre todos los elementos de corriente:

\[ \hat{E}_{\theta }=\eta \hat{H}_{\phi }=\frac{jk\eta }{4\pi r}\sin \theta e^{-jkr}\int_{-L/2}^{+L/2}\hat{I}\left ( z \right )e^{jkz\cos \theta }dz \nonumber \]

Si se conoce la distribución de corriente, la integral en (2) puede evaluarse directamente. El problema práctico es difícil porque la distribución de corriente a lo largo de la antena está determinada por los campos cercanos a través de las condiciones de límite.

Figura 9-10 El patrón de radiación para una matriz lineal de\(N\) dipolos para diversos valores de\(N\)\(2a\), espaciado dipolar y fase de corriente relativa\(\mathcal{X}_0\) en el\(\theta =\pi /2\) plano.

Dado que los campos y las corrientes están acoplados, una solución exacta es imposible por simple que sea la geometría de la antena. En la práctica, se adivina una distribución actual y se calcula los campos resultantes (cercanos y lejanos). Si se satisfacen todas las condiciones de límite a lo largo de la antena, entonces se ha encontrado la solución. Desafortunadamente, esto nunca sucede con la primera conjetura. Así, con base en la solución de campo obtenida a partir de la corriente originalmente adivinada, se utiliza una distribución de corriente corregida y

Figura 9-10

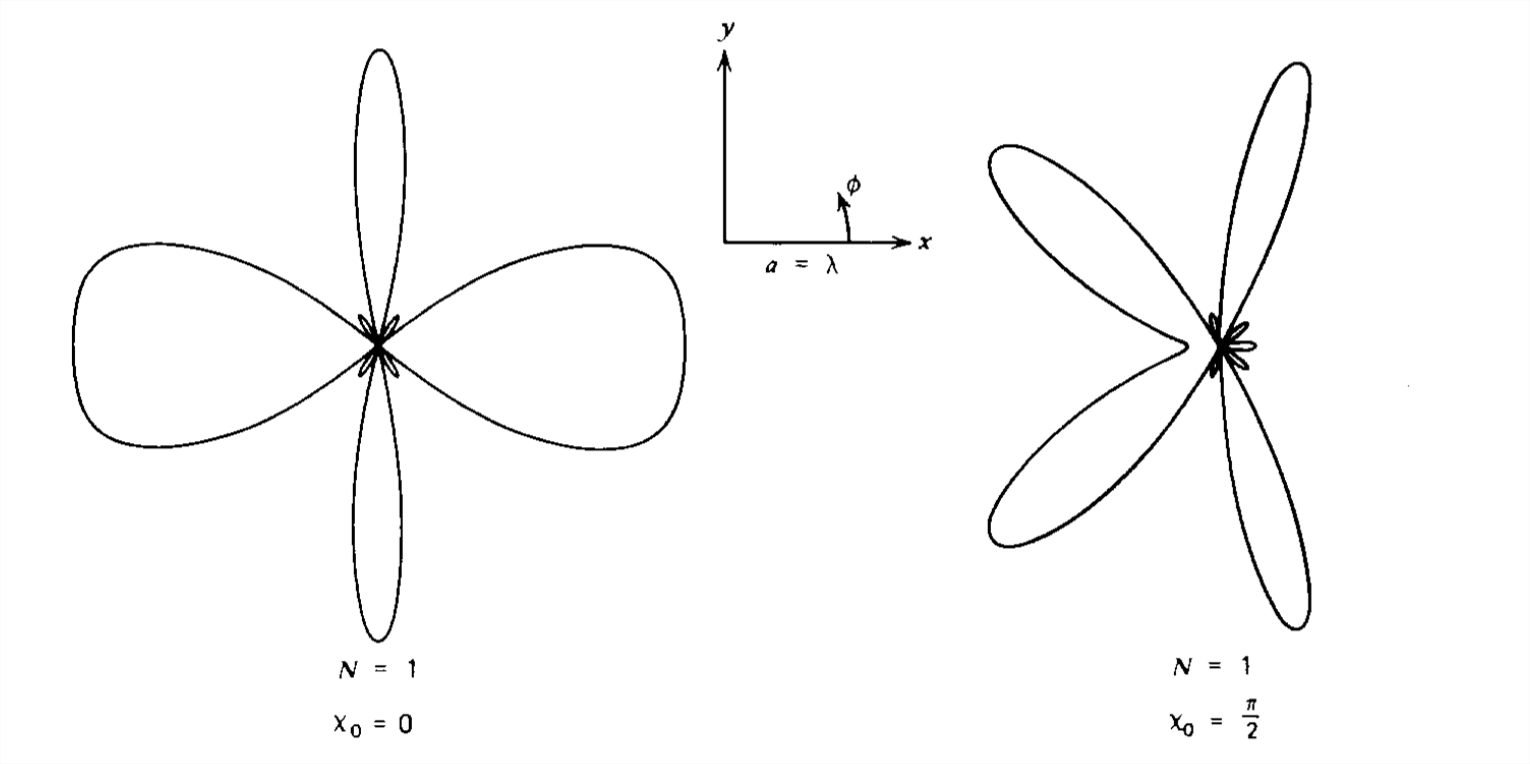
los campos resultantes se calculan de nuevo. Este procedimiento se repite numéricamente hasta que se obtiene la convergencia con campos y corrientes autoconsistentes.

Corriente Uniforme

Un caso particularmente sencillo es cuando\(\hat{I}_{z}=\hat{I}_{0}\) es una constante.

Entonces (2) se convierte en:

\ [\ begin {align}\ hat {E} _ {\ theta} =\ eta\ hat {H} _ {\ phi} &=\ frac {jk\ eta} {4\ pi r}\ sin\ theta e^ {-jkr}\ hat {I} _ {0}\ int_ {-L/2} ^ {+L/2} e^ {jkz\ cos\ theta} z\ nonumber\\ &
=\ frac {jk\ eta} {4\ pi r}\ sin\ theta e^ {-jkr}\ sombrero {I} _ {0}\ frac {e^ {jkz\ cos\ theta}} {jk\ cos}\ bigg|_ {-L/2} ^ {+L/2}\ nonumber\\ & ;
=\ frac {\ hat {I} _ {0}\ eta} {4\ pi r}\ tan\ theta e^ {-jkr}\ izquierda [2j\ sin\ izquierda (\ frac {kL} {2}\ cos\ theta\ derecha)\ end {align}\ nonumber\]

La densidad de potencia promedio en el tiempo es entonces

\[ <S_{r}>=\frac{1}{2\eta }\left | \hat{E}_{\theta } \right |^{2}=\frac{\left | \hat{E}_{0} \right |^{2}\tan ^{2}\theta \sin ^{2}\left [ \left ( kL/2 \right )\cos \theta  \right ]}{2\eta \left ( kr \right )^{2}\left ( kL/2 \right )^{2}} \nonumber \]

donde

\[ \hat{E}_{0}= \frac{\hat{I}_{0}L\eta k^{2}}{4\pi } \nonumber \]

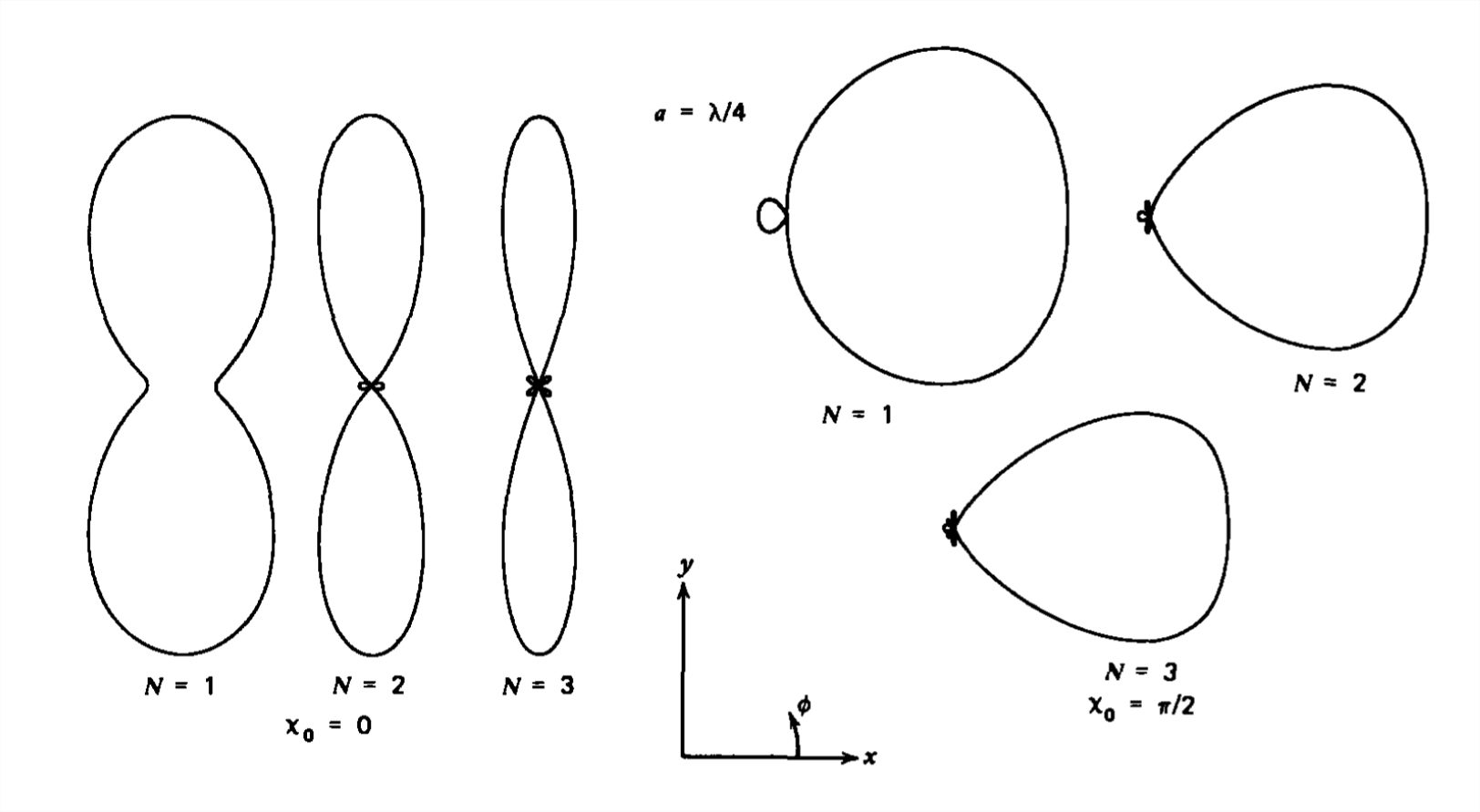
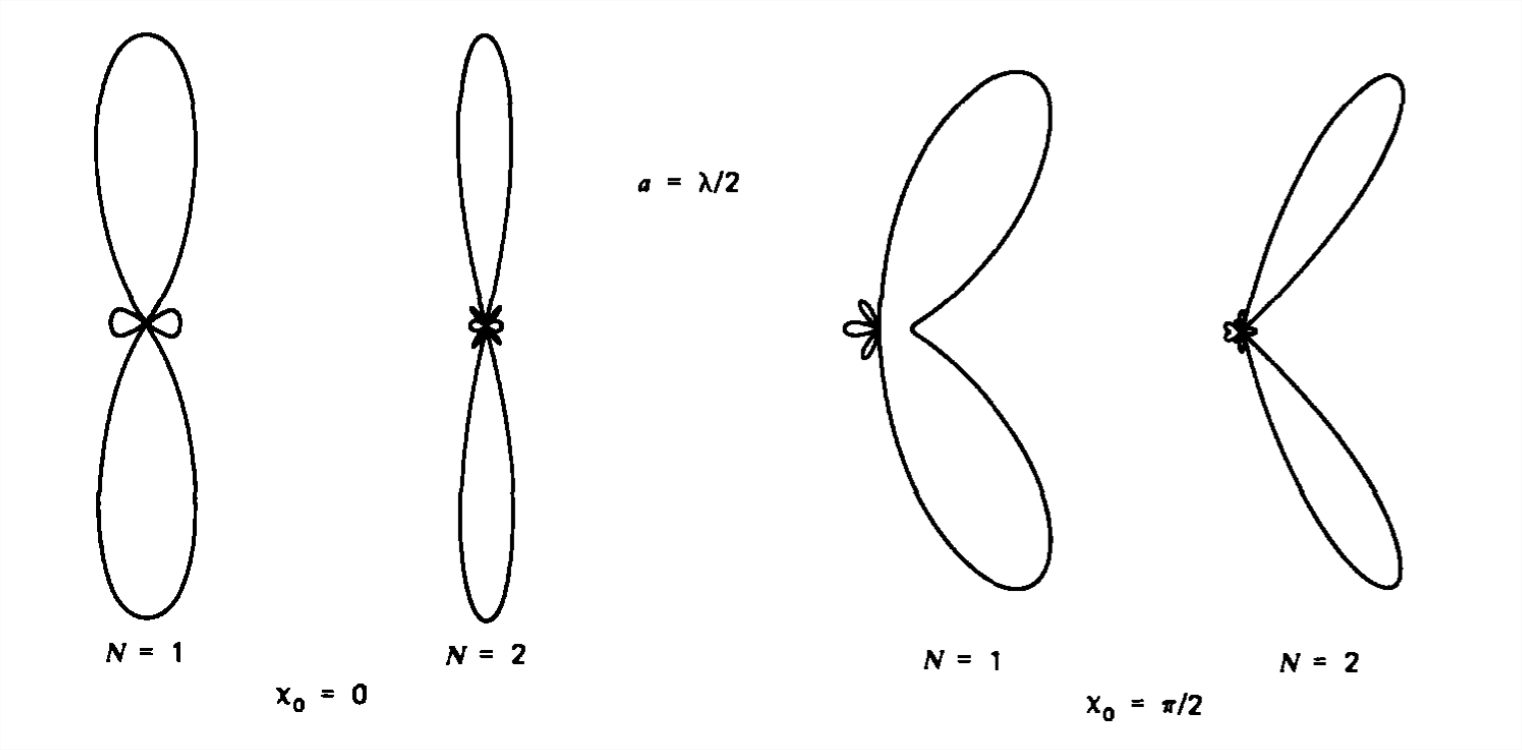
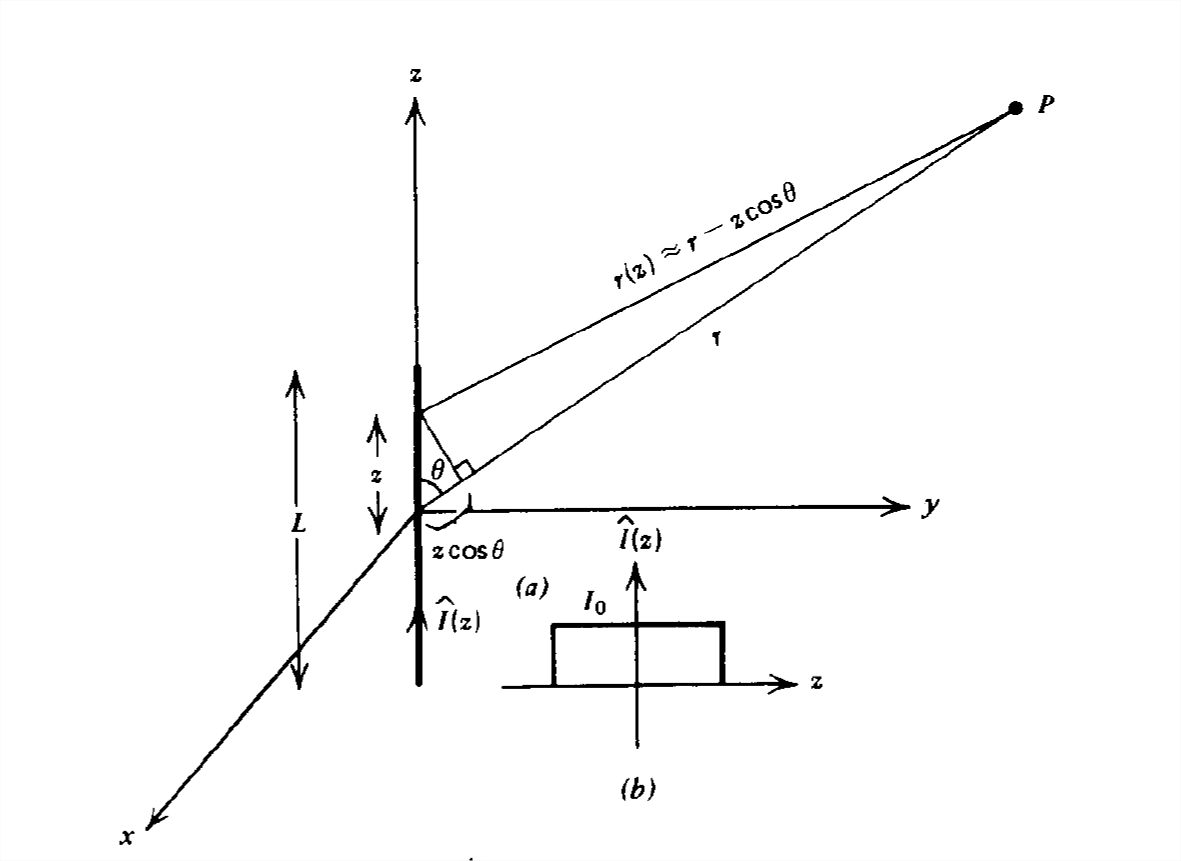
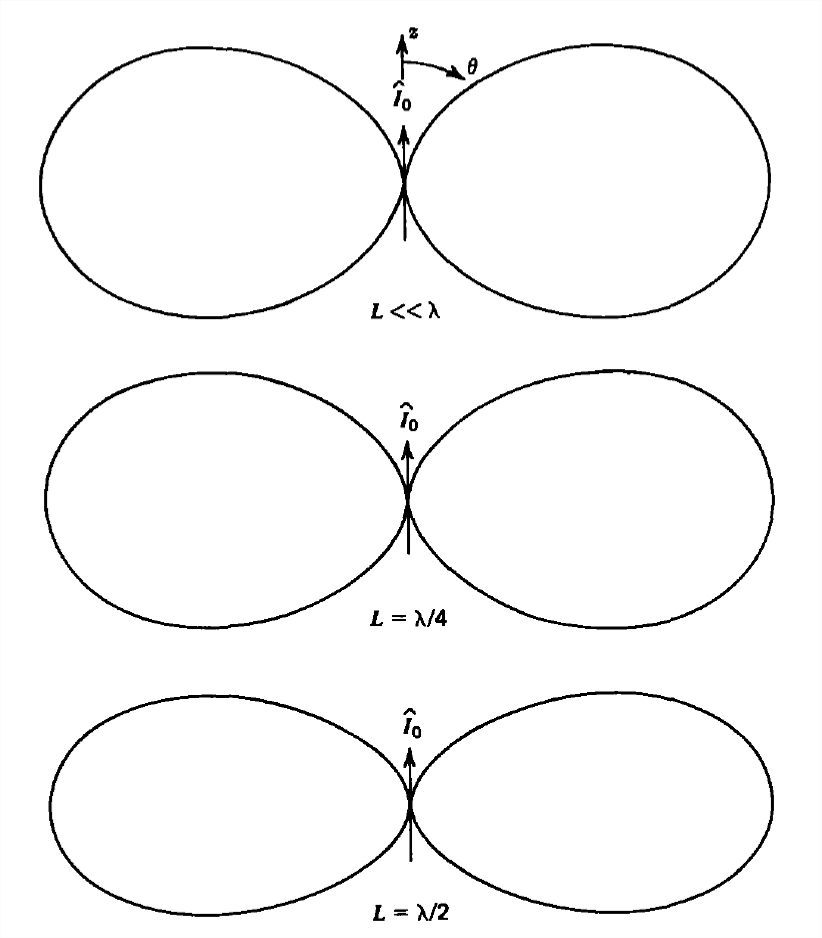
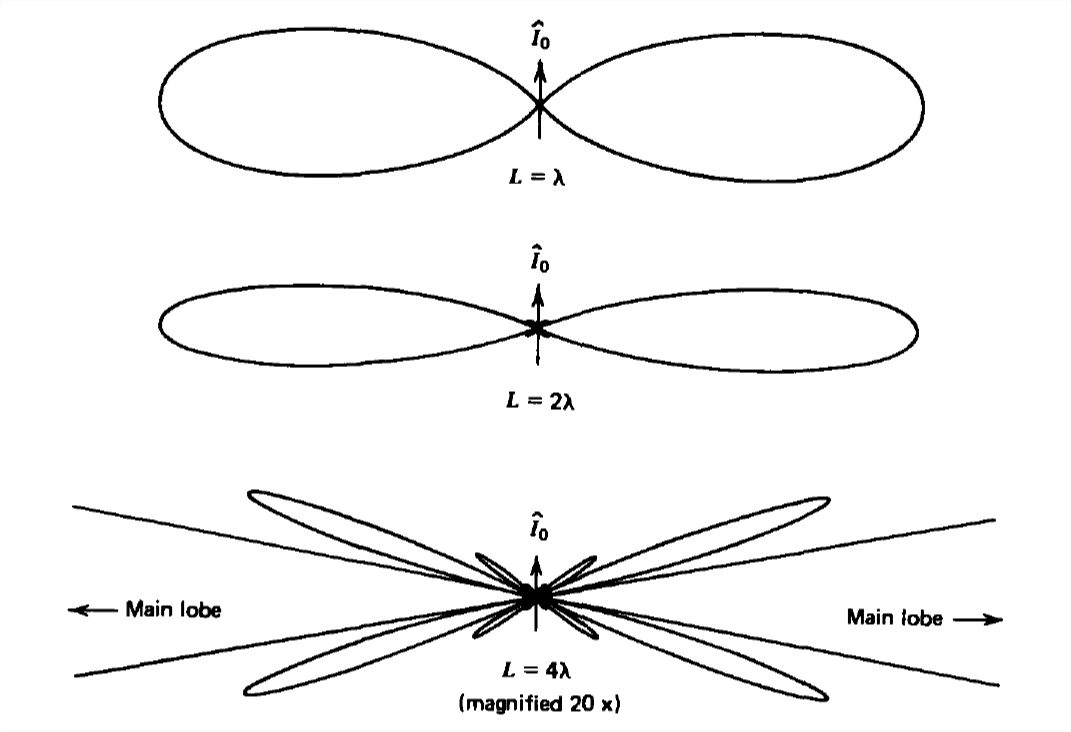
Esta densidad de potencia se representa en función del ángulo\(\theta \) en la Figura 9-12 para varias longitudes\(L\). El máximo principal siempre aparece en\(\theta =\pi /2\), volviéndose más agudo a medida que\(L\) aumenta. Para\(L >\lambda \), la densidad de potencia cero ocurre en ángulos

\[ \cos \theta =\frac{2n\pi }{kL}=\frac{n\lambda }{L},\quad n=1,2,... \nonumber \]

Los máximos secundarios ocurren luego en ángulos cercanos pero a amplitudes mucho más pequeñas en comparación con el lóbulo principal en\(\theta =\pi /2\).

Resistencia a la Radiación

La potencia radiada promedio en el tiempo total se obtiene integrando (4) en todos los ángulos:

\[ \begin{align} <P>&=\int_{\phi=0}^{2\pi }\int_{\theta =0}^{\pi }<S_{r}>r^{2}\sin \theta \,d\theta\, d\phi \nonumber \\ &=\frac{\left | \hat{E}_{0} \right |^{2}\pi }{k^{2}\eta \left ( kL/2 \right )^{2}}\int_{\theta =0}^{\pi }\frac{\sin ^{3}\theta }{\cos ^{2}\theta }\sin ^{2}\left ( \frac{kL}{2}\cos \theta \right )d\theta \end{align} \nonumber \]

Si introducimos el cambio de variable,

\[ v=\frac{kL}{2}\cos \theta ,\quad dv=-\frac{kL}{2}\sin \theta \,d\theta  \nonumber \]

la integral de (7) se convierte

\[ <P>=\frac{\left | \hat{E}_{0} \right |^{2}\pi }{k^{2}\eta \left ( kL/2 \right )^{2}}\int_{+kL/2}^{-kL/2}\left ( \frac{2}{kL}\sin ^{2}v\,dv-\frac{kL}{2}\frac{\sin ^{2}v}{v^{2}} \right )dv  \nonumber \]

El primer término es fácilmente integrable como

\[ \int \sin ^{2}v\,dv=\frac{1}{2}v-\frac{1}{4}\sin 2v \nonumber \]

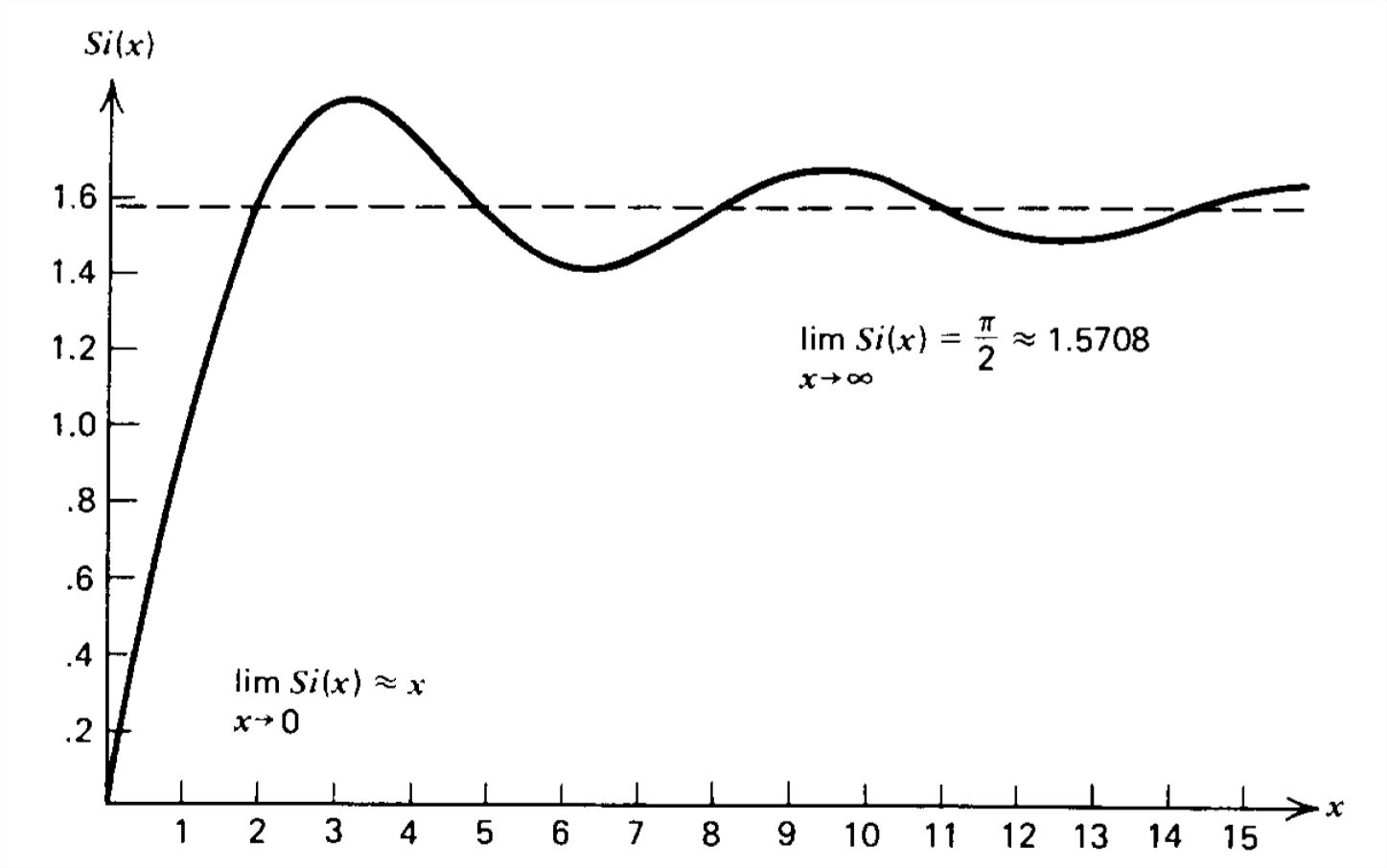
La segunda integral da como resultado una nueva función tabulada\(\) Si (x) llamada integral sinusoidal, definida como:

\[ Si\left ( x \right )=\int_{0}^{x}\frac{\sin t}{t}dt \nonumber \]

Figura 9-11 (a) Para una antena dipolo larga, cada elemento de corriente incremental en la coordenada\(z\) se encuentra a una distancia ligeramente diferente a cualquier punto de campo\(P\). b) El estudio de caso más simple tiene la corriente uniformemente distribuida sobre la longitud del dipolo.

que se representa en la Figura 9-13. Luego, la segunda integral en (9) se puede expandir e integrar por partes:

\ [\ begin {align}\ int\ frac {\ sin ^ {2} v} {v^ {2}} dv&=\ int\ frac {\ left (1-\ cos 2v\ derecha)} {2v^ {2}} dv\ nonumber\\ &
=-\ frac {1} {2v} -\ int\ cos 2v\ frac {dv} {2vv^ {2}}\ nonúmero\\ &
=-\ frac {1} {2v} +\ frac {\ cos 2v} {2v} +\ int\ frac {\ sin 2vd\ izquierda (2v\ derecha)} {2v}\ nonumber\\ &
=-\ frac {1} {2v} +\ frac {\ cos 2v} {2v} +Si\ izquierda (2v\ derecha)\ end {align}\ nonumber\]

Luego, al evaluar las integrales de (10) y (12) en (9) en los límites superior e inferior se obtiene la potencia promedio de tiempo como:

\[ <P>=\frac{\left | \hat{E}_{0} \right |^{2}\pi }{k^{2}\eta \left ( kL/2 \right )^{2}}\left ( \frac{\sin kL}{kL}+\cos kL-2+kLSi\left ( kL \right ) \right ) \nonumber \]

donde utilizamos el hecho de que la integral sinusoidal es una función impar\(Si\left (x\right )=-Si\left ( x\right )\).

Usando (5), la resistencia a la radiación es entonces

\[ R=\frac{2<P>}{\left | \hat{I}_{0} \right |^{2}}=\frac{\eta }{2\pi }\left ( \frac{\sin kL}{kL}+\cos kL-2+kLSi\left ( kL \right )\right ) \nonumber \]

Figura 9-12 El patrón de radiación para un dipolo largo para diversos valores de su longitud.

Figura 9-13 La integral sinusoidal\(Si(x)\) aumenta linealmente para argumentos pequeños y enfoques\(\pi /2\) para argumentos grandes oscilando sobre este valor para argumentos intermedios.

Figura 9-14 La resistencia a la radiación para una antena dipolo que porta una corriente uniformemente distribuida aumenta con el cuadrado de su longitud cuando es corta\(\left ( L/\lambda \ll 1 \right )\) y sólo linealmente con su longitud cuando es larga\(\left ( L/\lambda \gg  1 \right )\). Para longitudes cortas, la resistencia a la radiación se aproxima a la de un dipolo puntual.

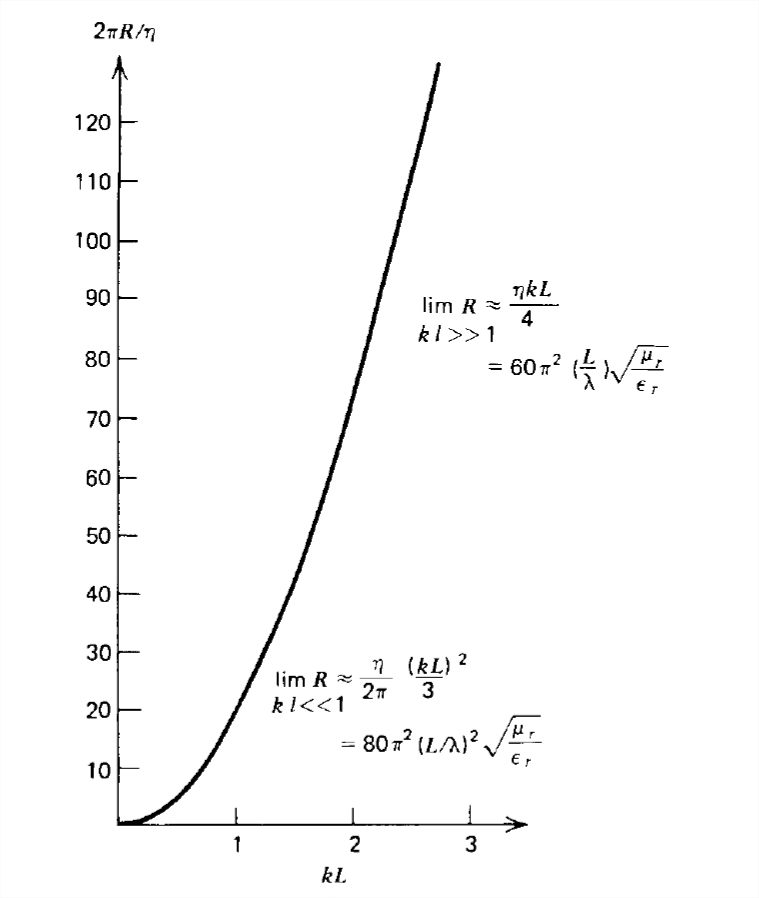
que se representa\(kL\) en comparación con la Fig. 9-14. Este resultado se puede verificar en el límite ya que\(L\) se vuelve muy pequeño\(\left ( kL\ll 1 \right )\) ya que la resistencia a la radiación debe acercarse a la de un dipolo puntual dado en la Sección 9-2-5. En este límite de dipolo corto los términos entre paréntesis en (14) son

\ [\ lim_ {kL\ ll 1}\ izquierda\ {\ begin {matriz}
\ displaystyle\ frac {\ sin kL} {kL}\ aprox 1-\ frac {\ izquierda (kL\ derecha) ^ {2}} {6}\\
\ displaystyle\ cos kL\ aprox 1-\ frac {\ izquierda (kL\ derecha) ^ {2}} {2} {kL
\\ displaystyle Si\ izquierda (kL\ derecha)\ aprox\ izquierda (kL\ derecha) ^ {2}
\ end {matriz}\ derecha. \ nonumber\]

de manera que (14) reduce a

\[ \lim_{kL\ll 1}R\approx \frac{\eta }{2\pi }\frac{\left ( kL \right )^{2}}{3}=\frac{2\pi \eta }{3}\left ( \frac{L}{\lambda } \right )^{2}=80\pi ^{2}\left ( \frac{L}{\lambda } \right )^{2}\sqrt{\frac{\mu _{r}}{\varepsilon _{r}}} \nonumber \]

que concuerda con los resultados de la Sección 9-2-5. Tenga en cuenta que para los dipolos grandes\(\left ( kL\gg 1 \right )\), el término integral sinusoidal domina con\(Si\left ( kL \right )\) acercarse a un valor constante de\(\pi /2\) tal manera que

\[ \lim_{kL\gg 1}R\approx \frac{\eta kL}{4}=60\sqrt{\frac{\mu _{r}}{\varepsilon _{r}}}\pi ^{2}\frac{L}{\lambda } \nonumber \]