4.9: Análisis de circuitos
- Page ID
- 82447
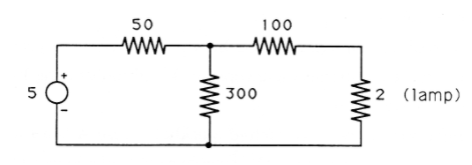
En esta sección utilizamos el álgebra lineal que hemos desarrollado para encontrar los voltajes y corrientes en un circuito eléctrico simple, como el que se muestra en la Figura 1. Hay muchas razones por las que esto podría ser necesario; en este ejemplo necesitamos conocer la corriente que fluye a través de la lámpara para decir si va a brillar o no. Muy poca corriente no tendrá ningún efecto visible; demasiada corriente hará que la lámpara se queme. Aplicaremos algunas leyes físicas que relacionan los voltajes y corrientes en un circuito, convertiremos estas leyes en sistemas de ecuaciones lineales, y resolveremos las ecuaciones para los voltajes y corrientes.
Corriente, voltaje y resistencia
Utilizaremos tres cantidades físicas en nuestro análisis de circuitos eléctricos: corriente, voltaje y resistencia. La corriente es el flujo de carga eléctrica de un lugar a otro. Los electrones que fluyen a través de un cable o a través de algún otro dispositivo electrónico comprenden una corriente. El voltaje es una diferencia en el potencial eléctrico que hace que los electrones fluyan. El voltaje a veces se llama fuerza electromotriz porque es como una “fuerza” que mueve electrones. La resistencia es una propiedad del dispositivo a través del cual fluye la corriente de electrones. Cuanto menor sea la resistencia de un dispositivo, más fácilmente la corriente puede fluir a través del dispositivo.
La analogía del agua que fluye a través de las tuberías puede ayudarte a desarrollar la intuición sobre los circuitos eléctricos. En esta analogía, la corriente eléctrica corresponde al caudal del agua. El voltaje corresponde a la presión que obliga al agua a fluir, y la resistencia es la fricción del flujo. Una tubería pequeña impediría el flujo de agua más que una tubería grande, por lo que la tubería pequeña correspondería a una mayor resistencia. Si bien esta analogía puede ser útil, hay que tener en cuenta que la electricidad no es agua. Todas las analogías se descomponen en algún momento.
Medimos la corriente eléctrica en amperios. El símbolo estándar para la corriente es\(i\), y la dirección del flujo positivo se indica con una flecha en el diagrama del circuito. La flecha es solo para referencia; si la corriente verdadera está en la dirección opuesta, obtenemos valores negativos para\(i\). Debido a que los electrones están cargados negativamente, la corriente se define como que fluye en la dirección opuesta al movimiento de los electrones. Pero para reducir la confusión, se debe aprender a pensar en términos de corriente más que movimiento de electrones.
Un punto en un circuito donde varios dispositivos están conectados entre sí se llama nodo. La ley de conservación para corriente dice que “lo que fluye adentro debe fluir fuera de un nodo”, principio conocido como ley vigente de Kirchhoff. La ley actual de Kirchhoff establece que la suma de todas las corrientes que salen de un nodo es cero. En esta ley, una corriente que ingresa al nodo se considera una corriente negativa que sale del nodo.
El voltaje se mide en voltios y generalmente se escribe como\(\nu\) (o\(e\)). Dado que el voltaje es una diferencia de potencial entre dos puntos (nodos), podemos mostrarlo en un diagrama de circuito con un signo + y un signo —para indicar qué dos nodos estamos comparando y cuál de los nodos se considera negativo. Al igual que con la corriente, las marcas son solo para referencia y podemos terminar con un valor negativo de\(\nu\).
En un circuito eléctrico, generalmente se elige un nodo como nodo de referencia y se considera que tiene una tensión de cero. Entonces se mide el voltaje en cada otro nodo con respecto al nodo de referencia. Esto nos ahorra la molestia de especificar siempre pares de nodos para mediciones de voltaje y marcar señales + y — para cada voltaje. Otros nombres para el nodo de referencia son comunes y terrestres.
Una fuente de voltaje constante es un dispositivo que siempre obliga a que el voltaje entre sus dos terminales sea un valor constante. En la Figura 1 el círculo de la izquierda representa una fuente de voltaje constante de 5 voltios, de manera que el voltaje en el extremo superior (+) es siempre exactamente 5 voltios más alto que el voltaje en el extremo inferior (-). Una fuente de voltaje es algo así como una batería, pero idealizada. Las baterías reales no mantienen un voltaje de salida constante bajo todas las condiciones.
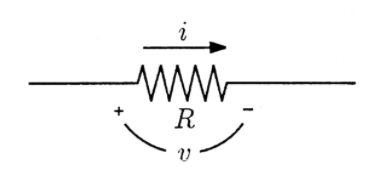
La resistencia se mide en ohmios y se denota por\(R\). Una resistencia se muestra como una línea en zig-zag en diagramas de circuito y etiquetada con el valor de su resistencia en ohmios. En este capítulo consideraremos únicamente dispositivos cuya resistencia sea positiva y la misma en ambos sentidos. La ley de Ohm, también llamada ley de resistencias, relaciona el voltaje y la corriente en una resistencia. Para la resistencia mostrada en la Figura 2, con direcciones de referencia asignadas\(\nu\) y\(i\) como se muestra, la ley de Ohm es
\[\nu=i R \nonumber \]
Tenga en cuenta que la corriente fluye de + a - a través de la resistencia.
La ley de Ohm y la ley actual de Kirchhoff son los únicos principios que necesitamos para escribir ecuaciones que nos permitan encontrar los voltajes y corrientes en el circuito resistivo de la Figura 1. Comenzamos eligiendo un nodo de referencia y asignando variables a los voltajes en cada otro nodo (con respecto al nodo de referencia). Estas opciones se muestran en la Figura 3.
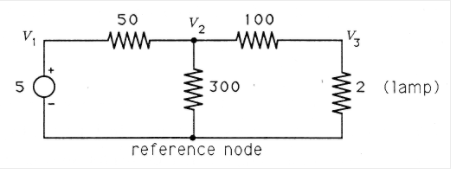
La fuente de voltaje constante obliga\(\nu _1\) a ser exactamente 5 voltios más alta que el nodo de referencia. Por lo tanto
\[\nu _{1}=5 \nonumber \]
A continuación escribimos ecuaciones aplicando la ley actual de Kirchhoff a cada nodo del circuito (excepto el nodo de referencia y\(\nu _1\), cuyos voltajes ya conocemos). En el nodo etiquetado\(\nu _2\) hay tres rutas para dejar actual. La corriente que sale a través de la resistencia de 50 ohmios se puede encontrar según la ley de Ohm, donde el voltaje a través de esa resistencia es\(\nu _2 − \nu _1\):
\[i_{50}=\frac{v}{R}=\frac{\left(v_{2}-v_{1}\right)}{50} \nonumber \]
Para la corriente que sale a través de la resistencia de 300 ohmios, el voltaje es\(\nu _2\). Preste mucha atención al letrero; ya que nos interesa que la corriente salga del nodo etiquetado\(\nu _2\), la Figura 4.14 indica que para aplicar la ley de Ohm debemos tomar el voltaje como\(+ \nu _2 −\) referencia =\(\nu _2 − 0 = \nu _2\). Entonces
\[i_{300}=\frac{v_{2}}{300} \nonumber \]
Para la resistencia de 100 ohmios, podemos escribir
\[i_{100}=\frac{\left(v_{2}-v_{3}\right)}{100} \nonumber \]
Según la ley vigente de Kirchhoff, la suma de estas tres corrientes de salida es cero:
\ [\ begin {align}
\ quad\ tfrac {\ left (v_ {2} -v_ {1}\ derecha)} {50} +\ tfrac {v_ {2}} {300} +\ tfrac {\ izquierda (v_ {2} -v_ {3}\ derecha)} {100} =0\ nonumber\
\ fila derecha 6\ izquierda (v_ _ {2} -v_ {1}\ derecha) +v_ {2} +3\ izquierda (v_ {2} -v_ {3}\ derecha) =0\ nonumber\\
\ Rightarrow\ qquad\ quad -6 v_ {1} +10 v_ {2} -3 v_ {3} =0 \ label {}
\ end {align}\ nonumber\]
Observe que cuando escribimos la ecuación para el nodo etiquetado\(\nu _2\), la variable\(\nu _2\) tenía un signo + cada vez que ocurría en la ecuación, mientras que las demás tenían un signo -. Este es siempre el caso, y estar atento a ello puede ayudarte a evitar errores en las señales. Ahora aplicamos la ley actual de Kirchhoff en el nodo etiquetado\(\nu _3\) para obtener la ecuación
\ [\ begin {align}
\ frac {\ left (v_ {3} -v_ {2}\ derecha)} {100} +\ frac {v_ {3}} {2} =0\ nonumber\
\ Rightarrow\ quad\ izquierda (v_ {3} -v_ {2}\ derecha) +50 v_ {3} =0\ nonumber\
\ Derecha tarrow\ quad 0 v_ {1} -1 v_ {2} +51 v_ {3} =0\ label {}
\ end {align}\ nonumber\]
Tenga en cuenta que esta vez es la\(\nu _3\) que siempre aparece con un signo +.
Las ecuaciones 2, 6 y 7 nos dan un sistema de tres ecuaciones en las tres variables desconocidas\(\nu _1\),\(\nu _2\), y\(\nu _3\). Ahora los escribimos en forma de matriz como
\ [\ left [\ begin {array} {lll}
1 & 0 & 0\\
-6 & 10 & -3\\
0 & -1 & 51
\ end {array}\ right]\ left [\ begin {array} {l}
v_ {1}\\
v_ {2}\\
v_ {3}
\ end {array}\ right] =\ left [\ begin {array } {l}
5\\
0\
0
\ end {array}\ derecha]\ nonumber\]
(MATLAB) Utilice MATLAB para resolver la Ecuación 8. Deberías encontrar
\(\nu _1\)= 5.0000 voltios
\(\nu _2\)= 3.0178 voltios
\(\nu _3\)= 0.0592 voltio
¿Cuál es el determinante de la matriz de coeficientes\(A\)? ¿La solución es única?
Podemos determinar la corriente que fluye a través de la lámpara desde\(\nu _3\) a tierra en el Ejemplo 1 por la ley de Ohm:
\[i=\frac{\nu}{R}=\frac{\nu _{3}}{2}=0.0296 \text { ampere } \nonumber \]
El efecto visible dependerá, por supuesto, de la lámpara. Supongamos que las especificaciones de nuestra lámpara indican que se requiere 0.05 amperios o más antes de que brille, y más de 0.075 amperios hará que se queme. En este caso, nuestro circuito no haría brillar la lámpara.
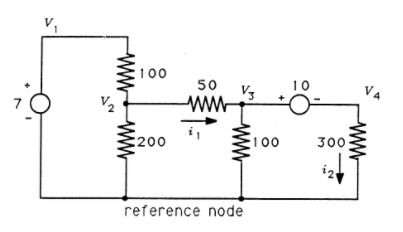
(MATLAB) Escribe y resuelve ecuaciones para el circuito en la Figura 4. ¿Cuáles son los voltajes en los nodos etiquetados\(\nu _1\) a través\(\nu _4\)? ¿Cuál es la etiqueta actual\(i_1\)? \(i_2\)¿Y?