5.1: Introducción a los gráficos vectoriales
- Page ID
- 82348
Agradecimientos
Fundamentos de los gráficos interactivos por computadora de J. D. Foley y A. Van Dam, ©1982 Addison-Wesley Publishing Company, Inc., Reading, Massachusetts, se utilizó ampliamente como libro de referencia durante el desarrollo de este capítulo. Las ubicaciones estelares se obtuvieron del programa de compartición “Deep Space” de David Chandler, quien las obtuvo de la base de datos “Skymap” del Centro Nacional de Datos de Ciencias Espaciales.
Apuntes a Profesores y Alumnos:
En este capítulo presentamos estructuras de datos matriciales que pueden ser utilizadas para representar imágenes bidimensionales y tridimensionales. El programa de demostración muestra a los estudiantes cómo crear un archivo de función para crear imágenes a partir de estas estructuras de datos. Luego mostramos cómo usar transformaciones matriciales para traducir, escalar y rotar imágenes. Las proyecciones se utilizan para proyectar imágenes tridimensionales en planos bidimensionales colocados en ubicaciones arbitrarias. Son precisamente tales proyecciones las que utilizamos para obtener dibujos en perspectiva sobre una superficie bidimensional de objetos tridimensionales. El experimento numérico anima a los estudiantes a manipular un campo estelar y verlo desde varios puntos del espacio.
Una vez más consideramos ciertos problemas esenciales para el desarrollo del capítulo. Para este capítulo asegúrate de no perderte los siguientes ejercicios: Ejercicio 2 en “Transformaciones de Imagen Bidimensional”, Ejercicio 1 en “Coordenadas Homogéneas”, Ejercicio 2 en “Coordenadas Homogéneas”, Ejercicio 5 en “Coordenadas Homogéneas Tridimensionales”, y Ejercicio 2 en “Proyecciones”.
Introducción
Las imágenes juegan un papel vital en la comunicación humana, en la fabricación robótica y en la imagen digital. En una aplicación típica de imágenes digitales, una cámara CCD graba un marco de imagen digital que se lee en la memoria de una computadora digital. La computadora digital luego manipula este marco (o matriz) de datos con el fin de recortar, agrandar o reducir, mejorar o suavizar, traducir rotar la imagen original. Estos procedimientos se denominan procesamiento digital de imágenes o gráficos por computadora. Cuando se procesa una secuencia de fotogramas y se muestra a velocidades de fotogramas de video (30 fotogramas por segundo), entonces tenemos una imagen animada.
En este capítulo utilizamos el álgebra lineal que desarrollamos en El capítulo sobre Álgebra Lineal para desarrollar un rudimentario conjunto de herramientas para hacer gráficos por computadora en dibujos lineales. Comenzamos con un ejemplo: la rotación de un solo punto en el\((x,y)\) plano.
\(P\)El punto tiene coordenadas (3,1) en el\((x,y)\) plano como se muestra en la Figura 1. Encuentra las coordenadas del punto\(P'\), desde el cual se gira\(\frac{\pi}{6}\) radianes\(P\).
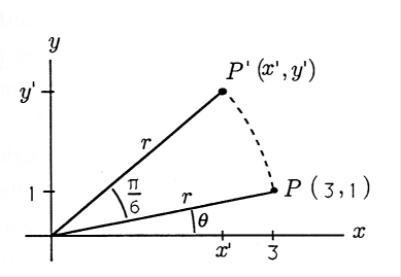
Para resolver este problema, podemos comenzar convirtiendo el punto\(P\) de coordenadas rectangulares a coordenadas polares. Tenemos
\[r=\sqrt{x^{2}+y^{2}}=\sqrt{10} \nonumber \]
\[\theta=\tan ^{-1}\left(\frac{y}{x}\right) \approx 0.3217 \nonumber \]radián.
El punto girado\(P'\) tiene el mismo radio\(r\), y su ángulo es\(\theta + \frac{\pi}{6}\). Ahora convertimos de nuevo a coordenadas rectangulares para encontrar\(x'\) y\(y'\) para punto\(P'\):
\[x^{\prime}=r \cos \left(\theta+\frac{\pi}{6}\right) \approx \sqrt{10} \cos (0.8453) \approx 2.10 \nonumber \]
\[y^{\prime}=r \sin \left(\theta+\frac{\pi}{6}\right) \approx \sqrt{10} \sin (0.8453) \approx 2.37 \text { . } \nonumber \]
Entonces el punto girado\(P'\) tiene coordenadas (2.10, 2.37).
Ahora imagínese tratando de rotar la imagen gráfica de algún objeto complejo como un avión. Podrías intentar rotar todos los 10,000 (más o menos) puntos de la misma manera que el punto único se acaba de rotar. Sin embargo, una forma mucho más fácil de rotar todos los puntos juntos es proporcionada por el álgebra lineal. De hecho, con una sola operación algebraica lineal podemos rotar y escalar un objeto completo y proyectarlo de tres dimensiones a dos para su visualización en una pantalla plana u hoja de papel.
En este capítulo estudiamos los gráficos vectoriales, un método algebraico lineal de almacenamiento y manipulación de imágenes informáticas. Los gráficos vectoriales son especialmente adecuados para mover, rotar y escalar (ampliar y reducir) imágenes y objetos dentro de las imágenes. El recorte también suele ser necesario, aunque es un poco más difícil con los gráficos vectoriales. Los gráficos vectoriales también nos permiten almacenar objetos en tres dimensiones y luego ver los objetos desde varias ubicaciones en el espacio mediante proyecciones.
En los gráficos vectoriales, las imágenes se dibujan a partir de líneas rectas. 1 Una curva puede aproximarse tan cerca como se desee mediante una serie de líneas cortas y rectas. Claramente algunas imágenes son más adecuadas para la representación por líneas rectas que otras. Por ejemplo, podemos lograr una representación bastante buena de un edificio o un avión en gráficos vectoriales, mientras que una fotografía de un bosque sería extremadamente difícil de convertir a líneas rectas. Muchos programas de diseño asistido por computadora (CAD) utilizan gráficos vectoriales para manipular dibujos mecánicos.
Cuando llega el momento de mostrar realmente una imagen de gráficos vectoriales, puede ser necesario alterar la representación para que coincida con el dispositivo de visualización. Las pantallas de visualización de computadoras personales se dividen en miles de pequeños rectángulos llamados elementos de imagen, o píxeles. Cada píxel está apagado (negro) o encendido (quizás con intensidad y/o color variables). Con una pantalla CRT, el haz de electrones escanea las filas de píxeles en un patrón ráster. Para dibujar una línea en un dispositivo de visualización de píxeles, primero debemos convertir la línea en una lista de píxeles para ser iluminados. Las impresoras matriciales y láser también son dispositivos de visualización de píxeles, mientras que los plotters de lápiz y algunos dispositivos CRT especializados pueden mostrar gráficos vectoriales directamente. Dejaremos que MATLAB haga la conversión a píxeles y maneje automáticamente el recorte cuando sea necesario.
Comenzamos nuestro estudio de los gráficos vectoriales representando cada punto en una imagen por un vector. Estos vectores están dispuestos uno al lado del otro en una matriz\(G\) que contiene todos los puntos de la imagen. Otras matrices serán utilizadas como operadores para realizar las transformaciones deseadas en los puntos de imagen. Por ejemplo, encontraremos una matriz\(R\), que funciona como rotación: el producto matriz\(RG\) representa una versión rotada de la imagen original\(G\).
Notas al pie
- Es posible extender estas técnicas para hacer frente a algunos tipos de curvas, pero consideraremos solo líneas rectas en aras de la simplicidad.