5.2: Representación de imagen bidimensional
- Page ID
- 82349
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Matriz de puntos
Para representar una imagen de línea recta en la memoria de la computadora, debemos almacenar una lista de todos los extremos de los segmentos de línea que componen la imagen. Si el punto\(P_i=(x_i,y_i)\) es tal punto final, lo escribimos como el vector de columna
\ [\ mathrm {p} _ {i} =\ left [\ begin {array} {l}
x_ {i}\\
y_ {i}
\ end {array}\ derecha]\ nonumber\]
Supongamos que hay\(n\) tales puntos finales en toda la imagen. Cada punto se incluye solo una vez, aunque varias líneas terminen en el mismo punto. Podemos organizar los vectores\(P_i\) en una matriz de puntos:
\ [\ begin {align}
\ mathrm {G} &=\ left [\ mathrm {p} _ {1}\ mathrm {p} _ {2}\ mathrm {p} _ {3}\ ldots\ mathrm {p} _ {n}\ derecha]\ nonumber\\
&=\ left [\ begin {array} {llll}
x_ {1} & x_ {2} & x_ {3} & x_ {n}\\
y_ {1} & y_ {2} & y_ {3} & y_ {n}
\ end {array}\ right].
\ end {align}\ nonumber\]
Luego almacenamos la matriz de puntos\(\mathrm{G} \in \mathscr{R}^{2 \mathrm{x} n}\) como una matriz bidimensional en la memoria de la computadora.
Considera la lista de puntos
\ (\ comenzar {reunido}
P_ {1} =( 0,0)\\
P_ {2} =( -1.5,5)\\
P_ {3} =( 4,2.3)\\
P_ {4} =( 4, -1)
\ final {reunido}\)
La matriz de puntos correspondiente es
\ [G=\ left [\ begin {array} {llll}
0 & -1.5 & 4 & 4\\
0 & 5 & 2.3 & -1
\ end {array}\ right]\ nonumber\]
Matriz de Línea
Lo siguiente que necesitamos saber es qué pares de puntos conectar con líneas. Para almacenar esta información para\(m\) líneas, utilizaremos una matriz de líneas,\(\mathrm{H} \in \mathscr{R}^{2 \times m}\). La matriz de líneas no almacena las ubicaciones de las líneas directamente. Más bien, contiene referencias a los puntos almacenados en\(G\). Para indicar una línea entre puntos\(p_i\) y\(p_j\), almacenamos los índices\(i\) y\(j\) como par. Para la\(k^{th}\) línea en la imagen, tenemos el par
\ [\ mathrm {h} _ {k} =\ left [\ begin {array} {c}
i_ {k}\\
j_ {k}
\ end {array}\ derecha]\ nonumber\]
El orden de\(i\) y realmente\(j\) no importa ya que una línea de\(p_i\) a\(p_j\) es lo mismo que una línea de\(p_j\) a\(p_i\). A continuación recogemos todas las líneas\(h_k\) en una matriz de líneas\(H\):
\ [\ mathrm {H} =\ left [\ begin {array} {lllll}
i_ {1} & i_ {2} & i_ {3} &\ ldots & i_ {m}\\
j_ {1} & j_ {2} & j_ {3} &\ ldots & j_ {m}
\ end {array}\ derecha]. \ nonumber\]
Todos los números en la matriz de líneas\(H\) serán enteros positivos ya que apuntan a columnas de\(G\). Para encontrar los extremos reales de una línea, observamos las columnas\(i\) y\(j\) de la matriz de puntos\(G\).
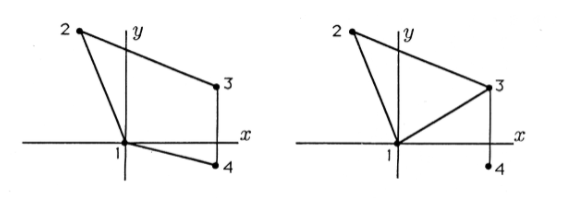
Para especificar segmentos de línea que conectan los cuatro puntos del Ejemplo 1 en un cuadrilátero, usamos la matriz de líneas
\ [\ mathrm {H} _ {1} =\ left [\ begin {array} {llll}
1 & 2 & 3 & 4\\
2 & 3 & 4 & 1
\ end {array}\ derecha]\ nonumber\]
Alternativamente, podemos especificar segmentos de línea para formar un triángulo desde los tres primeros puntos más una línea de\(P_3\) a\(P_4\):
\ [\ mathrm {H} _ {2} =\ left [\ begin {array} {llll}
1 & 2 & 3 & 3\\
2 & 3 & 1 & 4
\ end {array}\ right]. \ nonumber\]
En la Figura 1 se muestran los puntos\(G\) conectados primero por\(H_1\) y luego por\(H_2\).
Demostración 1 (MATLAB)
Utilice su editor para ingresar el siguiente archivo de función MATLAB. Guárdalo como vgraphl.m.
function vgraphl (points, lines);
% vgraphl (points, lines) plots the points as *'s and
% connects the points with specified lines. The points
% matrix should be 2xN, and the lines matrix should be 2xM.
% The field of view is preset to (-50,50) on both axes.
%
% Written by Richard T. Behrens, October 1989
%
m=length(lines); % find the number of
% lines.
axis([-50 50 -50 50]) % set the axis scales
axis('square')
plot(points(1,:),points(2,:),'*') % plot the points as *
hold on % keep the points...
for i=i:m % while plotting the
% lines
plot([points(1,lines(1,i)) points(1,lines(2,i))],..
[points(2,lines(2,lines(1,i)) points(2,lines(2,i))],'-')
end
hold off
Después de haber guardado el archivo de función, ejecute MATLAB y escriba lo siguiente para ingresar las matrices de punto y línea. (Comenzamos con las transposiciones de las matrices para que sean más fáciles de ingresar).
>> G = [
0.6052 -0.4728;
-0.4366 3.5555;
-2.6644 7.9629;
-7.2541 10.7547;
-12.5091 11.5633;
-12.5895 15.1372;
-6.5602 13.7536;
-31.2815 -7.7994;
-38.8314 -9.9874;
-44.0593 -1.1537;
-38.8314 2.5453;
-39.4017 9.4594;
-39.3192 15.0932;
-45.9561 23.4158]
>> G = G'
>> H = [
1 2;
2 3;
3 4;
4 5;
4 7;
5 6;
8 9;
9 10;
10 11;
11 12;
12 13;
12 14]
>> H = H'
En este punto deberías usar el comando “save” de MATLAB para guardar estas matrices en un archivo de disco. Tipo
>> save dippers
Después de haber guardado las matrices, utilice la función VGRAPH1 para dibujar la imagen escribiendo
>> vgraph1(G,H)
La ventaja de almacenar puntos y líneas por separado es que un objeto se puede mover y escalar operando solo en la matriz de puntos\(G\). La información de línea en\(H\) sigue siendo la misma ya que los mismos pares de puntos están conectados sin importar dónde pongamos los puntos ellos mismos.
Superficies y Objetos. Describir una superficie en tres dimensiones es una tarea bastante compleja, especialmente si la superficie es curva. Por esta razón, estaremos satisfechos con puntos y líneas, a veces visualizando superficies planas basadas en las líneas. Por otro lado, es una cuestión bastante simple agrupar los puntos y líneas en distintos objetos. Podemos definir una matriz de objeto\(K\) con una columna para cada objeto dando los rangos de puntos y líneas asociadas a ese objeto. Cada columna se define como
\ [\ mathrm {k} _ {i} =\ left [\ begin {array} {cc}
\ texto {primero} &\ texto {punto}\
\ texto {último} &\ texto {último} &\ texto {punto}
\\\ texto {primero} &\ texto {línea}
\\ texto {último} &\ texto {línea}
\ final {array}\ derecho]\ nonumber\]
Al igual que con la matriz de líneas\(H\), los elementos de\(K\) son enteros.
Considerar de nuevo Demo 1. Podríamos agrupar los puntos en\(G\) y las líneas\(H\) en dos objetos con la matriz
\ [K=\ left [\ begin {array} {ll}
1 & 8\\
7 & 14\\
1 & 7\\
6 & 12
\ end {array}\ derecha]\ nonumber\]
La primera columna de\(K\) especifica que el primer objeto (Osa Menor) está conformado por los puntos 1 a 7 y las líneas 1 a 6, y la segunda columna de\(K\) define al segundo objeto (Osa Mayor) como puntos 8 a 14 y líneas 7 a 12.


