5.7: Proyecciones
- Page ID
- 82361
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Las pantallas de computadora y las impresoras son dispositivos de visualización bidimensionales. Debemos de alguna manera convertir imágenes tridimensionales a dos dimensiones para poder mostrarlas. Esta tarea la realiza otro tipo de operador matricial llamado proyección.
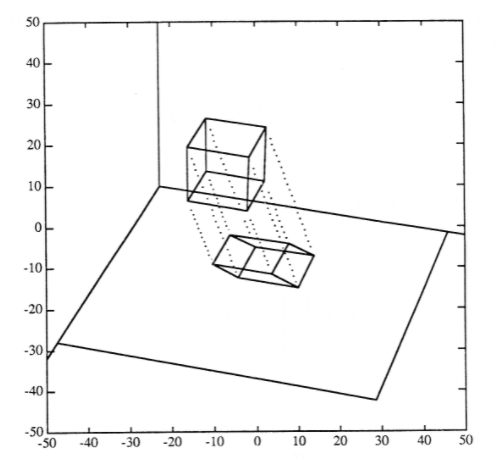
Para construir una proyección, primero elegimos un plano de proyección en el espacio tridimensional del objeto que deseamos visualizar. Todos los puntos del objeto se proyectan entonces sobre el plano. Existen muchos tipos diferentes de proyecciones, correspondientes a diversas reglas geométricas para mapear puntos en el espacio sobre un plano. Comenzamos con la proyección paralela ilustrada en la Figura 1, en donde las líneas punteadas entre los puntos y sus proyecciones en el plano son todas paralelas entre sí. Estas líneas punteadas se llaman proyectores.
Rango
El plano de proyección se llama el rango de la proyección. Asumiremos por ahora que el plano de proyección pasa por el origen. Si no lo hace, posteriormente podremos componer las traducciones necesarias con nuestra proyección. Se requieren tres puntos, no todos en una línea, para determinar un plano. Tomaremos el origen como uno de los puntos y supondremos que los otros dos puntos son los vectores\(r_1\) y\(r_2\). A partir de estos vectores, formamos la matriz
\[\mathrm{R}=\left[\mathrm{r}_{1} \mathrm{r}_{2}\right] \nonumber \]
que determina el alcance de la proyección.
Espacio nulo
Para completar la especificación de la proyección paralela, debemos especificar la dirección de los proyectores. La línea que atraviesa el origen en esta dirección se denomina espacio nulo de la proyección. Tenga en cuenta que cualquier línea en el objeto tridimensional que sea paralela al espacio nulo desaparecerá a un punto cuando se proyecte. El espacio nulo puede especificarse mediante un vector\(n\) que apunta en la dirección de los proyectores.
Proyección ortogonal
Si el espacio nulo es perpendicular al rango, decimos que la proyección es una proyección ortogonal. El operador de matriz para proyección ortogonal es una función del rango. Si asumimos que\(R\) se especifica en coordenadas tridimensionales (¡no homogéneas!) , tenemos la siguiente definición para la proyección ortogonal sobre el rango de\(R\):
\[\mathrm{P}(\mathrm{R})=\mathrm{R}\left(\mathrm{R}^{T} \mathrm{R}\right)^{-1} \mathrm{R}^{T} \in \mathscr{R}^{3 \times 3} \nonumber \]
En coordenadas homogéneas, incorporamos esta matriz de proyección 3×3 en la transformación general 4×4:
\ [\ mathrm {P} _ {h} (\ mathrm {R}) =\ left [\ begin {array} {ll}
\ mathrm {P} (\ mathrm {R}) & 0\\
0^ {T} & 1
\ end {array}\ derecha]\ nonumber\]
Supongamos que elegimos el\(x−y\) plano como nuestro plano de proyección. Vectores\(r_1\) y\(r_2\) pueden ser dos puntos cualesquiera en el plano (además del origen), así que tomemos
\ [\ mathrm {r} _ {1} =\ left [\ begin {array} {l}
1\\
0\
0
\ end {array}\ right],\ mathrm {r} _ {2} =\ left [\ begin {array} {l}
1\\
1\
0
\ end {array}\ derecha]\ nonumber\]
Entonces la matriz de rango es
\ [\ mathrm {R} =\ left [\ begin {array} {ll}
1 & 1\\
0 & 1\\
0 & 0
\ end {array}\ derecha]\ nonumber\]
La proyección ortogonal mirando hacia abajo en el\(x−y\) plano desde el eje z es
\ [\ begin {align}
\ mathrm {P} (\ mathrm {R}) &=\ left [\ begin {array} {ll}
1 & 1\\
0 & 1\\
0 & 0
\ end {array}\ derecha]\ left (\ left [\ begin {array} {lll}
1 & 0 & 0\\
1 & 0 & 1 & 0
\ end {array}\ right]\ left [\ begin {array} {ll}
1 & 1\\
0 & 1\\
0 & 0
\ end {array}\ right]\ right) ^ {-1}\ left [\ begin {array} {lll}
1 & 0 & 0\\
1 & 0 & 1 & 0
\ end {array}\ right]\ nonumber\\
&=\ left [\ begin {array} {lll}
1 & 0 & 0\\
0 & 1 & 0\\
0 & 0 & 0 & 0
\ end {array}\ right].
\ end {align}\ nonumber\]
En coordenadas homogéneas,
\ [\ mathrm {P} _ {h} (\ mathrm {R}) =\ left [\ begin {array} {llll}
1 & 0 & 0 & 0 &
0\\ 0 & 1 & 0 &
0 & 0 & 0 & 0 & 0 &
0 & 0 & 0 & 1
\ end {array}\ derecha]\ nonumber\]
Deje que los vectores\ (\ mathrm {r} _ {1} =\ left [\ begin {array} {l}
2\\
0\
0
\ end {array}\ right]\) y\ (\ mathrm {r} _ {2} =\ left [\ begin {array} {l}
0\\
3\
0
\ end {array}\ right]\) especifiquen el rango de un proyección ortogonal. Encuentra P (R) y P\(_h\) (R). Compare con el Ejemplo 1 y explique cualquier similitud.
En el capítulo sobre álgebra lineal aprendiste que la proyección de\(w\) onto\(x\) viene dada por
\[\mathrm{z}=\frac{(\mathrm{x}, \mathrm{w}) \mathrm{x}}{(\mathrm{x}, \mathrm{x})} \nonumber \]
Se trata de una proyección ortogonal de\(w\) sobre una línea, pero está estrechamente relacionada con la proyección hacia el plano que se acaba de describir. Para ver la similitud, trabajemos\(z\) un poco en la expresión:
\ [\ begin {align}
\ mathbf {z} &=\ frac {\ mathrm {x} (\ mathrm {x},\ mathrm {w})} {(\ mathrm {x},\ mathrm {x})}\ nonumber\\
&=\ mathrm {x} (\ mathrm {x},\ mathrm {x}) ^ {-1} (\ mathrm {x}) ^ {-1} (\ mathrm {x}) ^ {-1} (\ mathrm {x}) ^ {{x},\ mathrm {w})\ nonumber\\
&=\ mathrm {x}\ izquierda (\ mathrm {x} ^ {T}\ mathrm {x}\ derecha) ^ {-1}\ izquierda (\ mathrm {x} ^ {T}\ mathrm {w}\ derecha)\ nonumber\\
&=\ izquierda [\ mathrm {x}\ izquierda (\ mathrm {x} ^ {T}\ mathrm {x}\ derecha) ^ {-1}\ mathrm {x} ^ {T}\ derecha]\ mathrm {w}\ nonumber\\
&=\ mathrm {P} (\ mathrm {x})\ mathrm {w}.
\ end {align}\ nonumber\]
Entonces vemos que se puede escribir de la misma manera que la proyección sobre el plano. La única diferencia es que el rango es ahora unidimensional y especificado por\(x\) in place of\(R\).
Proyección Oblicua
De manera más general, podemos tener un espacio nulo\(n\) que no es perpendicular al rango R. La proyección que se muestra en la Figura 1 es una proyección oblicua. Una vez más comenzamos con coordenadas no homogéneas para\(n\) y\(R\) y escribimos la proyección oblicua 3×3 como
\[\mathrm{E}(\mathrm{R}, \mathrm{n})=\mathrm{R}\left\{\mathrm{R}^{T}[I--P(n)] \mathrm{R}\right\}^{-1} \mathrm{R}^{T}[I--P(n)] \nonumber \]
donde
\[\mathrm{P}(\mathrm{n})=\mathrm{n}\left(\mathrm{n}^{T} \mathrm{n}\right)^{-1} \mathrm{n}^{T}=\frac{\mathrm{n} \mathrm{n}^{T}}{\|\mathrm{n}\|^{2}} \nonumber \]
Al igual que con la proyección ortogonal, podemos volver a coordenadas homogéneas mediante
\ [\ mathrm {E} _ {h} (\ mathrm {R},\ mathrm {n}) =\ left [\ begin {array} {lll}
\ mathrm {E} (\ mathrm {R} &\ mathrm {n}) & 0\
\ mathrm {O} ^ {T} & & 1
\ end {array}\ derecha]\ nonumber\]
Probar e interpretar las siguientes propiedades de las proyecciones paralle1 (tanto ortogonales como oblicuas):
- P\(^2\) = P; E\(^2\) = E.
- \(PR\)=R;\(ER\) =R.
- \(En\)=0;\(Pn\) =0. (Primero mostrar que R\(^T\) n=0 cuando\(n\) es ortogonal a\(R\)).
Visualización desde Proyecciones
Incluso después de haber utilizado una proyección, los puntos de imagen están en coordenadas homogéneas tridimensionales. ¿Cómo entonces los mostramos en una pantalla bidimensional? Si hubiéramos elegido el\(x−y\) plano como el rango de nuestra proyección, podríamos dejar que el dispositivo de salida represente el\(x−y\) plano e ignorar la coordenada z de cada punto. Las coordenadas z de la imagen proyectada serían todas 0 de todos modos ya que los puntos proyectados estarían en el\(x−y\) plano. La cuarta coordenada de 1 también puede ignorarse para su visualización. Pero aunque el plano de proyección no sea el\(x−y\) plano, podemos realizar una rotación para alinear los dos planos y nuevamente dejar que el dispositivo de salida represente el\(x−y\) plano.
Proyecciones en perspectiva
Para obtener una proyección en perspectiva, primero elegimos un plano de proyección como hicimos para proyecciones paralelas. En lugar de elegir un espacio nulo paralelo a todos los proyectores, ahora elegimos un punto de vista. Todos los proyectores pasan por el punto de vista en una proyección en perspectiva, como se muestra en la Figura 2. Para un punto de vista\(z=d\) en el eje z y un plano de proyección que coincide con el\(x−y\) plano, el operador homogéneo tridimensional para proyección en perspectiva es
\ [\ mathbf {M} (d) =\ left [\ begin {array} {llll}
1 & 0 & 0 & 0\\
0 & 1 & 0 & 0 & 0 &
0\\ 0 & 0 & 0 &
0 &\ 0 &\ frac {-1} {d} & 1
\ end {array}\ derecha]\ nonumber\]
Lo primero que debes notar de la proyección en perspectiva M (\(d\)) es que viola la estructura dada en la Ecuación 2 de “Gráficos vectoriales: Coordenadas Homogéneas Tridimensionales” al tener la posición 4,3 igual a −\(\frac{1}{d}\) en lugar de a 0. Esto significa que las cuartas coordenadas no permanecerán 1 en la nueva matriz de puntos
\[\mathrm{G}_{\text {new }}=\mathbf{M}(d) \mathbf{G} \nonumber \]
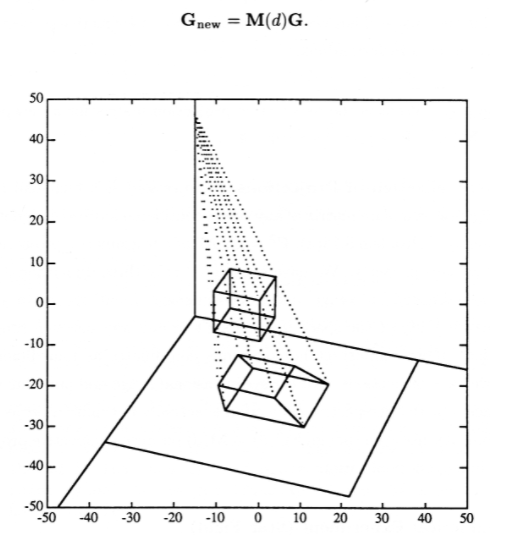
Esta situación se interpreta en el sentido de que el nuevo punto\((x,y,z,w)\) debe ser renormalizado a\((\frac{x}{w}, \frac{y}{w} \frac{z}{w}1)\) antes de que la operación se considere completa. La renormalización agrega otro paso computacional al proceso de transformación de imágenes. Esto es indeseable, pero estamos atrapados en ello si queremos incluir proyecciones de perspectiva en nuestro repertorio de transformaciones. Tenga en cuenta que la renormalización es un proceso punto por punto ya que\(w\) puede ser diferente para cada punto.
¿Cómo afecta la renormalización a la composición de los operadores? Podríamos esperar que, cada vez que realicemos una operación que requiera renormalización, nos veamos obligados a detenernos y hacer la renormalización antes de continuar con otras operaciones. En este sentido somos afortunados: podemos pospongamos la renormalización hasta que todas las transformaciones estén completas y renormalizar una vez justo antes de mostrar la imagen. Así somos capaces de componer proyecciones de perspectiva a voluntad con otras transformaciones.
¿Cuál es la matriz de proyección de perspectiva para un punto de vista al infinito, M (\(\infty\))? Interpretar el resultado.
Generalización de Proyecciones
“Proyección” es un término técnico en álgebra lineal. Una matriz cuadrada de cualquier tamaño se considera una proyección si obedece a la propiedad del Ejercicio 2 (a), P\(^2\) =P Todas nuestras matrices de proyección geométrica tienen esta propiedad. Hemos considerado solo espacios tridimensionales con un rango bidimensional y un espacio nulo unidimensional. En general, la dimensionalidad del espacio puede dividirse de cualquier manera entre rango y espacio nulo. Si reinterpretamos coordenadas homogéneas como espacio de cuatro dimensiones, tenemos proyecciones con rango tridimensional y espacio nulo unidimensional, pero la proyección en perspectiva en realidad no es del todo una proyección en el sentido técnico a pesar de que M\(^2(d)\) =M (\(d\)) porque la proyección en perspectiva también incluye la renormalización.


