7.1: Introducción
- Page ID
- 82316
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Agradecimiento: El libro de Richard Hamming, Information Theory and Coding, Prentice-Hall, Nueva York (1985) y las notas inéditas de C. T. Mullis han influido en nuestro tratamiento de los códigos binarios. El experimento numérico fue desarrollado por Mullis.
Utilizamos este capítulo para introducir a los estudiantes en el paradigma de la comunicación y mostrar cómo los símbolos arbitrarios pueden ser representados por códigos binarios. Estos símbolos y sus códigos binarios correspondientes pueden ser instrucciones informáticas, datos enteros, aproximaciones a datos reales, etc.
Desarrollamos algunos códigos de árbol ad hoc para representar información y luego desarrollamos códigos Huffman para optimizar el uso de bits. Los códigos Hamming agregan bits de verificación a una palabra binaria para que los errores puedan ser detectados y corregidos. El experimento numérico hace que los estudiantes diseñen un código Huffman para codificar la dirección de Gettysburg de Lincoln.
Introducción
Estaría estirando nuestra imaginación sugerir que Sir Francis tenía audio digital en su mente (sic) cuando escribió las palabras proféticas
Sir Francis Bacon, 1623... un hombre puede expresar y significar las intenciones de su mente, a cualquier distancia... por... objetos... capaces de una doble diferencia unísonamente. “
Sin embargo, esta idea básica forma la base de todo lo que hacemos en computación digital, comunicaciones digitales y audio/video digital. En 1832, Samuel F. B. Morse utilizó la misma idea para proponer que las palabras de telegrama se codificaran en direcciones binarias o códigos binarios que pudieran transmitirse a través de líneas telegráficas y decodificarse en el extremo receptor para desentrañar el telegrama. Morse abandonó su esquema, ilustrado en la Figura 1, por ser demasiado complicado y, en 1838, propuso su legendario código Morse para codificar letras (en lugar de palabras) en objetos (puntos, guiones, espacios) capaces de una triple diferencia única (sic).
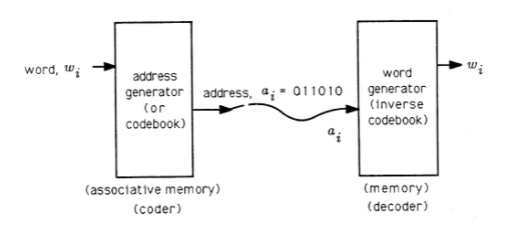
La idea básica de la Figura 1 se utiliza hoy en día en sistemas criptográficos, donde la “dirección\(a_i\)" es una versión cifrada de un mensaje\(w_i\); en cuantificadores vectoriales, donde la “dirección\(a_i\)" es la dirección de una aproximación cercana a los datos\(w_i\); en las transmisiones codificadas por satélite, donde el” address\(a_i\) "es una palabra de datos\(w_i\) más bits de comprobación de paridad para detectar y corregir errores; en sistemas de audio digital, donde la “dirección\(a_i\)" es un tramo de música digitalizada y codificada; y en memorias de computadora, donde\(a_i\) está una dirección (una versión codificada de una palabra de memoria) y \(w_i\)es una palabra en la memoria.
En este capítulo se estudian tres cuestiones fundamentales en la construcción de direcciones binarias o códigos binarios. Primero, ¿qué son los esquemas plausibles para mapear símbolos (como palabras, letras, instrucciones informáticas, voltajes, presiones, etc.) en códigos binarios? Segundo, ¿cuáles son los esquemas plausibles para codificar símbolos probables con palabras binarias cortas y símbolos improbables con palabras largas para minimizar el número de dígitos binarios (bits) requeridos para representar un mensaje? Tercero, ¿qué son los esquemas plausibles para “codificar” palabras binarias en palabras binarias más largas que contienen “bits redundantes” que pueden usarse para detectar y corregir errores? Estas no son preguntas nuevas. Han ocupado la mente de muchos grandes pensadores. Sir Francis reconoció que los mensajes arbitrarios tenían representaciones binarias. Alan Turing, Alonzo Church y Kurt Goedel estudiaron códigos binarios para cálculos en su estudio de números computables y algoritmos. Claude Shannon, R. C. Bose, Irving Reed, Richard Hamming y muchos otros han estudiado los códigos de control de errores. Shannon, David Huffman y muchos otros han estudiado el problema de codificar eficientemente la información.
En este capítulo esbozamos las ideas principales en la codificación binaria e ilustramos el papel que juega la codificación binaria en las comunicaciones digitales. En sus posteriores cursos de ingeniería eléctrica e informática estudiará circuitos integrados para codificadores y decodificadores de edificios y modelos matemáticos para diseñar buenos códigos.


