7.2: El paradigma de la comunicación
- Page ID
- 82347
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Un paradigma es un patrón de ideas que forman la base de un cuerpo de conocimiento. Un paradigma para la teoría de la (tele) comunicación es un patrón de bloques básicos que pueden aplicarse a los problemas duales de (i) transmitir información de manera confiable de fuente a receptor a alta velocidad o (ii) almacenar información de manera confiable de fuente a memoria a alta densidad. La comunicación de alta velocidad nos permite acomodar muchas fuentes de baja velocidad (como audio) o una fuente de alta velocidad (como video). El almacenamiento de alta densidad nos permite almacenar una gran cantidad de información en un espacio pequeño. Por ejemplo, un disquete típico de 1.2 Mbytes almacena\(9.6×10^6\) bits de información, mientras que un CD típico almacena aproximadamente\(2×10^9\) bits, lo suficiente para una hora de sonido de alta calidad.
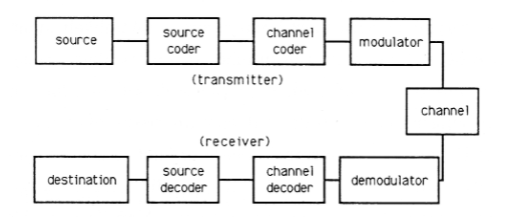
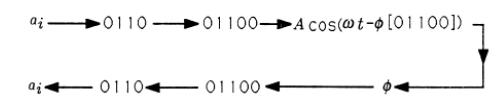
La Figura 1 ilustra los bloques de construcción básicos que se aplican a cualquier problema en la teoría de la (tele) comunicación. La fuente es una fuente arbitraria de información. Puede ser el voltaje variable en el tiempo en la salida de un sensor de vibración (como un acelerómetro integrador para medir el movimiento o un micrófono para medir la presión del sonido); pueden ser las cargas almacenadas en la matriz CCD de una cámara de estado sólido; pueden ser las direcciones generadas a partir de una secuencia de pulsaciones de teclas en un terminal de computadora; puede ser una secuencia de instrucciones en un programa de computadora. El codificador fuente es un dispositivo para convertir salidas de fuente primitivas en representaciones más eficientes. Por ejemplo, en un estudio de grabación, el codificador fuente convertiría voltajes analógicos en aproximaciones digitales usando un convertidor A/D; un codificador de fuente elegante usaría un convertidor A/D elegante que cuantificaba finamente los valores analógicos probables y cuantificaba crudamente los valores improbables. Si la fuente es una fuente de símbolos discretos como letras y números, entonces un código fuente elegante asignaría secuencias binarias cortas a símbolos probables (como\(e\)) y secuencias binarias largas a símbolos improbables (como\(z\)). “El codificador de canal agrega “" bits redundantes "” a la salida binaria del codificador de origen para que puedan detectarse y corregirse errores de transmisión o almacenamiento.” En el ejemplo más simple, una cadena binaria de la forma 01001001 tendría un bit extra de 1 agregado para dar paridad par (un número par de l's) a la cadena; la cadena 10110111 tendría un bit extra de 0 agregado para preservar la paridad par. Si se introduce un error de bit en el canal, entonces la paridad es impar y el receptor sabe que se ha producido un error. El modulador toma salidas del codificador de canal, un flujo de dígitos binarios, y construye una forma de onda analógica que representa un bloque de bits. Por ejemplo, en un Modem de 9600 baudios, se utilizan cinco bits para determinar una de\(2^5=32\) las fases que se utilizan para modular la señal Acos (ωt+φ) Acos (ωt+φ). Cada posible cadena de cinco bits tiene su propia fase personalizada\(\phi\), y esta fase se puede determinar en el receptor. La señal\(A \cos (\omega t+\phi)\). \(A \cos (\omega t+\phi)\)es una señal analógica que puede transmitirse a través de un canal (como una línea telefónica, un enlace de microondas o un cable de fibra óptica). El canal tiene un ancho de banda finito, lo que significa que distorsiona las señales, y está sujeto a ruido o interferencia de otra radiación electromagnética. Por lo tanto, la información transmitida llega al demodulador en forma imperfecta. El demodulador utiliza filtros coincidentes con las señales moduladas para demodular la fase y buscar el flujo de bits correspondiente. El decodificador de canal convierte el flujo de bits codificado en el flujo de bits de información, y el decodificador fuente busca el símbolo correspondiente. Esta secuencia de pasos se ilustra simbólicamente en la Figura 7.3.
En tus cursos posteriores sobre teoría de la comunicación estudiarás cada bloque de la Figura 1 en detalle. Encontrarás que cada fuente de información tiene una complejidad característica, llamada entropía, que determina la velocidad mínima a la que se deben generar los bits para representar la fuente. También encontrará que cada canal de comunicación tiene una tolerancia característica para bits, llamada capacidad de canal. Esta capacidad depende de la relación señal/ruido y el ancho de banda. Cuando la capacidad del canal excede la entropía de origen, entonces puedes transmitir información de manera confiable; si no lo hace, entonces no puedes.


