2.3: Interpretación de la Gráfica de una Función

En la sección anterior, comenzamos con una función y luego dibujamos la gráfica de la función dada. En esta sección, comenzaremos con la gráfica de una función, luego haremos una serie de interpretaciones basadas en la gráfica dada: evaluaciones de funciones, el dominio y rango de la función, y resolviendo ecuaciones y desigualdades.

La prueba de línea vertical

Considere la gráfica de la relación R que se muestra en la Figura\(\PageIndex{1}\) (a). Recordemos que antes definimos una relación como un conjunto de pares ordenados. Seguramente, la gráfica que se muestra en la Figura\(\PageIndex{1}\) (a) es un conjunto de pares ordenados. En efecto, se trata de un conjunto infinito de pares ordenados, tantos que la gráfica es una curva sólida.

En la Figura\(\PageIndex{1}\) (b), tenga en cuenta que podemos dibujar una línea vertical que corta la gráfica más de una vez. En la Figura\(\PageIndex{1}\) (b), hemos dibujado una línea vertical que corta la gráfica en dos lugares, una en\(\left(x, y_{1}\right)\), luego otra vez en\(\left(x, y_{2}\right)\), como se muestra en la Figura\(\PageIndex{1}\) (c). Esto significa que el objeto de dominio x está emparejado con dos objetos de rango diferentes, es decir,\(y_{1}\) y\(y_{2}\), por lo que la relación R no es una función.

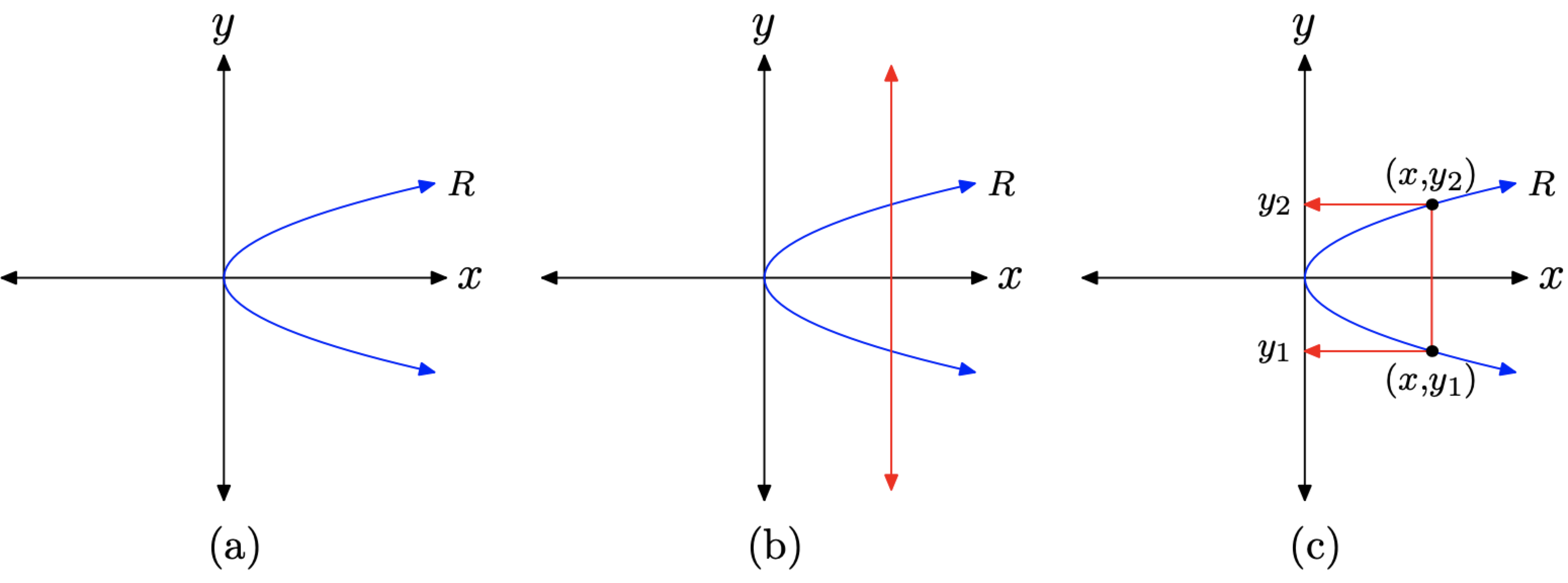
Figura\(\PageIndex{1}\). Explicación de la prueba de línea vertical para funciones.

Recordemos la definición de una función.

Definición

Una relación es una función si y solo si cada objeto en su dominio está emparejado con uno y solo un objeto en su rango.

Considera el diagrama de mapeo en la Figura\(\PageIndex{2}\), donde hemos utilizado flechas para indicar los pares ordenados\(\left(x, y_{1}\right)\) y\(\left(x, y_{2}\right)\) en la Figura\(\PageIndex{1}\) (c). Tenga en cuenta que x, un objeto en el dominio de R, se mapea a dos objetos en el rango de R, a saber\(y_{1}\) y\(y_{2}\). De ahí que la relación R no sea una función.

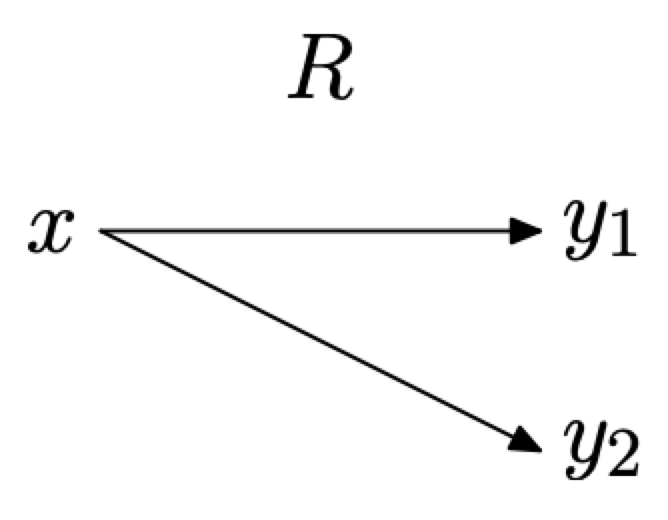
Figura\(\PageIndex{2}\). Un diagrama de mapeo que representa los puntos\(\left(x, y_{1}\right)\) y\(\left(x, y_{2}\right)\) en la Figura\(\PageIndex{1}\) (c).

Esta discusión lleva al siguiente resultado, llamado prueba de línea vertical para funciones.

La prueba de línea vertical

Si alguna línea vertical corta la gráfica de una relación más de una vez, entonces la relación NO es una función.

De ahí que el círculo representado en la Figura\(\PageIndex{3}\) (a) sea una relación, pero no es la gráfica de una función. Es posible cortar la gráfica del círculo más de una vez con una línea vertical, como se muestra en la Figura\(\PageIndex{3}\) (a). Por otro lado, la parábola que se muestra en la Figura\(\PageIndex{3}\) (b) es la gráfica de una función, pues ninguna línea vertical cortará la gráfica más de una vez.

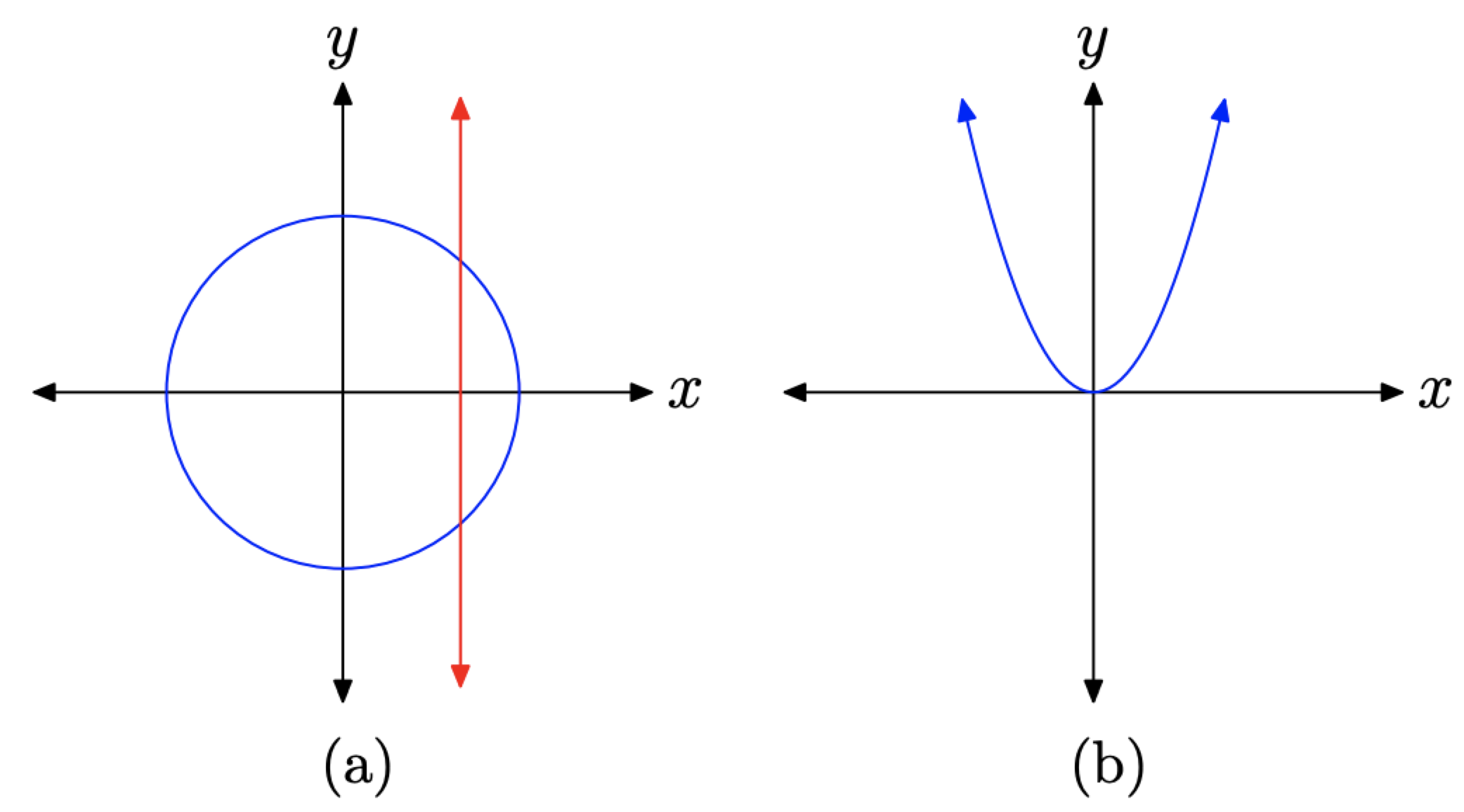
Figura\(\PageIndex{3}\). Utilice la prueba de línea vertical para determinar si la gráfica es la gráfica de una función.

Lectura de la Gráfica para Valores de Función

Sabemos que la gráfica de f que se muestra en la Figura\(\PageIndex{4}\) es la gráfica de una función. Esto lo sabemos porque ninguna línea vertical cortará la gráfica de f más de una vez.

Anteriormente definimos la gráfica de f como el conjunto de todos los pares ordenados\((x, f(x))\), de manera que x está en el dominio de f. En consecuencia, si seleccionamos un punto P en la gráfica de f, como en la Figura\(\PageIndex{4}\) (a), etiquetamos el punto P (x, f (x)). Sin embargo, también podemos etiquetar este punto como\(P(x, y)\), como se muestra en la Figura\(\PageIndex{4}\) (b). Esto lleva a una nueva interpretación de f (x) como el valor y del punto P. Es decir, f (x) es el valor y que se empareja con x.

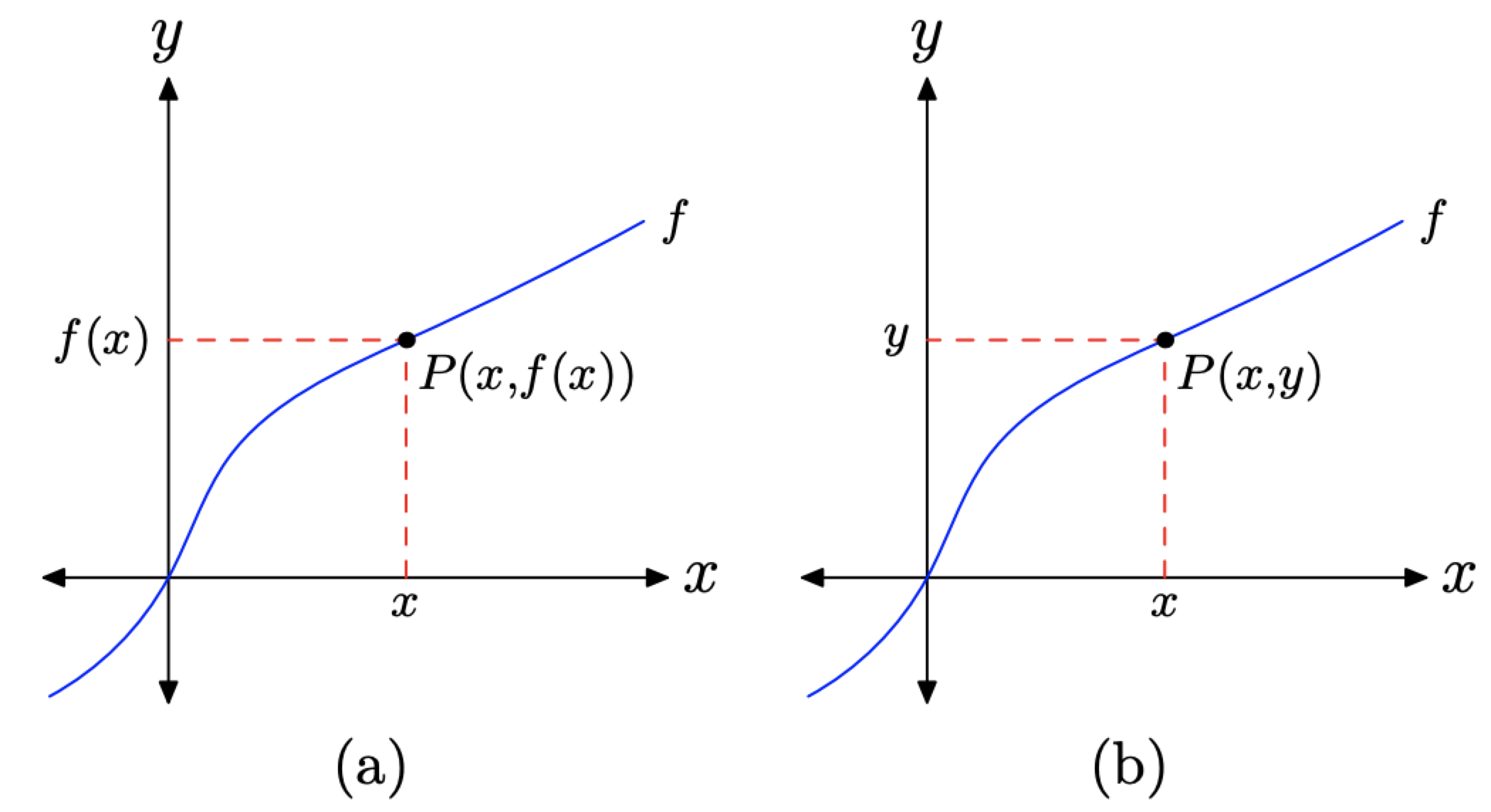
Figura\(\PageIndex{4}\). Lectura de la gráfica de una función.

Definición

f (x) es el valor y que se empareja con x.

Dos comentarios más están en regla. En la Figura\(\PageIndex{4}\) (a), seleccionamos un punto P en la gráfica de f.

1. Para encontrar el valor x del punto P, debemos proyectar el punto P sobre el eje x.
2. Para encontrar f (x), el valor de y que se empareja con x, debemos proyectar el punto P sobre el eje y.

Veamos un ejemplo.

Ejemplo\(\PageIndex{1}\)

Dada la gráfica de f en la Figura\(\PageIndex{5}\) (a), encontrar f (4).

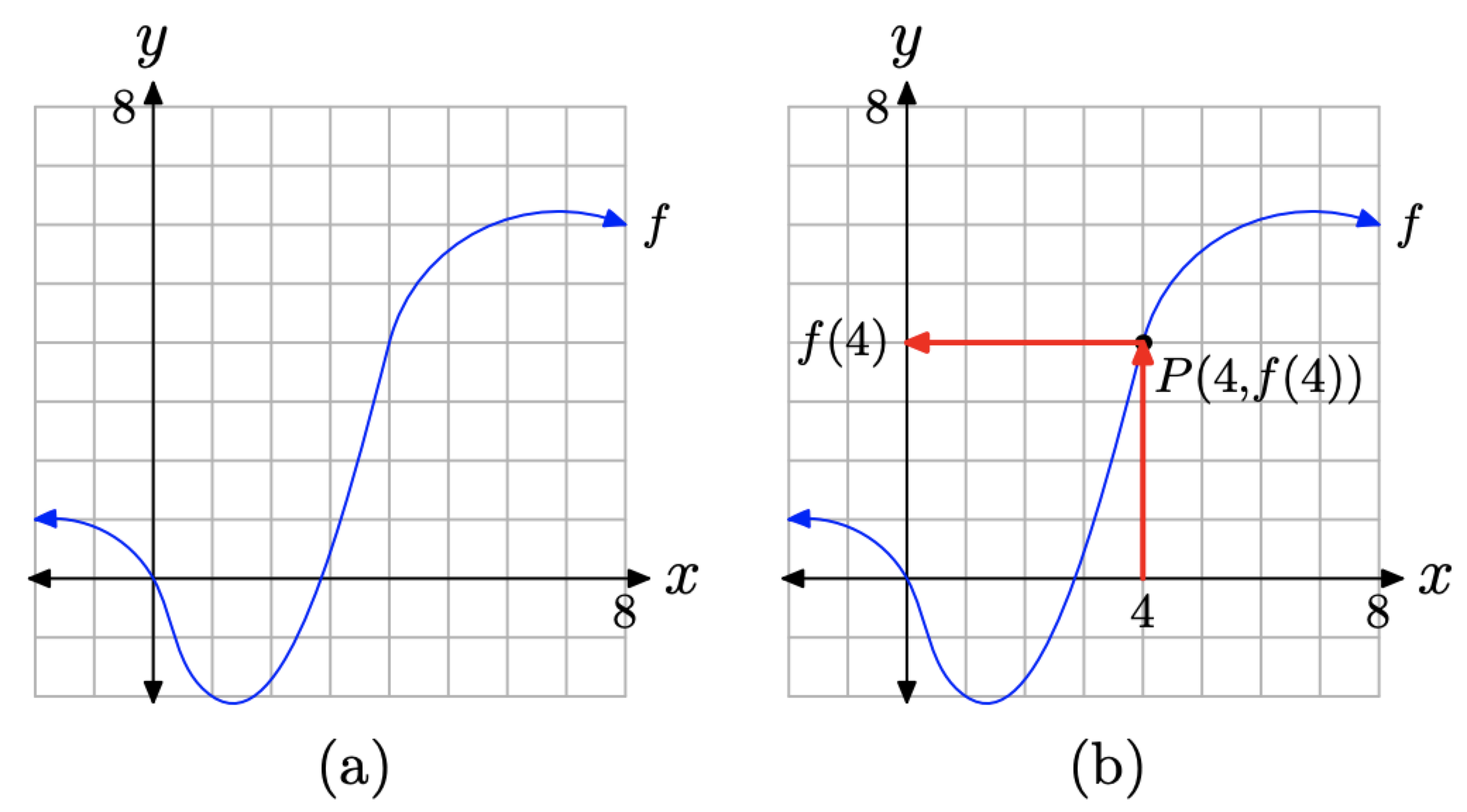
Figura (\ PageIndex {5}\). Encontrar el valor de f (4).

Solución

Primero, tenga en cuenta que la gráfica de f representa una función. Ninguna línea vertical cortará la gráfica de f más de una vez.

Debido a que f (4) representa el valor y que se empareja con un valor x de 4, primero ubicamos 4 en el eje x, como se muestra en la Figura (\ PageIndex {5}\) (b). Luego dibujamos una flecha vertical hasta interceptar la gráfica de f en el punto P (4, f (4)). Finalmente, dibujamos una flecha horizontal desde el punto P hasta interceptar el eje y. La proyección del punto P sobre el eje y es el valor de f (4).

Debido a que tenemos una cuadrícula que muestra una escala en cada eje, podemos aproximar el valor de f (4). Parecería que el valor y del punto P es aproximadamente 4. Así,\(f(4) \approx 4\).

Veamos otro ejemplo.

Ejemplo\(\PageIndex{2}\)

Dada la gráfica de f en la Figura (\ PageIndex {6}\) (a), encuentra f (5).

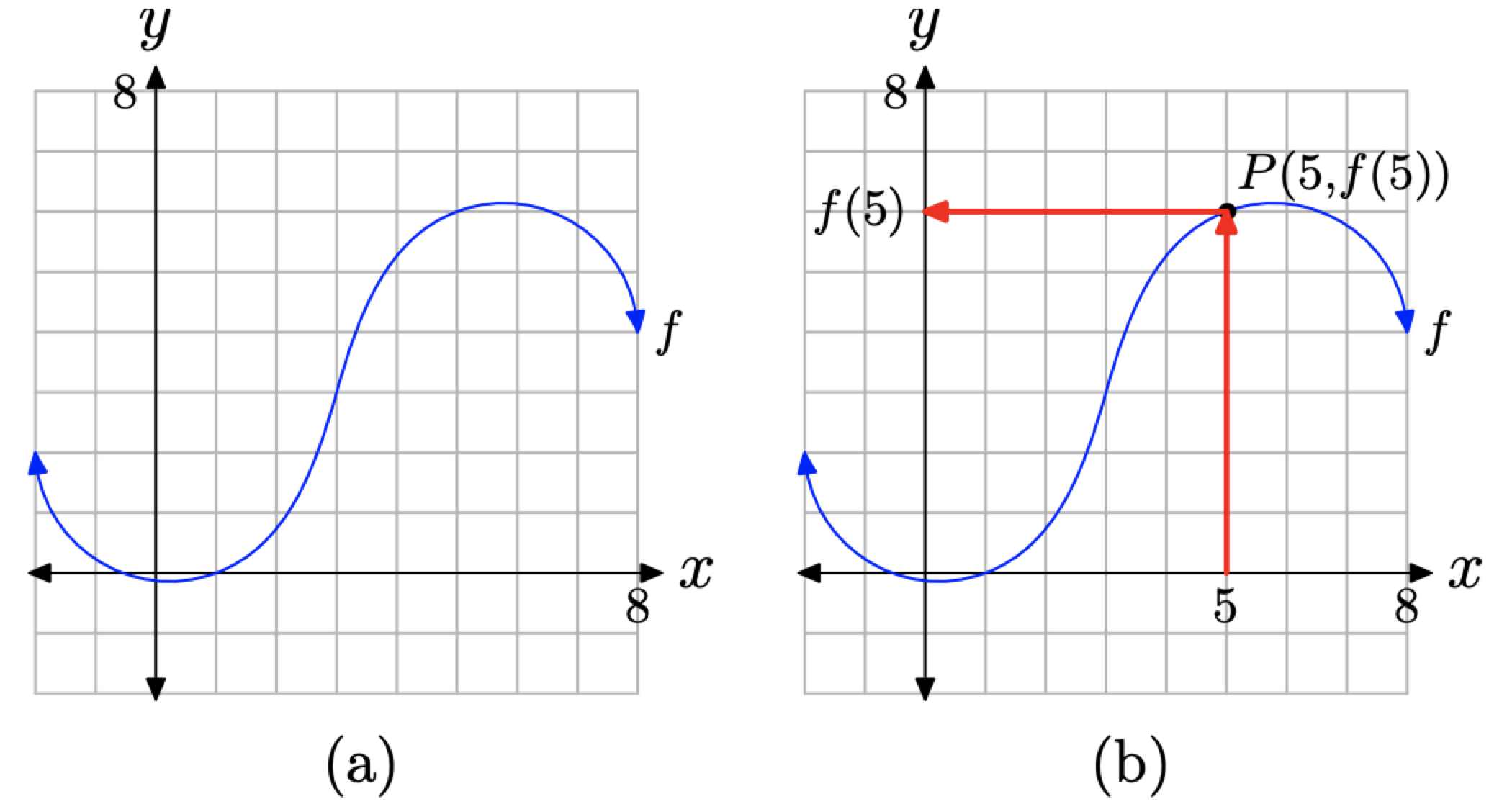
Figura (\ PageIndex {6}\). Encontrar el valor de f (5).

Solución

Primero, tenga en cuenta que la gráfica de f representa una función. Ninguna línea vertical cortará la gráfica de f más de una vez.

Debido a que f (5) representa el valor y que se empareja con un valor x de 5, primero ubicamos 5 en el eje x, como se muestra en la Figura (\ PageIndex {6}\) (b). Luego dibujamos una flecha vertical hasta interceptar la gráfica de f en el punto P (5, f (5)). Finalmente, dibujamos una flecha horizontal desde el punto P hasta interceptar el eje y. La proyección del punto P sobre el eje y es el valor de f (5).

Debido a que tenemos una cuadrícula que muestra una escala en cada eje, podemos aproximar el valor de f (5). Parecería que el valor y del punto P es aproximadamente 6. Así,\(f(5) \approx 6\).

Revertimos la interpretación en otro ejemplo.

Ejemplo\(\PageIndex{3}\)

Dada la gráfica de f en la Figura (\ PageIndex {7}\) (a), ¿para qué valor de x f (x) = −4?

Solución

Nuevamente, la gráfica de la Figura (\ PageIndex {7}\) pasa la prueba de línea vertical y representa la gráfica de una función.

Esta vez, en la ecuación\(f(x) = −4\), se nos da un valor y igual a −4. En consecuencia, debemos revertir el proceso utilizado en Ejemplo\(\PageIndex{1}\) y Ejemplo\(\PageIndex{2}\). Primero ubicamos el valor y −4 en el eje y, luego dibujamos una flecha horizontal hasta interceptar

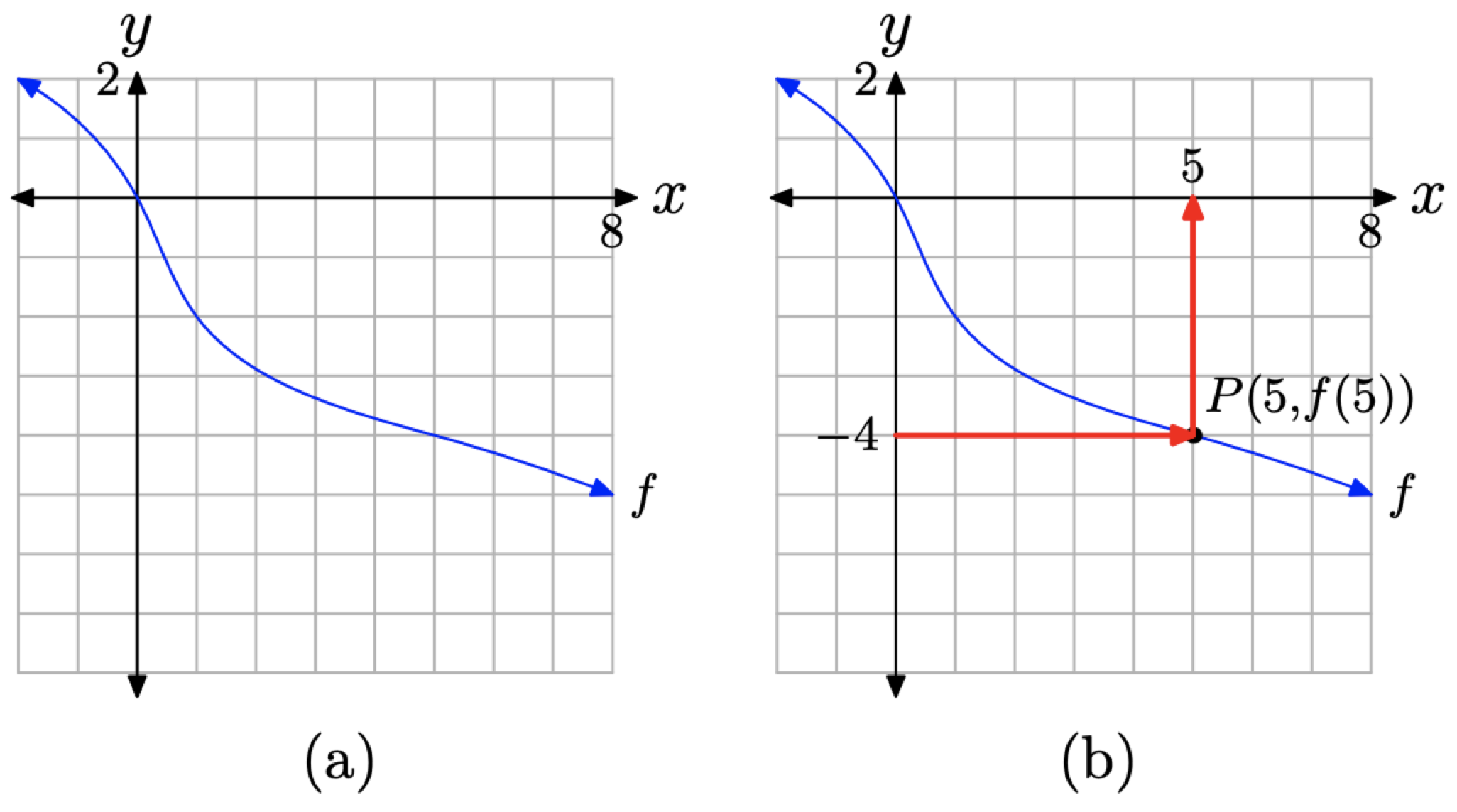
Figura (\ PageIndex {7}\). Encontrar x para que\(f(x) = −4\).

la gráfica de f en P, como se muestra en la Figura (\ PageIndex {7}\) (b). Finalmente, dibujamos una flecha vertical desde el punto P hasta interceptar el eje x. La proyección del punto P sobre el eje x es la solución de\(f(x) = −4\).

Debido a que tenemos una cuadrícula que muestra una escala en cada eje, podemos aproximar el valor x del punto P. Parece que\(x \approx 5\). Así, etiquetamos el punto P (5, f (5)), y la solución de\(f(x) = −4\) es aproximadamente\(x \approx 5\).

Esta solución se puede verificar fácilmente computando f (5). Simplemente comience con 5 en el eje x, luego invierta el orden de las flechas que se muestran en la Figura (\ PageIndex {7}\) (b). Deberías terminar en −4 en el eje y, demostrándolo\(f(5) = −4\).

El dominio y el rango de una función

Podemos usar la gráfica de una función para determinar su dominio y rango. Por ejemplo, considere la gráfica de la función que se muestra en la Figura (\ PageIndex {8}\) (a).

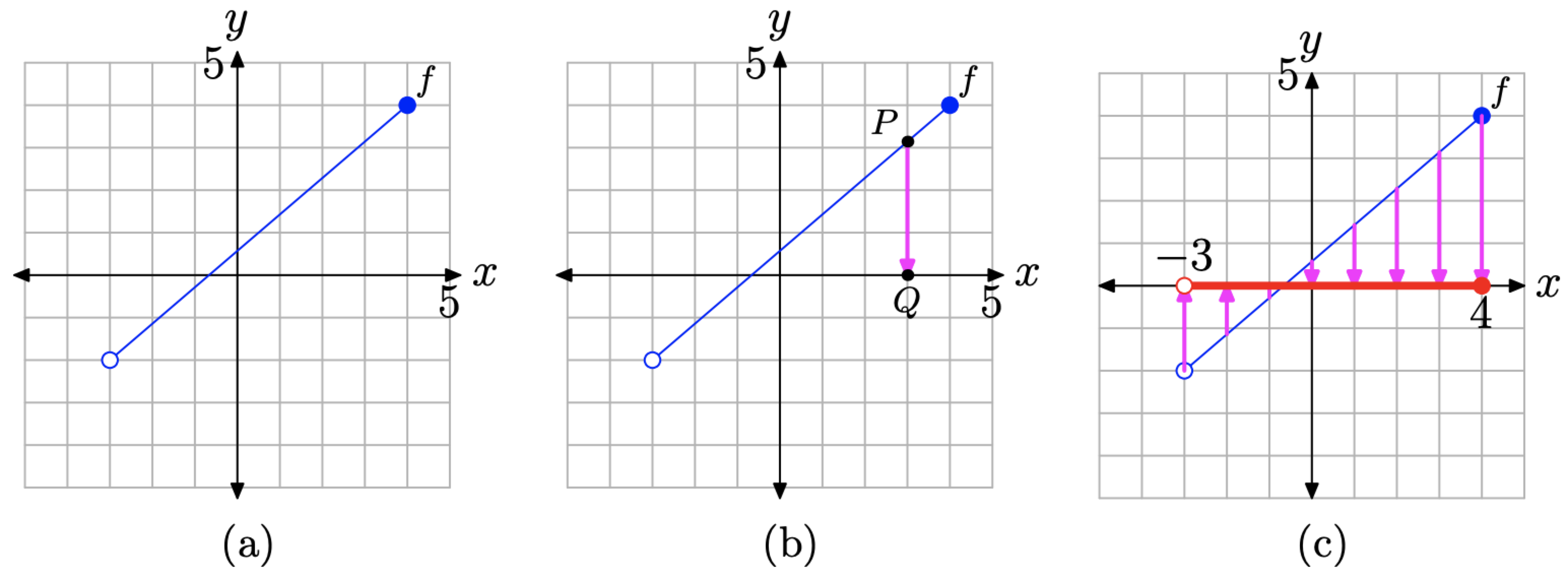
Figura (\ PageIndex {8}\). Determinar el dominio de una función a partir de su gráfica.

Tenga en cuenta que ninguna línea vertical cortará la gráfica de f más de una vez, por lo que la gráfica de f representa una función.

Para determinar el dominio, debemos recopilar los valores x (primeras coordenadas) de cada punto de la gráfica de f. en la Figura (\ PageIndex {8}\) (b), hemos seleccionado un punto P en la gráfica de f, que luego proyectamos sobre el eje x. La imagen de esta proyección es el punto Q, y el valor x del punto Q es un elemento en el dominio de f.

Piense en la proyección que se muestra en la Figura (\ PageIndex {8}\) (b) de la siguiente manera. Imagínese una fuente de luz por encima del punto P. El punto P bloquea la luz y su sombra cae sobre el eje x en el punto Q. Es decir, piense en el punto Q como la “sombra” que el punto P produce cuando se proyecta verticalmente sobre el eje x.

Ahora, para encontrar el dominio de la función f, debemos proyectar cada punto de la gráfica de f sobre el eje x. Aquí está la pregunta: si proyectamos cada punto de la gráfica de f sobre el eje x, ¿qué parte del eje x “quedará en la sombra” cuando se complete el proceso? La respuesta se muestra en la Figura (\ PageIndex {8}\) (c).

En la Figura (\ PageIndex {8}\) (c), tenga en cuenta que la “sombra” creada al proyectar cada punto de la gráfica de f sobre el eje x está sombreada en rojo (una línea más gruesa si está viendo esto en blanco y negro). Esta colección de valores x es el dominio de la función f. Hay tres puntos críticos que necesitamos hacer sobre la “sombra” en el eje x en la Figura (\ PageIndex {8}\) (c).

1. Todos los puntos se encuentran entre\(x = −3\) y\(x = 4\) han sido sombreados en el eje x en rojo.
2. El punto final izquierdo de la gráfica de f es un círculo abierto. Esto indica que no hay ningún punto trazado en este punto final. En consecuencia, no tiene sentido proyectarse sobre el eje x, y esto explica el círculo abierto en el extremo izquierdo de nuestra “sombra” en el eje x.
3. Por otro lado, el punto final derecho de la gráfica de f es un punto final relleno. Esto indica que se trata de un punto trazado y parte de la gráfica de f. En consecuencia, cuando este punto se proyecta sobre el eje x, una sombra cae en x = 4. Esto explica el punto final lleno en el extremo derecho de nuestra “sombra” en el eje x.

Podemos describir los valores x de la “sombra” en el eje x usando la notación set-builder.

\[\text { Domain of } f=\{x :-3<x \leq 4\}\]

Tenga en cuenta que no incluimos −3 en esta descripción porque el extremo izquierdo de la sombra en el eje x es un círculo vacío. Tenga en cuenta que sí incluimos 4 en esta descripción porque el extremo derecho de la sombra en el eje x es un círculo relleno.

También podemos describir los valores x de la “sombra” en el eje x usando notación de intervalo.

\[\text { Domain of } f=(-3,4]\]

Recordamos a nuestros lectores que el paréntesis de la izquierda significa que no estamos incluyendo −3, mientras que el corchete de la derecha significa que estamos incluyendo 4.

Para encontrar el rango de la función, imagínese nuevamente la gráfica de f que se muestra en la Figura\(\PageIndex{9}\) (a). Proceder de manera similar, solo esta vez proyectar puntos en la gráfica de f sobre el eje y, como se muestra en las Figuras\(\PageIndex{9}\) (b) y (c).

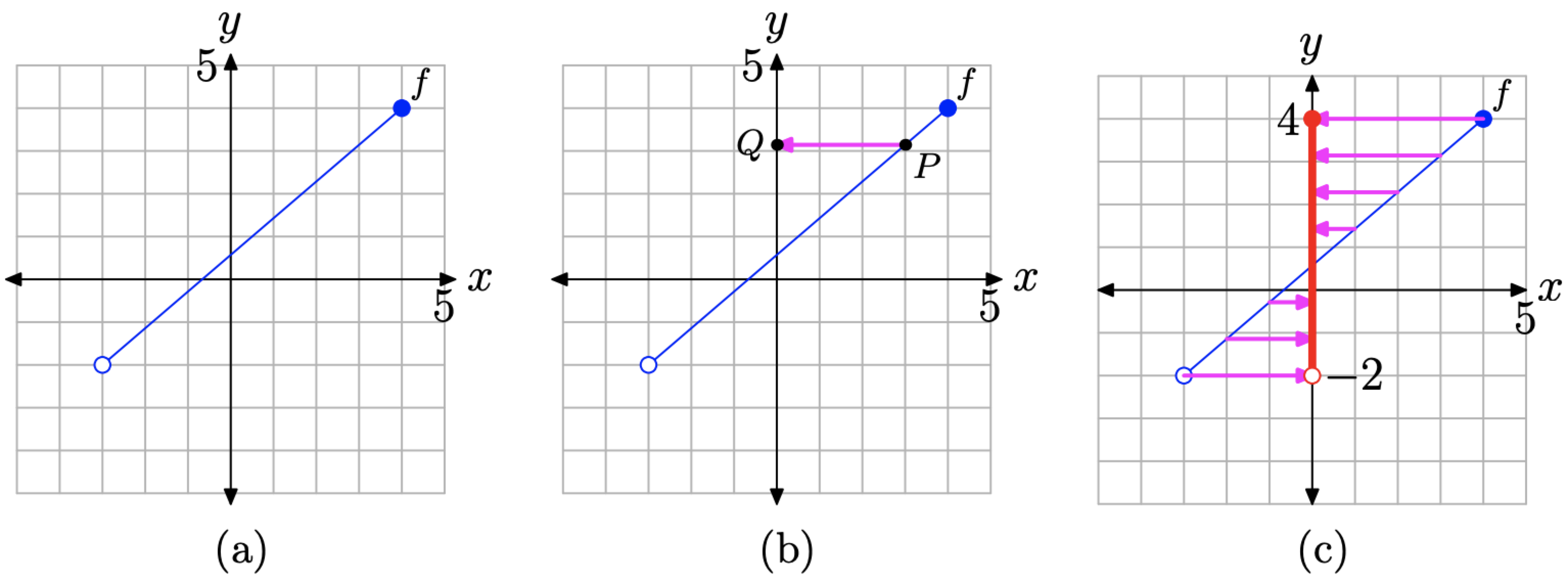
Figura\(\PageIndex{9}\). Determinar el rango de una función a partir de su gráfica.

Observe qué parte del eje y “yace en la sombra” una vez que hayamos proyectado todos los puntos de la gráfica de f sobre el eje y.

1. Todos los puntos que se encuentran entre\(y = −2\) y\(y = 4\) han sido sombreados en el eje y en rojo (un estilo de línea más gruesa si está viendo esto en blanco y negro).
2. El punto final izquierdo de la gráfica de f es un círculo vacío, por lo que no hay punto para proyectarse sobre el eje y. En consecuencia, no hay “sombra”\(y = −2\) en el eje y y el punto se deja sin sombra (un círculo vacío).
3. El punto final derecho de la gráfica de f es un círculo relleno, por lo que hay una “sombra”\(y = 4\) en el eje y y este punto está sombreado (un círculo relleno).

Ahora podemos describir fácilmente el rango tanto en set-builder como en notación de intervalo.

\[\text { Range of } f=(-2,4]=\{y :-2<y \leq 4\}\]

Veamos otro ejemplo.

Ejemplo\(\PageIndex{4}\)

Utilice el generador de conjuntos y la notación de intervalos para describir el dominio y el rango de la función representada por la gráfica en la Figura\(\PageIndex{10}\) (a).

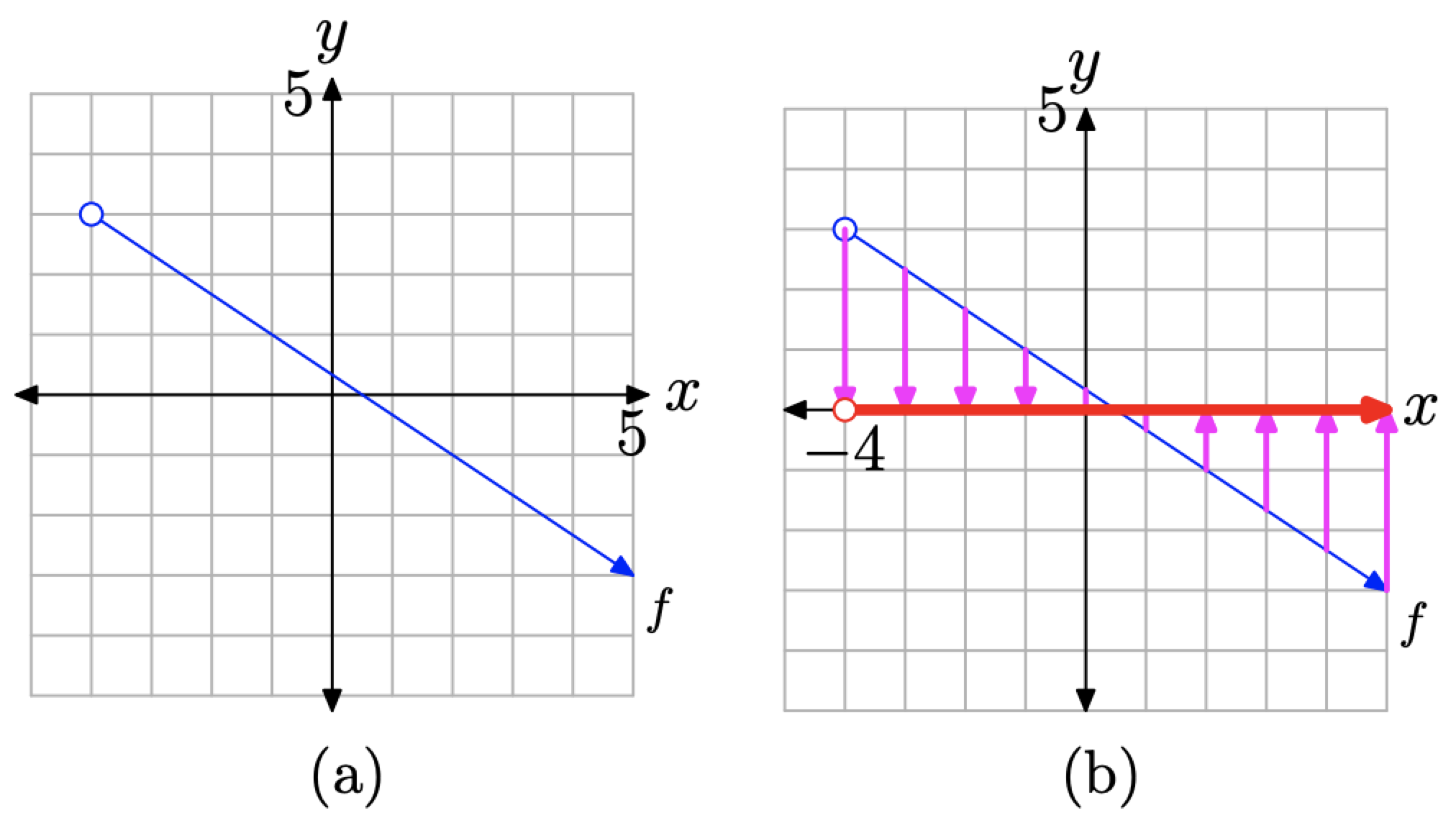
Figura\(\PageIndex{10}\). Determinar el dominio a partir de la gráfica de f.

Solución

Para determinar el dominio de f, proyecte cada punto de la gráfica de f sobre el eje x. Esta proyección está indicada por la “sombra” en el eje x en la Figura\(\PageIndex{10}\) (b). Hay que hacer dos puntos importantes sobre esta “sombra” o proyección.

1. El punto final izquierdo de la gráfica de f está vacío (indicado por el círculo abierto), por lo que no tiene proyección sobre el eje x. Esto se indica mediante un círculo abierto en el extremo izquierdo (at\(x = −4\)) de la “sombra” o proyección en el eje x.

2. La punta de flecha en el extremo derecho de la gráfica de f indica que la gráfica de f continúa hacia abajo y hacia la derecha indefinidamente. En consecuencia, la proyección sobre el eje x es una sombra que se mueve indefinidamente hacia la derecha. Esto se indica con una punta de flecha en el extremo derecho de la “sombra” o proyección en el eje x.

En consecuencia, el dominio de f es la colección de valores x representados por la “sombra” o proyección sobre el eje x. Tenga en cuenta que todos los valores x a la derecha de\(x = −4\) están sombreados en el eje x. En consecuencia,

\[\text { Domain of } f=(-4, \infty)=\{x : x>-4\}\]

Para encontrar el rango, debemos proyectar cada punto en la gráfica de f (redibujado en la Figura\(\PageIndex{11}\) (a)) sobre el eje y. La proyección está indicada por una “sombra” o proyección en el eje y, como se ve en la Figura\(\PageIndex{11}\) (b). Hay que hacer dos puntos importantes sobre esta “sombra” o proyección.

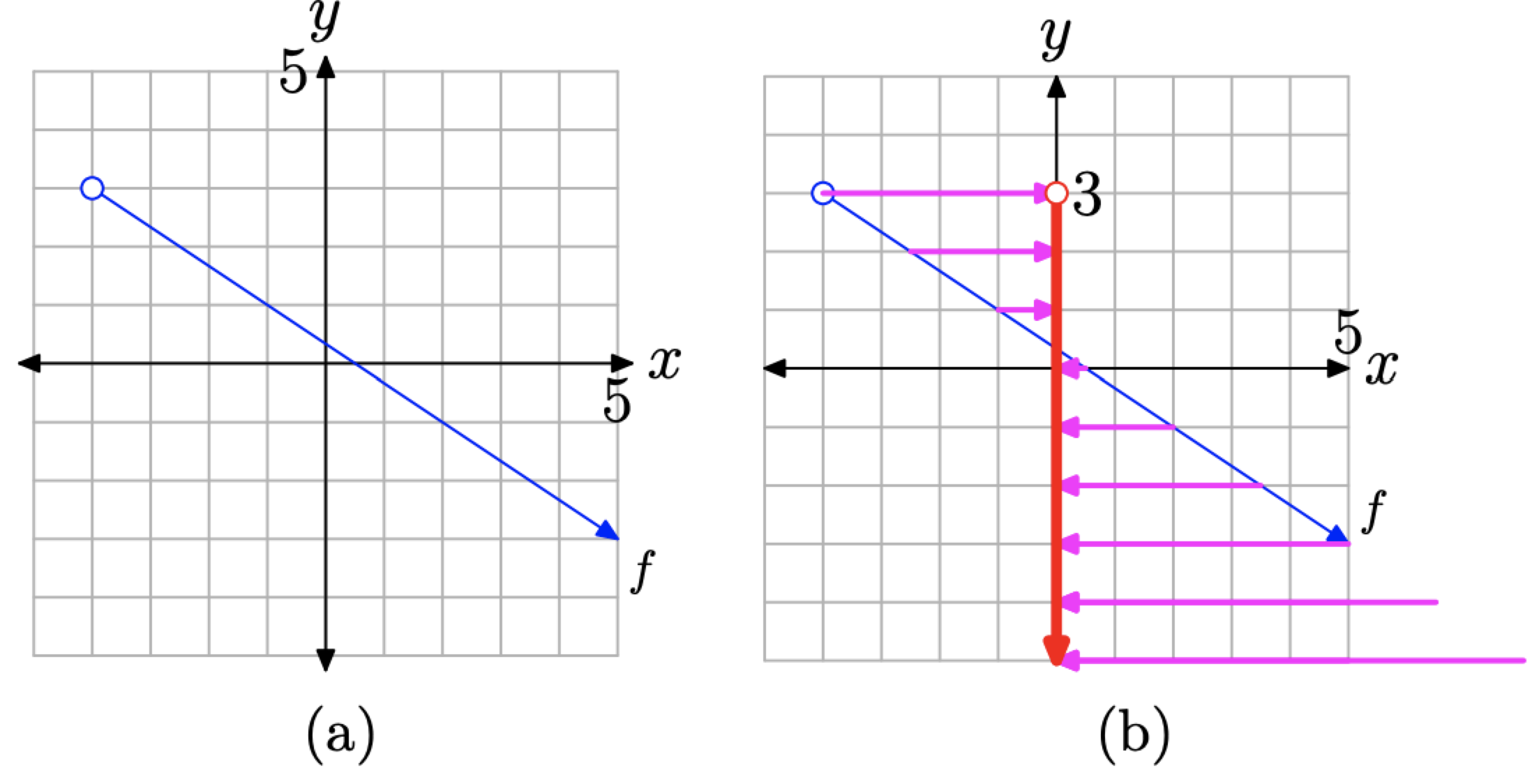
Figura\(\PageIndex{11}\). Determinar el rango a partir de la gráfica de f.

1. El punto final izquierdo de la gráfica de f está vacío (indicado por un círculo abierto), por lo que no tiene proyección sobre el eje y. Esto se indica mediante un círculo abierto en el extremo superior (at\(y = 3\)) de la “sombra” en el eje y.
2. La punta de flecha en el extremo derecho de la gráfica de f indica que la gráfica de f continúa hacia abajo y hacia la derecha indefinidamente. En consecuencia, la proyección de la gráfica de f sobre el eje y es una sombra que se mueve indefinidamente hacia abajo. En la Figura\(\PageIndex{11}\) (b), observe cómo las proyecciones de puntos en la gráfica de f no visibles en la ventana de visualización entran desde la esquina inferior derecha y proyectan “sombras” en el eje y.

En consecuencia, el rango de f es la colección de valores y sombreados en el eje y del sistema de coordenadas mostrado en la Figura\(\PageIndex{11}\) (b). Tenga en cuenta que todos los valores y menores que\(y = 3\) están sombreados en el eje y. Por lo tanto, el rango de f es

\[\text { Range of } f=(-\infty, 3)=\{y : y<3\}\]

Veamos otro ejemplo.

Ejemplo\(\PageIndex{5}\)

Utilice el generador de conjuntos y la notación de intervalos para describir el dominio y el rango de la función representada por la gráfica en la Figura\(\PageIndex{12}\) (a).

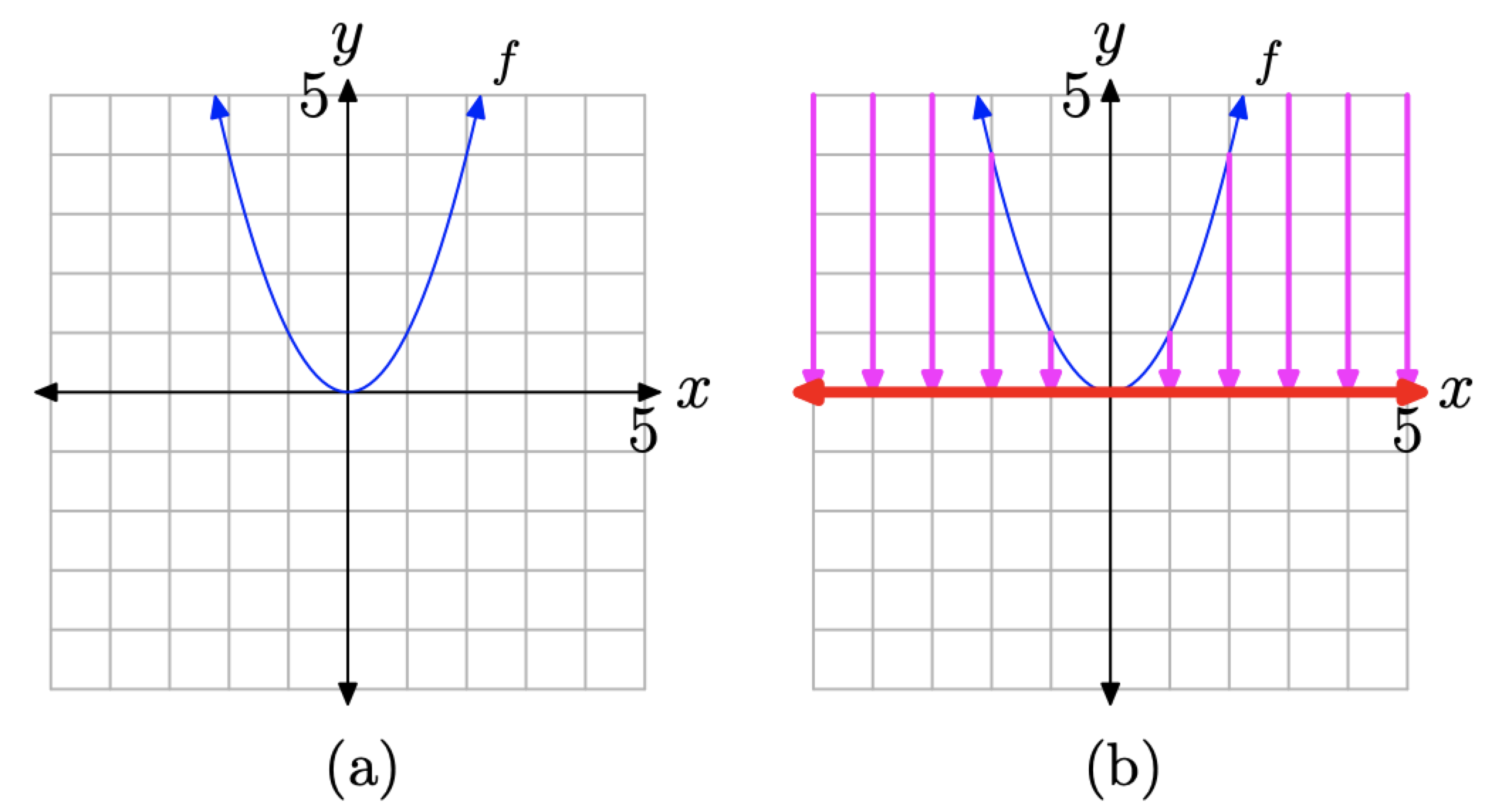
Figura\(\PageIndex{12}\). Determinar el dominio a partir de la gráfica de f.

Solución

Para determinar el dominio de f, debemos proyectar todos los puntos de la gráfica de f sobre el eje x. Esta proyección está indicada por la “sombra” roja (o estilo de línea más gruesa si está viendo esto en blanco y negro) que se muestra en el eje x en la Figura\(\PageIndex{12}\) (b). Hay que hacer dos puntos importantes sobre esta “sombra” o proyección.

1. La flecha al final de la mitad izquierda de la gráfica de f en la Figura\(\PageIndex{12}\) (a) indica que esta mitad de la gráfica de f se abre indefinidamente hacia la izquierda y hacia arriba. En consecuencia, cuando los puntos de la mitad izquierda de la gráfica de f se proyectan sobre el eje x, la “sombra” o proyección se extiende indefinidamente hacia la izquierda. Observe cómo los puntos de la gráfica que caen fuera de la ventana de visualización entran desde la esquina superior izquierda y proyectan “sombras” en el eje x.
2. La flecha al final de la mitad derecha de la gráfica de f en la Figura\(\PageIndex{12}\) (a) indica que esta mitad de la gráfica de f se abre indefinidamente a la derecha y hacia arriba. En consecuencia, cuando los puntos de esta mitad de la gráfica de f se proyectan sobre el eje x, la “sombra” o proyección se extiende indefinidamente hacia la derecha.

En consecuencia, todo el eje x yace en “sombra”, haciendo que el dominio de f sea

\[\text { Domain of } f=(-\infty, \infty)=\{x : x \in \mathbb{R}\}\]

Para determinar el rango de f, debemos proyectar todos los puntos de la gráfica de f sobre el eje y. Esta proyección está indicada por la “sombra” roja (o línea más gruesa si está viendo esto en blanco y negro) que se muestra en el eje y en la Figura\(\PageIndex{13}\) (b). Hay que hacer dos puntos importantes sobre esta “sombra” o proyección.

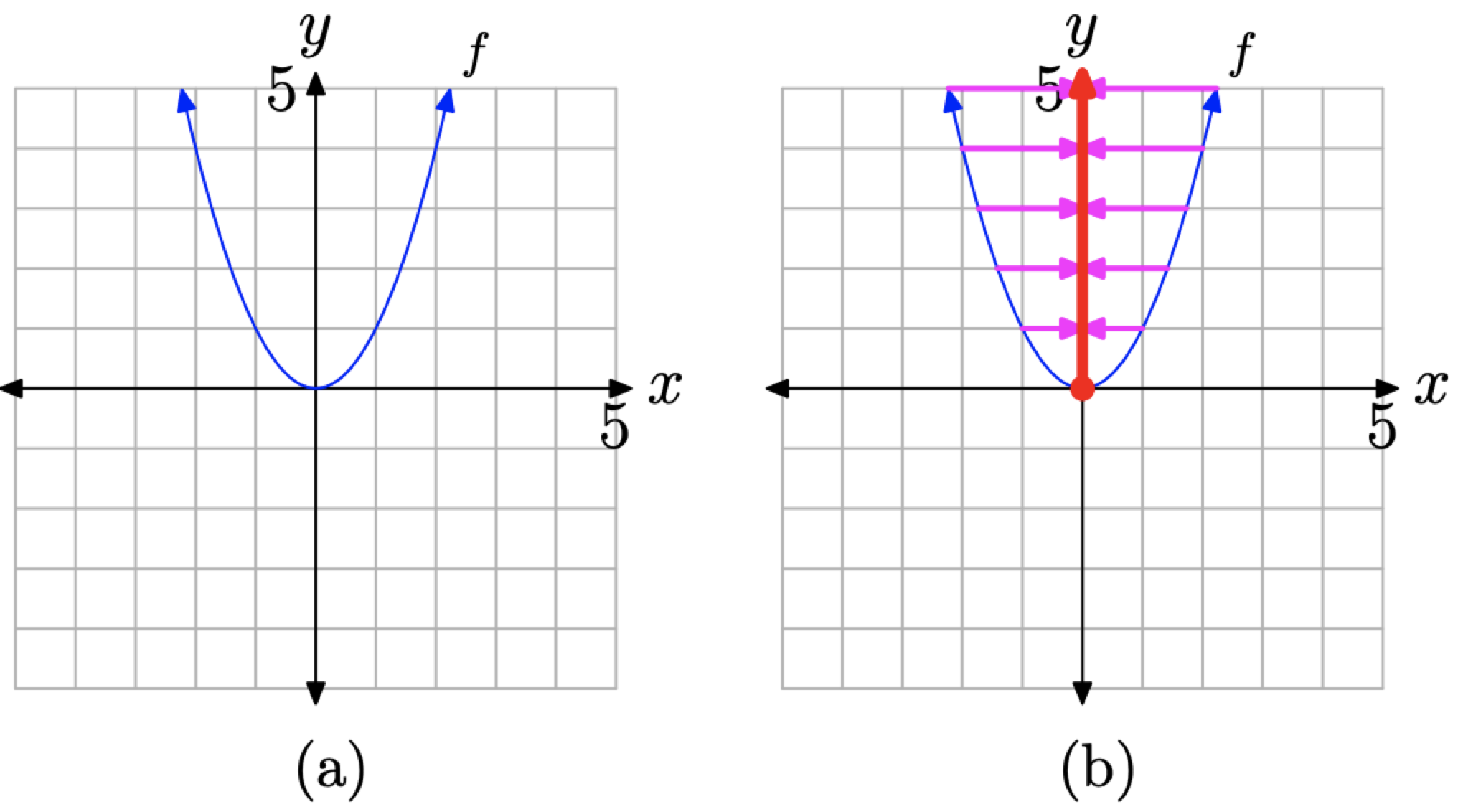
Figura\(\PageIndex{13}\). Determinar el rango a partir de la gráfica de f.

1. La gráfica de f pasa por el origen (el punto (0, 0)). Este es el punto más bajo de la gráfica y, por lo tanto, su sombra es el punto final en el extremo inferior de la región sombreada en el eje y.
2. Las flechas al final de cada mitad de la gráfica de f indican que la gráfica se abre hacia arriba indefinidamente. De ahí que cuando los puntos de la gráfica de f se proyectan sobre el eje y, la “sombra” o proyección se extiende hacia arriba indefinidamente. Esto se indica con una flecha en el extremo superior de la “sombra” en el eje y.

En consecuencia, todos los puntos en el eje y por encima e incluyendo el punto en el origen “se encuentran en la sombra”. Por lo tanto, el rango de f es

\[\text { Range of } f=[0, \infty)=\{y : y \geq 0\}\]

Uso de una calculadora gráfica para determinar el dominio y el rango

Hemos aprendido a encontrar el dominio y el rango de una función mirando su gráfica. Por lo tanto, si definimos una función por medio de una expresión\(f(x)=\sqrt{4-x}\), tal como, entonces deberíamos poder capturar el dominio y rango de f a partir de su gráfica, siempre y cuando, por supuesto, podamos dibujar la gráfica de f. Encontraremos que la calculadora gráfica será una herramienta útil para este ejercicio.

Ejemplo\(\PageIndex{6}\)

Utilice el generador de conjuntos y la notación de intervalos para describir el dominio y el rango de la función definida por la regla

\[f(x)=\sqrt{4-x}\]

Solución

Cargue la expresión definiendo f en el menú Y=, como se muestra en la Figura\(\PageIndex{14}\) (a). Seleccione 6:ZStandard en el menú ZOOM para producir la gráfica de f que se muestra en la Figura\(\PageIndex{14}\) (b).

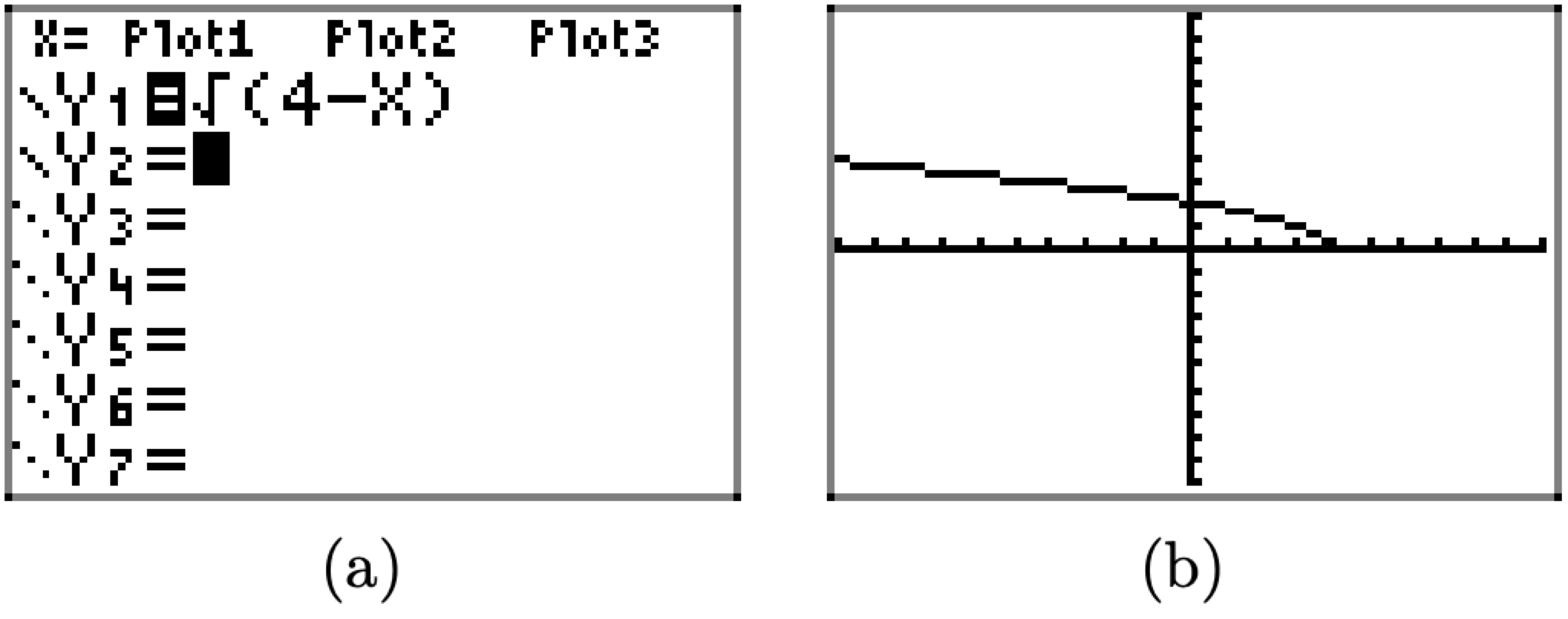
Figura\(\PageIndex{14}\). Dibujando la gráfica de\(f(x)=\sqrt{4-x}\).

Copia la imagen de la Figura\(\PageIndex{14}\) (b) en una hoja de papel cuadriculado. Etiquete y escale cada eje con los parámetros WINDOW xmin, xmax, ymin e ymax, como se muestra en la Figura\(\PageIndex{15}\) (a).

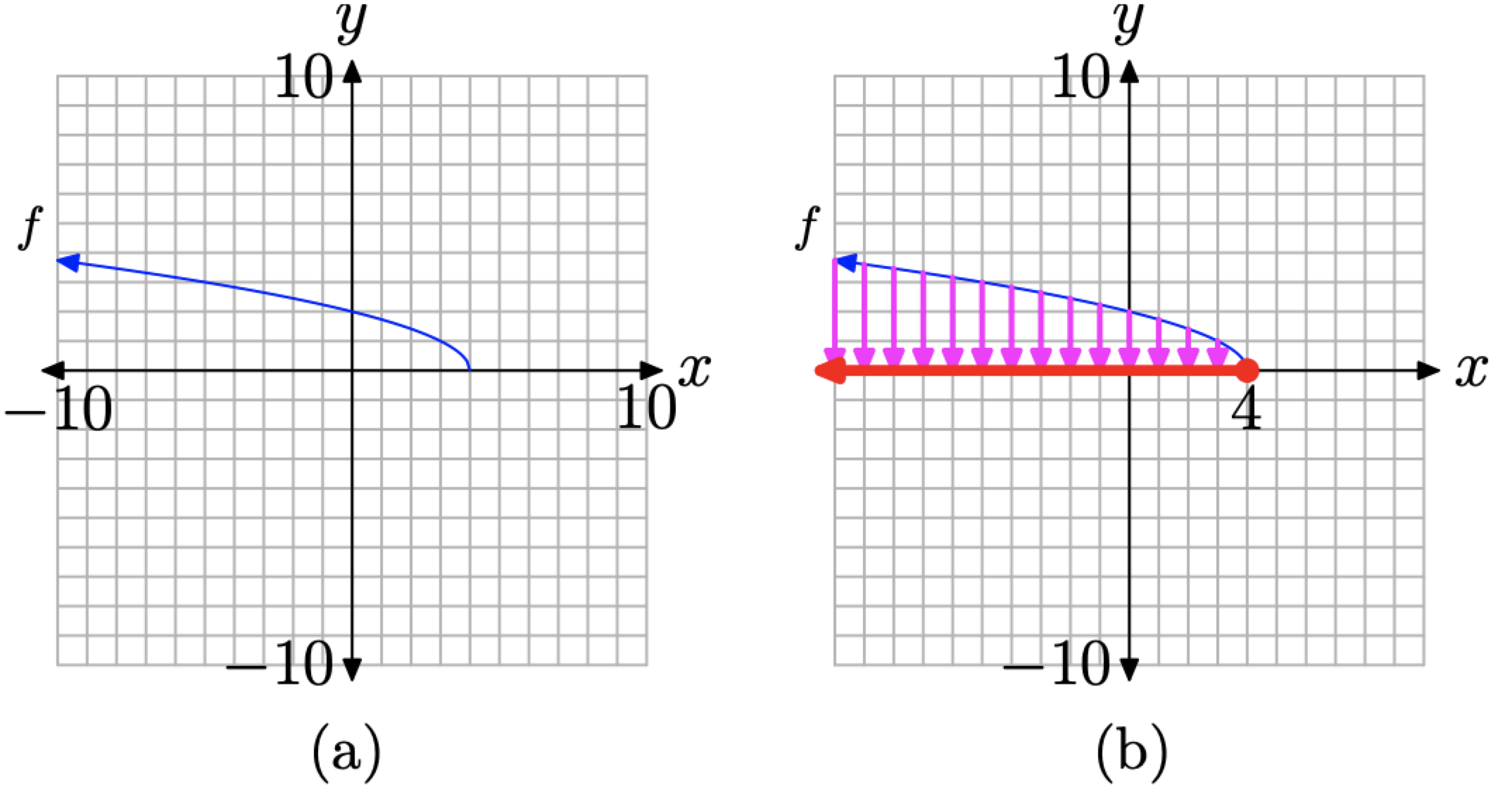
Figura\(\PageIndex{15}\). Capturando el dominio de\(f(x)=\sqrt{4-x}\) desde su gráfica.

A continuación, proyecte cada punto de la gráfica de f sobre el eje x, como se muestra en la Figura\(\PageIndex{15}\) (b). Tenga en cuenta que hemos hecho dos suposiciones sobre la gráfica de f.

1. En el extremo izquierdo de la gráfica en las Figuras\(\PageIndex{14}\) (b) y\(\PageIndex{15}\) (b), suponemos que la gráfica de f continúa hacia arriba y hacia la izquierda indefinidamente. De ahí que la “sombra” o proyección sobre el eje x se moverá indefinidamente hacia la izquierda. Esto se indica uniendo una punta de flecha al extremo izquierdo de la región que “yace en sombra” en el eje x, como se muestra en la Figura\(\PageIndex{15}\) (b).
2. También asumimos que el extremo derecho de la gráfica termina en el punto\((4, 0)\). Esto explica el “punto relleno” cuando este punto en la gráfica de f se proyecta sobre el eje x.

Tenga en cuenta que la “sombra” o proyección sobre el eje x en la Figura\(\PageIndex{15}\) (b) incluye todos los valores de x menores o iguales a 4. Así, el dominio de f es\[\text { Domain of } f=(-\infty, 4]=\{x : x \leq 4\}\]

Podemos intuir este resultado considerando la expresión que define f. es decir, considerar la regla o definición

\[f(x)=\sqrt{4-x}\]

Recordemos que anteriormente definimos el dominio de f como el conjunto de valores x “permisibles”. En este caso, es imposible tomar la raíz cuadrada de un número negativo, por lo que debemos tener cuidado seleccionando los valores x que usamos en esta regla. Tenga en cuenta que\(x = 4\) es permisible, como

\[f(0)=\sqrt{4-4}=\sqrt{0}=0\]

Sin embargo, en esta regla no se pueden usar números mayores a 4. Por ejemplo, considera lo que sucede cuando intentamos usar\(x = 5\).

\[f(x)=\sqrt{4-5}=\sqrt{-1}\]

Dejaremos que nuestros lectores prueben otros valores de x que sean menores a 4. También producirán respuestas reales cuando se introduzcan en la regla\(f(x)=\sqrt{4-x}\). Tenga en cuenta que esto también verifica nuestra conjetura anterior de que la “sombra” o proyección mostrada en la Figura\(\PageIndex{15}\) (b) continúa indefinidamente hacia la izquierda.

En lugar de “adivinar y verificar”, podemos acelerar el análisis del dominio de\(f(x)=\sqrt{4-x}\) al señalar que la expresión bajo el radical no debe ser un número negativo. Por lo tanto,\(4 − x\) debe ser mayor o igual a cero. Este argumento produce una desigualdad que se resuelve fácilmente para x.

\[\begin{aligned} 4-x & \geq 0 \\-x & \geq-4 \\ x & \leq 4 \end{aligned}\]

Este último resultado verifica que el dominio de f es todos los valores de x que son menores o iguales a 4, lo que está en total acuerdo con la “sombra” o proyección sobre el eje x que se muestra en la Figura\(\PageIndex{15}\) (b).

Para determinar el rango de f, debemos proyectar cada punto de la gráfica de f sobre el eje y, como se muestra en la Figura\(\PageIndex{16}\) (b).

Nuevamente, hacemos dos suposiciones sobre la gráfica de f.

1. En el extremo izquierdo de la gráfica de\(f(x)=\sqrt{4-x}\) en las Figuras\(\PageIndex{14}\) (b) y\(\PageIndex{16}\) (b), suponemos que la gráfica de f continúa hacia arriba y hacia la izquierda indefinidamente. Así, cuando los puntos de la gráfica de f se proyectan sobre el eje y, habrá proyecciones provenientes de la parte superior izquierda de puntos en la gráfica de f que no son visibles en la ventana de visualización seleccionada en la Figura\(\PageIndex{14}\) (b). De ahí que la “sombra” o proyección sobre el eje y que se muestra en la Figura\(\PageIndex{16}\) (b) continúe hacia arriba indefinidamente. Esto se indica con una punta de flecha en el extremo superior de la “sombra” en el eje y en la Figura\(\PageIndex{16}\) (b).

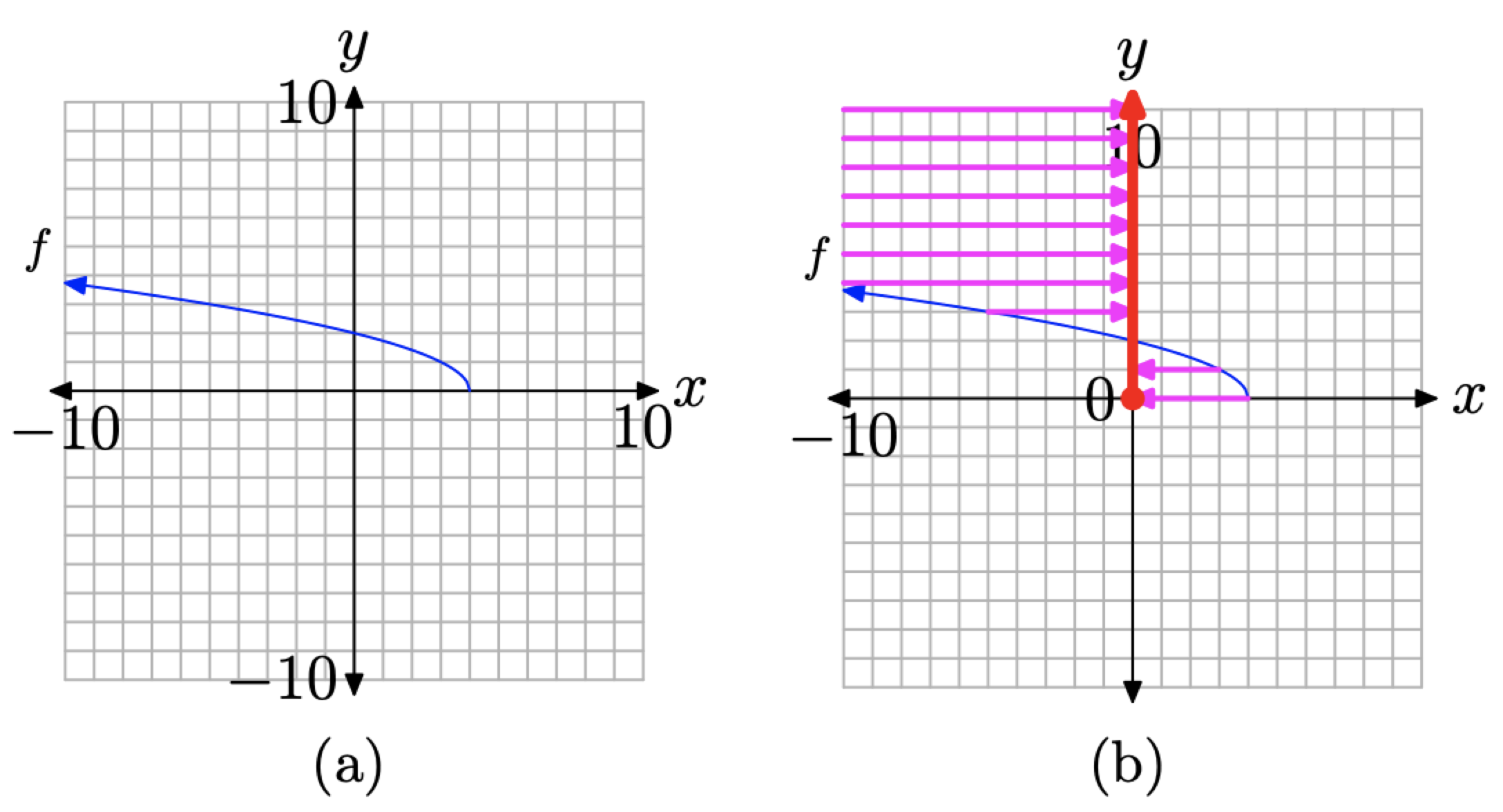
Figura\(\PageIndex{16}\). Determinar el rango de\(f(x)=\sqrt{4-x}\) desde su gráfica.

2. Nuevamente, asumimos que el extremo derecho de la gráfica de f termina en el punto\((4, 0)\). La proyección de este punto sobre el eje y produce el punto final “relleno” en el origen mostrado en la Figura\(\PageIndex{16}\) (b).

Tenga en cuenta que la “sombra” o proyección sobre el eje y en la Figura\(\PageIndex{16}\) (b) incluye todos los valores de y que son mayores o iguales a cero. Por lo tanto,

\[\text { Range of } f=[0, \infty)=\{y : y \geq 0\}\]