2.4: Resolver ecuaciones y desigualdades mediante gráficos

Nuestro énfasis en el capítulo ha estado en las funciones y la interpretación de sus gráficas. En esta sección, continuamos en esa línea y volvemos nuestra exploración a la solución de ecuaciones y desigualdades mediante la gráfica. Las ecuaciones tendrán la forma\(f(x) = g(x)\), y las desigualdades tendrán forma\(f(x) < g(x)\) y/o\(f(x) > g(x)\).

Quizás te preguntes por qué no hemos mencionado las desigualdades que tienen la forma\(f(x) \leq g(x)\) y\(f(x) \geq g(x)\). El motivo de esta omisión es el hecho de que la solución de la desigualdad\(f(x) \leq g(x)\) es simplemente la unión de las soluciones de\(f(x) = g(x)\) y\(f(x) < g(x)\). Después de todo,\(\leq\) se pronuncia “menor que o igual”. Comentarios similares están en orden para la desigualdad\(f(x) \geq g(x)\).

Comenzaremos comparando los valores de función de dos funciones f y g a diversos valores de x en sus dominios.

Comparación de funciones

Supongamos que evaluamos dos funciones f y g a un valor particular de x. Uno de los tres resultados es posible. O bien

\[f(x)=g(x), \quad \text { or } \quad f(x)>g(x), \quad \text { or } \quad f(x)<g(x)\]

Es bastante sencillo comparar dos valores de función a un valor particular si se dan reglas para cada función.

Ejemplo\(\PageIndex{1}\)

Dado\(f(x)=x^{2}\) y\(g(x) = 2x+3\), compare las funciones en x = −2, 0 y 3.

Solución

Los cálculos simples revelan las relaciones.

• A x = −2,\[f(-2)=(-2)^{2}=4 \quad \text { and } \quad g(-2)=2(-2)+3=-1\] tan claramente,\(f(−2) > g(−2)\).
• A x = 0,\[f(0)=(0)^{2}=0 \quad \text { and } \quad g(0)=2(0)+3=3\] tan claramente,\(f(0) < g(0)\).
• Por último, a x = 3,\[f(3)=(3)^{2}=9 \quad \text { and } \quad g(3)=2(3)+3=9\] tan claramente,\(f(3) = g(3)\).

También podemos comparar valores de función a un valor particular de x examinando las gráficas de las funciones. Por ejemplo, considere las gráficas de dos funciones f y g en la Figura\(\PageIndex{1}\).

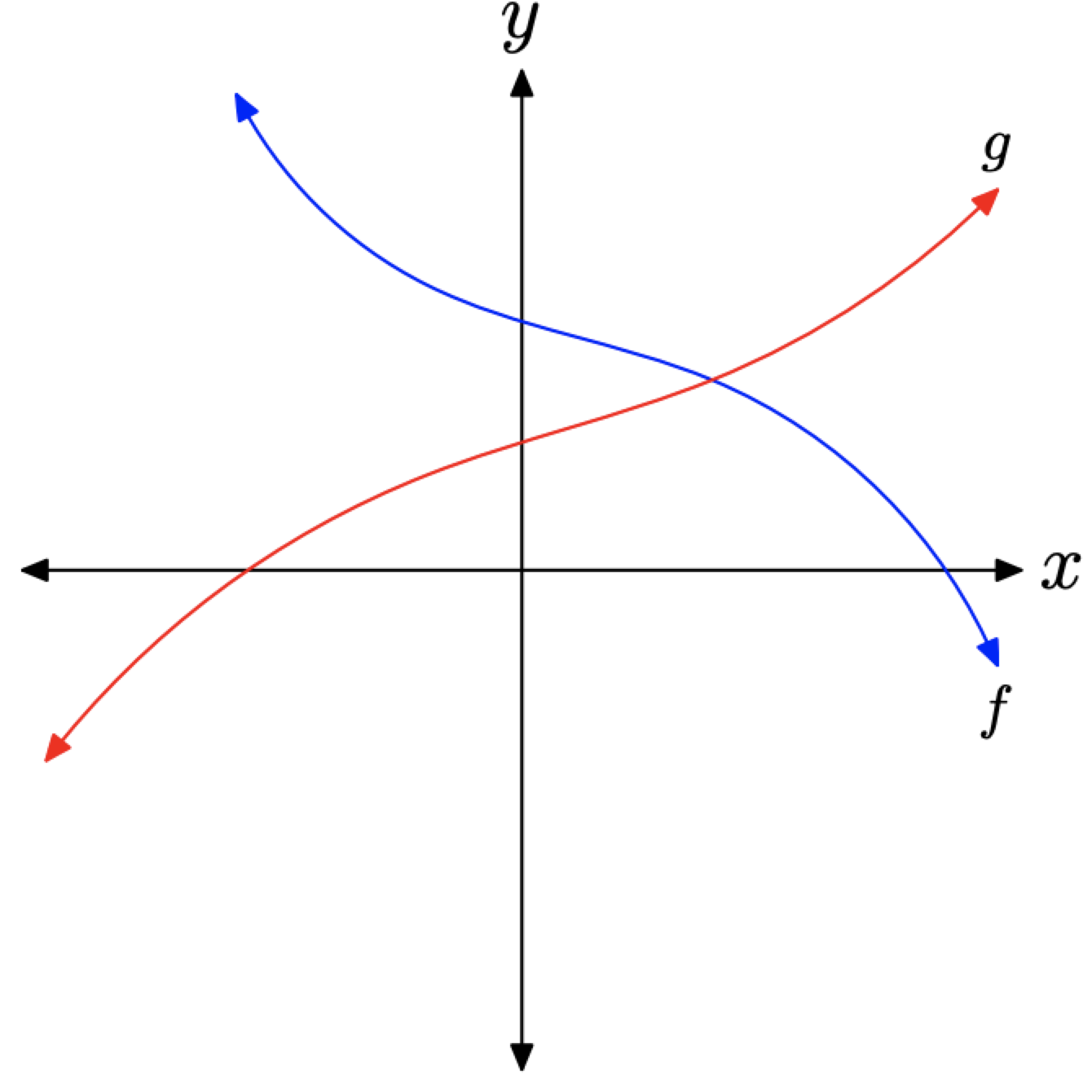
Figura\(\PageIndex{1}\)

A continuación, supongamos que dibujamos una línea vertical discontinua a través del punto de intersección de las gráficas de f y g, luego seleccionamos un valor de x que se encuentra a la izquierda de la línea vertical discontinua, como se muestra en la Figura\(\PageIndex{2}\) (a). Debido a que la gráfica de f se encuentra por encima de la gráfica de g para todos los valores de x que se encuentran a la izquierda de la línea vertical discontinua, será el caso que\(f(x) > g(x)\) para todos esos x (ver Figura\(\PageIndex{2}\) (a)).

Por otro lado, la gráfica de f se encuentra debajo de la gráfica de g para todos los valores de x que se encuentran a la derecha de la línea vertical discontinua. De ahí que para todos esos x, será el caso que\(f(x) < g(x)\) (ver Figura\(\PageIndex{2}\) (b)).

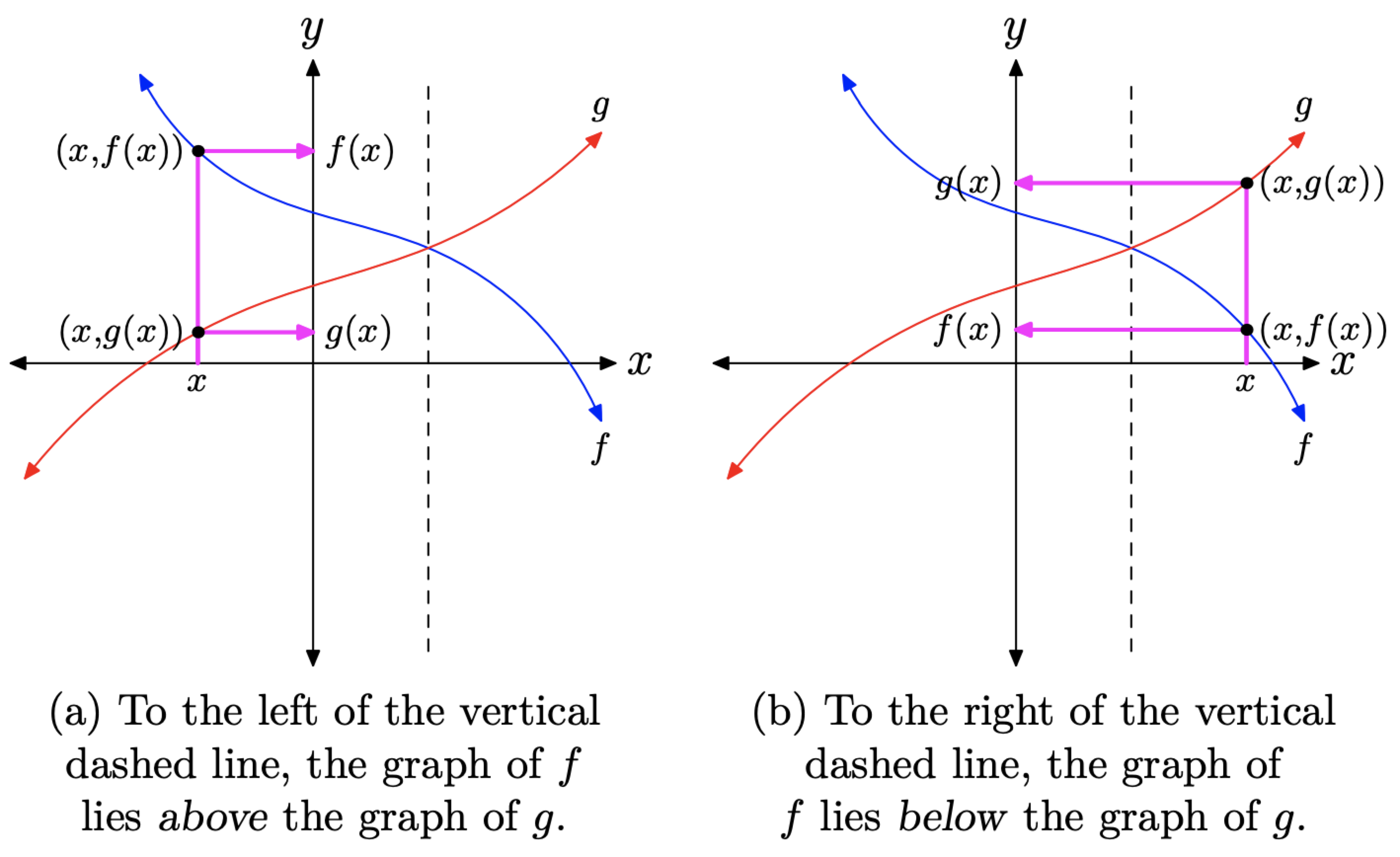
Figura\(\PageIndex{2}\). Comparando f y g.

Por último, si seleccionamos el valor x del punto de intersección de las gráficas de f y g, entonces para este valor de x, es el caso de que f (x) y g (x) sean iguales; es decir,\(f(x) = g(x)\) (ver Figura\(\PageIndex{3}\)).

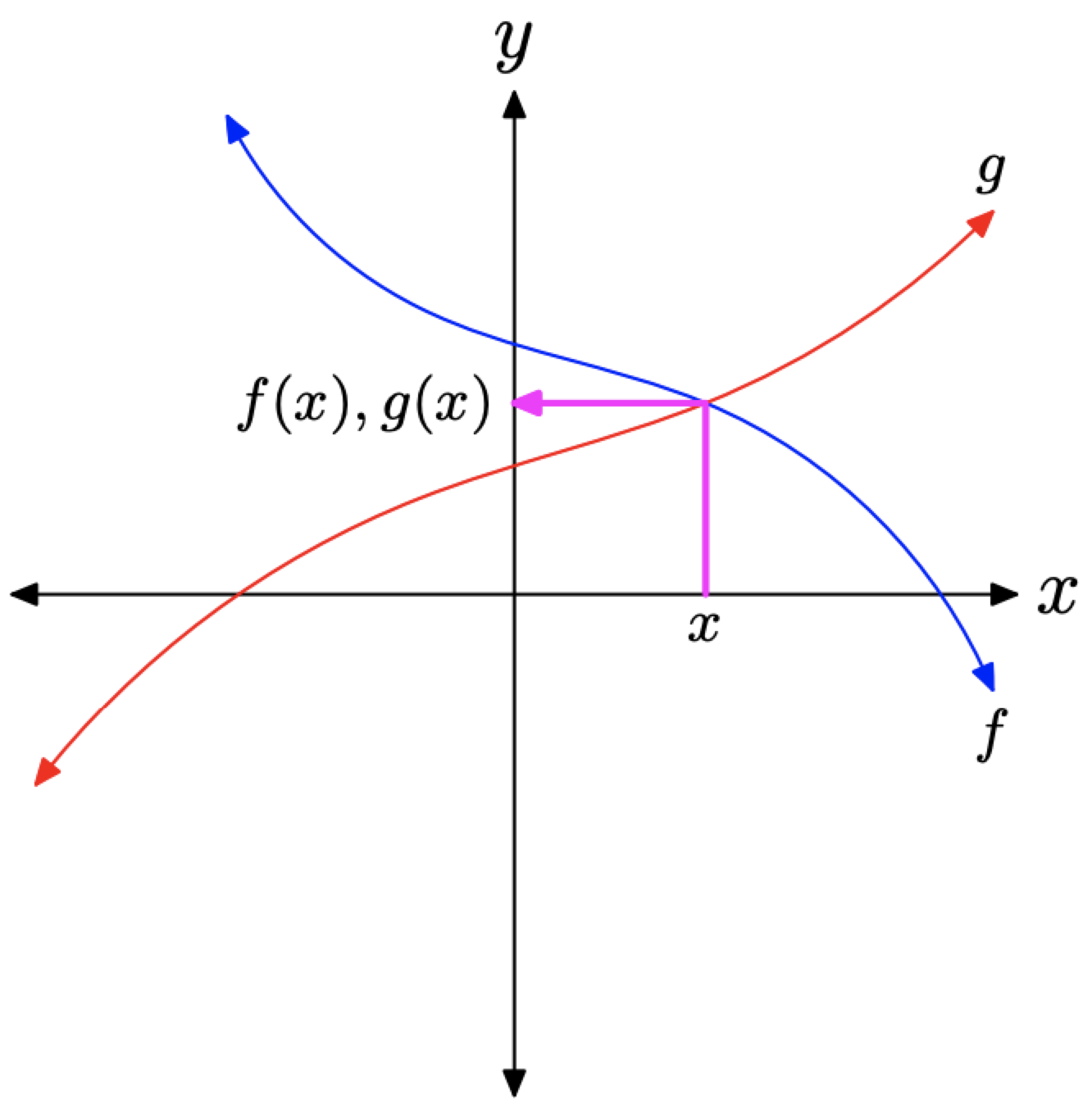
Figura\(\PageIndex{3}\). Los valores de función f (x) y g (x) son iguales donde se cruzan las gráficas de f y g.

Resumamos nuestros hallazgos.

Resumen

1. La solución de la ecuación f (x) = g (x) es el conjunto de todos x para los que se cruzan las gráficas de f y g.
2. La solución de la desigualdad f (x) < g (x) es el conjunto de todos x para el que la gráfica de f se encuentra debajo de la gráfica de g.
3. La solución de la desigualdad f (x) > g (x) es el conjunto de todos x para el que la gráfica de f se encuentra por encima de la gráfica de g.

Veamos un ejemplo.

Ejemplo\(\PageIndex{2}\)

Dadas las gráficas de f y g en la Figura\(\PageIndex{4}\) (a), utilice tanto el set-builder como la notación de intervalo para describir la solución de la desigualdad f (x) < g (x). Después, encuentra las soluciones de la desigualdad f (x) > g (x) y la ecuación f (x) = g (x) de manera similar.

Solución

Para encontrar la solución de f (x) < g (x), debemos ubicar donde se encuentra la gráfica de f debajo de la gráfica de g. Dibujamos una línea vertical discontinua a través del punto de intersección de las gráficas de f y g (ver Figura\(\PageIndex{4}\) (b)), luego anotar que la gráfica de f se encuentra debajo de la gráfica de g a la izquierda de esta línea discontinua. En consecuencia, la solución de la desigualdad f (x) < g (x) es la colección de todas las x que se encuentran a la izquierda de la línea discontinua. Este conjunto está sombreado en rojo (o en un estilo de línea más grueso si se ve en blanco y negro) en el eje x en la Figura\(\PageIndex{4}\) (b).

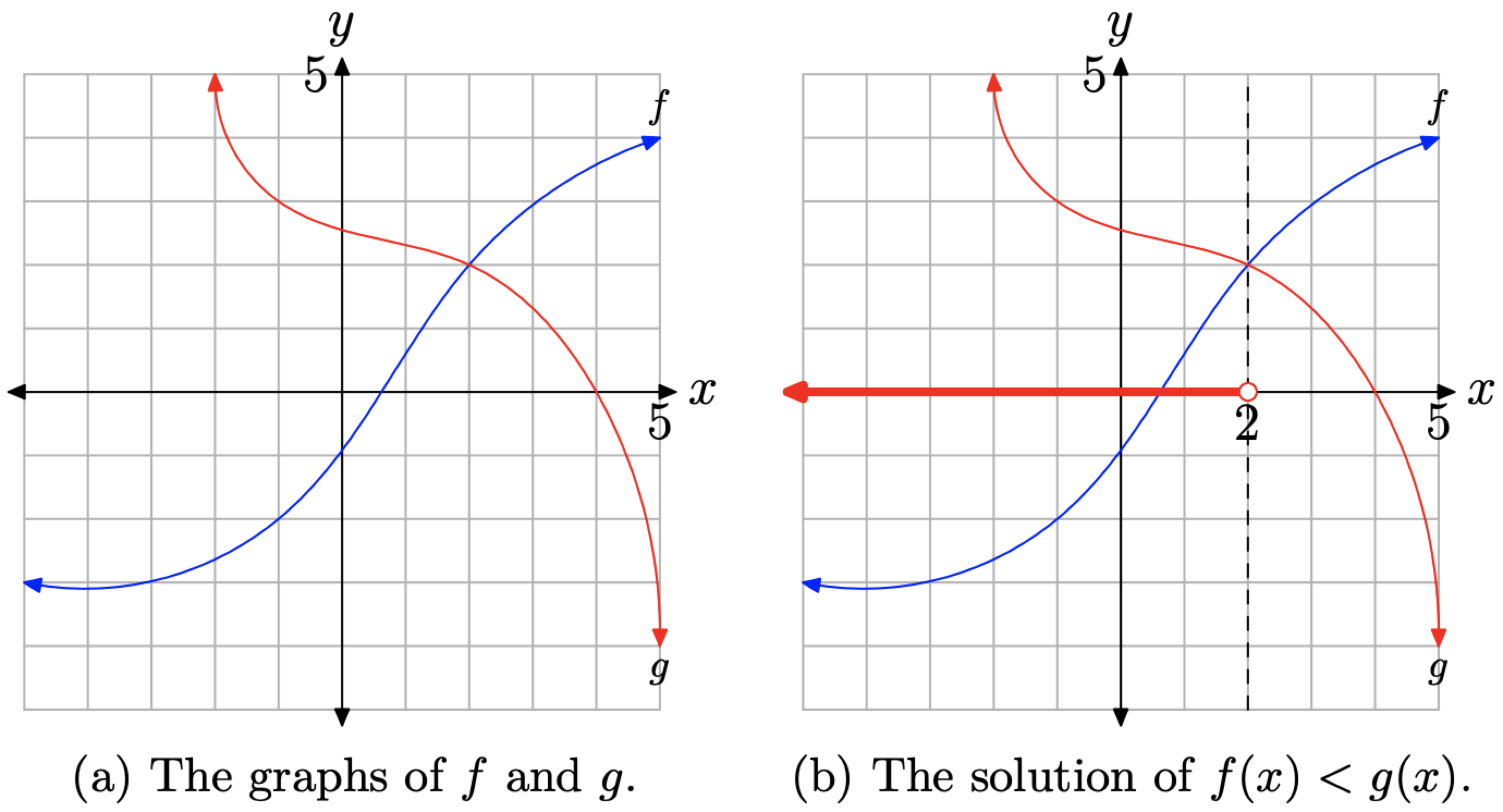
Figura\(\PageIndex{4}\). Comparando f y g.

Tenga en cuenta que los puntos sombreados en el eje x tienen valores x menores que 2. Por lo tanto, la solución de f (x) < g (x) es\[(-\infty, 2)=\{x : x<2\}\]

De igual manera, la solución de f (x) > g (x) se encuentra anotando donde la gráfica de f se encuentra por encima de la gráfica de g y sombreando los valores x correspondientes en el eje x (ver Figura\(\PageIndex{5}\) (a)). La solución de f (x) > g (x) es\((2, \infty)\), o alternativamente,\(\{x : x>2\}\).

Para encontrar la solución de f (x) = g (x), anote donde la gráfica de f se cruza con la gráfica de g, luego sombrea el valor x de este punto de intersección en el eje x (ver Figura\(\PageIndex{5}\) (b)). Por lo tanto, la solución de f (x) = g (x) es\(\{x : x = 2\}\). Esto no es un intervalo, por lo que no es apropiado describir esta solución con notación de intervalo.

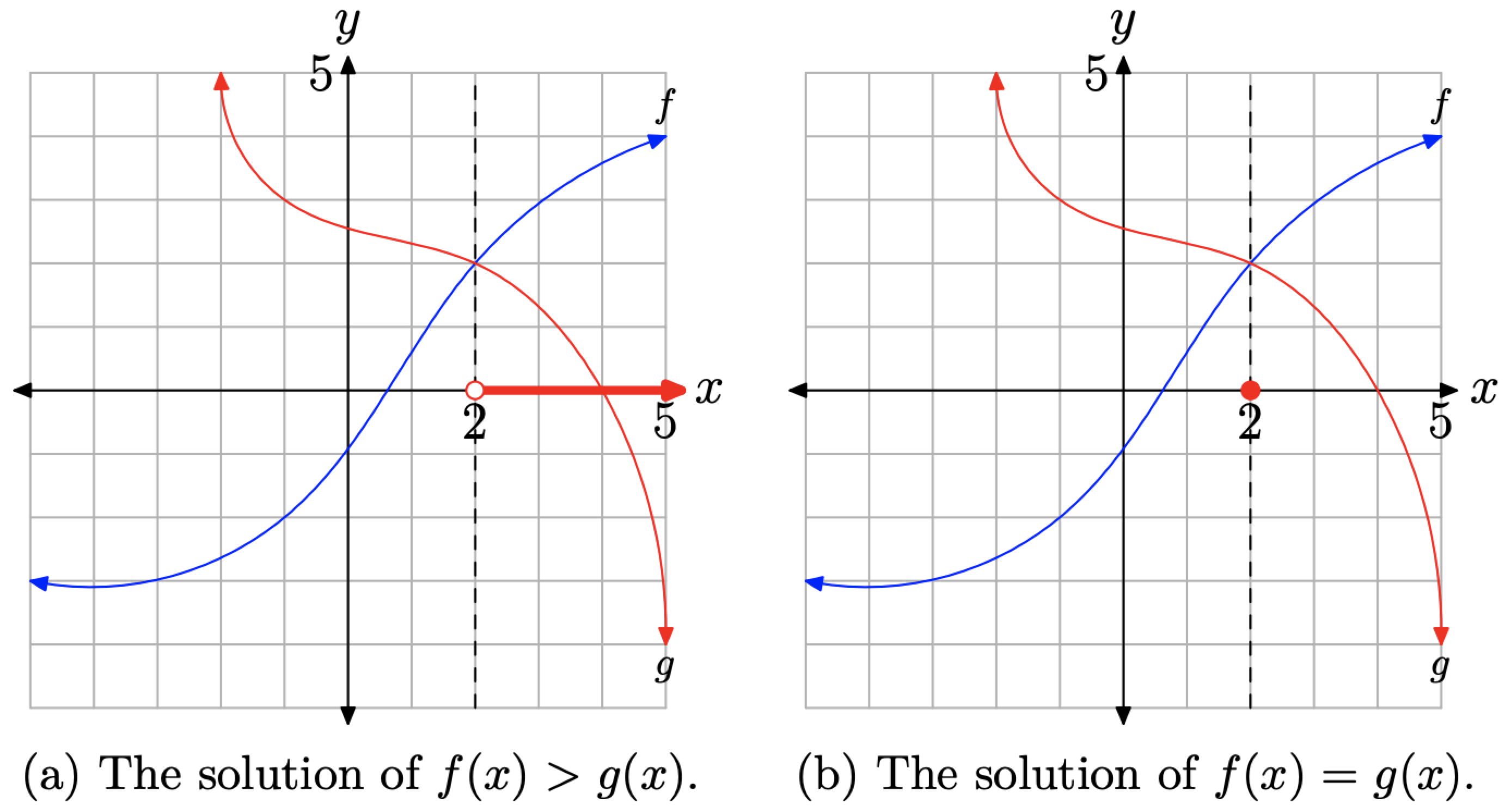
Figura\(\PageIndex{5}\). Otras comparaciones.

Veamos otro ejemplo.

Ejemplo\(\PageIndex{3}\)

Dadas las gráficas de f y g en la Figura\(\PageIndex{6}\) (a), utilice tanto el set-builder como la notación de intervalo para describir la solución de la desigualdad f (x) > g (x). Después, encuentra las soluciones de la desigualdad f (x) < g (x) y la ecuación f (x) = g (x) de manera similar.

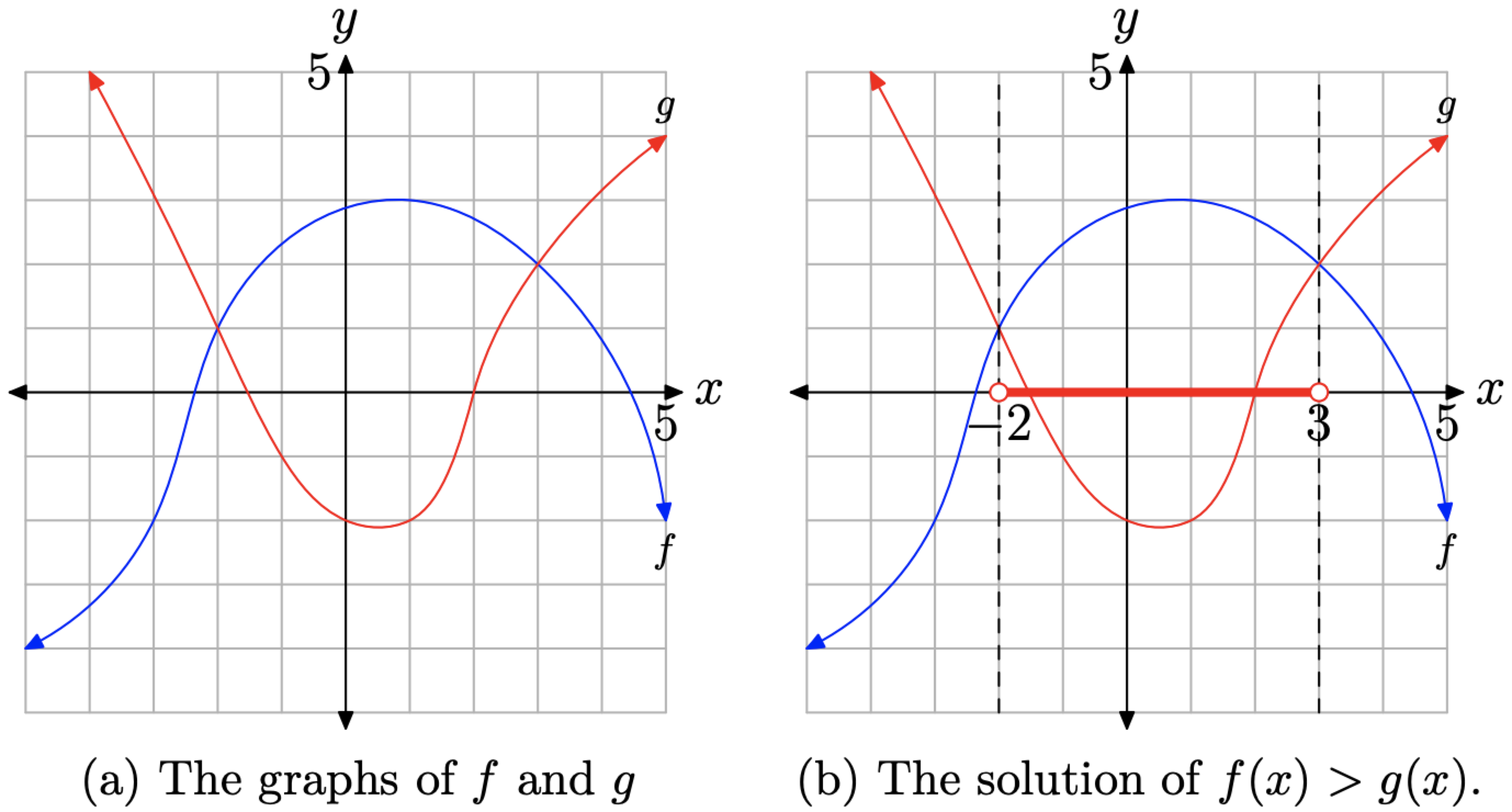
Figura\(\PageIndex{6}\). Comparando f y g.

Solución

Para determinar la solución de f (x) > g (x), debemos ubicar donde se encuentra la gráfica de f por encima de la gráfica de g. Dibujar líneas verticales discontinuas a través de los puntos de intersección de las gráficas de f y g (ver Figura\(\PageIndex{6}\) (b)), luego anotar que la gráfica de f se encuentra por encima de la gráfica de g entre las líneas verticales discontinuas recién dibujado. En consecuencia, la solución de la desigualdad f (x) > g (x) es la colección de todas las x que se encuentran entre las líneas verticales discontinuas. Hemos sombreado esta colección en el eje x en rojo (o con un estilo de línea más gruesa para quienes ven en blanco y negro) en la Figura\(\PageIndex{6}\) (b).

Tenga en cuenta que los puntos sombreados en el eje x en la Figura\(\PageIndex{6}\) (b) tienen valores x entre −2 y 3. En consecuencia, la solución de f (x) > g (x) es

\[(-2,3)=\{x :-2<x<3\}\]

De igual manera, la solución de f (x) < g (x) se encuentra anotando donde la gráfica de f se encuentra debajo de la gráfica de g y sombreando los valores x correspondientes en el eje x (ver Figura 7 (a)). Así, la solución de f (x) < g (x) es

\[(-\infty,-2) \cup(3, \infty)=\{x : x<-2 \text { or } x>3\}\]

Para encontrar la solución de f (x) = g (x), anote donde la gráfica de f se cruza con la gráfica de g, y sombrea el valor x de cada punto de intersección en el eje x (ver Figura\(\PageIndex{7}\) (b)). Por lo tanto, la solución de f (x) = g (x) es\(\{x : x=-2\) o\(x=3\}\). Debido a que este conjunto de soluciones no es un intervalo, sería inapropiado describirlo con notación de intervalo.

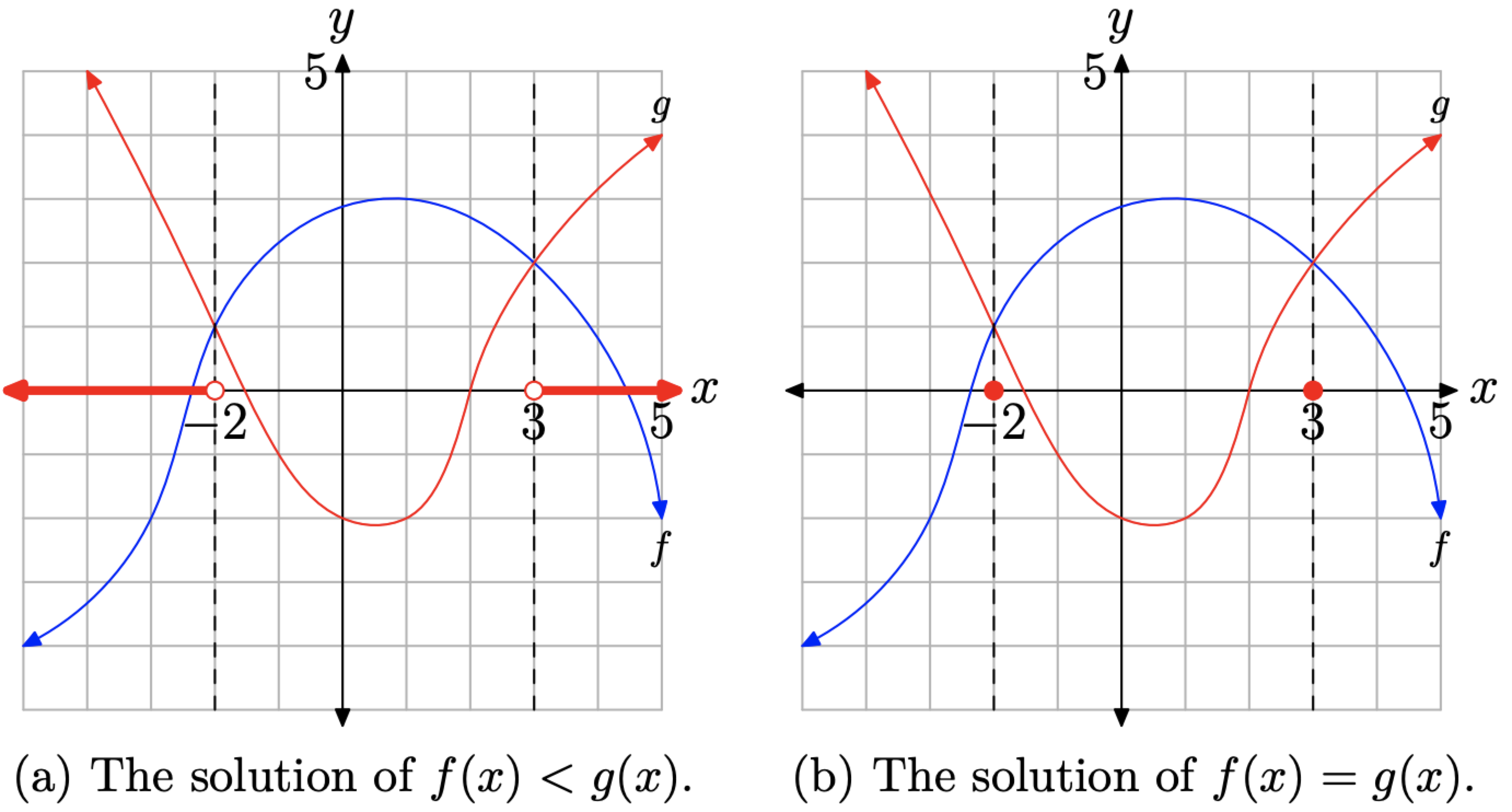
Figura\(\PageIndex{7}\). Otras comparaciones.

Resolviendo Ecuaciones y Desigualdades con la Calculadora Gráfica

Ahora sabemos que la solución de f (x) = g (x) es el conjunto de todos x para los que se cruzan las gráficas de f y g. Por lo tanto, la calculadora gráfica se convierte en una herramienta indispensable a la hora de resolver ecuaciones.

Ejemplo\(\PageIndex{4}\)

Usar una calculadora gráfica para resolver la ecuación

\[1.23 x-4.56=5.28-2.35 x \qquad (6)\]

Solución

Obsérvese que la ecuación (6) tiene la forma f (x) = g (x), donde

\[f(x)=1.23 x-4.56 \quad \text { and } \quad g(x)=5.28-2.35 x\]

Así, nuestro enfoque será dibujar las gráficas de f y g, luego encontrar el valor x del punto de intersección.

Primero, cargue f (x) = 1.23x − 4.56 en Y1 y g (x) = 5.28 − 2.35x en Y2 en el menú Y= de su calculadora gráfica (vea la Figura\(\PageIndex{8}\) (a)). Seleccione 6:ZStandard en el menú ZOOM para producir las gráficas de la Figura\(\PageIndex{8}\) (b).

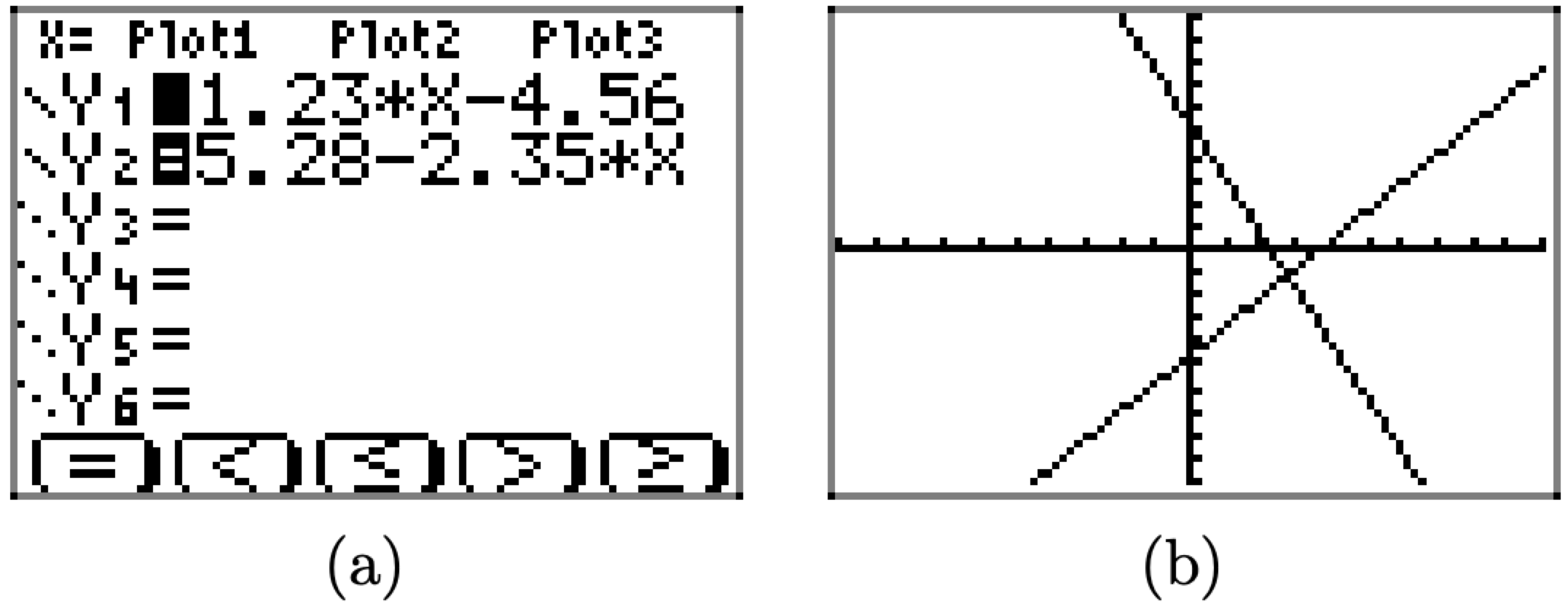
Figura\(\PageIndex{8}\). Dibujando las gráficas de f (x) = 1.23x−4.56 y g (x) = 5.28 − 2.35x.

La solución de la ecuación (6) es el valor x del punto de intersección de las gráficas de f y g en la Figura (\ PageIndex {8}\) (b). Utilizaremos la utilidad de intersección en el menú CALC en la calculadora gráfica para determinar las coordenadas del punto de intersección.

Procedemos de la siguiente manera:

• Seleccione 2do CALC (presione el 2do botón, seguido del botón TRACE), que abre el menú que se muestra en la Figura (\ PageIndex {9}\) (a).
• Seleccione 5:intersectar. La calculadora responde colocando el cursor sobre una de las gráficas, luego pregunta si quieres usar la curva seleccionada. Respondes afirmativamente presionando la tecla ENTRAR en la calculadora.
• La calculadora responde colocando el cursor en la segunda gráfica, luego pregunta si quieres usar la curva seleccionada. Responda afirmativamente presionando la tecla ENTER.
• La calculadora responde pidiéndote que hagas una conjetura. En este caso, solo hay dos gráficas en la calculadora, por lo que cualquier conjetura es apropiada.4 Simplemente presione la tecla ENTER para usar la posición actual del cursor como su suposición.

Figura\(\PageIndex{9}\). Uso de la utilidad intersect.

El resultado de esta secuencia de pasos se muestra en la Figura\(\PageIndex{10}\). Las coordenadas del punto de intersección son aproximadamente (2.7486034, −1.179218). El valor x de este punto de intersección es la solución de la ecuación (6). Es decir, la solución de\(1.23x − 4.56 = 5.28 − 2.35x\) es aproximadamente\(x \approx 2.7486034\).

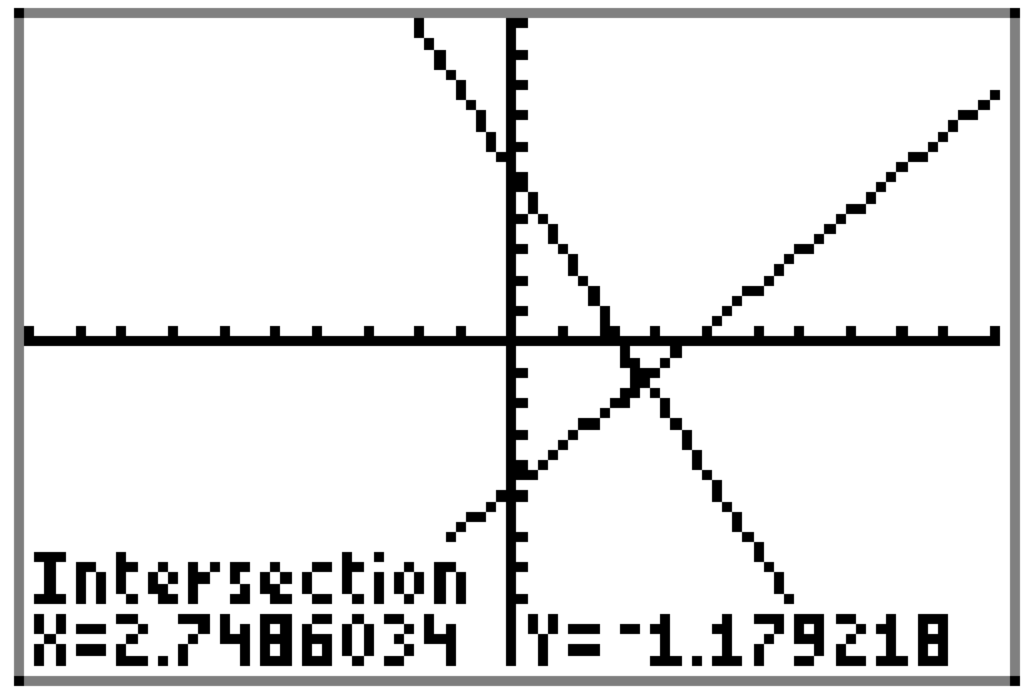
Figura\(\PageIndex{10}\). Las coordenadas del punto de intersección.

Resumen

Lineamientos.

Tendrás que discutir las expectativas con tu profesor, pero esperamos que nuestros alumnos resuman sus resultados de la siguiente manera.

1. Configure un sistema de coordenadas.6 Etiquete y escale cada eje con xmin, xmax, ymin e ymax.

2. Copie la imagen en su ventana de visualización en su sistema de coordenadas. Etiquete cada gráfica con su ecuación.

3. Dibuja una línea vertical discontinua a través del punto de intersección.

4. Sombra y etiqueta la solución de la ecuación en el eje x.

El resultado de seguir este estándar se muestra en la Figura\(\PageIndex{11}\).

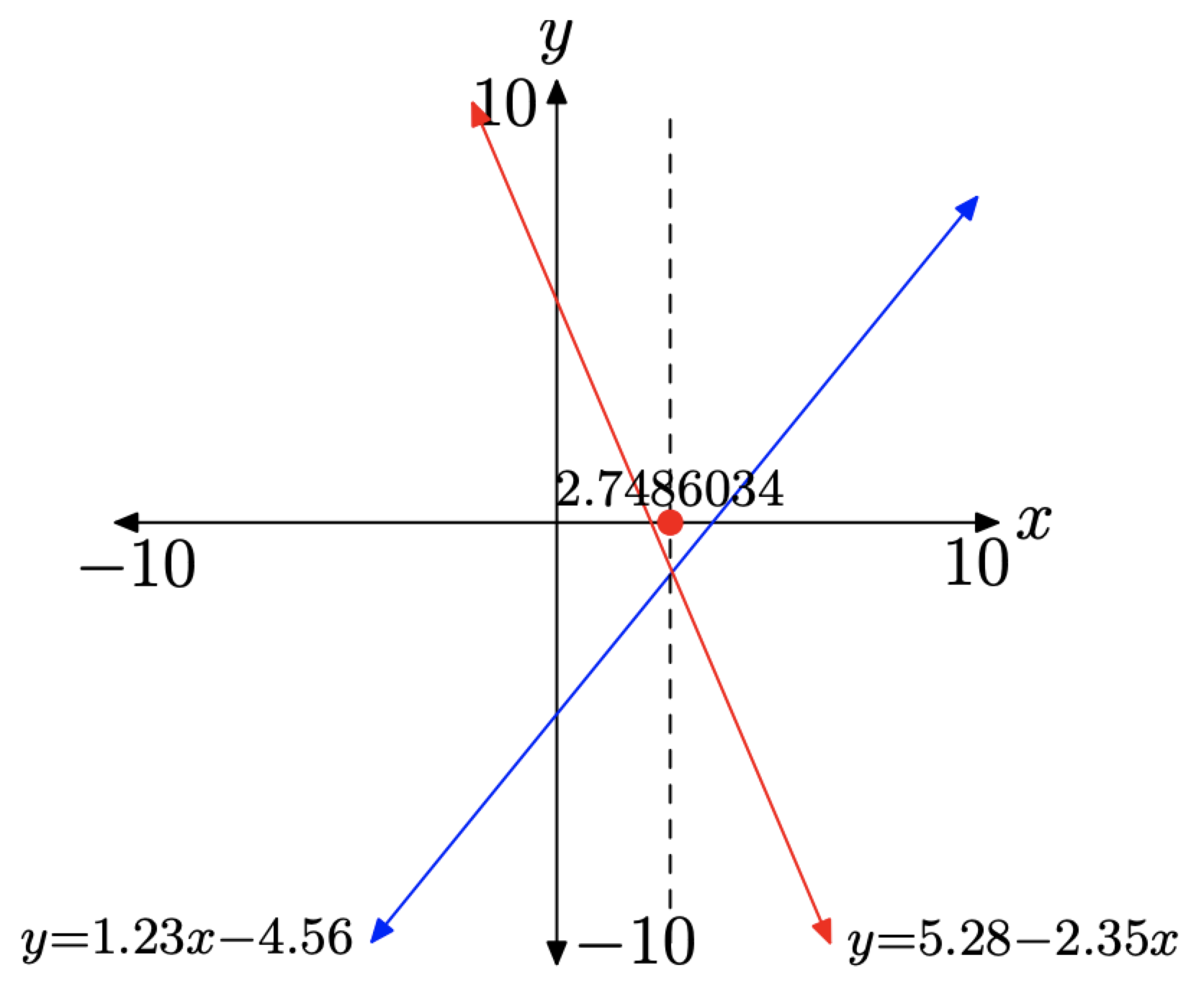
Figura\(\PageIndex{11}\). Resumiendo la solución de la ecuación (6).

Veamos otro ejemplo.

Ejemplo\(\PageIndex{5}\)

Usar el generador de conjuntos y la notación de intervalos para describir la solución de la desigualdad

\[0.85 x^{2}-3 \geq 1.23 x+1.25 \qquad (9)\]

Solución

Obsérvese que la desigualdad (9) tiene la forma\(f(x) \geq g(x)\), donde

\[f(x)=0.85 x^{2}-3 \quad \text { and } \quad g(x)=1.23 x+1.25\]

Cargue\(f(x)=0.85 x^{2}-3\) y\(g(x)=1.23 x+1.25\) en Y1 e Y2 en el menú Y=, respectivamente, como se muestra en la Figura\(\PageIndex{12}\) (a). Seleccione 6:ZStandard en el menú ZOOM para producir las gráficas que se muestran en la Figura\(\PageIndex{12}\) (b).

Para encontrar los puntos de intersección de las gráficas de f y g, seguimos la misma secuencia de pasos que hicimos en Ejemplo\(\PageIndex{4}\) hasta el punto donde la calculadora te pide hacer una conjetura (i.e., 2da CALC, 5:intersectar, Primera curva ENTRAR, Segunda curva ENTRAR). Porque hay dos puntos de intersección, cuando la calculadora te pide

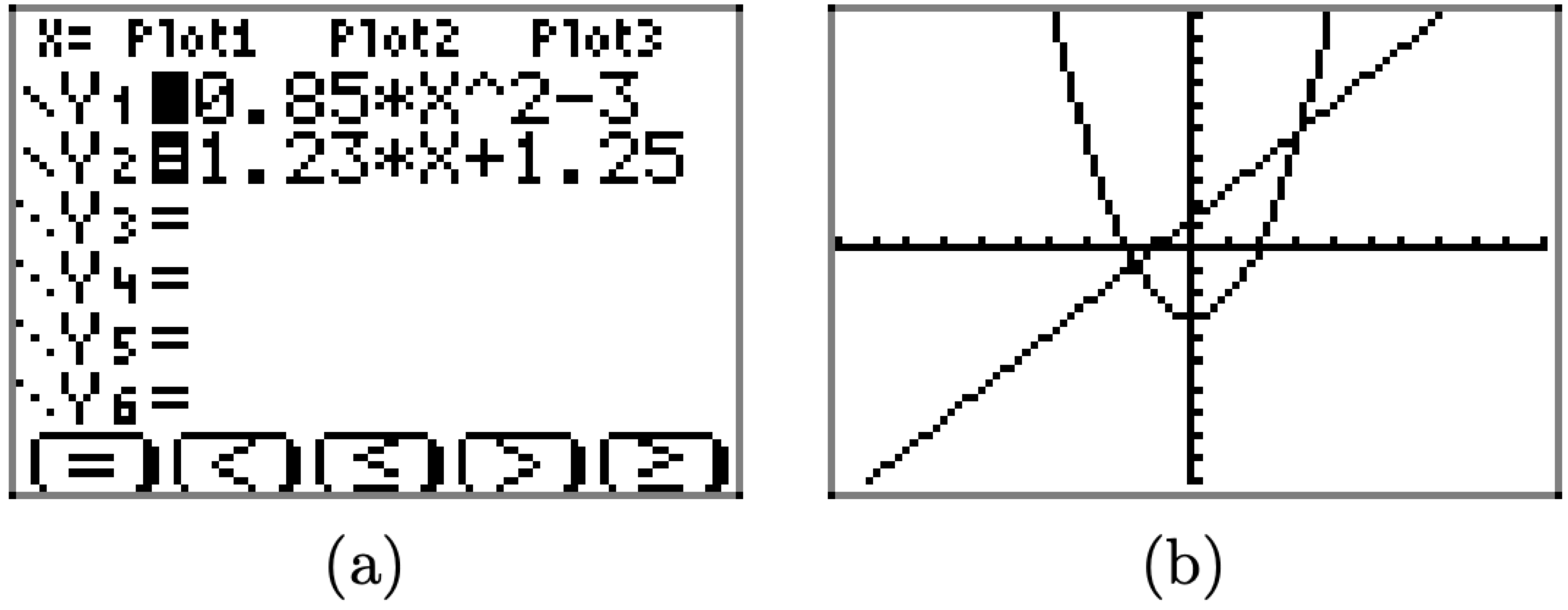
Figura\(\PageIndex{12}\). Las gráficas de\(f(x)=0.85 x^{2}-3\) y\(g(x) = 1.23x + 1.25\).

hacer una conjetura, debes mover tu cursor (con las teclas de flecha) para que esté más cerca del punto de intersección que deseas encontrar que del otro punto de intersección. Mediante esta técnica se producen los dos puntos de intersección que se encuentran en las Figuras\(\PageIndex{13}\) (a) y (b).

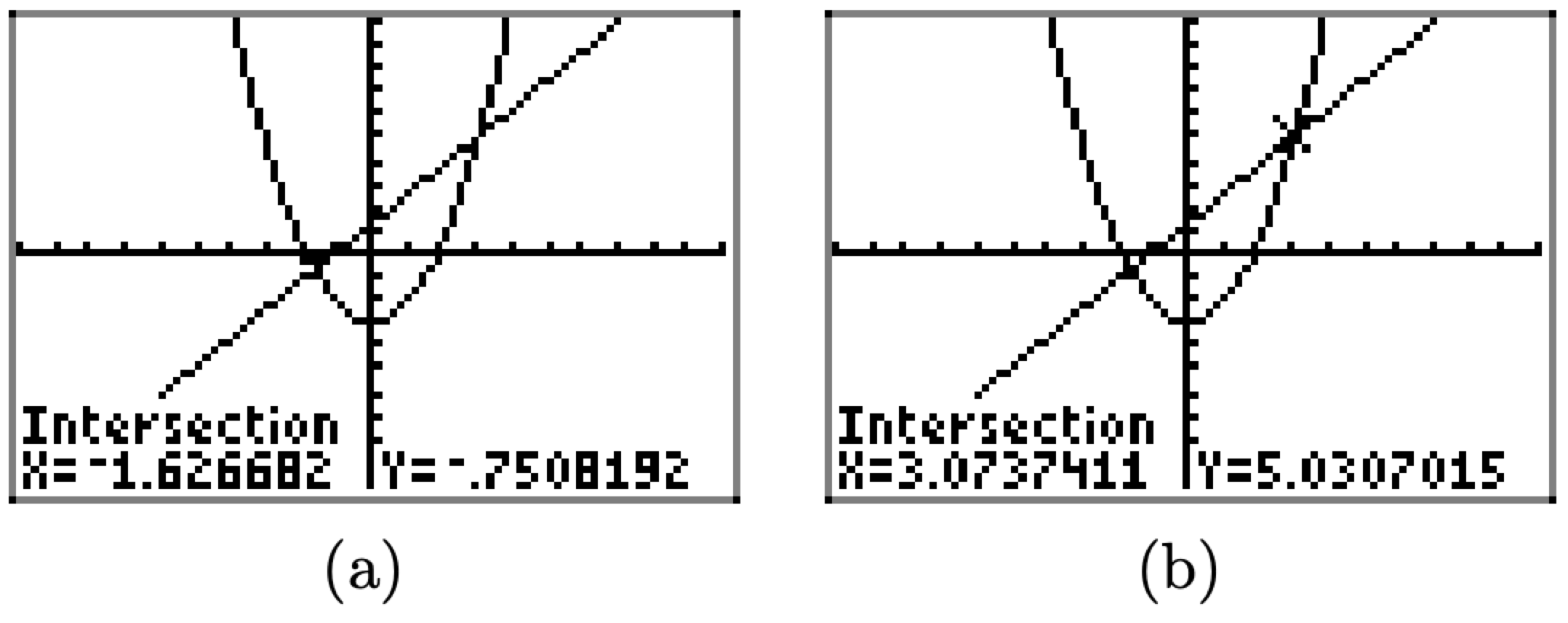
Figura\(\PageIndex{13}\). Los puntos de intersección de las gráficas de f y g.

Las coordenadas aproximadas del primer punto de intersección son (−1.626682, −0.7508192). El segundo punto de intersección tiene coordenadas aproximadas (3.0737411, 5.0307015).

Es importante recordar que cada vez que recoges tu calculadora, solo estás obteniendo una aproximación. Es posible que obtengas un resultado ligeramente diferente para los puntos de intersección. Por ejemplo, podría obtener (−1.626685, −0.7508187) para su punto de intersección. Con base en la posición del cursor cuando marcaste las curvas e hiciste tu suposición, puedes obtener aproximaciones ligeramente diferentes. Tenga en cuenta que esta segunda solución es casi la misma que la que encontramos, difiriendo sólo en los últimos decimales, y es perfectamente aceptable como respuesta.

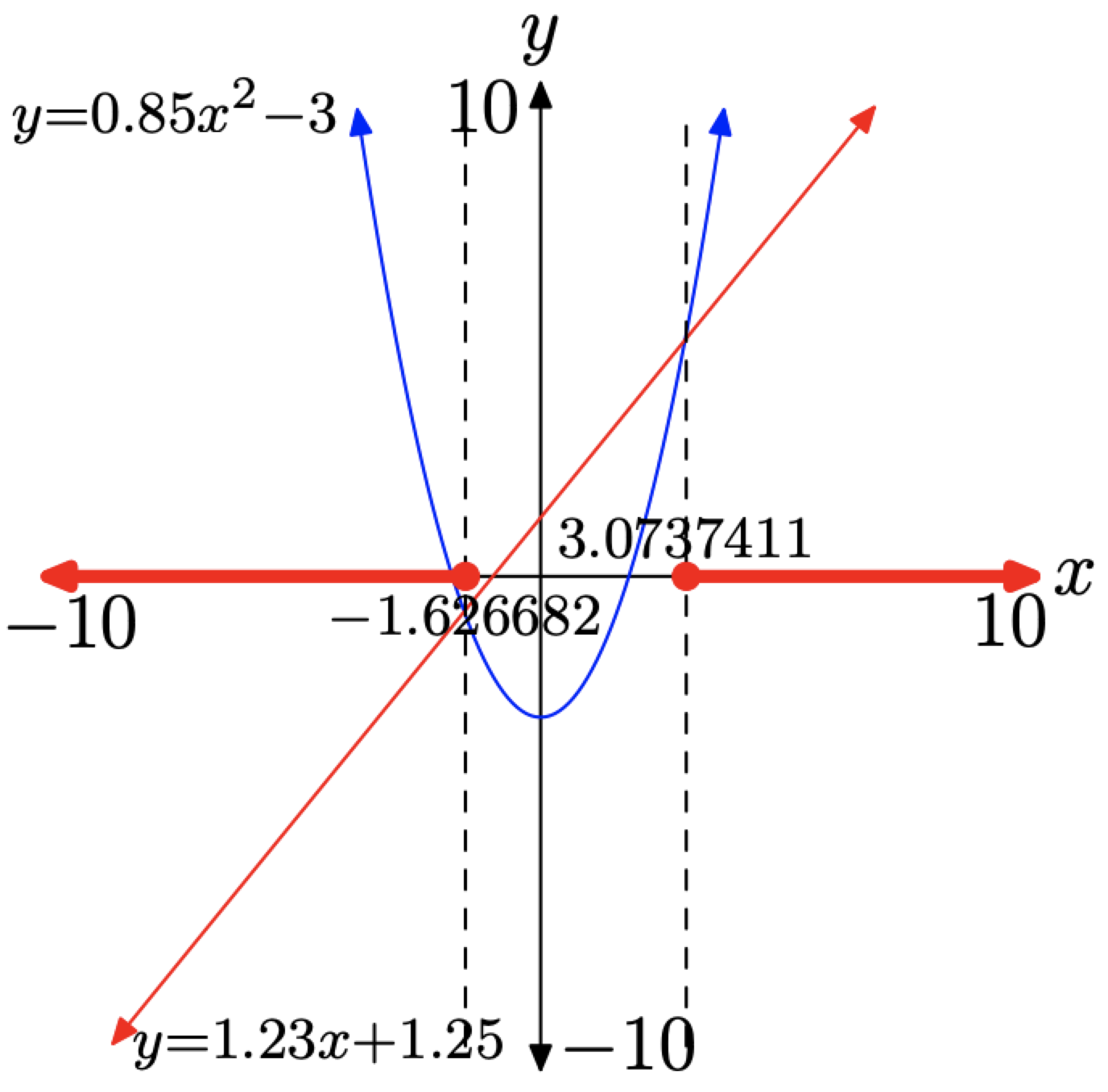
Ahora resumimos nuestros resultados creando un sistema de coordenadas, etiquetando los ejes y escalando los ejes con los valores de los parámetros de ventana xmin, xmax, ymin e ymax. Copiamos la imagen en nuestra ventana de visualización en este sistema de coordenadas, etiquetando cada gráfica con su ecuación. Luego dibujamos líneas verticales discontinuas a través de cada punto de intersección, como se muestra en la Figura\(\PageIndex{14}\).

Estamos resolviendo la desigualdad\(0.85 x^{2}-3 \geq 1.23 x+1.25\). La solución será la unión de las soluciones de\(0.85 x^{2}-3>1.23 x+1.25\) y\(0.85 x^{2}-3=1.23 x+1.25\).

• Para resolver\(0.85 x^{2}-3>1.23 x+1.25\), observamos dónde se\(y=0.85 x^{2}-3\) encuentra la gráfica de encima de la gráfica de\(y=1.23 x+1.25\) y sombreamos los valores x correspondientes

Figura\(\PageIndex{14}\). Resumiendo la solución de\(0.85 x^{2}-3 \geq 1.23 x+1.25\).

en el eje x. En este caso, la gráfica de\(y=0.85 x^{2}-3\) se encuentra por encima de la gráfica de\(y=1.23 x+1.25\) para valores de x que se encuentran fuera de nuestras líneas verticales discontinuas.

• Para resolver\(0.85 x^{2}-3=1.23 x+1.25\), observamos dónde la gráfica de\(y=0.85 x^{2}-3\) cruza la gráfica de\(y = 1.23x + 1.25\) y sombrea los valores x correspondientes en el eje x. Es por ello que los puntos en\(x \approx-1.626682\) y\(x \approx 3.0737411\) están “llenos”.

Así, todos los valores de x que son menores o iguales a −1.626682 o mayores o iguales a 3.0737411 son soluciones. Es decir, la solución de la desigualdad\(0.85x^{2} − 3 > 1.23x + 1.25\) es aproximadamente

\[(-\infty,-1.626682] \cup[3.0737411, \infty)=\{x : x \leq-1.626682 \text { or } x \geq 3.0737411\}\]

Comparación de funciones con cero

Cuando evaluamos una función f a un valor particular de x, solo uno de los tres resultados es posible. O bien

\[f(x)=0, \quad \text { or } \quad f(x)>0, \quad \text { or } \quad f(x)<0\]

Es decir, o f (x) es igual a cero, o f (x) es positivo, o f (x) es negativo. No hay otras posibilidades.

Podríamos empezar de nuevo, tomando un enfoque completamente nuevo, o podemos construir sobre lo que ya sabemos. Elegimos este último enfoque. Supongamos que se nos pide comparar f (x) con cero? ¿Es igual a cero, es mayor que cero, o es menor que cero?

Establecemos g (x) = 0. Ahora bien, si queremos comparar la función f con cero, solo necesitamos comparar f con g, lo que ya sabemos hacer. Para encontrar donde f (x) = g (x), observamos donde se cruzan las gráficas de f y g, para encontrar donde f (x) > g (x), observamos dónde se encuentra la gráfica de f por encima de la gráfica de g, y finalmente, para encontrar donde f (x) < g (x), simplemente notamos dónde se encuentra la gráfica de f debajo de la gráfica de g.

Sin embargo, la gráfica de g (x) = 0 es una línea horizontal coincidente con el eje x. En efecto, g (x) = 0 es la ecuación del eje x. Este argumento lleva a los siguientes resultados clave.

resumen

• La solución de f (x) = 0 es el conjunto de todos x para el cual la gráfica de f se cruza con el eje x.
• La solución de f (x) > 0 es el conjunto de todos x para el que la gráfica de f se encuentra estrictamente por encima del eje x.
• La solución de f (x) < 0 es el conjunto de todos x para el que la gráfica de f se encuentra estrictamente por debajo del eje x.

Por ejemplo:

• Para encontrar la solución de f (x) = 0 en la Figura\(\PageIndex{15}\) (a), simplemente notamos dónde la gráfica de f cruza el eje x en la Figura\(\PageIndex{15}\) (a). Así, la solución de f (x) = 0 es x = 1.
• Para encontrar la solución de f (x) > 0 en la Figura\(\PageIndex{15}\) (b), simplemente observamos donde la gráfica de f se encuentra por encima del eje x en la Figura\(\PageIndex{15}\) (b), que está a la derecha de la línea discontinua vertical a través de x = 1. Así, la solución de f (x) > 0 es\((1, \infty)=\{x : x>1\}\).
• Para encontrar la solución de f (x) < 0 en la Figura\(\PageIndex{15}\) (c), simplemente observamos donde la gráfica de f se encuentra debajo del eje x en la Figura\(\PageIndex{15}\) (c), que está a la izquierda de la línea discontinua vertical en x = 1. Así, la solución de f (x) < 0 es\((-\infty, 1)=\{x : x<1\}\).

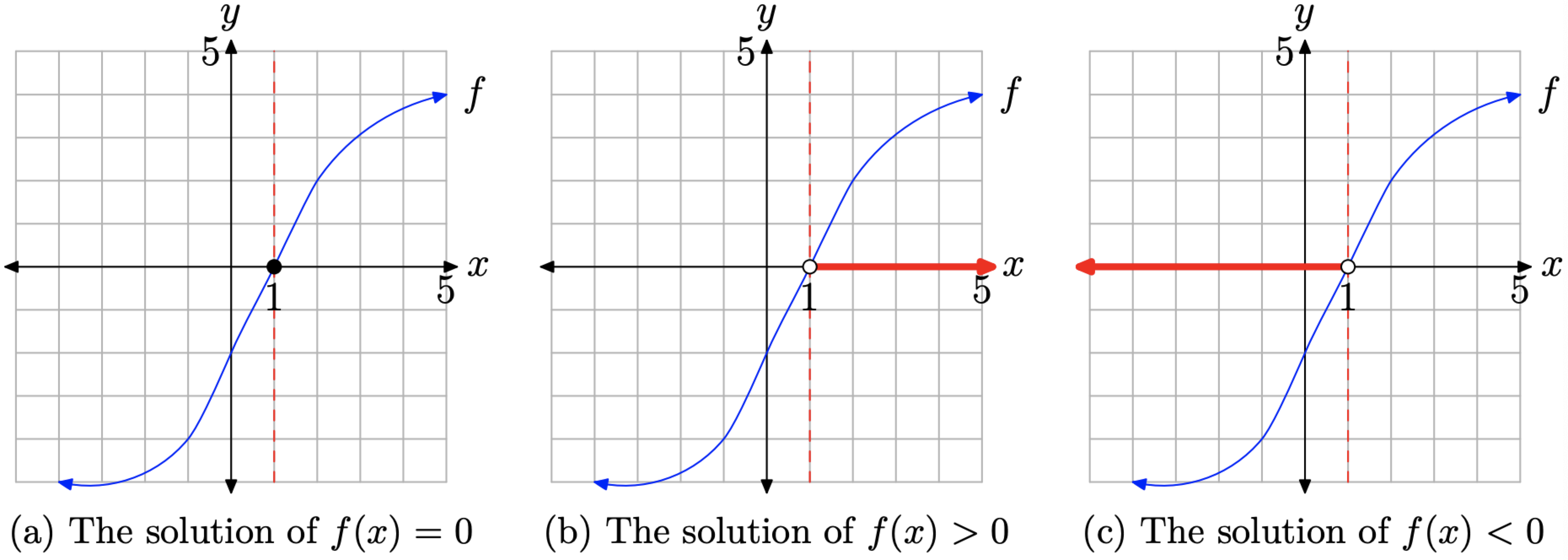
Figura\(\PageIndex{15}\). Comparando la función f con cero.

A continuación definimos alguna terminología importante.

Definición

Si f (a) = 0, entonces a se llama cero de la función f. La gráfica de f interceptará el eje x en\((a, 0)\), un punto llamado la intercepción x de la gráfica de f.

Tu calculadora tiene una utilidad que te ayudará a encontrar los ceros de una función.

Ejemplo\(\PageIndex{6}\)

Usar una calculadora gráfica para resolver la desigualdad

\[0.25 x^{2}-1.24 x-3.84 \leq 0\]

Solución

Tenga en cuenta que esta desigualdad tiene la forma\(f(x) \leq 0\), donde\(f(x)=0.25 x^{2}-1.24 x-3.84\). Nuestra estrategia será dibujar la gráfica de f, luego determinar dónde se encuentra la gráfica de f debajo o en el eje x.

Procedemos de la siguiente manera:

• Primero, cargue la función f (x) = 0.25x 2 − 1.24x − 3.84 en el Y1 en el menú Y= de su calculadora. Seleccione 6:ZStandard en el menú ZOOM para producir la imagen en la Figura\(\PageIndex{16}\) (a).
• Presione 2nd CALC para abrir el menú que se muestra en la Figura\(\PageIndex{16}\) (b), luego seleccione 2:cero para iniciar la utilidad que encontrará un cero de la función (una intercepción x de la gráfica).
• La calculadora pide un “Límite a la izquierda”, así que usa tus teclas de flecha para mover el cursor ligeramente hacia la izquierda de la intersección x más a la izquierda de la gráfica, como se muestra en la Figura\(\PageIndex{16}\) (c). Presiona ENTRAR para grabar este “Izquierdo Bound”.
• Luego, la calculadora pide un “Encuadernado a la derecha”, así que usa tus teclas de flecha para mover el cursor ligeramente a la derecha de la intersección x, como se muestra en la Figura\(\PageIndex{16}\) (d). Presiona ENTRAR para grabar este “Right Bound”.

Figura (\ PageIndex {16}\). Encontrar una intercepción cero o x con la calculadora.

• La calculadora responde marcando los límites izquierdo y derecho en la pantalla, como se muestra en la Figura (\ PageIndex {17}\) (a), luego le pide que haga una suposición de inicio razonable para la intercepción cero o x. Puede usar las teclas de flecha para mover el cursor a cualquier punto, siempre y cuando el cursor permanezca entre las marcas de izquierda y derecha en la ventana de visualización. Por lo general, simplemente dejamos el cursor donde está y presionamos el botón ENTER para grabar esta suposición. Te sugerimos que hagas eso también.
• La calculadora responde encontrando las coordenadas de la intersección x, como se muestra en la Figura (\ PageIndex {17}\) (b). Tenga en cuenta que la coordenada x de la intersección x es aproximadamente −2.157931.
• Repita el procedimiento para encontrar las coordenadas de la intersección x más a la derecha. El resultado se muestra en la Figura (\ PageIndex {17}\) (c). Tenga en cuenta que la coordenada x de la intersección es aproximadamente 7.1179306.

El paso final es la interpretación de los resultados y el registro de nuestra solución en nuestro trabajo de tarea. Refiriéndose al Resumen 7 Lineamientos, se nos presenta la gráfica que se muestra en la Figura (\ PageIndex {18}\).

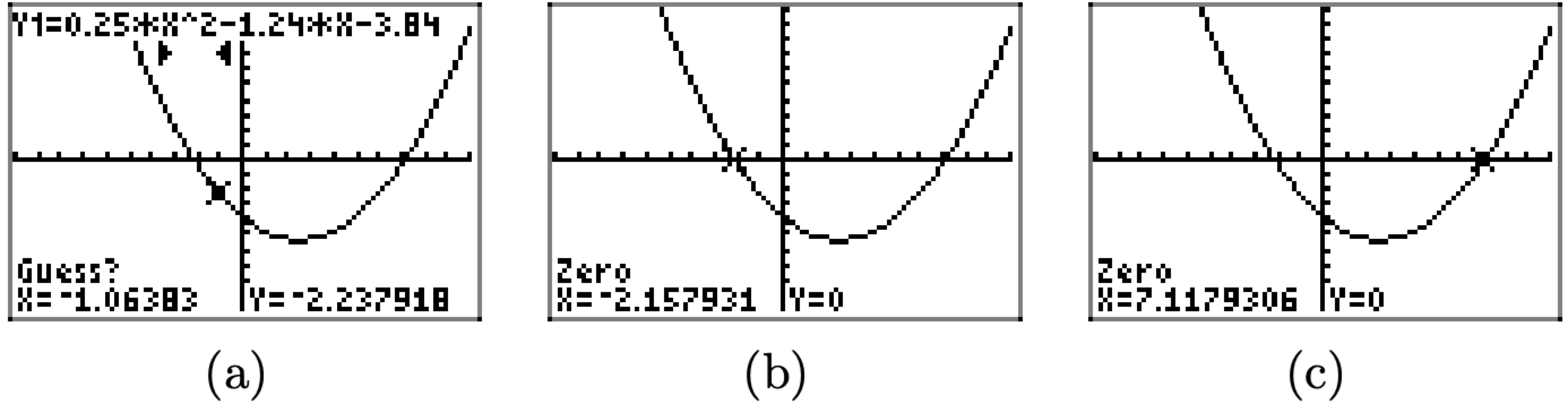
Figura (\ PageIndex {17}\). Encontrar una intercepción cero o x con la calculadora.

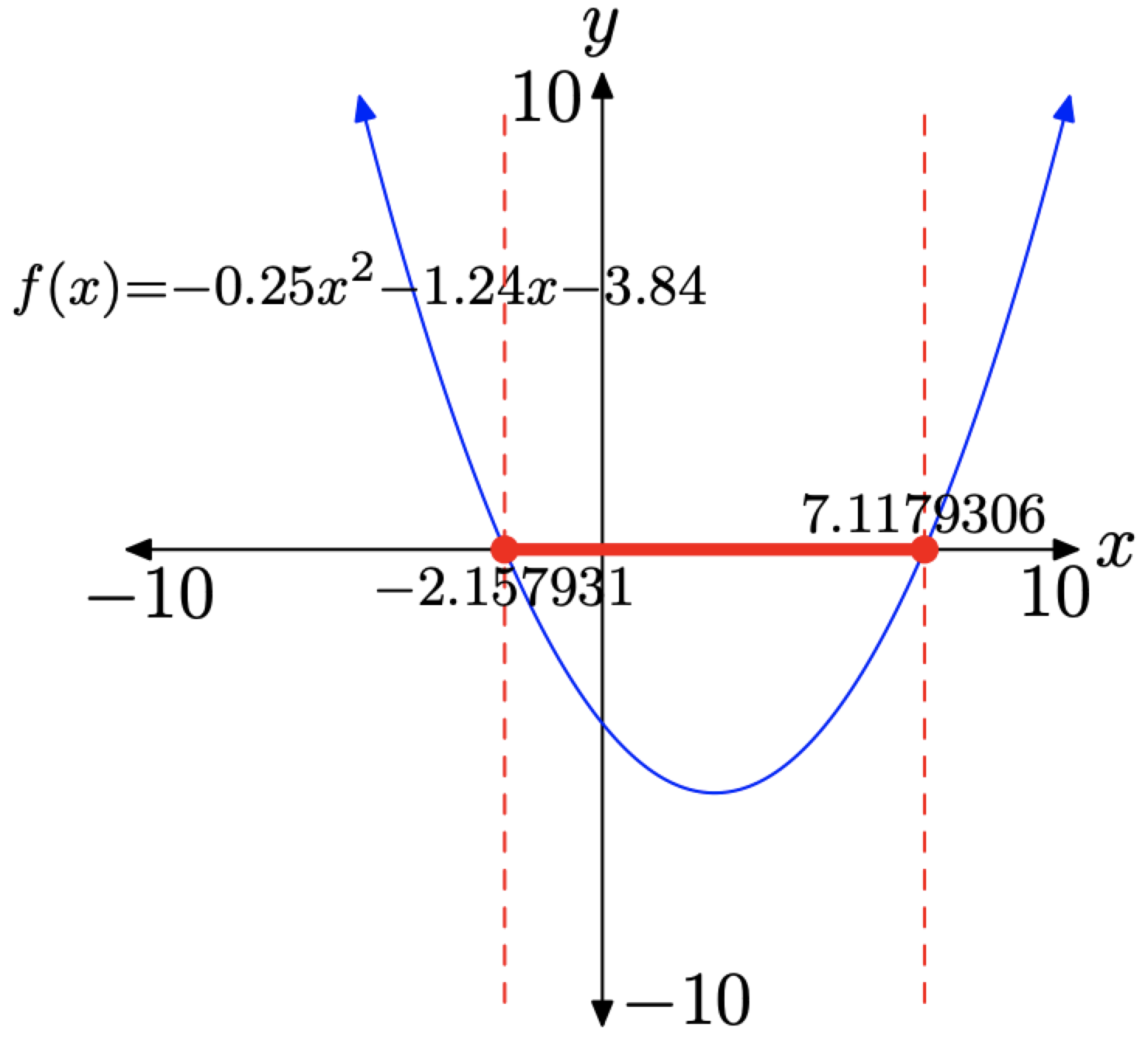
Figura (\ PageIndex {18}\). La solución de\(0.25 x^{2}- 1.24 x-3,84 \leq 0 .\).

Varios comentarios están en regla. Observando que\(f(x)=0.25 x^{2}-1.24 x-3.84\), observamos:

1. Las soluciones de f (x) = 0 son los puntos donde la gráfica cruza el eje x. Es por eso que los puntos (−2.157931, 0) y (7.1179306, 0) son sombreados y rellenados en Figura (\ PageIndex {18}\).
2. Las soluciones de f (x) < 0 son aquellos valores de x para los cuales la gráfica de f cae estrictamente por debajo del eje x. Esto ocurre para todos los valores de x entre −2.157931 y 7.1179306. Estos puntos también están sombreados en el eje x en la Figura (\ PageIndex {18}\).
3. Finalmente, la solución de\(f(x) \leq 0\) es la unión de estos dos sombreados, los cuales describimos en notación interval y set-builder de la siguiente manera:

\[[-2.157931,7.1179306]=\{x :-2.157931 \leq x \leq 7.1179306\}\]