4.3: Ecuaciones de Valor Absoluto

En la sección anterior, definimos

\[|x|=\left\{\begin{array}{ll}{-x,} & {\text { if } x<0} \\ {x,} & {\text { if } x \geq 0}\end{array}\right.\]

y vimos que la gráfica de la función de valor absoluto definida por f (x) = |x| tiene la “forma de V” que se muestra en la Figura\(\PageIndex{1}\).

Figura\(\PageIndex{1}\). La gráfica de la función de valor absoluto f (x) = |x|.

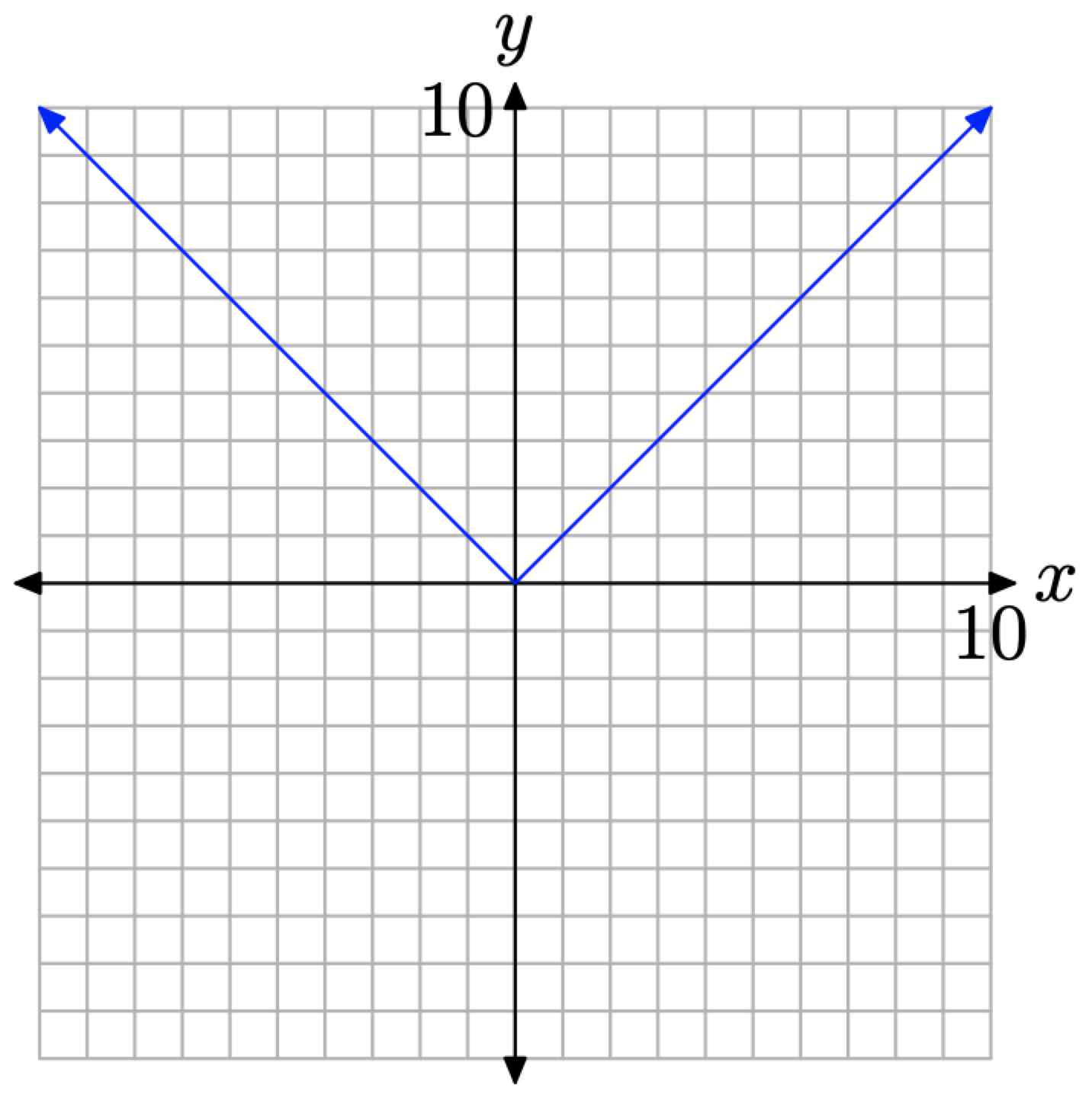
Es importante señalar que la ecuación de la rama izquierda de la “V” es y = −x. Los puntos típicos de esta rama son (−1, 1), (−2, 2), (−3, 3), etc. Es igualmente importante señalar que la rama derecha de la “V” tiene la ecuación y = x. Los puntos típicos en esta rama son (1, 1), (2, 2), (3, 3), etc.

Resolviendo |x| = a

Ahora discutiremos las soluciones de la ecuación

\[|x|=a\]

Hay tres casos distintos para discutir, cada uno de los cuales depende del valor y signo del número a.

• Caso I: a < 0

Si a < 0, entonces la gráfica de y = a es una línea horizontal que se encuentra estrictamente por debajo del eje x, como se muestra en la Figura\(\PageIndex{2}\) (a). En este caso, la ecuación |x| = a no tiene soluciones porque las gráficas de y = a e y = |x| no se cruzan.

• Caso II: a = 0

Si a = 0, entonces la gráfica de y = 0 es una línea horizontal que coincide con el eje x, como se muestra en la Figura\(\PageIndex{2}\) (b). En este caso, la ecuación |x| = 0 tiene la solución única x = 0, porque la línea horizontal y = 0 cruza la gráfica de y = |x| en exactamente un punto, en x = 0.

• Caso III: a > 0

Si a > 0, entonces la gráfica de y = a es una línea horizontal que se encuentra estrictamente por encima del eje x, como se muestra en la Figura\(\PageIndex{2}\) (c). En este caso, la ecuación |x| = a tiene dos soluciones, porque las gráficas de y = a e y = |x| tienen dos puntos de intersección.

Recordemos que la rama izquierda de y = |x| tiene la ecuación y = −x, y los puntos en esta rama tienen la forma (−1, 1), (−2, 2), etc. Debido a que el punto donde la gráfica de y = a cruza la rama izquierda de y = |x| tiene la coordenada y = a, la coordenada x de este punto de intersección es x = −a. Esta es una solución de |x| = a.

Recordemos que la rama derecha de y = |x| tiene la ecuación y = x, y los puntos en esta rama tienen la forma (1, 1), (2, 2), etc. Debido a que el punto donde la gráfica de y = a se cruza con la rama derecha de y = |x| tiene la coordenada y = a, la coordenada x de este punto de intersección es x = a. Esta es la segunda solución de |x| = a.

Figura\(\PageIndex{2}\). La solución de |x| = a tiene tres casos.

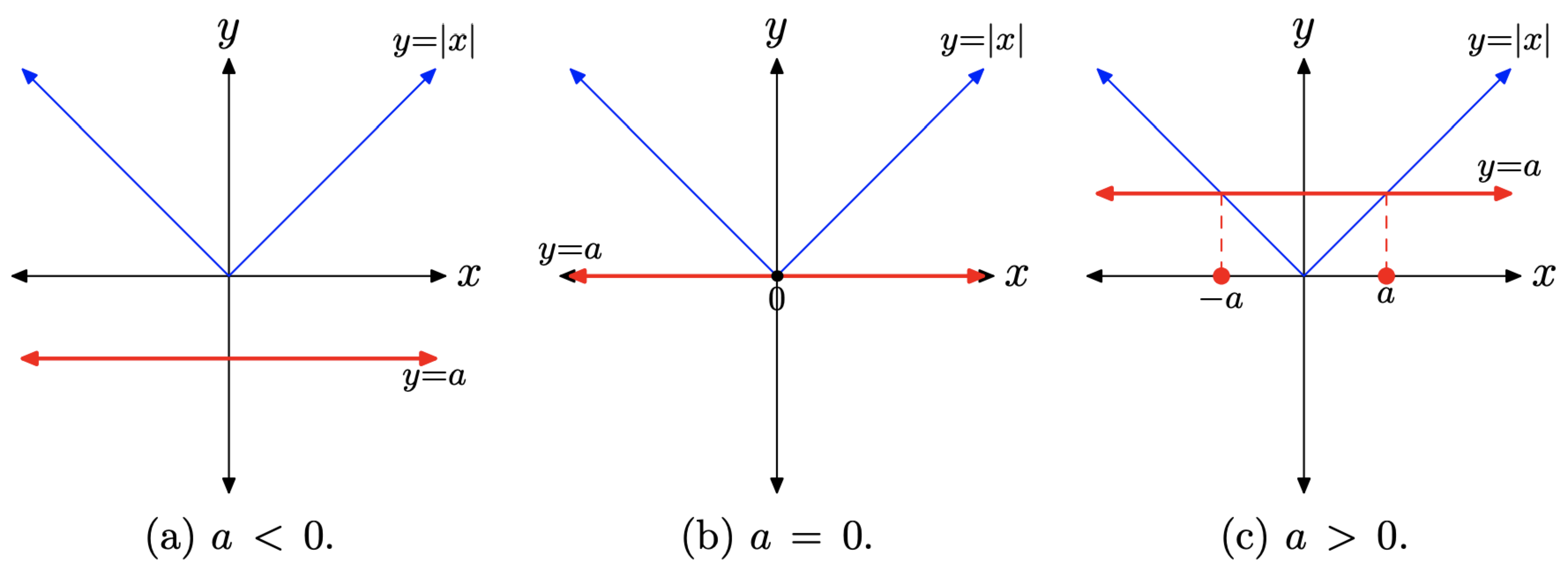
Esta discusión lleva al siguiente resultado clave.

Propiedad 2

La solución de |x| = a depende del valor y signo de a.

• Caso I: a < 0

La ecuación |x| = a no tiene soluciones.

• Caso II: a = 0

La ecuación |x| = 0 tiene una solución, x = 0.

• Caso III: a > 0

La ecuación |x| = a tiene dos soluciones, x = −a o x = a.

Veamos algunos ejemplos.

Ejemplo\(\PageIndex{1}\)

Resolver |x| = −3 para x.

Solución

La gráfica del lado izquierdo de |x| = −3 es la “V” de la Figura\(\PageIndex{2}\) (a). La gráfica del lado derecho de |x| = −3 es una línea horizontal tres unidades por debajo del eje x. Este tiene la forma del boceto de la Figura\(\PageIndex{2}\) (a). Las gráficas no se cruzan. Por lo tanto, la ecuación |x| = −3 no tiene soluciones.

Un enfoque alternativo es considerar el hecho de que el valor absoluto de x nunca puede ser igual a −3. El valor absoluto de un número es siempre no negativo (ya sea cero o positivo). De ahí que la ecuación |x| = −3 no tiene soluciones.

Ejemplo\(\PageIndex{2}\)

Resolver |x| = 0 para x

Solución

Este es el caso mostrado en la Figura\(\PageIndex{2}\) (b). La gráfica del lado izquierdo de |x| = 0 cruza la gráfica del lado derecho de |x| = 0 en x = 0. Así, la única solución de |x| = 0 es x = 0.

Pensando en esto algebraicamente en vez de gráficamente, sabemos que 0 = 0, pero no hay otro número con un valor absoluto de cero. Entonces, intuitivamente, la única solución de |x| = 0 es x = 0.

Ejemplo\(\PageIndex{3}\)

Resolver |x| = 4 para x.

Solución

La gráfica del lado izquierdo de |x| = 4 es la “V” de la Figura\(\PageIndex{2}\) (c). La gráfica del lado derecho es una línea horizontal 4 unidades por encima del eje x. Esto tiene la forma del boceto en la Figura\(\PageIndex{2}\) (c). Las gráficas se cruzan en (−4, 4) y (4, 4). Por lo tanto, las soluciones de |x| = 4 son x = −4 o x = 4.

Alternativamente, | − 4| = 4 y |4| = 4, pero ningún otro número real tiene un valor absoluto igual a 4. De ahí que las únicas soluciones de |x| = 4 son x = −4 o x = 4.

Ejemplo\(\PageIndex{4}\)

Resuelve la ecuación |3 − 2x| = −8 para x.

Solución

Si la ecuación fuera |x| = −8, no dudaríamos. La ecuación |x| = −8 no tiene soluciones. Sin embargo, el razonamiento aplicado al caso simple |x| = −8 funciona igualmente bien con la ecuación |3 − 2x| = −8. El lado izquierdo de esta ecuación debe ser no negativo, por lo que su gráfica debe estar por encima o sobre el eje x. El lado derecho de |3−2x| = −8 es una línea horizontal 8 unidades por debajo del eje x. Las gráficas no pueden cruzarse, por lo que no hay solución.

Podemos verificar este argumento con la calculadora gráfica. Cargue los lados izquierdo y derecho de |3 − 2x| = −8 en Y1 e Y2, respectivamente, como se muestra en la Figura\(\PageIndex{3}\) (a). Presione el botón MATH en su calculadora y luego con la flecha derecha hacia el menú NUM, como se muestra en la Figura\(\PageIndex{3}\) (b). Use 1:abs (para ingresar el valor absoluto que se muestra en Y1 en la Figura\(\PageIndex{3}\) (a). En el menú ZOOM, seleccione 6:ZStandard para producir la imagen que se muestra en la Figura\(\PageIndex{3}\) (c).

Tenga en cuenta que como se predijo anteriormente, la gráfica de y = |3 − 2x| se encuentra sobre o por encima del xeje y la gráfica de y = −8 se encuentra estrictamente por debajo del eje x. De ahí que las gráficas no puedan cruzarse y la ecuación |3 − 2x| = −8 no tiene soluciones.

Figura\(\PageIndex{3}\). Usando la calculadora gráfica para examinar la solución de |3 − 2x| = −8.

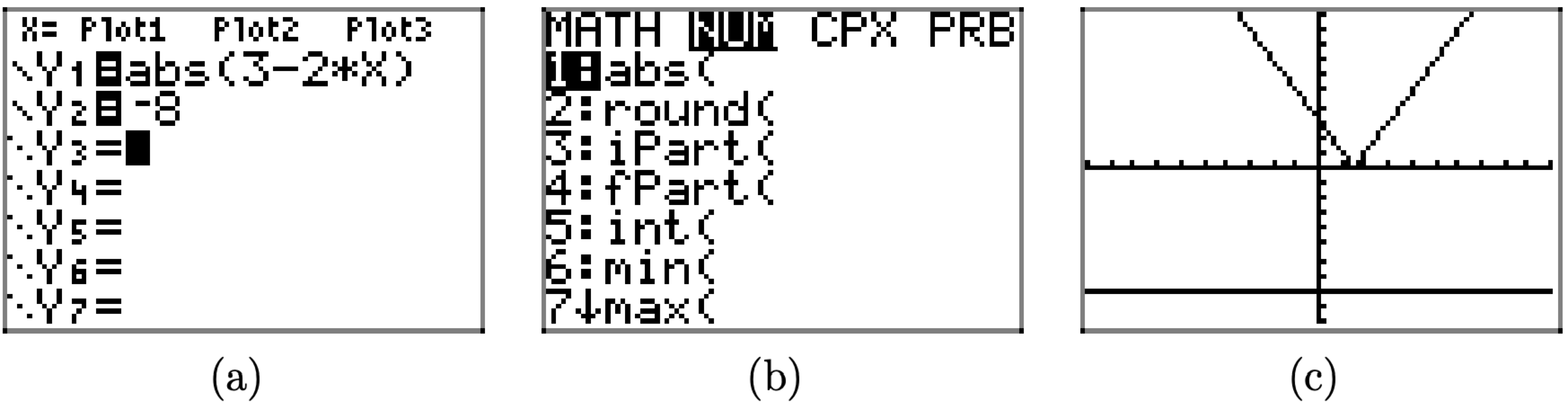
Alternativamente, podemos proporcionar una solución completamente intuitiva de |3 − 2x| = −8 argumentando que el lado izquierdo de esta ecuación no es negativo, pero el lado derecho es negativo. Esta es una situación imposible. De ahí que la ecuación no tenga soluciones.

Ejemplo\(\PageIndex{5}\)

Resuelve la ecuación |3 − 2x| = 0 para x.

Solución

Hemos argumentado que la única solución de |x| = 0 es x = 0. Razonamiento similar señala que |3 − 2x| = 0 solo cuando 3 − 2x = 0. Resolvemos esta ecuación de manera independiente.

\[\begin{aligned} 3-2 x &=0 \\-2 x &=-3 \\ x &=\frac{3}{2} \end{aligned}\]
Así, la única solución de |3 − 2x| = 0 es x = 3/2.

Cabe señalar que la “punta” o “vértice” de la “V” en la Figura\(\PageIndex{3}\) (c) se ubica en x = 3/2. Esta es la única ubicación donde se cruzan las gráficas de y = |3 − 2x| e y = 0.

Ejemplo\(\PageIndex{6}\)

Resuelve la ecuación |3 − 2x| = 6 para x.

Solución

En este ejemplo, la gráfica de y = 6 es una línea horizontal que se encuentra 6 unidades por encima del eje x, y la gráfica de y = |3 − 2x| cruza la gráfica de y = 6 en dos ubicaciones. Se puede utilizar la utilidad intersectar para encontrar los puntos de intersección de las gráficas, como tenemos en la Figura\(\PageIndex{4}\) (b) y (c).

Figura\(\PageIndex{4}\). Usando la calculadora gráfica para encontrar dos soluciones de |3 − 2x| = 6.

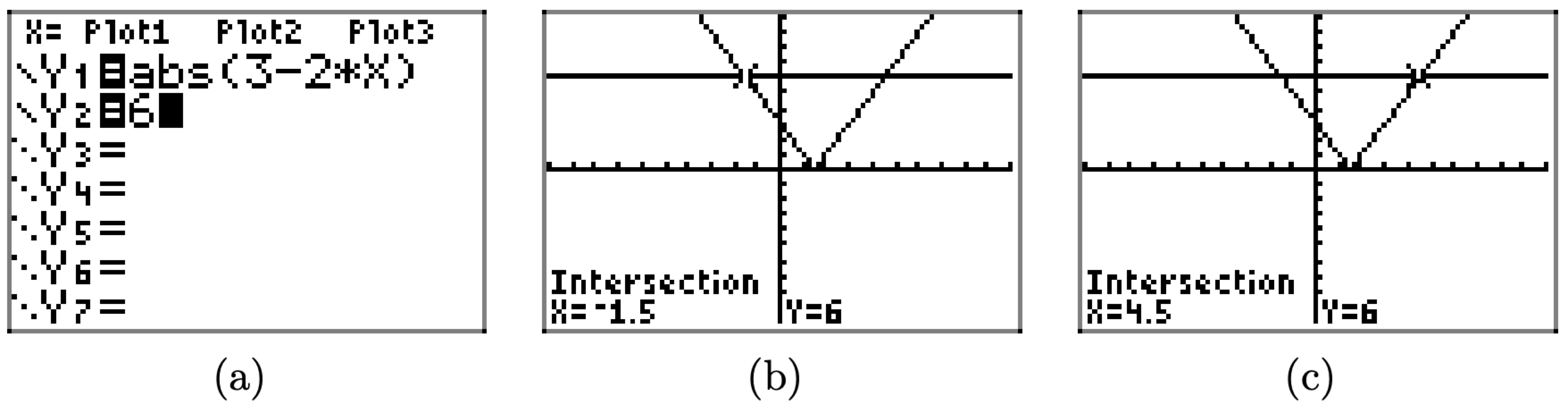
Necesitamos una forma de resumir este enfoque de calculadora gráfica en nuestro trabajo de tarea. Primero, dibuje un facsímil razonable de la ventana de visualización de su calculadora en su papel de tarea. Usa una regla para dibujar todas las líneas. Complete la siguiente lista de verificación.

• Etiquete cada eje, en este caso con x e y.
• Escala cada eje. Para ello, presione el botón VENTANA en su calculadora, luego reporte los valores de xmin, xmax, ymin e ymax en el eje apropiado.
• Etiquete cada gráfica con su ecuación.
• Suelte líneas verticales discontinuas desde los puntos de intersección hasta el eje x. Sombra y etiquete estas soluciones de la ecuación en el eje x.

Siguiendo las pautas de la lista de verificación anterior, obtenemos la imagen en la Figura\(\PageIndex{5}\).

Figura\(\PageIndex{5}\). Reportando una solución gráfica de |3 − 2x| = 6.

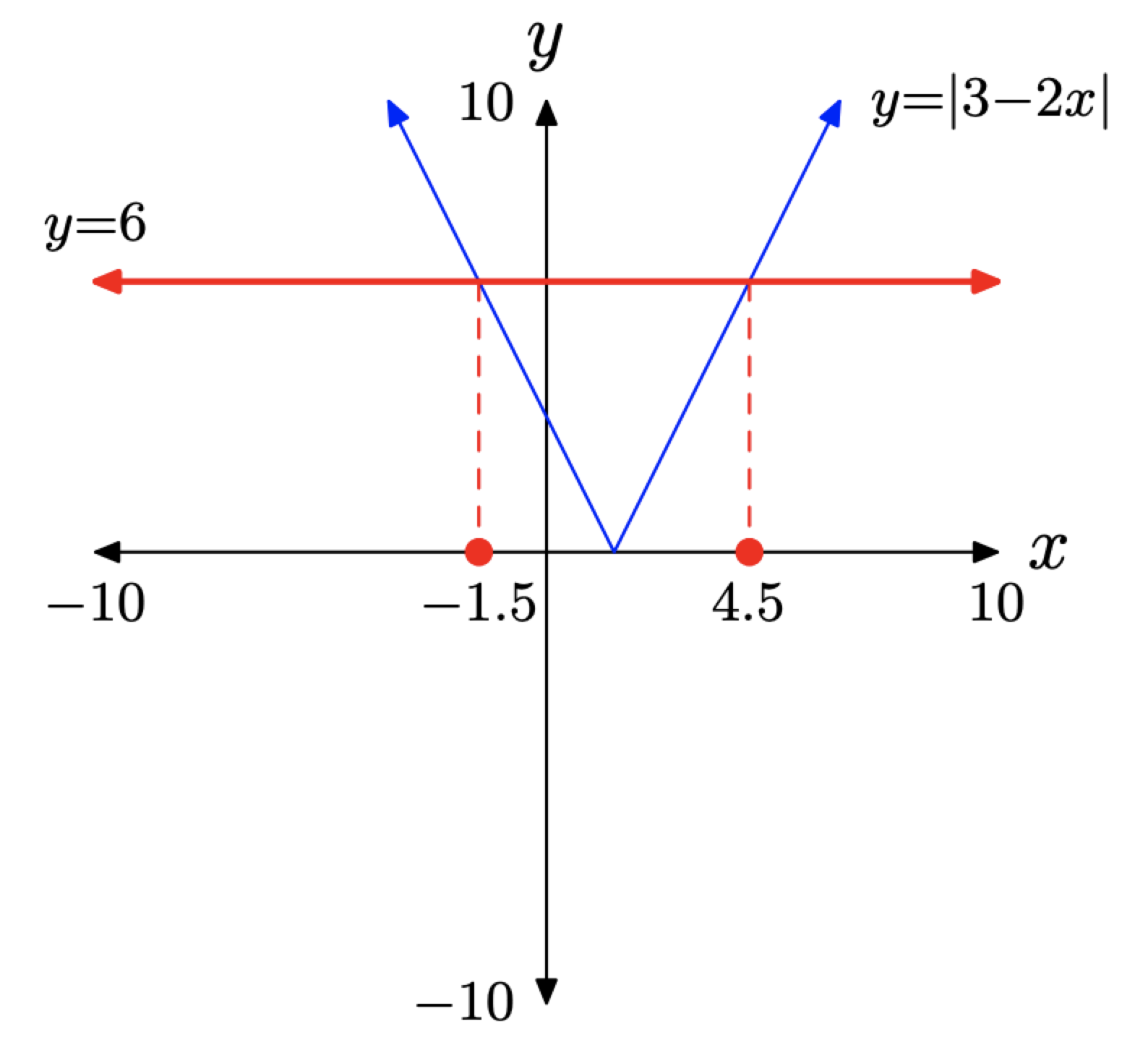
Aproximación algebraica. También se puede utilizar una técnica algebraica para encontrar las dos soluciones de |3 − 2x| = 6. Tanto como |x| = 6 tiene soluciones x = −6 o x = 6, la ecuación

\[|3-2 x|=6\]

es posible solo si la expresión dentro de los valores absolutos es igual a −6 o 6. Por lo tanto, escriba

\[3-2 x=-6 \qquad \text { or } \qquad 3-2 x=6\]

y resolver estas ecuaciones de forma independiente

\[\begin{array}{rlrrrl}{3-2 x}&{=}&{-6} & {\text { or }} & {3-2 x}&{=}&{6} \\ {-2 x}&{=}&{-9} && {-2 x}&{=}&{3} \\ {x}&{=}&{\frac{9}{2}} && {x}&{=}&{-\frac{3}{2}}\end{array}\]

Debido a que −3/2 = −1.5 y 9/2 = 4.5, estas soluciones exactas concuerdan exactamente con las soluciones gráficas de la Figura\(\PageIndex{4}\) (b) y (c).

Resumamos la técnica involucrada en resolver este importante caso.

Nota

Resolviendo |expresión| = a, cuando a > 0. Para resolver la ecuación

\[| \text { expression } |=a, \quad \text { when } a>0\]

conjunto

\[\text { expression }=-a \qquad \text { or } \qquad \text { expression }=a\]

luego resolver cada una de estas ecuaciones de forma independiente.

Por ejemplo:

• Resolver |2x + 7| = 5, establecer\[2x + 7 = −5 \qquad or \qquad 2x + 7 = 5\], luego resolver cada una de estas ecuaciones de forma independiente.

• Para resolver |3 − 5x| = 9, establecer\[3 − 5x = −9 \qquad or \qquad 3 − 5x = 9\], luego resolver cada una de estas ecuaciones de forma independiente.

• Tenga en cuenta que esta técnica no debe aplicarse a la ecuación |2x + 11| = −10, porque el lado derecho de la ecuación no es un número positivo. En efecto, en este caso, ningún valor de x hará que el lado izquierdo de esta ecuación sea igual a −10, por lo que la ecuación no tiene soluciones.

A veces tenemos que hacer un poco de álgebra antes de eliminar las barras de valor absoluto.

Ejemplo\(\PageIndex{7}\)

Resuelve la ecuación\[|x+2|+3=8\] para x.

Solución

Primero, restar 3 de ambos lados de la ecuación. \[\begin{aligned}|x+2|+3 &=8 \\|x+2|+3-3 &=8-3 \end{aligned}\]

Esto simplifica a\[|x+2|=5\]

Ahora, ya sea\[x+2=-5 \qquad \text { or } \qquad x+2=5\]

cada uno de los cuales se puede resolver por separado.

\[\begin{array}{rrlrrl}{x+2} & {=} & {-5} & {\text { or }} & {x+2} & {=} & {5} \\ {x+2-2} & {=} & {-5-2} && {x+2-2} & {=} & {5-2} \\ {x} & {=} & {-7} && {x} & {=} & {3}\end{array}\]

Ejemplo\(\PageIndex{8}\)

Resuelve la ecuación\[3|x-5|=6\] para x.

Solución

Primero, divide ambos lados de la ecuación por 3

\[\begin{aligned} 3|x-5| &=6 \\ \frac{3|x-5|}{3} &=\frac{6}{3} \end{aligned}\]

Esto simplifica a\[|x-5|=2\]

Ahora, ya sea\[x-5=-2 \qquad \text { or } \qquad x-5=2\]

cada uno de los cuales se puede resolver por separado.

\[\begin{array}{rllrrl}{x-5} & {=} & {-2} & {\text { or }} & {x-5} & {=} & {2} \\ {x-5+5} & {=} & {-2+5} && {x-5+5} & {=} & {2+5} \\ {x} & {=} & {3} && {x} & {=} & {7}\end{array}\]

Propiedades de Valor Absoluto

Un ejemplo motivará la necesidad de alguna discusión sobre las propiedades de valor absoluto.

Ejemplo\(\PageIndex{9}\)

Resuelve la ecuación\[\left|\frac{x}{2}-\frac{1}{3}\right|=\frac{1}{4}\] para x.

Solución

Es tentador multiplicar ambos lados de esta ecuación por un denominador común de la siguiente manera.

\[\begin{array}{l}{\left|\dfrac{x}{2}-\dfrac{1}{3}\right|=\dfrac{1}{4}} \\ {12\left|\dfrac{x}{2}-\dfrac{1}{3}\right|=12\left(\dfrac{1}{4}\right)}\end{array}\]

Si es permisible mover el 12 dentro de los valores absolutos, entonces podríamos proceder de la siguiente manera.

\[\begin{aligned}\left|12\left(\frac{x}{2}-\frac{1}{3}\right)\right| &=3 \\|6 x-4| &=3 \end{aligned}\]

Suponiendo por el momento que este último movimiento es permisible, ya sea

\[6 x-4=-3 \qquad \text { or } \qquad 6 x-4=3\]

Cada uno de estos se puede resolver por separado, primero sumando 4 a ambos lados de las ecuaciones, luego dividiendo por 6.

\[\begin{array}{rllrrl}{6 x-4} & {=} & {-3} & {\text { or }} & {6 x-4} & {=} & {3} \\ {6 x} & {=} & {1} & &{6 x} & {=} & {7} \\ {x} & {=} & {1 / 6} && {x} & {=} & {7 / 6}\end{array}\]

Como hemos utilizado un movimiento algo cuestionable para obtener estas soluciones, sería prudente verificar nuestros resultados. Primero, sustituya x = 1/6 en la ecuación original.

\[\begin{aligned}\left|\frac{x}{2}-\frac{1}{3}\right| &=\frac{1}{4} \\\left|\frac{1 / 6}{2}-\frac{1}{3}\right| &=\frac{1}{4} \\\left|\frac{1}{12}-\frac{1}{3}\right| &=\frac{1}{4} \end{aligned}\]

Escribe fracciones equivalentes con un denominador común y resta.

\[\begin{aligned}\left|\frac{1}{12}-\frac{4}{12}\right| &=\frac{1}{4} \\\left|-\frac{3}{12}\right| &=\frac{1}{4} \\\left|-\frac{1}{4}\right| &=\frac{1}{4} \end{aligned}\]

Claramente, x = 1/6 cheques. Dejaremos el cheque de la segunda solución a nuestros lectores.

Bueno, hemos comprobado nuestras soluciones y son correctas, así que debe darse el caso de que

\[12\left|\frac{x}{2}-\frac{1}{3}\right|=\left|12\left(\frac{x}{2}-\frac{1}{3}\right)\right|\]

Pero, ¿por qué? Después de todo, las barras de valores absolutos, aunque actúan como símbolos de agrupación, tienen un significado un poco más restrictivo que los símbolos de agrupación ordinarios como paréntesis, corchetes y llaves.

Se establece la primera propiedad de valores absolutos.

Propiedad

Si a y b son números reales, entonces

\[|a b|=|a||b|\]

Podemos demostrar la validez de esta propiedad simplemente verificando casos.

• Si a y b son ambos números reales positivos, entonces también lo es ab y\(|a||b|=a b\). Por otro lado,\(|a||b|=a b\). Así,\(|ab| = |a||b|\).
• Si a y b son números reales negativos, entonces ab es positivo y\(|ab| = ab\). Por otro lado,\(|a||b| = (−a)(−b) = ab\). Así,\(|ab| = |a||b|\).

Dejaremos como ejercicios el comprobante de los dos casos restantes. Podemos usar\(|a||b| = |ab|\) para demostrar que

\[12\left|\frac{x}{2}-\frac{1}{3}\right|=|12|\left|\frac{x}{2}-\frac{1}{3}\right|=\left|12\left(\frac{x}{2}-\frac{1}{3}\right)\right|\]

Esto valida el método de ataque que usamos para resolver la ecuación (12) en Ejemplo\(\PageIndex{9}\).

Advertencia 14

Por otro lado, no está permitido multiplicar por un número negativo y simplemente deslizar el número negativo dentro de las barras de valor absoluto. Por ejemplo,

\[-2|x-3|=|-2(x-3)|\]

es claramente un error (bueno, sí funciona para x = 3). Para cualquier x excepto 3, el lado izquierdo de este resultado es un número negativo, pero el lado derecho es un número positivo. Claramente no son iguales.

De manera similar, se puede demostrar una segunda propiedad útil que involucra valor absoluto.

Definición

Si a y b son números reales, entonces\[\left|\frac{a}{b}\right|=\frac{|a|}{|b|}\] siempre que, por supuesto, eso\(b \neq 0\).

Nuevamente, esto se puede probar comprobando cuatro casos. Por ejemplo, si a es un número real positivo y b es un número real negativo, entonces a/b es negativo y\(|a/b| = −a/b\). Por otro lado,\(|a|/|b| = a/(−b) = −a/b\).

Dejamos como ejercicios el comprobante de los tres casos restantes.

Esta propiedad es útil en ciertas situaciones. Por ejemplo, si deseas dividir\(|2x − 4|\) por 2, procederías de la siguiente manera.

\[\frac{|2 x-4|}{2}=\frac{|2 x-4|}{|2|}=\left|\frac{2 x-4}{2}\right|=|x-2|\]

Esta técnica es útil en varias situaciones. Por ejemplo, si quieres resolver la ecuación\(|2x − 4| = 6\), podrías dividir ambos lados por 2 y aplicar la propiedad cociente de los valores absolutos.

Distancia revisitada

Recordemos que para cualquier número real x, el valor absoluto de x se define como la distancia entre el número real x y el origen en la línea real. En esta sección, vamos a empujar un poco más este concepto de distancia.

Supongamos que tienes dos números reales en la línea real. Por ejemplo, en la figura que sigue, hemos localizado 3 y −2 en la línea real.

Se puede determinar la distancia entre los dos puntos restando el número de la izquierda del número de la derecha. Es decir, la distancia entre los dos puntos es d = 3 − (−2) = 5 unidades. Si restas en la otra dirección, obtienes el negativo de la distancia, como en −2 − 3 = −5 unidades. Por supuesto, la distancia es una cantidad no negativa, por lo que este resultado negativo no puede representar la distancia entre los dos puntos. En consecuencia, para encontrar la distancia entre dos puntos en la línea real, siempre se debe restar el número de la izquierda del número de la derecha.

Sin embargo, si tomas el valor absoluto de la diferencia, obtendrás el resultado correcto independientemente de la dirección de la resta.

\[d=|3-(-2)|=|5|=5 \quad \text { and } \quad d=|-2-3|=|-5|=5\]

Esta discusión lleva a la siguiente idea clave.

Propiedad 16.

Supongamos que a y b son dos números en la línea real

Se puede determinar la distancia d entre a y b en la línea real tomando el valor absoluto de su diferencia. Es decir,

\[d=|a-b|\]

Por supuesto, podrías restar en la otra dirección, obteniendo\(d = |b − a|\). Esto también es correcto.

Ahora que se ha introducido esta geometría de distancia, es útil pronunciar el simbolismo |a−b| como “la distancia entre a y b” en lugar de decir “el valor absoluto de a menos b”.

Ejemplo\(\PageIndex{10}\)

Resuelve la ecuación\[|x − 3| = 8\] para x.

Solución

Aquí está la situación ideal para aplicar nuestro nuevo concepto de distancia. En lugar de decir “el valor absoluto de x menos 3 es 8”, pronunciamos la ecuación\(|x − 3| = 8\) como “la distancia entre x y 3 es 8”.

Dibuja una recta numérica y localiza el número 3 en la línea.

Recordemos que la “distancia entre x y 3 es 8”. Dicho esto, marcar dos puntos en la línea real que están a 8 unidades de distancia de 3.

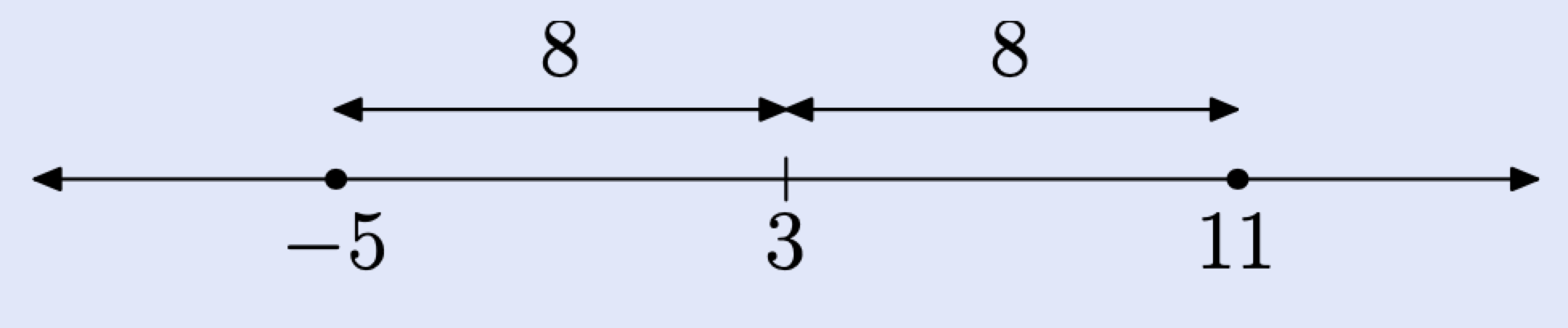
Así, las soluciones de |x − 3| = 8 son x = −5 o x = 11

Ejemplo\(\PageIndex{11}\)

Resuelve la ecuación\[|x + 5| = 2\] para x.

Solución

Reescribir la ecuación como diferencia. \[|x − (−5)| = 2\]Esto se pronuncia “la distancia entre x y −5 es 2". Localice dos puntos en la recta numérica que estén a 2 unidades de −5.

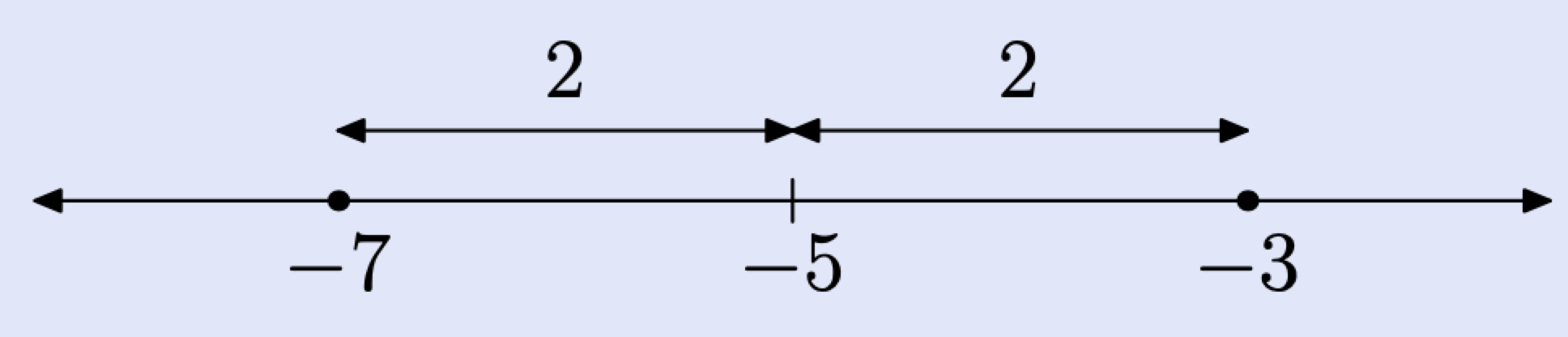
De ahí que las soluciones de\(|x + 5| = 2\) son x = −7 o x = −3.

Ejercicio

Para cada una de las ecuaciones de los Ejercicios 1 - 4, realice cada una de las siguientes tareas.

1. Configure un sistema de coordenadas en una hoja de papel cuadrilátero. Etiquetar y escalar cada eje.
2. Dibuje la gráfica de cada lado de la ecuación sin la ayuda de una calculadora. Etiquete cada gráfica con su ecuación.
3. Sombrear la solución de la ecuación en el eje x (si la hay) como se muestra en la Figura 5 (léase “Expectativas”) en la narrativa. Es decir, suelte líneas discontinuas desde los puntos de intersección hasta el eje, luego sombree y etiquete el conjunto de soluciones en el eje x.

Ejercicio\(\PageIndex{1}\)

|x| = −2

Contestar

Sin soluciones.

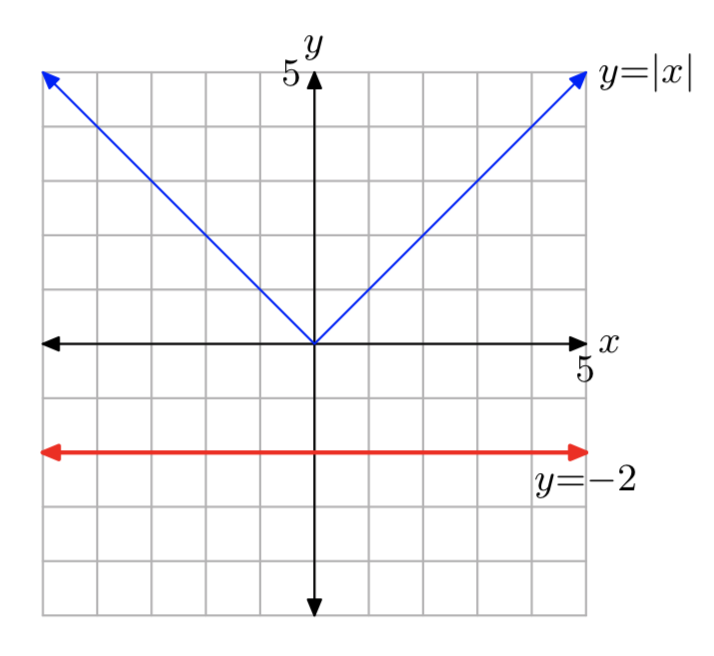
Ejercicio\(\PageIndex{2}\)

|x| = 0

Ejercicio\(\PageIndex{3}\)

|x| = 3

Contestar

Solución: x = −3 o x = 3.

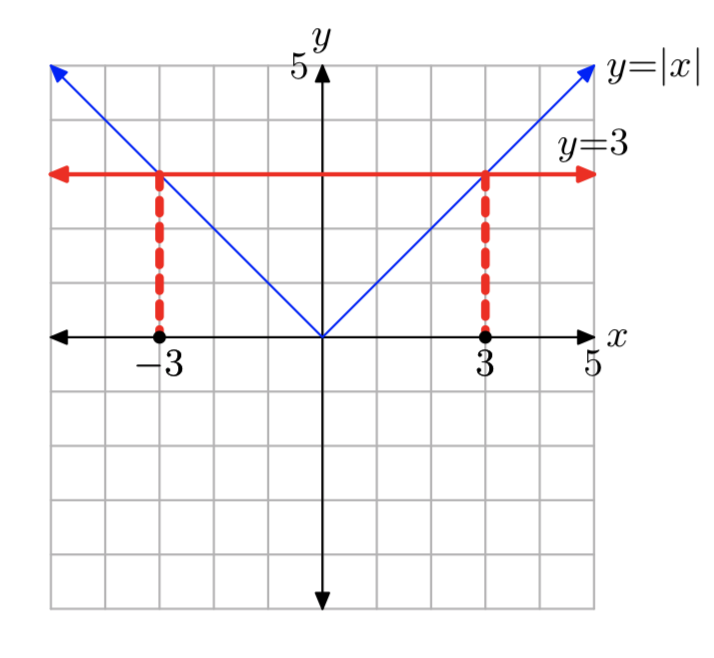
Ejercicio\(\PageIndex{4}\)

|x| = 2

Para cada una de las ecuaciones de los Ejercicios 5 - 8, realice cada una de las siguientes tareas.

1. Cargue cada lado de la ecuación en el menú Y= de su calculadora. Anuncio- solo la ventana de visualización para que todos los puntos de intersección de las dos gráficas sean visibles en la ventana de visualización.
2. Copia la imagen en tu pantalla de visualización en tu papel de tarea. Etiquete cada eje y escale cada eje con xmin, xmax, ymin e ymax. Etiquete cada gráfica con su ecuación.
3. Utilice la utilidad Intersect en el menú CALC para determinar los puntos de intersección. Sombra y etiquete cada solución como se muestra en la Figura 5 (léase “Expectativas”) en la narrativa. Es decir, suelte líneas discontinuas desde los puntos de intersección hasta el eje, luego sombree y etiquete el conjunto de soluciones en el eje x.

Ejercicio\(\PageIndex{5}\)

|3−2x| = 5

Contestar

Soluciones: x = −1 o x = 4.

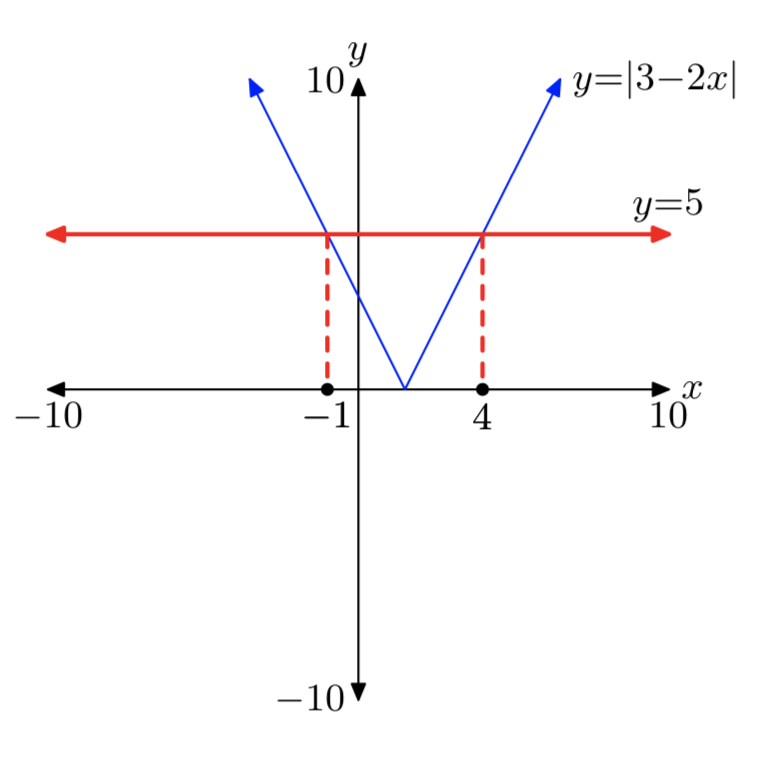
Ejercicio\(\PageIndex{6}\)

|2x+7| = 4

Ejercicio\(\PageIndex{7}\)

|4x+5| = 7

Contestar

Soluciones: x = −3 o x = 0.5.

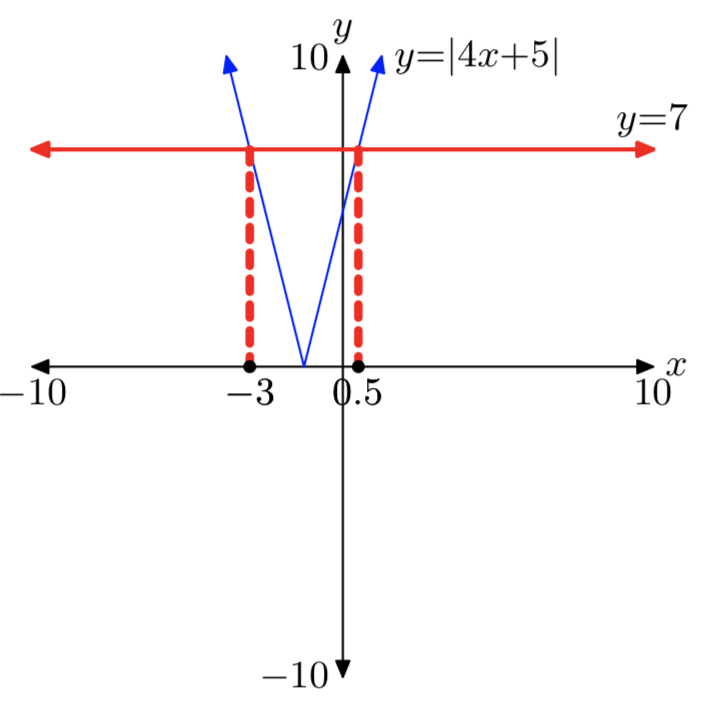
Ejercicio\(\PageIndex{8}\)

|5x−7| = 8

Para cada una de las ecuaciones en los Ejercicios 9 - 14, proporcionar una solución puramente algebraica sin el uso de una calculadora. Organice su trabajo como se muestra en los Ejemplos 6, 7 y 8 en la narrativa, pero no use una calculadora.

Ejercicio\(\PageIndex{9}\)

|4x+3| = 0

Contestar

\(x = −\frac{3}{4}\)

Ejercicio\(\PageIndex{10}\)

|3x−11| = −5

Ejercicio\(\PageIndex{11}\)

|2x+7| = 14

Contestar

\(x = −\frac{21}{2}\)o\(x = \frac{7}{2}\)

Ejercicio\(\PageIndex{12}\)

|7−4x| = 8

Ejercicio\(\PageIndex{13}\)

|3−2x| = −1

Contestar

Sin soluciones.

Ejercicio\(\PageIndex{14}\)

|4x+9| = 0

Para cada una de las ecuaciones de los Ejercicios 15 - 20, realice cada una de las siguientes tareas.

1. Organice cada una de las siguientes partes en su papel de tarea en la misma ubicación. No coloques la obra algebraica en una página y la obra gráfica en otra.
2. Siga cada una de las instrucciones dadas para los Ejercicios 5 - 8 para encontrar y registrar una solución con su calculadora gráfica.
3. Proporcione una solución puramente algebraica, mostrando todos los pasos de su trabajo. ¿Estas soluciones se comparan favorablemente con las que se encuentran usando su calculadora gráfica en la parte (ii)? Si no, busca un error en tu trabajo.

Ejercicio\(\PageIndex{15}\)

|x−8| = 7

Contestar

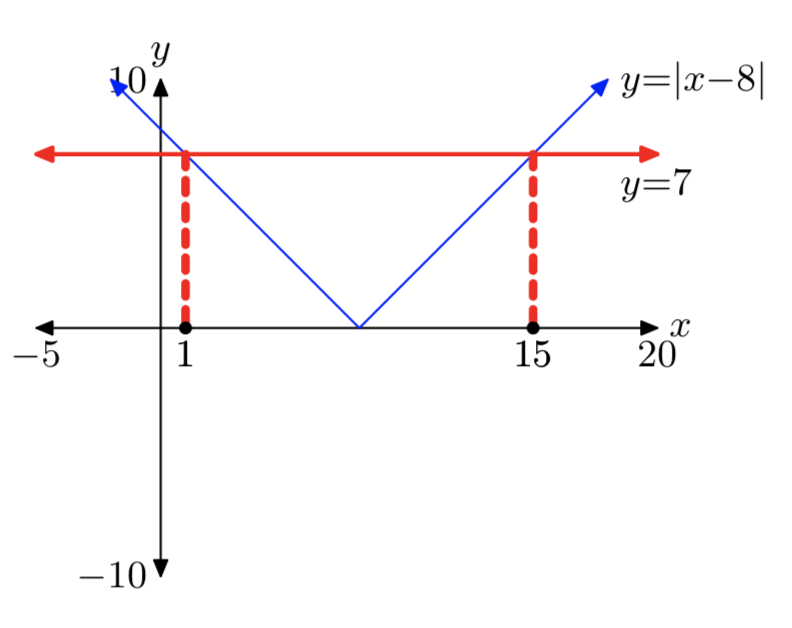
x = 1 o x = 15

Ejercicio\(\PageIndex{16}\)

|2x−15| = 5

Ejercicio\(\PageIndex{17}\)

|2x+11| = 6

Contestar

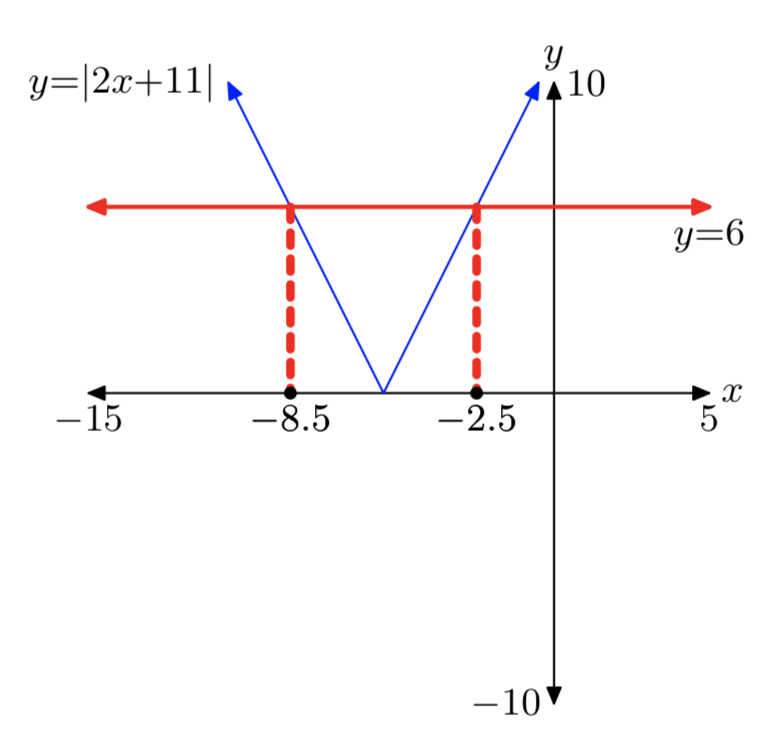
x = −8.5 o x = −2.5

Ejercicio\(\PageIndex{18}\)

|5x−21| = 7

Ejercicio\(\PageIndex{19}\)

|x−12| = 6

Contestar

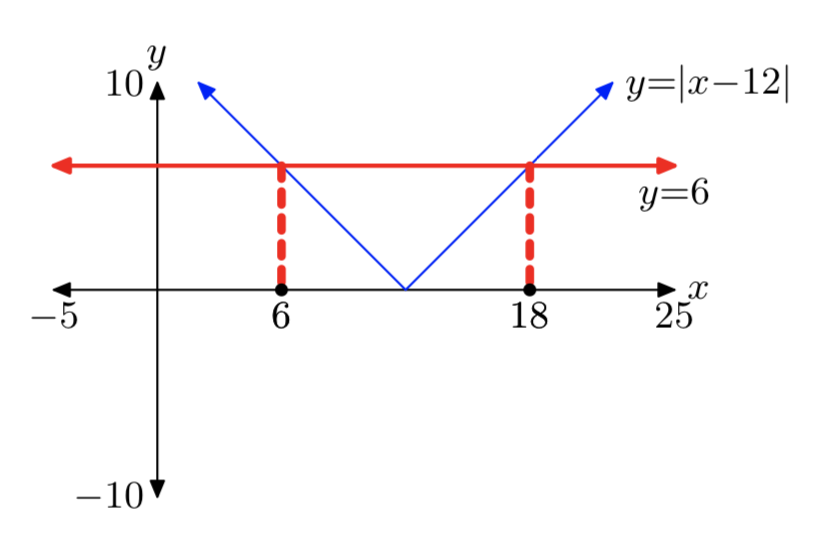
x = 6 o x = 18

Ejercicio\(\PageIndex{20}\)

|x+11| = 5

Utilizar una técnica estrictamente algebraica para resolver cada una de las ecuaciones en los Ejercicios 21 - 28. No utilice una calculadora.

Ejercicio\(\PageIndex{21}\)

|x+2|−3 = 4

Contestar

x = −9 o x = 5

Ejercicio\(\PageIndex{22}\)

3|x+5| = 6

Ejercicio\(\PageIndex{23}\)

−2|3−2x| = −6

Contestar

x = 0 o x = 3

Ejercicio\(\PageIndex{24}\)

|4−x|+5 = 12

Ejercicio\(\PageIndex{25}\)

3|x+2|−5 = |x+2|+7

Contestar

x = −8 o x = 4

Ejercicio\(\PageIndex{26}\)

4−3|4−x| = 2|4−x|−1

Ejercicio\(\PageIndex{27}\)

\(|\frac{x}{3}−\frac{1}{4}| = \frac{1}{12}\)

Contestar

\(x = \frac{1}{2}\)o x = 1

Ejercicio\(\PageIndex{28}\)

\(|\frac{x}{4}−\frac{1}{2}| = \frac{2}{3}\)

Utilizar la técnica de distancia en la recta numérica demostrada en los Ejemplos 16 y 17 para resolver cada una de las ecuaciones en los Ejercicios 29 - 32. Proporcione bocetos de líneas numéricas en su papel de tarea como se muestra en los Ejemplos 16 y 17 de la narrativa.

Ejercicio\(\PageIndex{29}\)

|x−5| = 8

Contestar

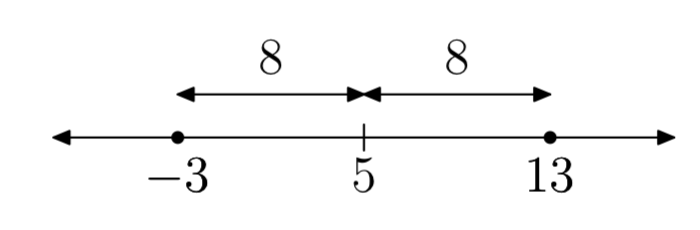
x = −3 o x = 13

Ejercicio\(\PageIndex{30}\)

|x−2| = 4

Ejercicio\(\PageIndex{31}\)

|x+4| = 3

Contestar

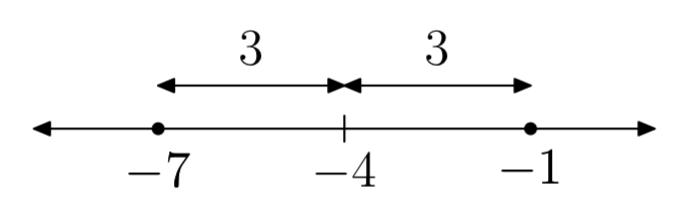
x = −7 o x = −1

Ejercicio\(\PageIndex{32}\)

|x+2| = 11

Usa las instrucciones proporcionadas en los Ejercicios 5 - 8 para resolver las ecuaciones en los Ejercicios 33 - 34.

Ejercicio\(\PageIndex{33}\)

\(|x+2| = \frac{1}{3}x+5\)

Contestar

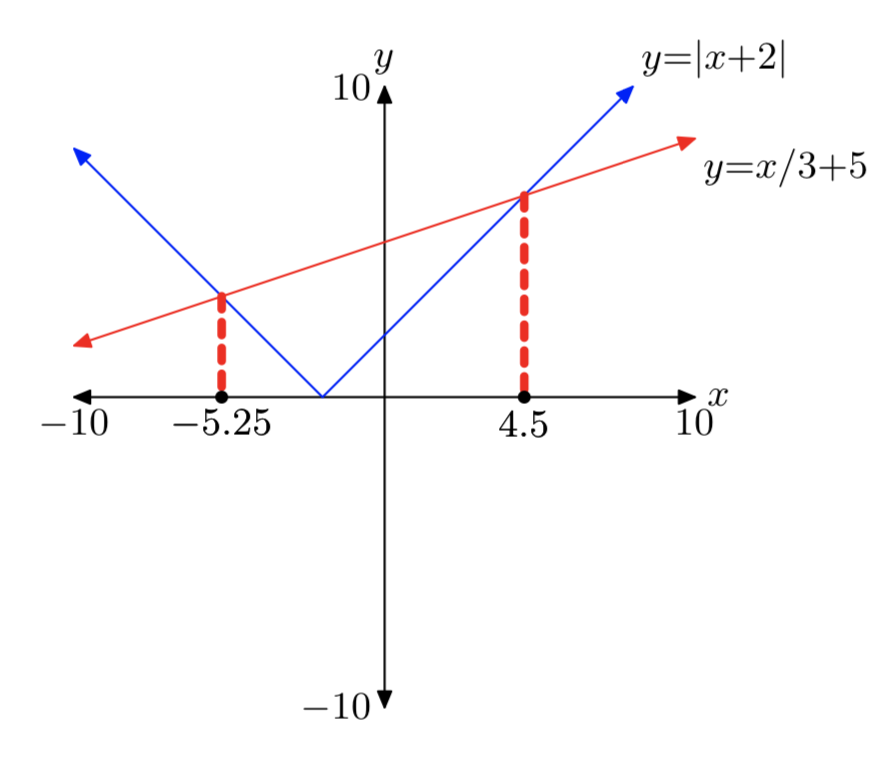
Ejercicio\(\PageIndex{34}\)

\(|x−3|=5−\frac{1}{2}x\)

En los Ejercicios 35 - 36, realice cada una de las siguientes tareas.

1. Configure un sistema de coordenadas en papel cuadrilátero. Etiquetar y escalar cada eje.
2. Sin el uso de una calculadora, dibuje los gráficos de los lados izquierdo y derecho de la ecuación dada. Etiquete cada gráfica con su ecuación.
3. Suelte líneas verticales discontinuas desde cada punto de intersección hasta el eje x. Sombra y etiquete cada solución en el eje x (tendrá que aproximarse).

Ejercicio\(\PageIndex{35}\)

\(|x−2| = \frac{1}{3}x+2\)

Contestar

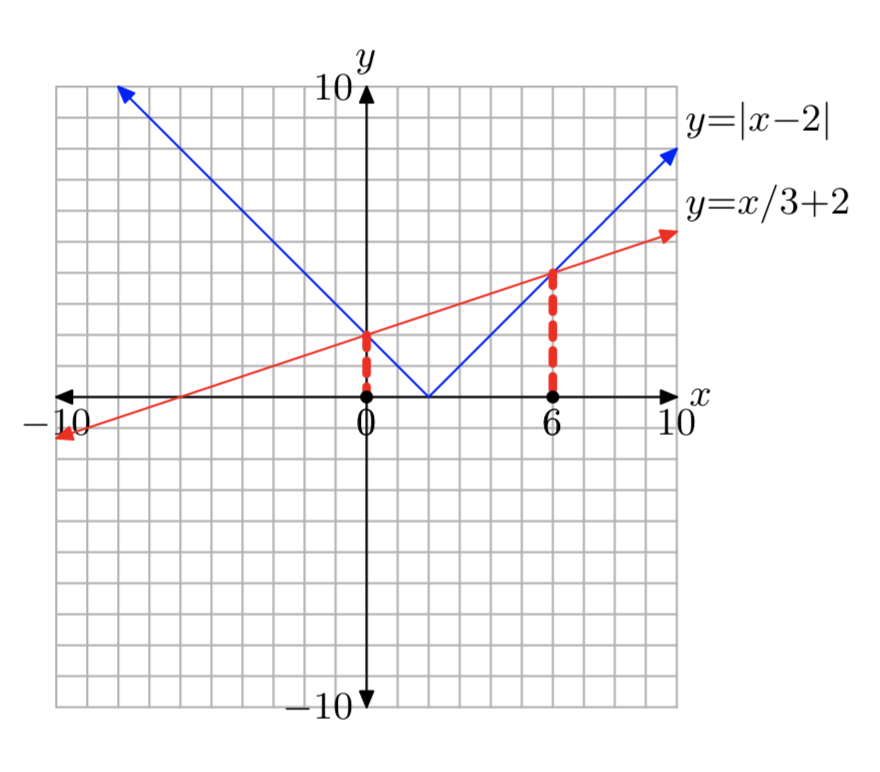
Ejercicio\(\PageIndex{36}\)

\(|x+4| = \frac{1}{3}x+4\)

Ejercicio\(\PageIndex{37}\)

Dado que un < 0 and b > 0, demostrar que |ab| = |a||b|.

Contestar

Si a es un número real negativo y b es un número real positivo, entonces ab es negativo, entonces |ab| = −ab. Por otro lado, un negativo también significa que |a| = −a, y b positivo significa que |b| = b, de modo que |a||b| = −a (b) = −ab. Al comparar estos resultados, vemos que |ab| y |a|b| igualan lo mismo, y así deben ser iguales entre sí.

Ejercicio\(\PageIndex{38}\)

Dado que a>0 y b<0, prueban que |ab| = |a||b|.

Ejercicio\(\PageIndex{39}\)

En la narrativa, probamos que si a > 0 y b < 0, entonces\(|\frac{a}{b}| = \frac{|a|}{|b|}\). Demostrar los tres casos restantes.

Contestar

CaseI. (a, b > 0) Si a y b son ambos números reales positivos, entonces\(\frac{a}{b}\) es positivo y así\(|\frac{a}{b}| = \frac{a}{b}\). Por otro lado, un positivo también significa que |a| = a, y b positivo significa que |b| = b, así que eso\(\frac{|a|}{|b|} = \frac{a}{b}\). Comparando estos dos resultados, vemos eso\(|\frac{a}{b}|\) e\(\frac{|a|}{|b|}\) igualan lo mismo, y así deben ser iguales entre sí.

Caso II. (a, b < 0) Si a y b son ambos números reales negativos, entonces\(\frac{a}{b}\) es positivo y así\(|\frac{a}{b}| = \frac{a}{b}\). Por otro lado, un negativo también significa que |a| = −a, y b negativo significa que |b| = −b, así que eso\(\frac{|a|}{|b|} = \frac{−a}{(−b)} = \frac{a}{b}\). Comparando estos dos resultados, vemos eso\(|\frac{a}{b}|\) e\(\frac{|a|}{|b|}\) igualan lo mismo, y así deben ser iguales entre sí.

Caso III. (a < 0, b > 0) Si a es un número real negativo y b es un número real positivo, entonces\(\frac{a}{b}\) es negativo y así\(|\frac{a}{b}| =−(\frac{a}{b})\). Por otro lado, un negativo también significa que |a| = −a, y b positivo significa que |b| = b, así que eso\(\frac{|a|}{|b|} = −\frac{a}{b} = −(\frac{a}{b})\). Comparando estos dos resultados, vemos eso\(|\frac{a}{b}|\) e\(\frac{|a|}{|b|}\) igualan lo mismo, y así deben ser iguales entre sí.