8.5: Funciones logarítmicas
- Page ID
- 110688
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Ahora podemos aplicar la teoría de la función inversa de la sección anterior a la función exponencial. De la Sección 8.2, sabemos que la función\(f(x) = b^x\) está aumentando (si b > 1) o decreciente (si 0 < b < 1), y por lo tanto es uno a uno. En consecuencia, f tiene una función inversa\(f^{−1}\).
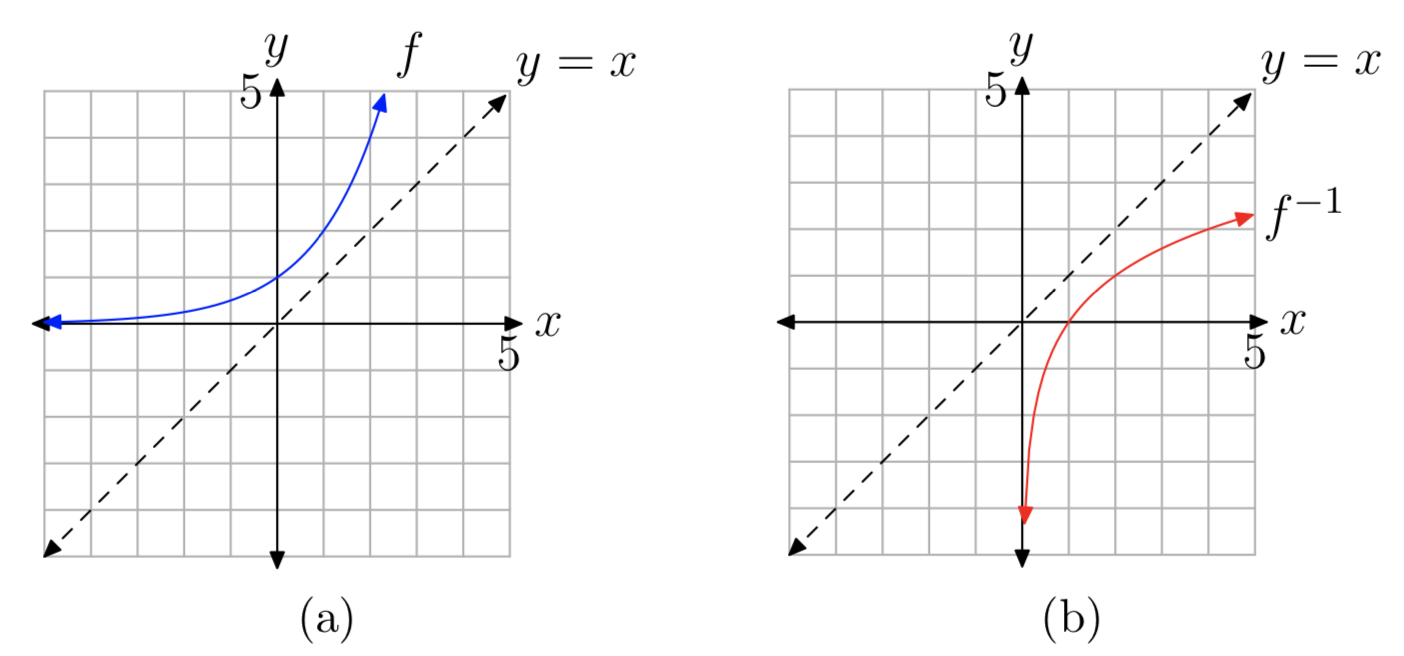
Como ejemplo, consideremos la función exponencial\(f(x) = 2^x\). f está aumentando, tiene dominio\(D_{f} = (−\infty, \infty)\) y rango\(R_{f} = (0, \infty)\). Su gráfica se muestra en la Figura 1 (a). El gráfico de la función inversa\(f^{−1}\) es un reflejo de la gráfica de f a través de la línea y = x, y se muestra en la Figura 1 (b). Dado que los dominios y rangos se intercambian, el dominio de la función inversa es\(D_{f^{−1}} = (0, \infty)\) y el rango es\(R_{f^{−1}} = (−\infty, \infty)\).
Desafortunadamente, cuando tratamos de utilizar el procedimiento dado en la Sección 8.4 para encontrar una fórmula para\(f^{−1}\), nos encontramos con un problema. Comenzando con\(y = 2^x\), luego intercambiamos x e y para obtener\(x = 2^y\). Pero ahora no tenemos ningún método algebraico para resolver esta última ecuación para y Se deduce que la inversa de no\(f(x) = 2^x\) tiene ninguna fórmula que involucre las operaciones aritméticas habituales y las funciones con las que estamos familiarizados. Así, la función inversa es una función nueva. El nombre de esta nueva función es el logaritmo de x a base 2, y se denota por\(f^{−1}(x) = log_{2}(x)\).
Recordemos que la relación definitoria entre una función y su inversa (Propiedad 14 en la Sección 8.4) simplemente establece que las entradas y salidas de las dos funciones son intercambiadas. Así, la relación entre\(2^x\) y su inversa\(log_{2}(x)\) toma la siguiente forma:
\(v = log_{2}(u) \longleftrightarrow u = 2^v\)
De manera más general, para cada función exponencial\(f(x) = b^x\) (b > 0,\(b \ne 1\)), la función inversa\(f^{−1}(x)\) se denomina logaritmo de x a base b, y se denota por\(log_{b}(x)\). La relación definitoria se da en la siguiente definición.
Definición\(\PageIndex{1}\)
Si b > 0 y\(b \ne 1\), entonces el logaritmo de u a base b se define por la relación
\(v = log_{b}(u) \longleftrightarrow u = b^v\). (2)
Para entender mejor la función logaritmo, trabajemos a través de algunos ejemplos simples.
Ejemplo\(\PageIndex{3}\)
\(log_{2}(8)\)Cómplese.
- Contestar
-
Etiquetar el valor requerido por v, entonces\(v = log_{2}(8)\). Entonces por (2), usando b = 2 y u = 8, se deduce eso\(2^v = 8\), y por lo tanto v = 3 (resolviendo por inspección).
En el último ejemplo, tenga en cuenta que\(log_{2}(8) = 3\) is the exponent v tal que\(2^v = 8\). Así, en general, una manera de interpretar la definición del logaritmo en (2) es que\(log_{b}(u)\) es el exponente v tal que\(b^v = u\). En otras palabras, ¡el valor del logaritmo es el exponente!
Ejemplo\(\PageIndex{4}\)
\(log_{10}(10000)\)Cómplese.
- Contestar
-
Nuevamente, etiquetar el valor requerido por v, entonces\(v = log_{10}(10000)\). Por (2), se deduce que\(10^v = 10 000\), y por lo tanto v = 4. Tenga en cuenta que aquí nuevamente hemos encontrado el exponente v = 4 que se necesita para la base 10 para poder obtener\(10^v = 10 000\).
Ejemplo\(\PageIndex{5}\)
\(log_{3}(\frac{1}{9})\)Cómplese.
- Contestar
-
\(v = log_{3}(\frac{1}{9})\)
\(\rightarrow 3^v = \frac{1}{9}\)por (2)
\(\rightarrow v = −2\)desde\(3^{−2} = \frac{1}{9}\)
Ejemplo\(\PageIndex{6}\)
Resuelve la ecuación\(log_{5}(x) = 1\).
- Contestar
-
\(log_{5}(x) = 1\)
\(\rightarrow 5^1 = x\)por (2)
\(\rightarrow x = 5\)
Ejemplo\(\PageIndex{7}\)
Resuelve la ecuación\(log_{b}(64) = 3\) para b.
- Contestar
-
\(log_{b}(64) = 3\)
\(\rightarrow b^3 = 64\)por (2)
\(\rightarrow b = \sqrt[3]{64} = 4\)
Ejemplo\(\PageIndex{8}\)
Resuelve la ecuación\(log_{\frac{1}{2}}(x) = −2\).
- Contestar
-
\(log_{\frac{1}{2}}(x) = −2\)
\(\rightarrow (\frac{1}{2})^{−2} = x\)por (2)
\(\rightarrow \frac{1}{(\frac{1}{2})^2} = \frac{1}{\frac{1}{4}} = 4\)
Las relaciones de composición en el Bien 15 de la Sección 8.4, aplicadas a\(b^x\) y\(log_{b}(x)\), se convierten
PROPIEDAD\(\PageIndex{9}\)
\[log_{b}(b^x) = x \label{10}\]
y
\[b^{log_{b}(x)} = x \label{11}.\]
Ambas ecuaciones son importantes. Tenga en cuenta que Ecuatio n\ ref {11} ag ain muestra que el\(log_{b}(x)\) es el exponente v tal que\(b^v = x\). Equatio n\ ref {10} se utilizará frecuentemente en esta y posteriores secciones para ayudarnos a resolver ecuaciones exponenciales.
Las funciones logarítmicas se utilizan en muchas áreas de la ciencia y la ingeniería. Por ejemplo, se utilizan para definir la escala de Richter para las magnitudes de los terremotos, la escala de decibelios para la sonoridad del sonido y la escala astronómica para el brillo estelar. También son herramientas importantes para su uso en computación (como veremos en la Sección 8.8). Nuestro principal uso de logaritmos en este libro de texto será resolver ecuaciones exponenciales, y con ello ayudarnos a estudiar fenómenos físicos que son descritos por funciones exponenciales (como en la Sección 8.7).
Logaritmos de Computación
En los Ejemplos 3 — 8 anteriores, pudimos calcular los logaritmos mediante la conversión a ecuaciones exponenciales que podrían resolverse por inspección. Pero es fácil ver que la mayor parte del tiempo esto no va a funcionar. Por ejemplo, ¿cómo calcularíamos el valor de\(log_{2}(7)\)?
Afortunadamente, los matemáticos han encontrado otros métodos para computar logaritmos con alta precisión, y ahora se pueden aproximar fácilmente usando una calculadora o computadora.
Su calculadora tiene botones incorporados para computar dos logaritmos diferentes,\(log_{10}(x)\) y\(log_{e}(x)\). \(log_{10}(x)\)se llama logaritmo común, y\(log_{e}(x)\) se llama logaritmo natural.
Logaritmo Común: El logaritmo común\(log_{10}(x)\) se calcula usando el LogButton en su calculadora. Observe también que su función inversa\(10^x\), puede calcularse usando el mismo botón en conjunto con el botón 2ND. El logaritmo común suele ser el más conveniente de usar para cálculos que involucran notación científica (porque usamos un sistema numérico base 10), y por lo tanto es el logaritmo más utilizado en las ciencias físicas. Debido a eso, a menudo solo se abrevia por log (x), y lo haremos también en el resto del texto.
LOARITMO COMÚN
log (x) y\(log_{10}(x)\) son anotaciones equivalentes. Así, tenemos la relación definitoria
\(v = log(u) \longleftrightarrow u = 10^v\).
Las propiedades de composición para el logaritmo común son
\(log(10^x) = x\)(12)
y
\(10^{log(x)} = x\).
Logaritmo Natural: El logaritmo natural\(log_{e}(x)\) is computed using the LNbutton on your calculator. Its inverse function, \(e^x\), se calcula utilizando el mismo botón en conjunto con el botón 2ND. El logaritmo natural resulta ser el más conveniente de usar en matemáticas, porque muchas fórmulas, especialmente en el cálculo, son mucho más simples cuando se usa el logaritmo natural. El logaritmo natural es abreviado por ln (x).
LOARITMO NATURAL
ln (x) y\(log_{e}(x)\) son anotaciones equivalentes. Así, tenemos la relación definitoria
\(v = ln(u) \longleftrightarrow u = e^v\).
Las propiedades de composición para el logaritmo común son
\[ln(e^x) = x \label{13}\]
y
\[e^{\ln(x)} = x \lable{14}\]
Tenga en cuenta que al usar su calculadora para calcular log (x) y ln (x), generalmente solo obtendrá valores aproximados, ya que estos valores frecuentemente son números irracionales.
¿Qué pasa con otras bases? También puedes calcularlos en tu calculadora, pero primero necesitaremos desarrollar el Cambio de Fórmula Base en la siguiente sección. Sin embargo, en este punto, podemos al menos resolver ecuaciones exponenciales que involucran las bases 10 y e, como se muestra en los siguientes dos ejemplos.
Ejemplo\(\PageIndex{14}\)
Resuelve la ecuación\(704 = 2(10)^{x}\).
- Contestar
-
El primer paso es aislar lo exponencial en el lado derecho dividiendo ambos lados por 2:
\(352 = 10^x\)
Luego simplemente aplique la\(log_{10}(x)\) función a ambos lados de la ecuación:
\(log_{10}(352) = log_{10}(10^x)\)
Pero (10) eso implica\(log_{10}(10^x) = x\). Por lo tanto,\(x = log_{10}(352) = log(352)\) es la solución exacta. El valor aproximado, utilizando una calculadora, es 2.546542663 (ver Figura 2). Alternativamente, en lugar de tomar el logaritmo de ambos lados en el segundo paso, se puede aplicar (2) a la ecuación\(352 = 10^x\) para obtener\(x = log_{10}(352)\).
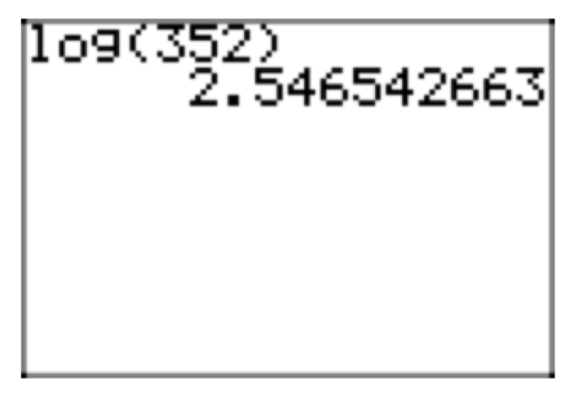
Figura 2. Aproximación de\(log(352) = log_{10}(352)\).
Este último ejemplo muestra cómo se pueden utilizar logaritmos para resolver ecuaciones exponenciales. La estrategia básica es aislar primero lo exponencial en un lado de la ecuación, y luego tomar logaritmos apropiados de ambos lados. Aquí hay un ejemplo más por ahora, y luego volveremos a este proceso repetidamente en las secciones restantes, especialmente cuando trabajamos con problemas de aplicación.
Ejemplo\(\PageIndex{15}\)
Resuelve la ecuación\(30 = 20e^x\).
- Contestar
-
Primero aísle el exponencial en el lado derecho dividiendo ambos lados por 20:
\(1.5 = e^x\)
Esta vez, dado que la base de la función exponencial es e, aplique la función logaritmo natural a ambos lados:
\(log_{e}(1.5) = log_{e}(e^x)\)
Simplifica el lado derecho, ya que\(log_{e}(e^x) = x\) por (10):
\(log_{e}(1.5) = x\)
Por lo tanto,\(x = log_{e}(1.5) = ln(1.5)\) es la solución exacta. El valor aproximado, utilizando una calculadora, es 0.4054651081 (ver Figura 3).
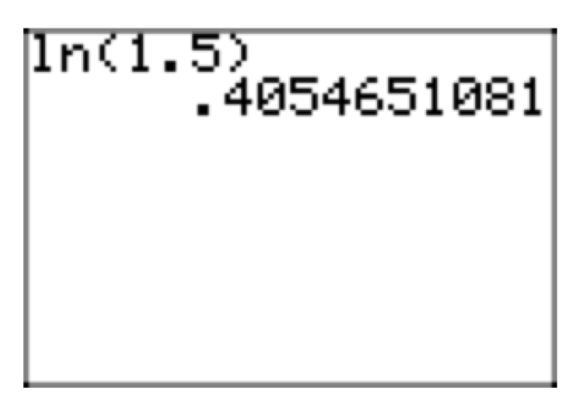
Figura 3. Aproximación de\(ln1.5 = log_{e}(1.5)\).
En la siguiente sección, aprenderemos a resolver ecuaciones exponenciales que involucran otras bases.
Gráficas de funciones logarítmicas
Al inicio de esta sección, observamos las gráficas de\(f(x) = 2^x\) y su función inversa\(f^{−1}(x) = log_{2}(x)\). De manera más general, la gráfica de la función exponencial\(f(x) = b^x\) para b > 1 se muestra en la Figura 4 (a), junto con su función logarítmica inversa\(f^{−1}(x) = log_{b}(x)\). De acuerdo con la Sección 8.4, las dos gráficas son reflexiones a través de la línea y = x Del mismo modo, la gráfica para 0 < b < 1 se muestra en la Figura 4 (b).
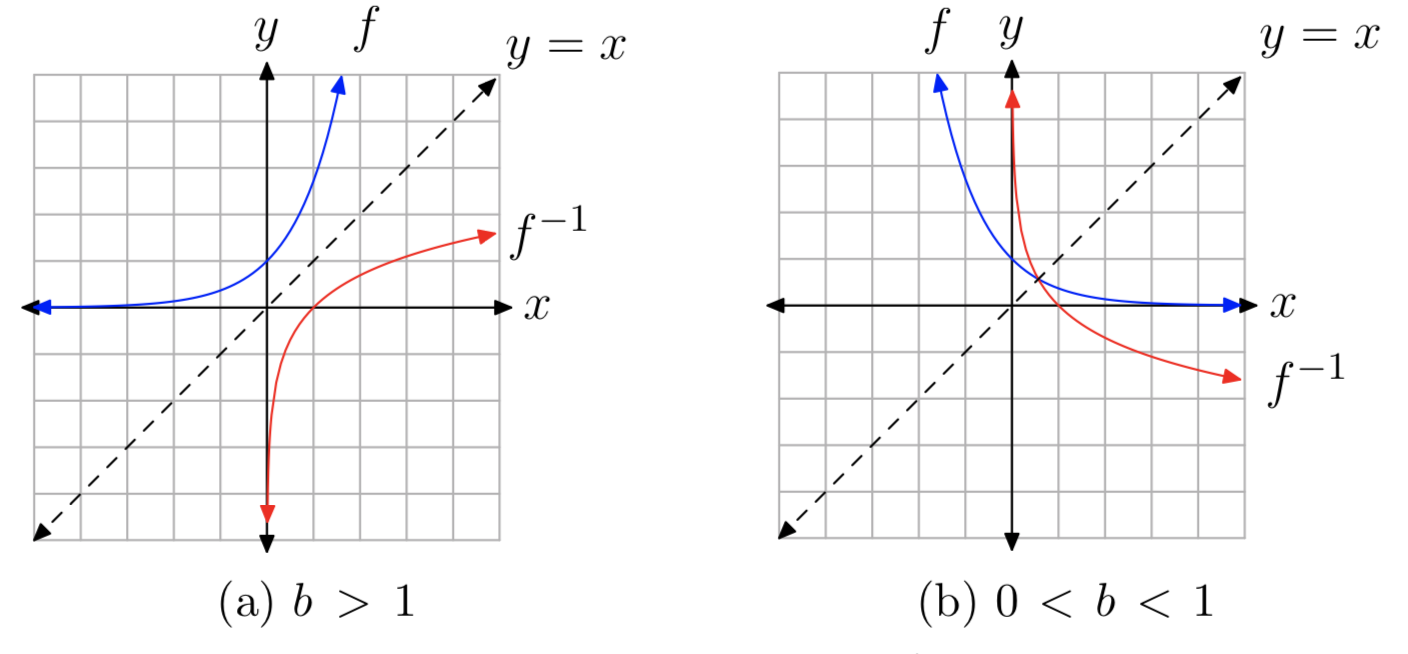
Debido a que se intercambian dominios y rangos de funciones inversas, se deduce que
PROPIEDAD\(\PageIndex{16}\)
\(Domain(log_{b}(x)) = (0, \infty)\)
y
\(Range(log_{b}(x)) = (−\infty, \infty)\).
En particular, señalar que el logaritmo de un número negativo, así como el logaritmo de 0, no están definidos.
Dos puntos particulares en la gráfica del logaritmo son dignos de mención. Ya que\(b^0 = 1\), se deduce que\(log_{b}(1) = 0\), y por lo tanto la intersección x de la gráfica de\(log_{b}(x)\) es (1, 0). De igual manera\(b^1 = b\), ya que, se deduce que\(log_{b}(b) = 1\), y por lo tanto (b, 1) está en la gráfica.
PROPIEDAD\(\PageIndex{17}\)
\(log_{b}(1) = 0\)
y
\(log_{b}(b) = 1\)
Finalmente, dado que la gráfica de\(b^x\) tiene una asíntota horizontal y = 0, la gráfica de\(log_{b}(x)\) debe tener una asíntota vertical x = 0. Este comportamiento es consecuencia de que se intercambian entradas y salidas de funciones inversas, y se puede observar en la Figura 4.
En el ejemplo final a continuación, aplicaremos una transformación al logaritmo y veremos cómo eso afecta a la gráfica.
Ejemplo\(\PageIndex{18}\)
Trazar la gráfica de la función\(f(x) = log_{2}(x+1)\).
- Contestar
-
La gráfica de\(f(x) = log_{2}(x+1)\) será la misma que la gráfica de\(g(x) = log_{2}(x)\) desplazada una unidad a la izquierda. La gráfica de g se muestra en la Figura 1 (b). La intercepción x (1, 0) en la gráfica de g se desplazará una unidad a la izquierda a (0,0) en la gráfica de f. Asimismo, la asíntota vertical x = 0 en la gráfica de g se desplazará una unidad a la izquierda a la línea x = −1 en la gráfica de f. La gráfica final de f se muestra en la Figura 5.
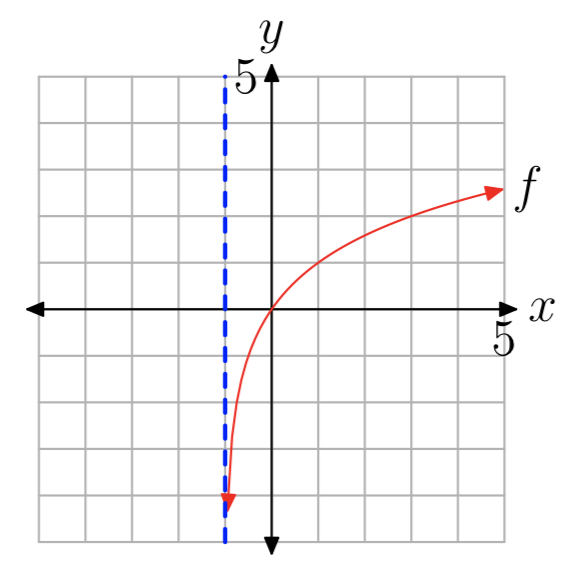
Figura 5. La gráfica de\(f(x) = log_{2}(x+1)\).
Ejercicio
En Ejercicios 1 - 18, encuentra el valor exacto de la función en el valor dado b.
Ejercicio\(\PageIndex{1}\)
\(f(x) = log_{3}(x)\);\(b = \sqrt[5]{3}\).
- Contestar
-
\(\frac{1}{5}\)
Ejercicio\(\PageIndex{2}\)
\(f(x) = log_{5}(x)\); b = 3125.
Ejercicio\(\PageIndex{3}\)
\(f(x) = log_{2}(x)\);\(b = \frac{1}{16}\).
- Contestar
-
−4
Ejercicio\(\PageIndex{4}\)
\(f(x) = log_{2}(x)\); b = 4.
Ejercicio\(\PageIndex{5}\)
\(f(x) = log_{5}(x)\); b = 5.
- Contestar
-
1
Ejercicio\(\PageIndex{6}\)
\(f(x) = log_{2}(x)\); b = 8.
Ejercicio\(\PageIndex{7}\)
\(f(x) = log_{2}(x)\); b = 32.
- Contestar
-
5
Ejercicio\(\PageIndex{8}\)
\(f(x) = log_{4}(x)\);\(b = \frac{1}{16}\).
Ejercicio\(\PageIndex{9}\)
\(f(x) = log_{5}(x)\);\(b = \frac{1}{3125}\).
- Contestar
-
−5
Ejercicio\(\PageIndex{10}\)
\(f(x) = log_{5}(x)\);\(b = \frac{1}{25}\).
Ejercicio\(\PageIndex{11}\)
\(f(x) = log_{5}(x)\);\(b = \sqrt[6]{5}\).
- Contestar
-
\(\frac{1}{6}\)
Ejercicio\(\PageIndex{12}\)
\(f(x) = log_{3}(x)\);\(b = \sqrt[3]{3}\).
Ejercicio\(\PageIndex{13}\)
\(f(x) = log_{6}(x)\);\(b = \sqrt[6]{6}\).
- Contestar
-
\(\frac{1}{6}\)
Ejercicio\(\PageIndex{14}\)
\(f(x) = log_{5}(x)\);\(b = \sqrt[5]{5}\).
Ejercicio\(\PageIndex{15}\)
\(f(x) = log_{2}(x)\);\(b = \sqrt[6]{2}\).
- Contestar
-
\(\frac{1}{6}\)
Ejercicio\(\PageIndex{16}\)
\(f(x) = log_{4}(x)\);\(b = \frac{1}{4}\).
Ejercicio\(\PageIndex{17}\)
\(f(x) = log_{3}(x)\);\(b = \frac{1}{9}\).
- Contestar
-
−2
Ejercicio\(\PageIndex{18}\)
\(f(x) = log_{4}(x)\); b = 64.
En Ejercicios 19 - 26, utilice una calculadora para evaluar la función al valor dado p. Redondee su respuesta a la centésima más cercana.
Ejercicio\(\PageIndex{19}\)
f (x) = ln (x); p = 10.06.
- Contestar
-
2. 31
Ejercicio\(\PageIndex{20}\)
f (x) = ln (x); p = 9.87.
Ejercicio\(\PageIndex{21}\)
f (x) = ln (x); p = 2.40.
- Contestar
-
0.88
Ejercicio\(\PageIndex{22}\)
f (x) = ln (x); p = 9.30.
Ejercicio\(\PageIndex{23}\)
f (x) = log (x); p = 7.68.
- Contestar
-
0.89
Ejercicio\(\PageIndex{24}\)
f (x) = log (x); p = 652.22.
Ejercicio\(\PageIndex{25}\)
f (x) = log (x); p = 6.47.
- Contestar
-
0.81
Ejercicio\(\PageIndex{26}\)
f (x) = log (x); p = 86.19.
En los Ejercicios 27 - 34, resuelve la ecuación dada, y redondear tu respuesta a la centésima más cercana.
Ejercicio\(\PageIndex{27}\)
\(13 = e^{8x}\)
- Contestar
-
0.32
Ejercicio\(\PageIndex{28}\)
\(2 = 8e^{x}\)
Ejercicio\(\PageIndex{29}\)
\(19 = 10^{8x}\)
- Contestar
-
0.16
Ejercicio\(\PageIndex{30}\)
\(17 = 10^{2x}\)
Ejercicio\(\PageIndex{31}\)
\(7 = 6(10)^{x}\)
- Contestar
-
0.07
Ejercicio\(\PageIndex{32}\)
\(7 = e^{9x}\)
Ejercicio\(\PageIndex{33}\)
\(13 = 8e^{x}\)
- Contestar
-
0.49
Ejercicio\(\PageIndex{34}\)
\(5 = 7(10)^{x}\)
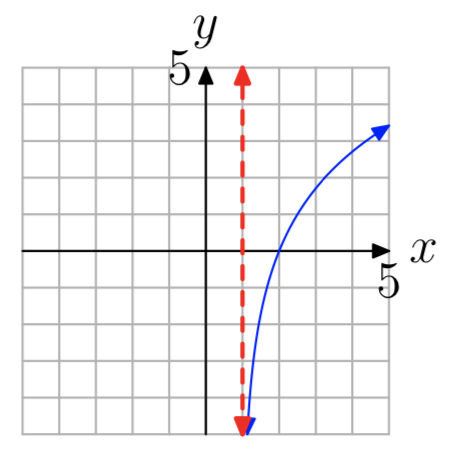
En los Ejercicios 35 - 42 se muestra la gráfica de una función logarítmica de\(f(x) = log_{b}(x−a)\) la forma. La línea roja discontinua es una asíntota vertical. Determinar el dominio de la función. Exprese su respuesta en notación de intervalos.
Ejercicio\(\PageIndex{35}\)
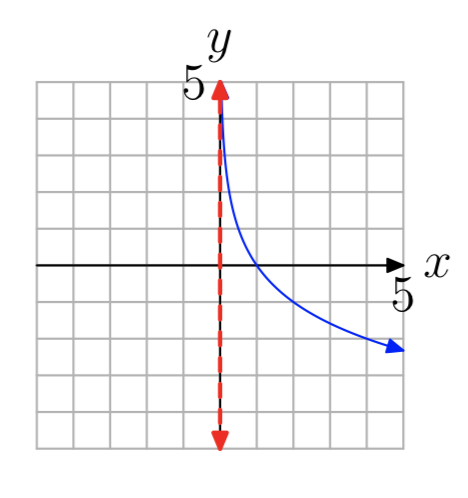
- Contestar
-
\((0, \infty)\)
Ejercicio\(\PageIndex{36}\)
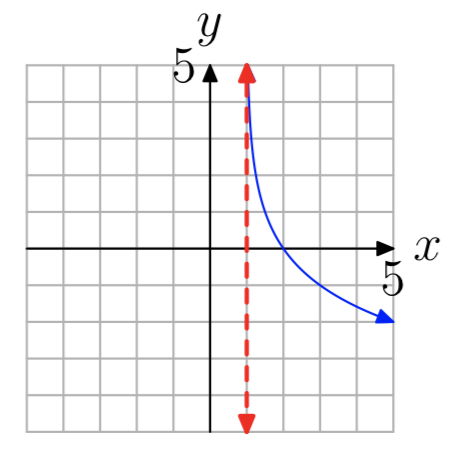
Ejercicio\(\PageIndex{37}\)
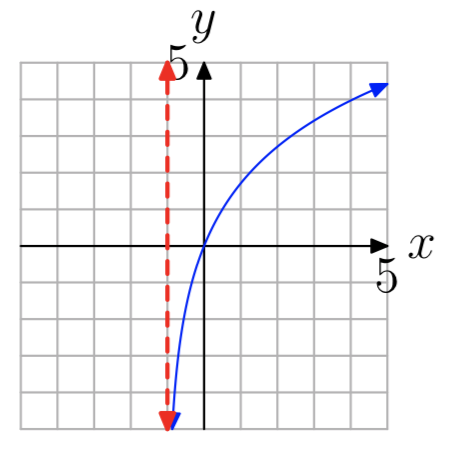
- Contestar
-
\((−1, \infty)\)
Ejercicio\(\PageIndex{38}\)
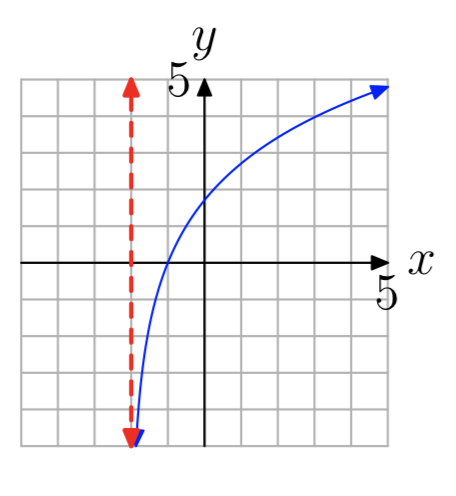
Ejercicio\(\PageIndex{39}\)
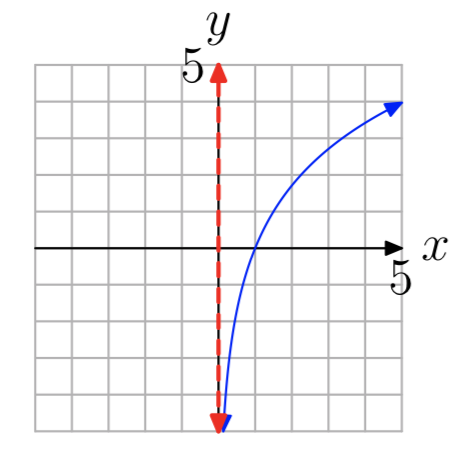
- Contestar
-
\((0, \infty)\)
Ejercicio\(\PageIndex{40}\)
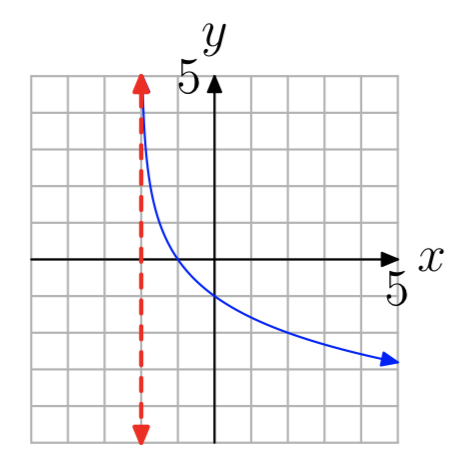
Ejercicio\(\PageIndex{41}\)
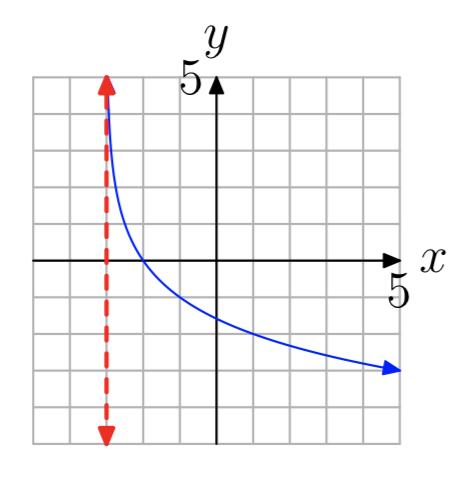
- Contestar
-
\((−3, \infty)\)
Ejercicio\(\PageIndex{42}\)