9.3: Propiedades de división de los radicales
- Page ID
- 110702
Cada una de las ecuaciones\(x^2 = a\) y\(x^2 = b\) tiene una solución positiva única,\(x = \sqrt{a}\) y\(x =\sqrt{b}\), respectivamente, proporcionan\(a\) y\(b\) son números reales positivos. Además, debido a que son soluciones, pueden ser sustituidas en las ecuaciones\(x^2 = a\) y\(x^2 = b\) para producir los resultados
\((\sqrt{a})^2 = a\)y\((\sqrt{b})^2 =b\),
respectivamente. Estos resultados dependen del hecho de que a y b son números reales positivos.
Del mismo modo, la ecuación
\[x^2 = \frac{a}{b} \nonumber\]
tiene la solución positiva única
\[x = \sqrt{\frac{a}{b}} \nonumber\]
siempre\(a\) y\(b\) son números reales positivos. Sin embargo, tenga en cuenta que
\[\left(\frac{\sqrt{a}}{\sqrt{b}}\right)^2 = \frac{(\sqrt{a})^2}{(\sqrt{b})^2} = \frac{a}{b}, \nonumber \]
haciendo\(\frac{\sqrt{a}}{\sqrt{b}}\) una segunda solución positiva de\(x^2 = \frac{a}{b}\). Sin embargo, debido a que\(\sqrt{\frac{a}{b}}\) es la única solución positiva de\(x^2 = \frac{a}{b}\), esto obliga
\[\sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}} \nonumber\]
Esta discusión nos lleva a la siguiente propiedad de los radicales.
Propiedad 1
Dejar\(a\) y\(b\) ser números reales positivos. Entonces,
\[\sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}}\]
Este resultado se puede utilizar de dos maneras claramente diferentes.
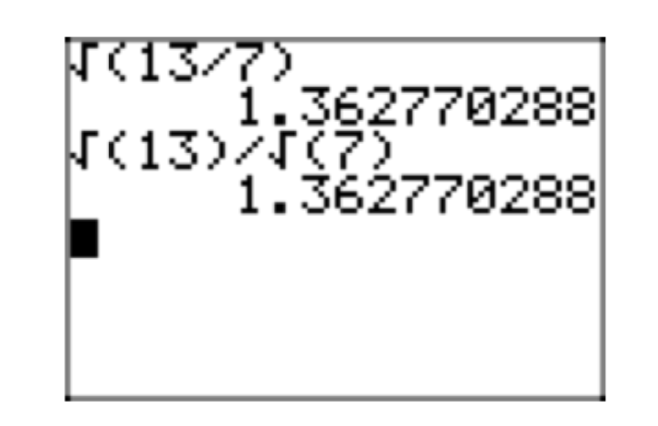
- Puedes usar el resultado para dividir dos raíces cuadradas, como en\[\frac{\sqrt{13}}{\sqrt{7}} = \sqrt{\frac{13}{7}} \nonumber\]
- También puedes usar el resultado para tomar la raíz cuadrada de una fracción. Simplemente tome la raíz cuadrada tanto del numerador como del denominador, como en\[\sqrt{\frac{13}{7}} = \frac{\sqrt{13}}{\sqrt{7}} \nonumber\]
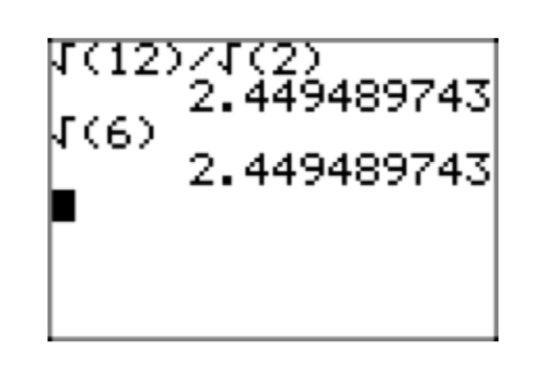
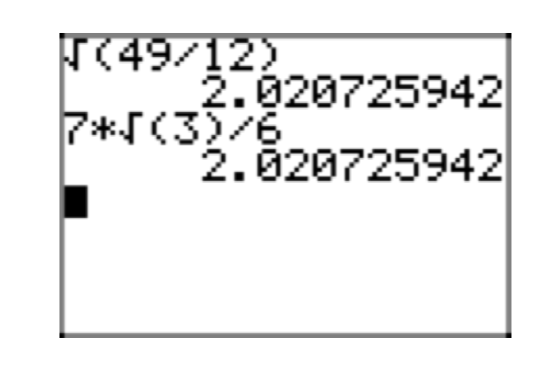
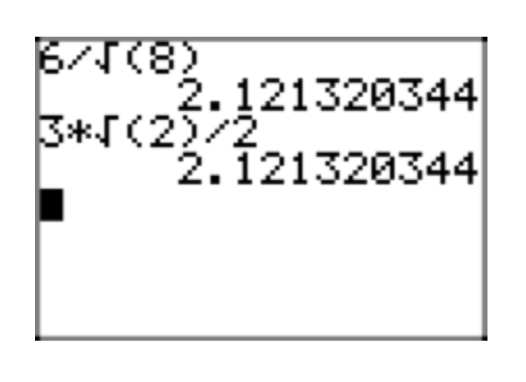
Es interesante verificar estos resultados en una calculadora, como se muestra en la Figura 1.
Continuación de la forma radical simple
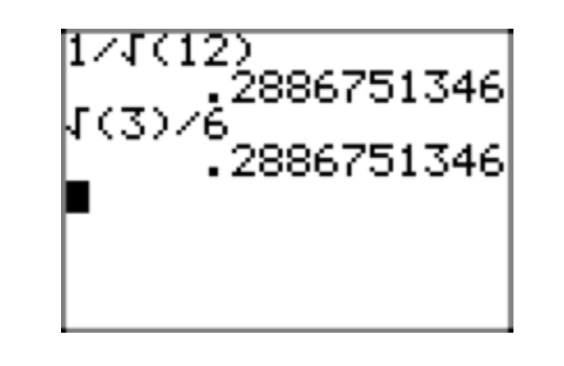
David y Martha vuelven a trabajar en un problema con la tarea. Martha obtiene la solución\(\sqrt{\frac{1}{12}}\), pero la solución de David\(\frac{1}{(2\sqrt{3})}\) es aparentemente diferente. Habiendo aprendido su lección en una tarea anterior, utilizan sus calculadoras para encontrar aproximaciones decimales de sus soluciones. La aproximación de Martha se muestra en la Figura 2 (a) y la aproximación de David se muestra en la Figura 2 (b).
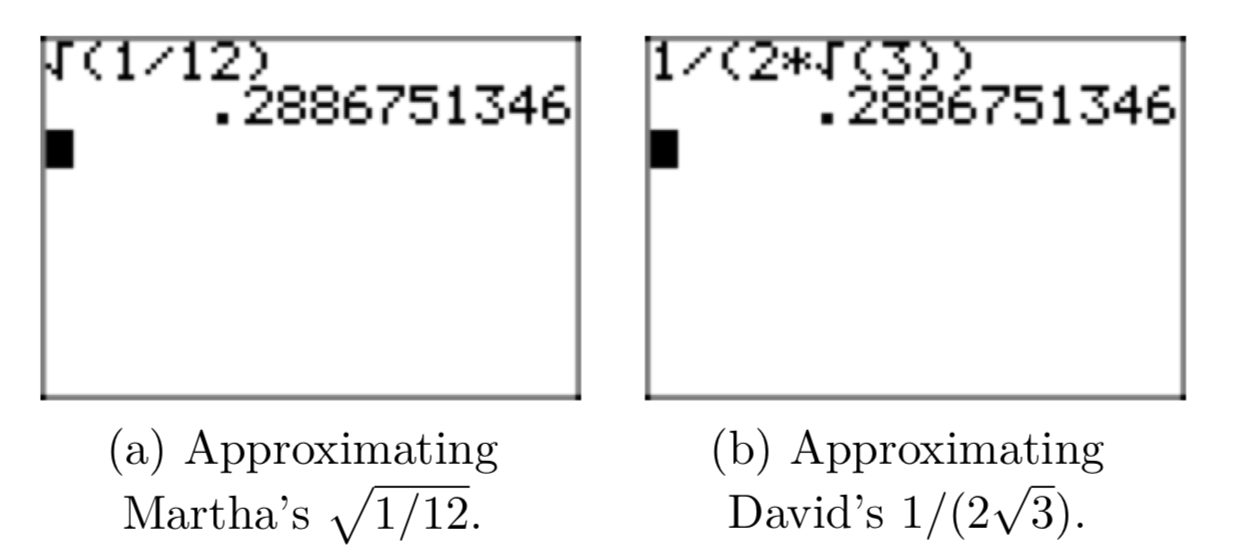
Martha lo encuentra\(\sqrt{\frac{1}{12}} \approx 0.2886751346\) y David lo encuentra\(\frac{1}{(2\sqrt{3})} \approx 0.2886751346\). Concluyen que sus respuestas coinciden, pero quieren saber por qué respuestas de aspecto tan diferente son idénticas.
El siguiente cálculo muestra por qué el resultado de Martha es idéntico al de David. primero, use la propiedad de división de los radicales (Propiedad 1) para tomar la raíz cuadrada tanto del numerador como del denominador.
\[\sqrt{\frac{1}{12}} = \frac{\sqrt{1}}{\sqrt{12}} = \frac{1}{\sqrt{12}}\]
A continuación, utilice la “primera pauta para la forma radical simple” y factorizar un cuadrado perfecto desde el denominador.
\[\frac{1}{\sqrt{12}} = \frac{1}{\sqrt{4}\sqrt{3}} = \frac{1}{2\sqrt{3}}\]
Esto demuestra claramente que las soluciones de David y Martha son idénticas.
En efecto, existen otras formas posibles para la solución del ejercicio hogar-laboral de David y Martha. Comience con la solución de Martha, luego multiplique tanto el numerador como el de- nominador de la fracción bajo el radical por 3.
\[\sqrt{\frac{1}{12}} = \sqrt{\frac{1}{12} \cdot \frac{3}{3}} = \sqrt{\frac{3}{36}}\]
Ahora, use la propiedad de división de los radicales (Propiedad 1), tomando la raíz cuadrada tanto del numerador como del denominador.
\[\sqrt{\frac{3}{36}} = \frac{\sqrt{3}}{\sqrt{36}} = \frac{\sqrt{3}}{6}\]
Obsérvese que la aproximación de aproximaciones de\(\frac{\sqrt{3}}{6}\) la Figura 3 es idéntica a las aproximaciones de Martha y David en las Figuras 2 (a) y (b).
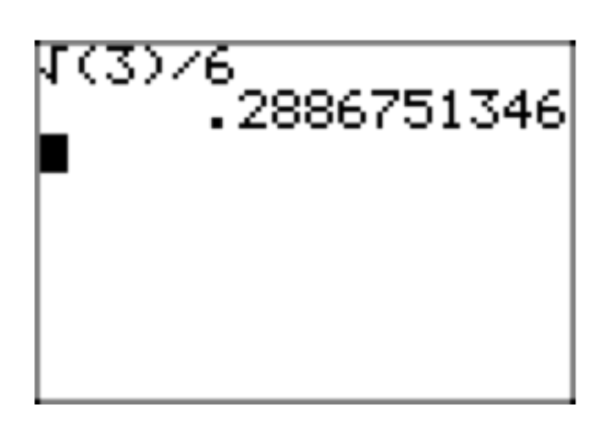
Si bien las tres formas de solución (\(\sqrt{\frac{1}{12}}\)\(\frac{1}{(2\sqrt{3})}\),, y\(\frac{\sqrt{3}}{6}\)) son idénticas, es muy frustrante tener tantas formas, particularmente cuando queremos comparar soluciones. Entonces, nos llevan a establecer dos lineamientos más para la forma radical simple.
La Segunda Guía para la Forma Radical Simple
No deje fracciones bajo un radical.
Así, Martha's no\(\sqrt{\frac{1}{12}}\) está en forma simple radical, porque contiene una fracción debajo del radical.
La Tercera Guía para la Forma Radical Simple
No dejes radicales en el denominador de una fracción.
Así, la de David no\(\frac{1}{(2\sqrt{3})}\) está en forma simple radical, porque el denominador de su fracción contiene un radical.
Sólo la forma equivalente\(\frac{\sqrt{3}}{6}\) obedece a las tres reglas de la forma radical simple.
- No es posible factorizar un cuadrado perfecto de ningún radical en la expresión\(\frac{\sqrt{3}}{6}\).
- No hay fracciones bajo un radical en la expresión\(\frac{\sqrt{3}}{6}\).
- El denominador en la expresión no\(\frac{\sqrt{3}}{6}\) contiene radicales.
En este texto y en este curso, seguiremos siempre las tres pautas para la forma radical simple.
Forma Radical Simple
Cuando tu respuesta es una expresión radical:
- Si es posible, factorizar un cuadrado perfecto.
- No dejes fracciones bajo un radical.
- No dejes radicales en el denominador de una fracción.
En los ejemplos que siguen (y en los ejercicios), es útil si conoces los cuadrados de los primeros 25 enteros positivos. Los hemos enumerado en el margen para usted en la Tabla 1 para futuras referencias.
Coloquemos algunas expresiones radicales en forma radical simple. Comenzaremos con algunas expresiones radicales que contienen fracciones bajo un radical.
Ejemplo\(\PageIndex{2}\)
Colocar la expresión\(\sqrt{\frac{1}{8}}\) en forma radical simple.
Solución
La expresión\(\sqrt{\frac{1}{8}}\) contiene una fracción bajo un radical. Podríamos tomar la raíz cuadrada tanto del numerador como del denominador, pero eso produciría\(\frac{\sqrt{1}}{\sqrt{8}}\), lo que pone un radical en el denominador.
La mejor estrategia es cambiar la forma de para\(\frac{1}{8}\) que tengamos un cuadrado perfecto en el denominador antes de tomar la raíz cuadrada del numerador y denominador. Observamos que si multiplicamos 8 por 2, el resultado es 16, un cuadrado perfecto. Esto es esperanzador, por lo que comenzamos la simplificación multiplicando tanto el numerador como el denominador de\(\frac{1}{8}\) por 2.
\(\sqrt{\frac{1}{8}} = \sqrt{\frac{1}{8} \cdot \frac{2}{2}} = \sqrt{\frac{2}{16}}\)
Ahora tomamos la raíz cuadrada tanto del numerador como del denominador. Debido a que el denominador es ahora un cuadrado perfecto, el resultado no tendrá un radical en el denominador.
\(\sqrt{\frac{2}{16}} = \frac{\sqrt{2}}{\sqrt{16}} = \frac{\sqrt{2}}{4}\)
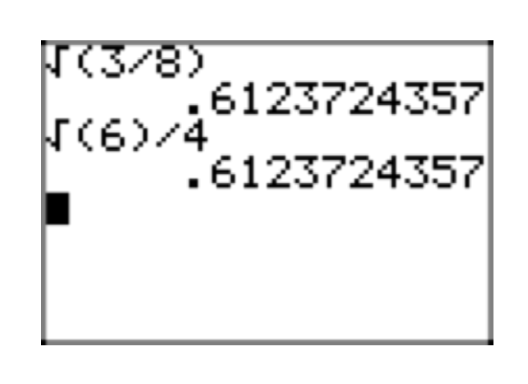
Este último resultado,\(\frac{\sqrt{2}}{4}\) está en forma radical simple. No es posible factorizar un cuadrado perfecto de ningún radical, no hay fracciones bajo ningún radical, y el denominador está libre de radicales.
Puede verificar fácilmente su solución usando su calculadora para comparar la expresión original con su forma radical simple. En la Figura 4 (a), hemos aproximado la expresión original,\(\sqrt{\frac{1}{8}}\). En la Figura 4 (b), hemos aproximado nuestra forma radical simple\(\frac{\sqrt{2}}{4}\). Tenga en cuenta que producen aproximaciones decimales idénticas.
Veamos otro ejemplo.
Ejemplo\(\PageIndex{3}\)
Colocar\(\sqrt{\frac{3}{20}}\) en forma radical simple.
Solución
Siguiendo el ejemplo del Ejemplo 2, observamos que\(5 \cdot 20 = 100\), un cuadrado perfecto. Entonces, multiplicamos tanto el numerador como el denominador por 5, luego tomamos la raíz cuadrada tanto del numerador como del denominador una vez que tenemos un cuadrado perfecto en el denominador.
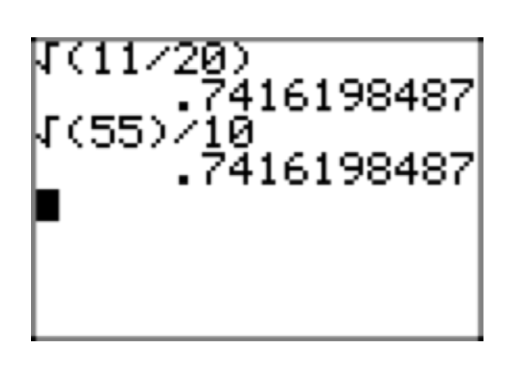
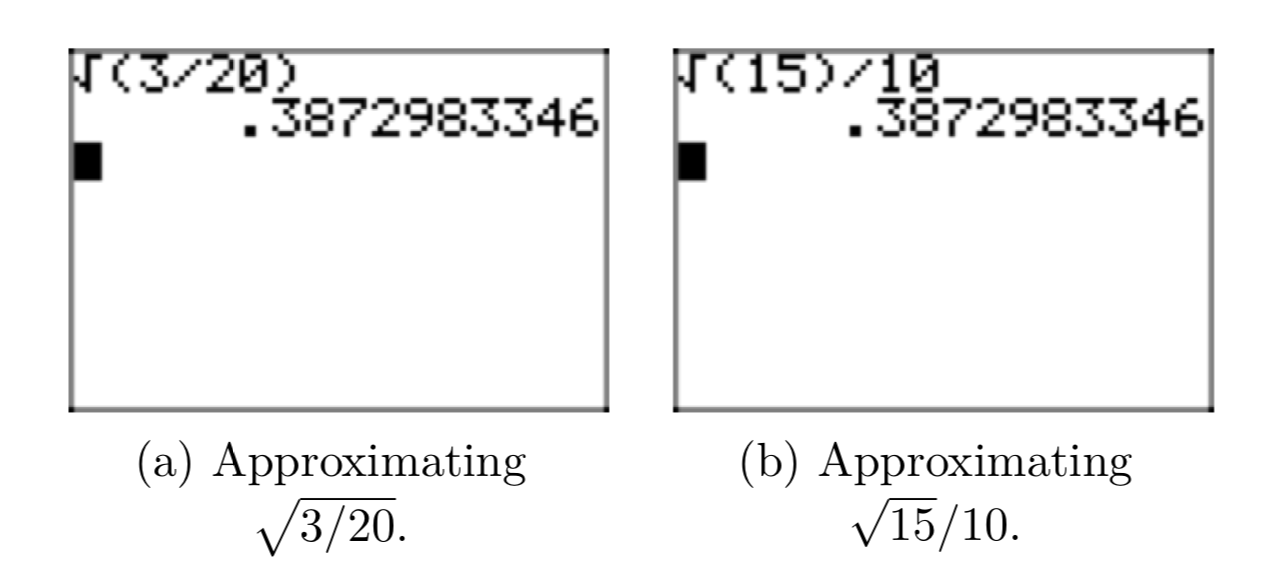
\(\sqrt{\frac{3}{20}} = \sqrt{\frac{3}{20} \cdot \frac{5}{5}} = \sqrt{\frac{15}{100}} = \frac{\sqrt{15}}{\sqrt{100}} = \frac{\sqrt{15}}{10}\)
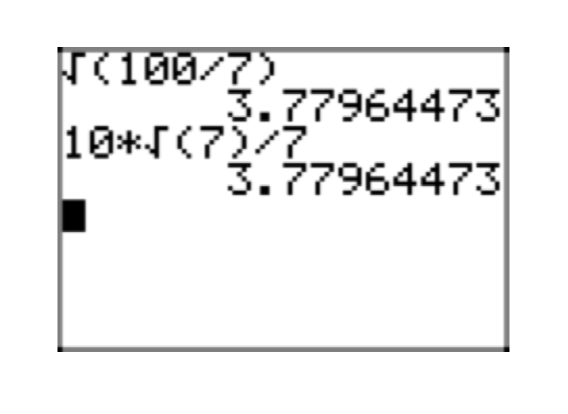
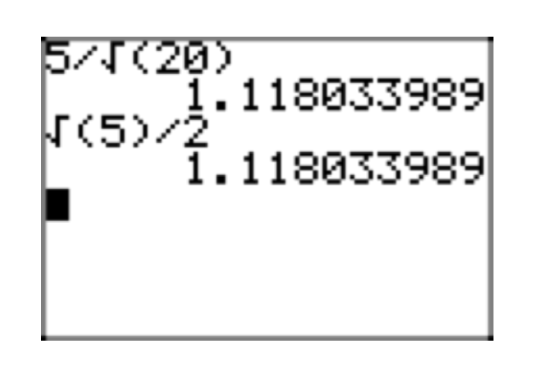
Obsérvese que la aproximación decimal de la forma radical simple\(\frac{\sqrt{15}}{10}\) en la Figura 5 (b) coincide con la aproximación decimal de la expresión original\(\frac{3}{20}\) en la Figura 5 (a).
Ahora vamos a mostrar cómo lidiar con una expresión que tiene un radical en su denominador, pero primero hacemos una pausa para explicar una nueva pieza de terminología.
Racionalización del Denominador
El proceso de eliminar radicales del denominador se llama racionalizar el denominador porque da como resultado una fracción donde el denominador está libre de radicales y es un número racional.
Ejercicio\(\PageIndex{4}\)
Colocar la expresión\(\frac{5}{\sqrt{18}}\) en forma radical simple.
Solución
En los ejemplos anteriores, hacer del denominador un cuadrado perfecto parecía una buena táctica. Aplicamos la misma táctica en este ejemplo, señalando que\(2 \cdot 18 = 36\) es un cuadrado perfecto. Sin embargo, la estrategia es ligeramente diferente, ya que comenzamos la solución multiplicando tanto el numerador como el denominador por\(\sqrt{2}\).
\[\frac{5}{\sqrt{18}} = \frac{5}{\sqrt{18}} \cdot \frac{\sqrt{2}}{\sqrt{2}}\]
Ahora multiplicamos numeradores y denominadores. En el denominador, se utiliza la propiedad de multiplicación de los radicales,\(\sqrt{18}\sqrt{2} = \sqrt{36}\).
\[\frac{5}{\sqrt{18}} \cdot \frac{\sqrt{2}}{\sqrt{2}} = \frac{5\sqrt{2}}{\sqrt{36}}\]
Ahora la estrategia debería ser clara. Porque el denominador es un cuadrado perfecto,\(\sqrt{36} = 6\), limpiando todos los radicales del denominador de nuestro resultado.
\[\frac{5\sqrt{2}}{\sqrt{36}} = \frac{5\sqrt{2}}{6}\]
El último resultado es en forma radical simple. No es posible extraer una raíz cuadrada perfecta de ningún radical, no hay fracciones bajo ningún radical, y el denominador está libre de radicales.
En la Figura 6, comparamos la aproximación de nuestra expresión original con\(\frac{5}{\sqrt{18}}\) nuestra forma radical simple\(\frac{5\sqrt{2}}{6}\).
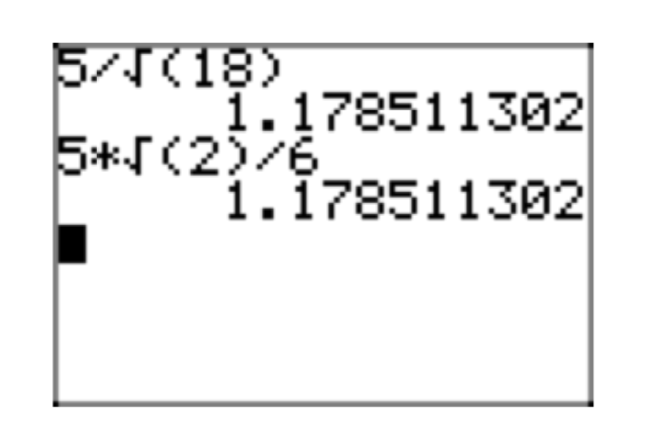
Veamos otro ejemplo.
Ejemplo\(\PageIndex{5}\)
Colocar la expresión\(\frac{18}{\sqrt{27}}\) en forma radical simple.
Solución
Tenga en cuenta que\(3 \cdot 27 = 81\) es un cuadrado perfecto. Comenzamos multiplicando tanto el numerador como el denominador de nuestra expresión\(\sqrt{3}\).
\(\frac{18}{\sqrt{27}} = \frac{18}{\sqrt{27}} \cdot \frac{\sqrt{3}}{\sqrt{3}}\)
Multiplicar numeradores y denominadores. En los denominadores,\(\sqrt{27}\sqrt{3} = \sqrt{81}\)
\(\frac{18}{\sqrt{27}} \cdot \frac{\sqrt{3}}{\sqrt{3}} = \frac{18\sqrt{3}}{\sqrt{81}}\)
Por supuesto,\(\sqrt{81} = 9\), entonces
\(\frac{18\sqrt{3}}{\sqrt{81}} = \frac{18\sqrt{3}}{9}\)
Ahora podemos reducir a términos más bajos, dividiendo el numerador y el denominador por 9.
\(\frac{18\sqrt{3}}{9} = 2\sqrt{3}\)
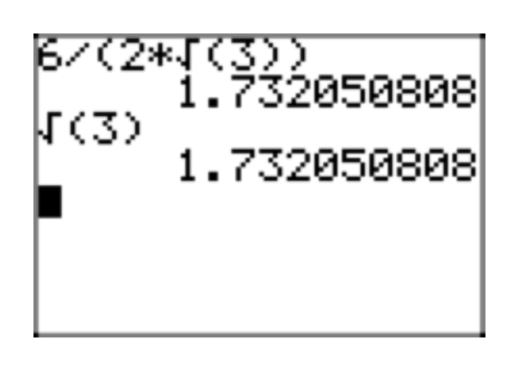
En la Figura 7, comparamos aproximaciones de la expresión original\(\frac{18}{\sqrt{27}}\) y su forma radical simple\(2\sqrt{3}\).
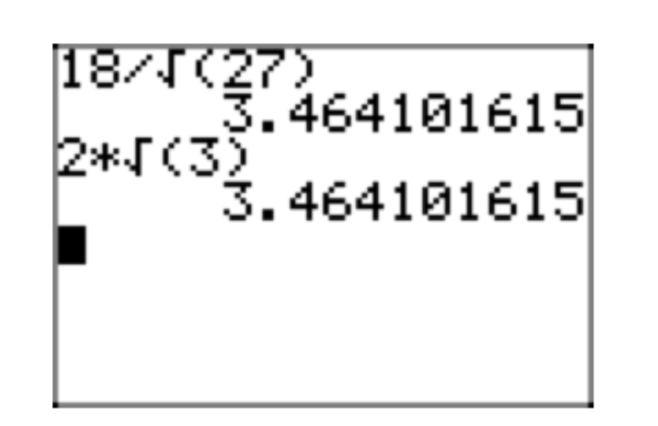
Consejos útiles
En la sección anterior, aprendimos que si cuadras un producto de expresiones exponenciales, multiplicas cada uno de los exponentes por 2.
\((2^{3}3^{4}5^{5})^2 = 2^{6}3^{8}5^{10}\)
Debido a que tomar la raíz cuadrada es lo “inverso” de la cuadratura, dividimos cada uno de los exponentes por 2.
\(\sqrt{2^{6}3^{8}5^{10}} = 2^{3}3^{4}5^{5}\)
También aprendimos que la factorización prima es una herramienta extremadamente poderosa que es bastante útil a la hora de colocar expresiones radicales en forma radical simple. Veremos que esto es aún más cierto en esta sección.
Veamos un ejemplo.
Ejemplo\(\PageIndex{6}\)
Colocar la expresión\(\sqrt{\frac{1}{98}}\) en forma radical simple.
Solución
A veces no es fácil averiguar cómo escalar el denominador para obtener un cuadrado perfecto, incluso cuando se le proporciona una mesa de cuadrados perfectos. Aquí es cuando el factor prime ization puede venir al rescate y proporcionar una pista. Entonces, primero expresamos el denominador como producto de primos en forma exponencial:\(98 = 2 \cdot 49 = 2 \cdot 7^2\)
\(\sqrt{\frac{1}{98}} = \sqrt{\frac{1}{2 \cdot 7^2}}\)
Ahora podemos ver fácilmente qué está impidiendo que el denominador sea un cuadrado perfecto. El problema es el hecho de que no todos los exponentes en el denominador son divisibles por 2. Podemos remediar esto multiplicando tanto el numerador como el denominador por 2.
\(\sqrt{\frac{1}{2 \cdot 7^2}} = \sqrt{\frac{1}{2 \cdot 7^2} \cdot \frac{2}{2}} = \sqrt{\frac{2}{2^{2}7^{2}}}\)
Tenga en cuenta que cada primo en el denominador ahora tiene un exponente que es divisible por 2. Ahora podemos tomar la raíz cuadrada tanto del numerador como del denominador.
\(\sqrt{\frac{2}{2^{2}7^{2}}} = \frac{\sqrt{2}}{\sqrt{2^{2}7^{2}}}\)
Toma la raíz cuadrada del denominador dividiendo cada exponente por 2.
\(\frac{\sqrt{2}}{\sqrt{2^{2}7^{2}}} = \frac{\sqrt{2}}{2^{1} \cdot 7^{1}}\)
Entonces, claro,\(2 \cdot 7 = 14\).
\(\frac{\sqrt{2}}{2 \cdot 7} = \frac{\sqrt{2}}{14}\)
En la Figura 8, observe cómo\(\frac{\sqrt{2}}{14}\) coinciden las aproximaciones decimales de la expresión original\(\sqrt{\frac{1}{98}}\) y su forma radical simple, fuerte evidencia de que hemos encontrado la forma radical simple correcta. Es decir, no podemos sacar un cuadrado perfecto de ningún radical, no hay fracciones bajo ningún radical, y los denominadores están claros de todos los radicales.
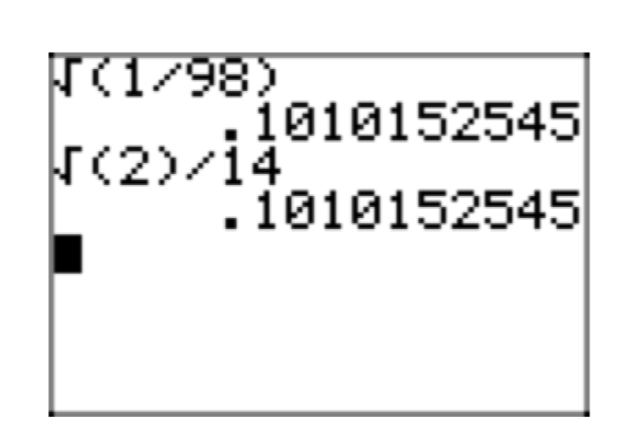
Veamos otro ejemplo.
Ejemplo\(\PageIndex{7}\)
Colocar la expresión\(\frac{12}{\sqrt{54}}\) en forma radical simple.
Solución
Factor primo el denominador:\( 54 = 2 \cdot 27 = 2 \cdot 3^3\).
\(\frac{12}{\sqrt{54}} = \frac{12}{\sqrt{2 \cdot 3^3}}\)
Ninguno de los primos en el denominador tiene un exponente divisible por 2. Si tuviéramos otro 2 y uno más 3, entonces los exponentes serían divisibles por 2. Esto nos anima a multiplicar tanto el numerador como el denominador por\(\sqrt{2 \cdot 3}\).
\(\frac{12}{\sqrt{2 \cdot 3^3}} = \frac{12}{\sqrt{2 \cdot 3^3}} \cdot \frac{\sqrt{2 \cdot 3}}{\sqrt{2 \cdot 3}} = \frac{12\sqrt{2 \cdot 3}}{\sqrt{2^{2}3^4}}\)
Divide cada uno de los exponentes en el denominador por 2.
\(\frac{12\sqrt{2 \cdot 3}}{\sqrt{2^{2}3^4}} = \frac{12\sqrt{2 \cdot 3}}{2^{1} \cdot 3^2}\)
Entonces, en el numerador,\(2 \cdot 3 = 6\), y en el denominador,\(2 \cdot 3^2 = 18\).
\(\frac{12\sqrt{2 \cdot 3}}{2 \cdot 3^{2}} = \frac{12\sqrt{6}}{18}\)
Por último, reducir a los términos más bajos dividiendo tanto el numerador como el denominador por 6.
\(\frac{12\sqrt{6}}{18} = \frac{2\sqrt{6}}{3}\)
En la Figura 9, la aproximación de la expresión original\(\frac{12}{\sqrt{54}}\) coincide con la de su forma radical simple\(\frac{2\sqrt{6}}{3}\)
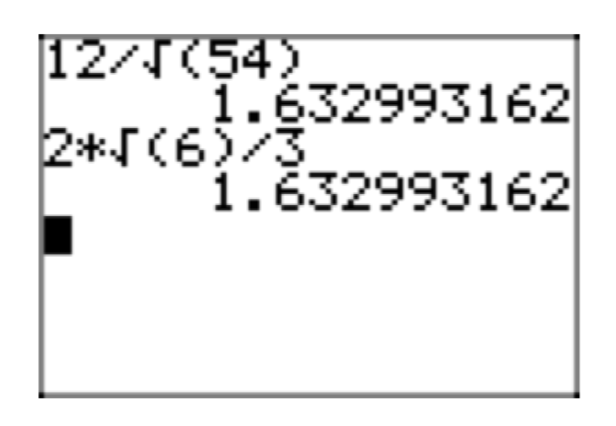
Expresiones variables
Si x es algún número real, recuerda de nuevo que
\[\sqrt{x^2} = |x| \nonumber \]
Si combinamos la ley de exponentes para cuadrar un cociente con nuestra propiedad por tomar la raíz cuadrada de un cociente, podemos escribir
\[\sqrt{(\frac{a}{b})^2} = \sqrt{\frac{a^2}{b^2}} = \frac{\sqrt{a^2}}{\sqrt{b^2}} \nonumber \]
Sin embargo,\(\sqrt{(\frac{a}{b})^2} = |\frac{a}{b}|\), mientras\(\frac{\sqrt{a^2}}{\sqrt{b^2}} = \frac{|a|}{|b|}\). Esta discusión lleva al siguiente resultado clave.
Regla de cociente para el valor absoluto
Si a y b son números reales, entonces
\[\left|\dfrac{a}{b}\right| = \frac{|a|}{|b|} \nonumber\]
siempre\(b \ne 0\). En palabras, el valor absoluto de un cociente es el cociente de los valores absolutos.
Vimos este inmueble anteriormente en el capítulo sobre la función de valor absoluto, donde brindamos un enfoque diferente a la prueba del inmueble. Es interesante que podamos probar esta propiedad de una manera completamente nueva usando las propiedades de raíz cuadrada. Veremos que tenemos necesidad de la Regla del Cociente para el Valor Absoluto en los ejemplos que siguen.
Por ejemplo, si x es cualquier número real excepto cero, usando la regla del cociente para el valor absoluto podríamos escribir
\[\left|\dfrac{3}{x}\right| = \frac{|3|}{|x|} = \frac{3}{|x|}\nonumber\]
Sin embargo, no hay manera de eliminar las barras de valor absoluto que rodean x a menos que sepamos el signo de x. Si x > 0 (recuerde, no hay ceros en el denominador), entonces |x| = x y la expresión se convierte en
\[\frac{3}{|x|} = \frac{3}{x} \nonumber \]
Por otro lado, si x < 0, entonces |x| = −x y la expresión se convierte
\[\frac{3}{|x|} = \frac{3}{−x} = −\frac{3}{x} \nonumber\]
Veamos otro ejemplo.
Ejemplo\(\PageIndex{8}\)
Colocar la expresión\(\sqrt{\frac{18}{x^6}}\) en forma radical simple. Discutir el dominio.
Solución
Tenga en cuenta que x no puede ser igual a cero, de lo contrario el denominador de\(\sqrt{\frac{18}{x^6}}\) sería cero, lo cual no está permitido. Sin embargo, si x es positivo o negativo,\(x^6\) will be a positive number (raising a nonzero number to an even power always produces a positive real number), and \(\sqrt{\frac{18}{x^6}}\) is well-defined.
Teniendo en cuenta que x es distinto de cero, pero podría ser positivo o negativo, procedemos invocando primero a la Propiedad 1, tomando la raíz cuadrada positiva tanto del numerador como del denominador de nuestra expresión radical.
\[\sqrt{\frac{18}{x^6}} = \frac{\sqrt{18}}{\sqrt{x^6}} \nonumber \]
Desde el numerador, factorizamos un cuadrado perfecto. En el denominador, utilizamos barras de valor absoluto para asegurar una raíz cuadrada positiva.
\(\frac{\sqrt{18}}{\sqrt{x^6}} = \frac{\sqrt{9}\sqrt{2}}{|x^3|} = \frac{3\sqrt{2}}{|x^3|}\)
Podemos usar la Regla de Producto para Valor Absoluto para escribir\(|x^3| = |x^2||x| = x^{2}|x|\). Tenga en cuenta que no necesitamos envolver\(x^2\) en barras de valor absoluto porque ya\(x^2\) es positivo.
\[\frac{3\sqrt{2}}{|x^3|} = \frac{3\sqrt{2}}{x^{2}|x|} \nonumber \]
Debido a que x podría ser positivo o negativo, no podemos eliminar las barras de valor absoluto alrededor de x.
Veamos otro ejemplo.
Ejemplo\(\PageIndex{9}\)
Colocar la expresión\(\sqrt{\frac{12}{x^5}}\) en forma radical simple. Discutir el dominio.
Solución
Tenga en cuenta que x no puede ser igual a cero, de lo contrario el denominador de\(\sqrt{\frac{12}{x^5}}\) sería cero, lo cual no está permitido. Además, si x es un número negativo, entonces también\(x^5\) será un número negativo (elevar un número negativo a una potencia impar produce un número negativo). Si x fuera negativo, entonces también\(\frac{12}{x^5}\) sería negativo y\(\sqrt{\frac{12}{x^5}}\) estaría indefinido (no se puede tomar la raíz cuadrada de un número negativo). Así, x debe ser un número real positivo o la expresión\(\sqrt{\frac{12}{x^5}}\) es indefinida.
Procedemos, teniendo en cuenta que\(x\) es un número real positivo. Un enfoque posible es señalar primero que se necesita otro factor de x para hacer del denominador un cuadrado perfecto. Esto nos motiva a multiplicar tanto el numerador como el denominador dentro del radical por\(x\).
\[\sqrt{\frac{12}{x^5}} = \sqrt{\frac{12}{x^5} \cdot \frac{x}{x}} = \sqrt{\frac{12x}{x^6}} \nonumber\]
Ahora podemos usar la Propiedad 1 para tomar la raíz cuadrada tanto del numerador como del denominador.
\[\sqrt{\frac{12x}{x^6}} = \frac{\sqrt{12x}}{\sqrt{x^6}} \nonumber\]
En el numerador, factorizamos un cuadrado perfecto. En el denominador, las barras de valor absoluto asegurarían una raíz cuadrada positiva. Sin embargo, hemos afirmado que x debe ser un número positivo, por lo que ya\(x^3\) es positivo y no se necesitan barras de valor absoluto.
\[\frac{\sqrt{12x}}{\sqrt{x^6}} = \frac{\sqrt{4}\sqrt{3x}}{x^3} = \frac{2\sqrt{3x}}{x^3} \nonumber\]
Veamos otro ejemplo.
Ejemplo\(\PageIndex{10}\)
Dado que x < 0, colocar\(\sqrt{\frac{27}{x^{10}}}\) en forma radical simple.
Solución
Un enfoque posible sería factorizar un cuadrado perfecto y escribir
\[\sqrt{\frac{27}{x^{10}}} = \sqrt{\frac{9}{x^{10}} \cdot \sqrt{3}} = \sqrt{(\frac{3}{x^5})^2}\sqrt{3} = |\frac{3}{x^5}|\sqrt{3}.\]
Ahora,\(|\frac{3}{x^5}| = \frac{|3|}{(|x^4||x|} = \frac{3}{x^{4}|x|}\), ya que\(x^4 > 0\). Por lo tanto,
\[|\frac{3}{x^5}|\sqrt{3} = \frac{3}{x^{4}|4|}\sqrt{3}. \nonumber \]
Sin embargo, se nos da que x < 0, entonces |x| = −x y podemos escribir
\[\frac{3}{x^{4}|x|}\sqrt{3} = \frac{3}{x^{4}|x|}\sqrt{3} = \frac{3}{x^{4}(−x)}\sqrt{3} = −\frac{3}{x^5}\sqrt{3}\]
Podemos movernos\(\sqrt{3}\) al numerador y escribir
\[−\frac{3}{x^5}\sqrt{3} = −\frac{3\sqrt{3}}{x^5}.\]
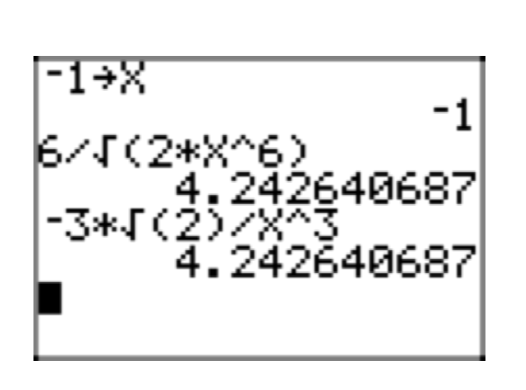
Nuevamente, es instructivo probar la validez de este resultado usando tu calculadora gráfica. Supuestamente, el resultado es verdadero para todos los valores de x < 0. Entonces, almacene −1 en x, luego ingrese la expresión original y su forma radical simple, luego compare las aproximaciones, como se muestra en las Figuras 10 (a), (b) y (c).
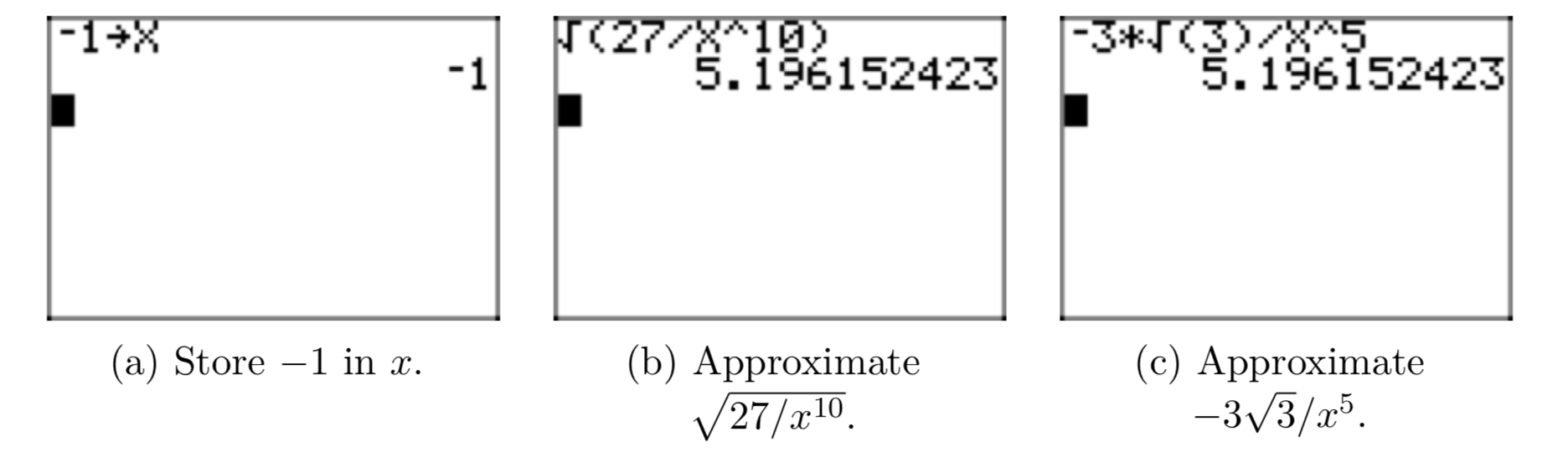
Enfoque alternativo. Un enfoque ligeramente diferente comenzaría de nuevo tomando la raíz cuadrada tanto del numerador como del denominador.
\(\sqrt{\frac{27}{x^{10}}} = \frac{\sqrt{27}}{\sqrt{x^{10}}}\)
Ahora,\(\sqrt{27} = \sqrt{9}\sqrt{3} = 3\sqrt{3}\) y aseguramos que\(\sqrt{x^{10}}\) produce un número positivo mediante el uso de barras de valor absoluto. Es decir,\(\sqrt{x^{10}} = |x^5|\) y
\(\frac{\sqrt{27}}{\sqrt{x^{10}}} = \frac{3\sqrt{3}}{|x^5|}\)
Sin embargo, utilizando la regla del producto para el valor absoluto y el hecho de que\(x^4 > 0\),\(|x^5| =|x^4||x| = x^{4}|x|\) y
\(\frac{3\sqrt{3}}{|x^5|} = \frac{3\sqrt{3}}{x^{4}|x|}\)
Finalmente, se nos da que x < 0, así |x| = −x y podemos escribir
\(\frac{3\sqrt{3}}{x^{4}|x|} = \frac{3\sqrt{3}}{x^{4}(−x)} = −\frac{3\sqrt{3}}{x^5}\).
Ejercicio\(\PageIndex{11}\)
Use una calculadora para aproximar primero\(\frac{\sqrt{5}}{\sqrt{2}}\). En la misma pantalla, aproximado\(\sqrt{\frac{5}{2}}\). Reporta los resultados en tu trabajo de tarea.
- Responder
-
Ambos\(\frac{\sqrt{5}}{\sqrt{2}} = \sqrt{\frac{5}{2}} \approx = 1.58113883\)
Ejercicio\(\PageIndex{2}\)
Use una calculadora para aproximar primero\(\frac{\sqrt{7}}{\sqrt{5}}\). En la misma pantalla, aproximado\(\sqrt{\frac{7}{5}}\). Reporta los resultados en tu trabajo de tarea.
Ejercicio\(\PageIndex{3}\)
Use una calculadora para aproximar primero\(\frac{\sqrt{12}}{\sqrt{2}}\). En la misma pantalla, aproximado\(\sqrt{6}\). Reporta los resultados en tu trabajo de tarea.
- Responder
-
Ambos\(\frac{\sqrt{12}}{\sqrt{2}} = \sqrt{6} \approx 2.449489743\).
Ejercicio\(\PageIndex{4}\)
Use una calculadora para aproximar primero\(\frac{\sqrt{15}}{\sqrt{5}}\). En la misma pantalla, aproximado\(\sqrt{3}\). Reporta los resultados en tu trabajo de tarea.
En los Ejercicios 5 - 16, coloque cada expresión radical en forma radical simple. Al igual que en el Ejemplo 2 en la narrativa, verifica tu resultado con tu calculadora.
Ejercicio\(\PageIndex{5}\)
\(\sqrt{\frac{3}{8}}\)
- Responder
-
\(\sqrt{\frac{3}{8}} = \sqrt{\frac{3}{8} \cdot \frac{2}{2}} = \sqrt{\frac{6}{16}} = \frac{\sqrt{6}}{4}\)
Ejercicio\(\PageIndex{6}\)
\(\sqrt{\frac{5}{12}}\)
Ejercicio\(\PageIndex{7}\)
\(\sqrt{\frac{11}{20}}\)
- Responder
-
\(\sqrt{\frac{11}{20}} = \sqrt{\frac{11}{20} \cdot \frac{5}{5}} = \sqrt{\frac{55}{100}} = \frac{\sqrt{55}}{10}\)
Ejercicio\(\PageIndex{8}\)
\(\sqrt{\frac{3}{2}}\)
Ejercicio\(\PageIndex{9}\)
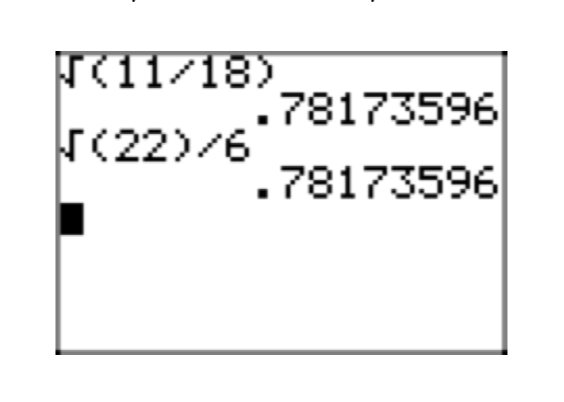
\(\sqrt{\frac{11}{18}}\)
- Responder
-
\(\sqrt{\frac{11}{18}} = \sqrt{\frac{11}{18} \cdot \frac{2}{2}} = \sqrt{\frac{22}{36}} = \frac{\sqrt{22}}{6}\)
Ejercicio\(\PageIndex{10}\)
\(\sqrt{\frac{7}{5}}\)
Ejercicio\(\PageIndex{11}\)
\(\sqrt{\frac{4}{3}}\)
- Responder
-
\(\sqrt{\frac{4}{3}} = \sqrt{\frac{4}{3} \cdot \frac{3}{3}} = \sqrt{\frac{12}{9}} = \frac{\sqrt{3}\sqrt{4}}{3}\)
Ejercicio\(\PageIndex{12}\)
\(\sqrt{\frac{16}{5}}\)
Ejercicio\(\PageIndex{13}\)
\(\sqrt{\frac{49}{12}}\)
- Responder
-
\(\sqrt{\frac{49}{12}} = \sqrt{\frac{49}{12} \cdot \frac{3}{3}} = \sqrt{\frac{49 \cdot 3}{36}} = \frac{\sqrt{49}\sqrt{3}}{6} = \frac{7\sqrt{3}}{6}\)
Ejercicio\(\PageIndex{14}\)
\(\sqrt{\frac{81}{20}}\)
Ejercicio\(\PageIndex{15}\)
\(\sqrt{\frac{100}{7}}\)
- Responder
-
\(\sqrt{\frac{100}{7}} = \sqrt{\frac{100}{7} \cdot \frac{7}{7}} = \sqrt{\frac{100 \cdot 7}{49}} = \frac{\sqrt{100}\sqrt{7}}{7} = \frac{10\sqrt{7}}{7}\)
Ejercicio\(\PageIndex{16}\)
\(\sqrt{\frac{36}{5}}\)
En los Ejercicios 17 - 28, colocar cada expresión radical en forma radical simple. Al igual que en el Ejemplo 4 en la narrativa, verifica tu resultado con tu calculadora.
Ejercicio\(\PageIndex{17}\)
\(\frac{1}{\sqrt{12}}\)
- Responder
-
\(\frac{1}{\sqrt{12}} = \frac{1}{\sqrt{12}} \cdot \frac{\sqrt{3}}{\sqrt{3}} = \frac{\sqrt{3}}{\sqrt{36}} = \frac{\sqrt{3}}{6}\)
Ejercicio\(\PageIndex{18}\)
\(\frac{1}{\sqrt{8}}\)
Ejercicio\(\PageIndex{19}\)
\(\frac{1}{\sqrt{20}}\)
- Responder
-
\(\frac{1}{\sqrt{20}} = \frac{1}{\sqrt{20}} \cdot \frac{\sqrt{5}}{\sqrt{5}} = \frac{\sqrt{5}}{\sqrt{100}} = \frac{\sqrt{5}}{10}\)
Ejercicio\(\PageIndex{20}\)
\(\frac{1}{\sqrt{27}}\)
Ejercicio\(\PageIndex{21}\)
\(\frac{6}{\sqrt{8}}\)
- Responder
-
\(\frac{6}{\sqrt{8}} = \frac{6}{\sqrt{8}} \cdot \frac{\sqrt{2}}{\sqrt{2}} = \frac{6\sqrt{2}}{\sqrt{16}} = \frac{6\sqrt{2}}{4} = \frac{3\sqrt{2}}{2}\)
Ejercicio\(\PageIndex{22}\)
\(\frac{4}{\sqrt{12}}\)
Ejercicio\(\PageIndex{23}\)
\(\frac{5}{\sqrt{20}}\)
- Responder
-
\(\frac{5}{\sqrt{20}} = \frac{5}{\sqrt{20}} \cdot \frac{\sqrt{5}}{\sqrt{5}} = \frac{5\sqrt{5}}{\sqrt{100}} = \frac{5\sqrt{5}}{10} = \frac{\sqrt{5}}{2}\)
Ejercicio\(\PageIndex{24}\)
\(\frac{9}{\sqrt{27}}\)
Ejercicio\(\PageIndex{25}\)
\(\frac{6}{2\sqrt{3}}\)
- Responder
-
\(\frac{6}{2\sqrt{3}} = \frac{6}{2\sqrt{3}} \cdot \frac{\sqrt{3}}{\sqrt{3}} = \frac{6\sqrt{3}}{2\sqrt{9}} =\frac{6\sqrt{3}}{6} = \sqrt{3}\)
Ejercicio\(\PageIndex{26}\)
\(\frac{10}{3\sqrt{5}}\)
Ejercicio\(\PageIndex{27}\)
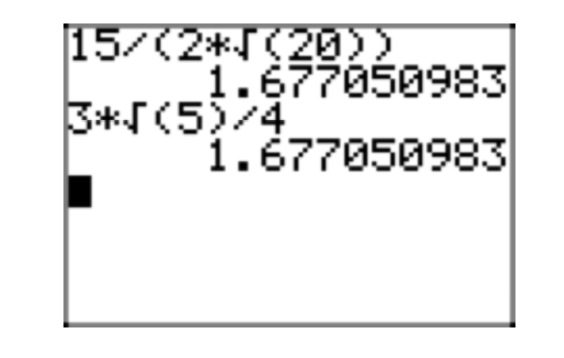
\(\frac{15}{2\sqrt{20}}\)
- Responder
-
\(\frac{15}{2\sqrt{20}} = \frac{15}{2\sqrt{20}} \cdot \frac{\sqrt{5}}{\sqrt{5}} = \frac{15\sqrt{5}}{2\sqrt{100}} = \frac{15\sqrt{5}}{20} = \frac{3\sqrt{5}}{4}\)
Ejercicio\(\PageIndex{28}\)
\(\frac{3}{2\sqrt{18}}\)
En los Ejercicios 29 - 36, colocar la expresión radical dada en forma simple. Usa la factorización prima como en el Ejemplo 8 en la narrativa para ayudarte con los cálculos. Al igual que en el Ejemplo 6, verifica tu resultado con tu calculadora.
Ejercicio\(\PageIndex{29}\)
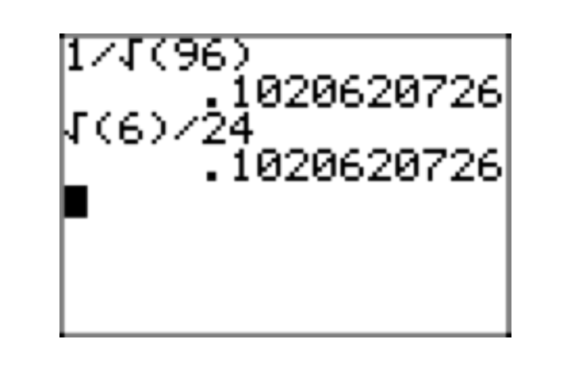
\(\frac{1}{\sqrt{96}}\)
- Responder
-
\(\frac{1}{\sqrt{96}} = \frac{1}{\sqrt{2^5 \cdot 3}} = \frac{1}{\sqrt{2^5 \cdot 3}} \cdot \frac{\sqrt{2 \cdot 3}}{\sqrt{2 \cdot 3}} = \frac{\sqrt{2 \cdot 3}}{2^6 \cdot 3^2} = \frac{\sqrt{2 \cdot 3}}{2^3 \cdot 3} = \frac{\sqrt{6}}{24}\)
Ejercicio\(\PageIndex{30}\)
\(\frac{1}{\sqrt{432}}\)
Ejercicio\(\PageIndex{31}\)
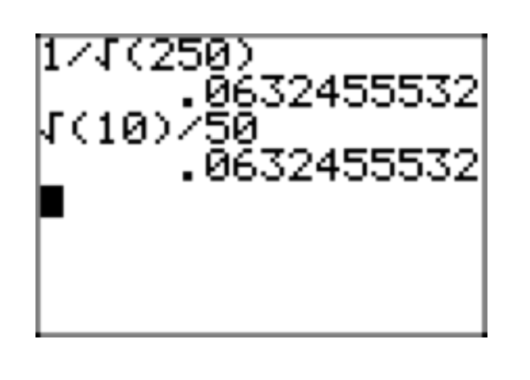
\(\frac{1}{\sqrt{250}}\)
- Responder
-
\(\frac{1}{\sqrt{250}} = \frac{1}{\sqrt{2 \cdot 5^3}} = \frac{1}{\sqrt{2 \cdot 5^3}} \cdot \frac{\sqrt{2 \cdot 5}}{\sqrt{2 \cdot 5}} = \frac{\sqrt{2 \cdot 5}}{2^2 \cdot 5^4} = \frac{\sqrt{2 \cdot 5}}{2 \cdot 5^2} = \frac{\sqrt{10}}{50}\)
Ejercicio\(\PageIndex{32}\)
\(\frac{1}{\sqrt{108}}\)
Ejercicio\(\PageIndex{33}\)
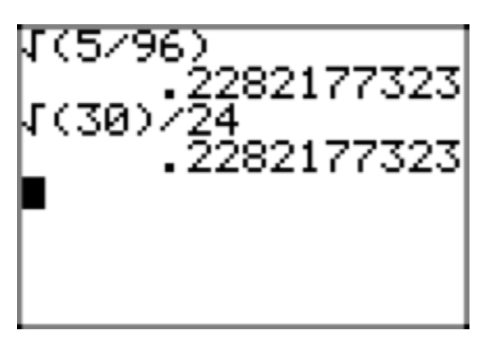
\(\sqrt{\frac{5}{96}}\)
- Responder
-
\(\sqrt{\frac{5}{96}} = \sqrt{\frac{5}{2^5 \cdot 3}} = \sqrt{\frac{5}{2^5 \cdot 3} \cdot \frac{2 \cdot 3}{2 \cdot 3}} = \sqrt{\frac{2 \cdot 3 \cdot 5}{2^6 \cdot 3^2}} = \frac{\sqrt{2 \cdot 3 \cdot 5}}{2^3 \cdot 3} = \frac{\sqrt{30}}{24}\)
Ejercicio\(\PageIndex{34}\)
\(\sqrt{\frac{2}{135}}\)
Ejercicio\(\PageIndex{35}\)
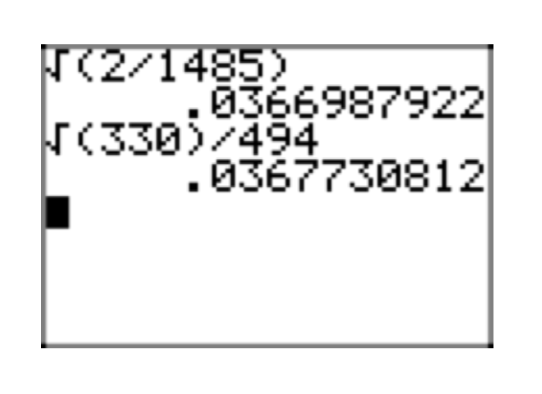
\(\sqrt{\frac{2}{1485}}\)
- Responder
-
\(\sqrt{\frac{2}{1485}} = \sqrt{\frac{2}{3^3 \cdot 5 \cdot 11}} = \sqrt{\frac{2}{3^3 \cdot 5 \cdot 11} \cdot \frac{3 \cdot 5 \cdot 11}{3 \cdot 5 \cdot 11}} = \sqrt{\frac{2 \cdot 3 \cdot 5 \cdot 11}{3^4 \cdot 5^2 \cdot 11^2}} = \frac{\sqrt{2 \cdot 3 \cdot 5 \cdot 11}}{3^2 \cdot 5 \cdot 11} = \frac{\sqrt{330}}{494}\)
Ejercicio\(\PageIndex{36}\)
\(\sqrt{\frac{3}{280}}\)
En los Ejercicios 37 - 44, coloque cada una de las expresiones radicales dadas en forma radical simple. No hacer suposiciones sobre el signo de ninguna variable. Las variables pueden representar números positivos o negativos.
Ejercicio\(\PageIndex{37}\)
\(\sqrt{\frac{8}{x^4}}\)
- Responder
-
\(\sqrt{\frac{8}{x^4}} = \frac{\sqrt{8}}{\sqrt{x^4}} = \frac{\sqrt{4}\sqrt{2}}{|x^2|} = \frac{2\sqrt{2}}{x^2}\)
Ejercicio\(\PageIndex{38}\)
\(\sqrt{\frac{12}{x^6}}\)
Ejercicio\(\PageIndex{39}\)
\(\sqrt{\frac{20}{x^2}}\)
- Responder
-
\(\sqrt{\frac{20}{x^2}} = \frac{\sqrt{20}}{\sqrt{x^2}} = \frac{\sqrt{4}\sqrt{5}}{|x|} = \frac{2\sqrt{5}}{|x|}\)
Ejercicio\(\PageIndex{40}\)
\(\sqrt{\frac{32}{x^{12}}}\)
Ejercicio\(\PageIndex{41}\)
\(\frac{2}{\sqrt{8x^8}}\)
- Responder
-
\(\frac{2}{\sqrt{8x^8}} = \frac{2}{\sqrt{8x^8}} \cdot \frac{\sqrt{2}}{\sqrt{2}} = \frac{2\sqrt{2}}{\sqrt{16x^8}} = \frac{2\sqrt{2}}{|4x^4|} = \frac{2\sqrt{2}}{4x^4}\)
Ejercicio\(\PageIndex{42}\)
\(\frac{3}{\sqrt{12x^6}}\)
Ejercicio\(\PageIndex{43}\)
\(\frac{10}{\sqrt{20x^{10}}}\)
- Responder
-
\(\frac{10}{\sqrt{20x^{10}}} = \frac{10}{\sqrt{20x^{10}}} \cdot \frac{\sqrt{5}}{\sqrt{5}} = \frac{10\sqrt{5}}{\sqrt{100x^{10}}} = \frac{10\sqrt{5}}{|10x^5|}\)
Sin embargo,\(|10x^5| = |10||x^4||x| = 10x^{4}|x|\), entonces
\(\frac{10}{\sqrt{20x^{10}}} = \frac{10\sqrt{5}}{10x^{4}|x|} = \frac{\sqrt{5}}{x^{4}|x|}\).
Ejercicio\(\PageIndex{44}\)
\(\frac{12}{\sqrt{6x^4}}\)
En los Ejercicios 45-48, siga el ejemplo del Ejemplo 8 en la narrativa para elaborar una solución.
Ejercicio\(\PageIndex{45}\)
Dado que x < 0, coloque la expresión radical\(\frac{6}{\sqrt{2x^6}}\) en forma radical simple. Verifique su solución en su calculadora para x = −1.
- Responder
-
\(\frac{6}{\sqrt{2x^6}} = \frac{6}{\sqrt{2x^6}} \cdot \frac{\sqrt{2}}{\sqrt{2}} = \frac{6\sqrt{2}}{\sqrt{4x^6}} = \frac{6\sqrt{2}}{|2x^3|}\)
Sin embargo,\(|2x^3| = |2||x^2||x| = 2x^{2}|x|\), entonces
\(\frac{6\sqrt{2}}{|2x^3|} = \frac{6\sqrt{2}}{2x^{2}|x|} = \frac{3\sqrt{2}}{x^{2}|x|}\).
Si x < 0, entonces |x| = −x y
\(\frac{3\sqrt{2}}{x^{2}|x|} = \frac{3\sqrt{2}}{x^{2}(−x)} = −\frac{3\sqrt{2}}{x^3}\).
Comprobando x = −1.
Ejercicio\(\PageIndex{46}\)
Dado que x > 0, colocar la expresión radical\(\frac{4}{\sqrt{12x^3}}\) en forma radical simple. Consulta tu solución en tu calculadora para x = 1.
Ejercicio\(\PageIndex{47}\)
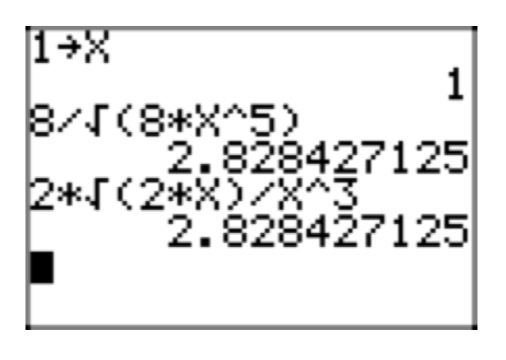
Dado que x > 0, colocar la expresión radical\(\frac{8}{\sqrt{8x^5}}\) en forma radical simple. Consulta tu solución en tu calculadora para x = 1.
- Responder
-
\(\frac{8}{\sqrt{8x^5}} = \frac{8}{\sqrt{8x^5}} \cdot \frac{\sqrt{2x}}{\sqrt{2x}} = \frac{8\sqrt{2x}}{\sqrt{16x^6}} = \frac{8\sqrt{2x}}{|4x^3|}\)
Sin embargo,\(|4x^3| = |4||x^2||x| = 4x^{2}|x|\), entonces
\(\frac{8\sqrt{2x}}{|4x^3|} = \frac{8\sqrt{2x}}{4x^{2}|x|} = \frac{2\sqrt{2x}}{x^{2}|x|}\).
Pero x > 0, entonces |x| = x y
\(\frac{2\sqrt{2x}}{x^{2}|x|} = \frac{2\sqrt{2x}}{x^{2}(x)} = \frac{2\sqrt{2x}}{x^3}\).
Comprobando x = 1.
Ejercicio\(\PageIndex{48}\)
Dado que x < 0, coloque la expresión radical\(\frac{15}{\sqrt{20x^6}}\) en forma radical simple. Verifique su solución en su calculadora para x = −1.
En los Ejercicios 49 - 56, coloque cada una de las expresiones radicales en forma simple. Supongamos que todas las variables representan números positivos.
Ejercicio\(\PageIndex{49}\)
\(\sqrt{\frac{12}{x}}\)
- Responder
-
\(\sqrt{\frac{12}{x}} = \sqrt{\frac{12}{x} \cdot \frac{x}{x}} = \sqrt{\frac{12x}{x^2}} = \frac{\sqrt{4}\sqrt{3x}}{\sqrt{x^2}} = \frac{2\sqrt{3x}}{x}\)
Ejercicio\(\PageIndex{50}\)
\(\sqrt{\frac{18}{x}}\)
Ejercicio\(\PageIndex{51}\)
\(\sqrt{\frac{50}{x^3}}\)
- Responder
-
\(\sqrt{\frac{50}{x^3}} = \sqrt{\frac{50}{x^3} \cdot \frac{x}{x}} = \sqrt{\frac{50x}{x^4}} = \frac{\sqrt{25}\sqrt{2x}}{\sqrt{x^4}} = \frac{5\sqrt{2x}}{x^2}\)
Ejercicio\(\PageIndex{52}\)
\(\sqrt{\frac{72}{x^5}}\)
Ejercicio\(\PageIndex{53}\)
\(\frac{1}{\sqrt{50x}}\)
- Responder
-
\(\frac{1}{\sqrt{50x}} = \frac{1}{\sqrt{50x}} \cdot \frac{\sqrt{2x}}{\sqrt{2x}} = \frac{\sqrt{2x}}{\sqrt{100x^2}} = \frac{\sqrt{2x}}{10x}\)
Ejercicio\(\PageIndex{54}\)
\(\frac{2}{\sqrt{18x}}\)
Ejercicio\(\PageIndex{55}\)
\(\frac{3}{\sqrt{27x^3}}\)
- Contestar
-
\(\frac{3}{\sqrt{27x^3}} = \frac{3}{\sqrt{27x^3}} \cdot \frac{\sqrt{3x}}{\sqrt{3x}} = \frac{3\sqrt{3x}}{\sqrt{81x^4}} = \frac{3\sqrt{3x}}{9x^2} = \frac{\sqrt{3x}}{3x^2}\)
Ejercicio\(\PageIndex{56}\)
\(\frac{5}{\sqrt{10x^5}}\)