9.2: Propiedades de multiplicación de radicales
- Page ID
- 110701
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
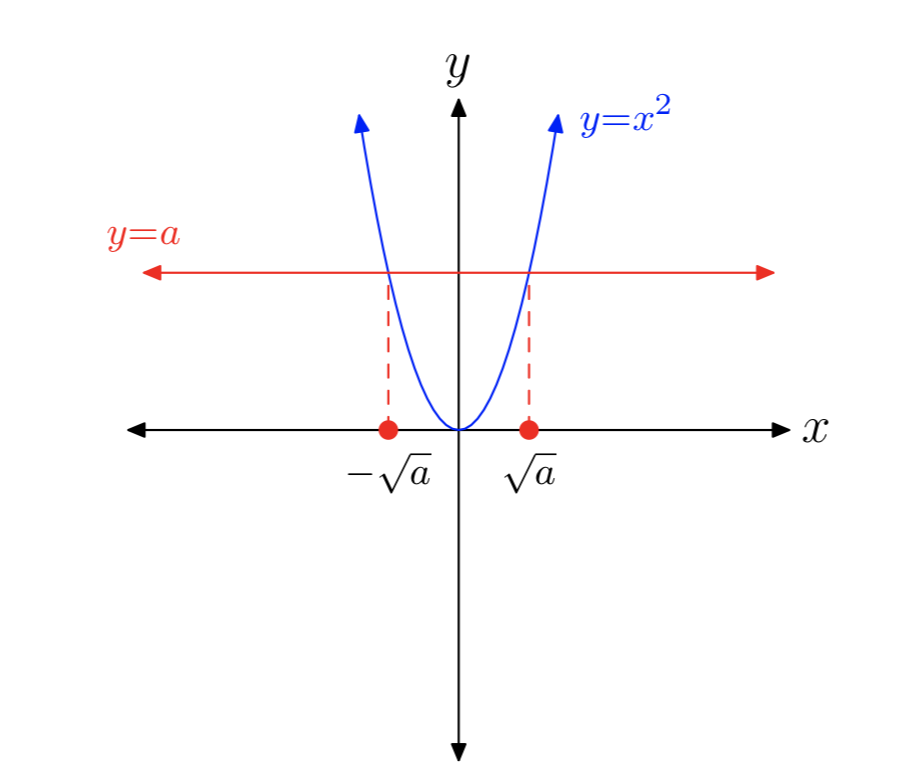
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Recordemos que la ecuación\(x^2 = a\), donde a es un número real positivo, tiene dos soluciones, como se indica en la Figura 1.
Aquí están los hechos clave.
Solución
Soluciones de\(x^2 = a\). Si a es un número real positivo, entonces:
- La ecuación\(x^2 = a\) tiene dos soluciones reales.
- La notación\(\sqrt{a}\) denota la solución real positiva única.
- La notación\(−\sqrt{a}\) denota la solución real negativa única.
Tenga en cuenta el uso de la palabra único. Cuando decimos que la solución\(\sqrt{a}\) es la única solución positiva real, queremos decir que es la única. No hay otros números reales positivos que sean soluciones de\(x^2 = a\). Una afirmación similar se mantiene para la solución negativa única.
Así, las ecuaciones\(x^2 = a\) y\(x^2 = b\) tienen soluciones positivas únicas\(x = \sqrt{a}\) y\(x = \sqrt{b}\), respectivamente, proporcionan que a y b son números reales positivos. Además, debido a que son soluciones, pueden ser sustituidas en las ecuaciones\(x^2 = a\) y\(x^2 = b\) para producir los resultados
\((\sqrt{a})^2 = a\)y\((\sqrt{b})^2 = b\)
respectivamente. Nuevamente, estos resultados dependen del hecho de que a y b son números reales positivos.
Del mismo modo, la ecuación
\(x^2 = ab\)
tiene una solución positiva única\(x = \sqrt{ab}\), siempre que a y b sean números positivos. Sin embargo, tenga en cuenta que
\((\sqrt{a}\sqrt{b})^2 = (\sqrt{a})^{2}(\sqrt{b})^{2} = ab\),
haciendo\(\sqrt{a}\sqrt{b}\) una segunda solución positiva de\(x^2 = ab\). Sin embargo, debido a que\(\sqrt{ab}\) es la única solución positiva de\(x^2 = ab\), esto obliga
\(\sqrt{ab} = \sqrt{a}\sqrt{b}\)
Esta discusión lleva a la siguiente propiedad de los radicales.
Propiedad 1
Dejar\(a\) y\(b\) ser números reales positivos. Entonces,
\[\sqrt{ab} = \sqrt{a}\sqrt{b}\]
Este resultado se puede utilizar de dos maneras claramente diferentes.
- Puedes usar el resultado para multiplicar dos raíces cuadradas, como en
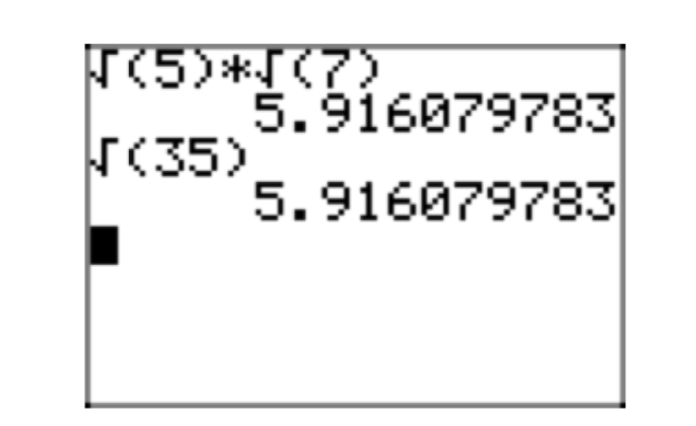
\(\sqrt{7}\sqrt{5} = \sqrt{35}\).
- \(\sqrt{35} = \sqrt{7}\sqrt{5}\)
Es interesante verificar este resultado en la calculadora, como se muestra en la Figura 2.
Forma Radical Simple
En esta sección introducimos el concepto de forma radical simple, pero primero comencemos con una pequeña historia. Martha y David están estudiando juntos, trabajando un problema de tarea a partir de su libro de texto. Martha llegó a una respuesta de\(\sqrt{32}\), mientras que David obtiene el resultado\(2\sqrt{8}\). Al principio, David y Martha creen que sus soluciones son números diferentes, pero antes se han equivocado por lo que deciden comparar aproximaciones decimales de sus resultados en sus calculadoras. El resultado de Martha se muestra en la Figura 3 (a), mientras que el de David se muestra en la Figura 3 (b).

Martha encuentra eso\(\sqrt{32} \approx 5.656854249\) y David encuentra esa su solución\(2\sqrt{8} \approx 5.656854249\). David y Martha concluyen que sus soluciones coinciden, pero quieren saber por qué las dos expresiones radicales de aspecto muy diferente son idénticas.
El siguiente cálculo, utilizando la Propiedad 1, muestra por qué el resultado de David es idéntico al de Martha.
\(\sqrt{32}=\sqrt{4}\sqrt{8}=2\sqrt{8}\)
En efecto, incluso hay una tercera posibilidad, una que es muy diferente a los resultados encontrados por David y Martha. Considera el siguiente cálculo, que vuelve a utilizar el Inmueble 1.
\(\sqrt{32}=\sqrt{16}\sqrt{2}=4\sqrt{2}\)
En la Figura 4, observe que la aproximación decimal de\(4\sqrt{2}\) aproximaciones para\(\sqrt{32}\) (Resultado de Martha en la Figura 3 (a)) y\(2\sqrt{8}\) (Resultado de David en la Figura 3 (b)).
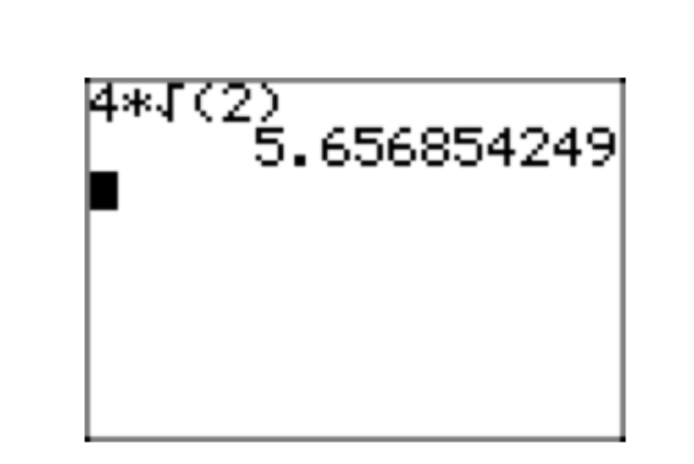
Si bien estas tres expresiones radicales (\(\sqrt{32}\)\(2\sqrt{8}\),, y\(4\sqrt{2}\)) son idénticas, es algo frustrante tener tantas formas diferentes, particularmente cuando queremos comparar soluciones. Por lo tanto, ofrecemos un conjunto de lineamientos para una forma especial de respuesta que llamaremos forma radical simple.
La Primera Guía para la Forma Radical Simple.
Cuando sea posible, factive un cuadrado perfecto.
Así, no\(\sqrt{32}\) está en forma radical simple, ya que es posible factorizar un cuadrado perfecto, como en
\(\sqrt{32}=\sqrt{16}\sqrt{2}=4\sqrt{2}\).
De igual manera, el resultado de David no\((2\sqrt{8})\) está en simple forma radical, porque él también puede factorizar un cuadrado perfecto de la siguiente manera.
\(2\sqrt{8}=2(\sqrt{4}\sqrt{2})=2(2\sqrt{2})=(2 \cdot 2)\sqrt{2}=4\sqrt{2}\).
Si tanto Martha como David siguen la “primera pauta para la forma radical simple”, su respuesta se verá idéntica (ambas iguales\(4\sqrt{2}\)). Esta es una de las principales ventajas de la forma radical simple: la capacidad de comparar soluciones.
En los ejemplos que siguen (y en los ejercicios), es útil si conoces los cuadrados de los primeros 25 enteros positivos. Los hemos enumerado en el margen para usted en la Tabla 1 para futuras referencias.
Coloquemos algunas expresiones más radicales en forma radical simple.

Ejemplo\(\PageIndex{3}\)
Colocar\(\sqrt{50}\) en forma radical simple.
- Contestar
-
En el Cuadro 1, 25 es un cuadrado. Porque\(50 = 25 \cdot 2\), podemos usar la Propiedad 1 para escribir
\(\sqrt{50}=\sqrt{25}\sqrt{2}=5\sqrt{2}\).
Ejemplo\(\PageIndex{4}\)
Colocar\(\sqrt{98}\) en forma radical simple.
- Contestar
-
En el Cuadro 1, 49 es un cuadrado. Porque\(98 = 49 \cdot 2\), podemos usar la Propiedad 1 para escribir
\(\sqrt{98}=\sqrt{49}\sqrt{2}=7\sqrt{2}\).
Ejemplo\(\PageIndex{5}\)
Colocar\(\sqrt{288}\) en forma radical simple.
- Contestar
-
Algunos estudiantes parecen capaces de arrancar de la nada el “cuadrado perfecto” óptimo. Si consulta la Tabla 1, notará que 144 es un cuadrado. Porque\(288 = 144 \cdot 2\), podemos escribir
\(\sqrt{288}=\sqrt{144}\sqrt{2}=12\sqrt{2}\).
Sin embargo, ¿y si te pierdes ese cuadrado perfecto superior\(288 = 4 \cdot 72\), piensas y escribes
\(\sqrt{288}=\sqrt{4}\sqrt{72}=2\sqrt{72}\).
Este enfoque no es incorrecto, siempre y cuando te des cuenta de que no has terminado. Aún puedes factorizar un cuadrado perfecto de 72. Porque\(72 = 36 \cdot 2\), puedes continuar y escribir
\(2\sqrt{72}=2(\sqrt{36}\sqrt{2})=2(6\sqrt{2})=(2\cdot 6)\sqrt{2}=12\sqrt{2}\).
Tenga en cuenta que llegamos a la misma forma radical simple, a saber\(12\sqrt{2}\). Simplemente nos llevó un poco más de tiempo. Mientras nos demos cuenta de que debemos continuar hasta que ya no podamos factorizar un cuadrado perfecto, llegaremos a la misma forma radical simple que el estudiante que parece sacar mágicamente el cuadrado superior de la nada.
En efecto, aquí hay otro enfoque que es igualmente válido.
\(\sqrt{288}=\sqrt{4}\sqrt{72}=2(\sqrt{4}\sqrt{18})=2(2\sqrt{18})=(2\cdot 2)\sqrt{18}=4\sqrt{18}\)
Tenemos que reconocer que todavía no estamos terminados porque podemos extraer otro cuadrado perfecto de la siguiente manera.
\(4\sqrt{18}=4(\sqrt{9}\sqrt{2})=4(3\sqrt{2})=(4\cdot 3)\sqrt{2}=12\sqrt{2}\)
Una vez más, mismo resultado. Sin embargo, tenga en cuenta que nos corresponde extraer el cuadrado más grande posible, ya que minimiza el número de pasos requeridos para alcanzar la forma radical simple.
Comprobación de Resultados con la Calculadora Gráfica. Una vez que hayas colocado una expresión radical en forma radical simple, puedes usar tu calculadora gráfica para verificar tu resultado. En este ejemplo, encontramos que
\(\sqrt{288}=12\sqrt{2}\). (6)
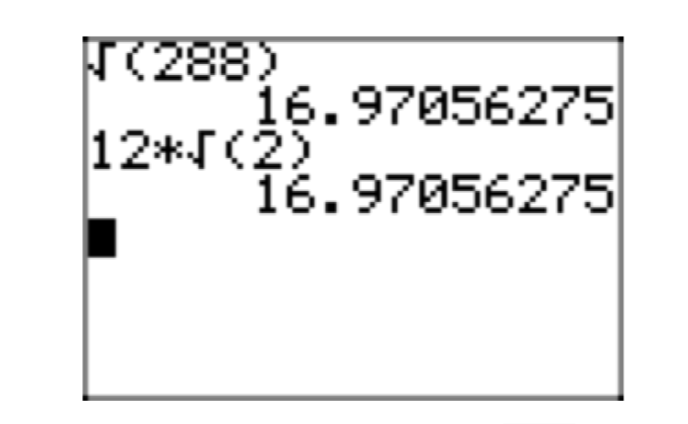
Ingrese los lados izquierdo y derecho de este resultado como se muestra en la Figura 5. Tenga en cuenta que cada
lado produce la misma aproximación decimal, verificando el resultado en la ecuación (6).
Consejos útiles
Recordemos que elevar una potencia de una base a otra potencia requiere que multipliquemos exponentes.
Elevar un Poder de una Base a otro Poder.
\((a^m)^n = a^{mn}\)
En particular, cuando cuadras una potencia de una base, debes multiplicar el exponente por 2. Por ejemplo,
\((2^5)^2 = 2^{10}\).
Por el contrario, debido a que tomar una raíz cuadrada es lo “inverso” de la cuadratura, al tomar una raíz cuadrada debemos dividir el exponente existente por 2, como en
\(\sqrt{2^{10}} = 2^5\).
Tenga en cuenta que la cuadratura\(2^5\) da\(2^{10}\), por lo que tomar la raíz cuadrada de\(2^{10}\) debe devolverle a\(2^5\). Cuando cuadras, duplicas el exponente. Por lo tanto, cuando tomas la raíz cuadrada, debes reducir a la mitad el exponente.
Del mismo modo,
- \((2^6)^2 = 2^{12}\)así\(\sqrt{2^{12}} = 2^6\).
- \((2^7)^2 = 2^{14}\)así\(\sqrt{2^{14}} = 2^7\).
- \((2^8)^2 = 2^{16}\)así\(\sqrt{2^{16}} = 2^8\).
Esto lleva al siguiente resultado.
Tomando la raíz cuadrada de un poder parejo.
Al tomar una raíz cuadrada de\(x^n\), cuando x es un número real positivo y n es un número natural par, divida el exponente entre dos. En símbolos,
\(\sqrt{x^n} = x^{\frac{n}{2}}\).
Obsérvese que esto concuerda con la definición de exponentes racionales presentada en el Capítulo 8, como en
\(\sqrt{x^n} = (x^n)^{\frac{1}{2}} = x^{\frac{n}{2}}\).
En otra nota, recordemos que elevar un producto a una potencia requiere que elevemos cada factor a esa potencia.
Elevar un Producto a una Potencia.
\((ab)^n = a^{n}b^{n}\).
En particular, si cuadras un producto, debes cuadrar cada factor. Por ejemplo,
\((5^{3}7^{4})^2 = (5^3)^{2}(7^4)^2 = 5^{6}7^{8}\).
Tenga en cuenta que multiplicamos cada exponente existente en este producto por 2.
La propiedad 1 es similar, en que cuando tomamos la raíz cuadrada de un producto, tomamos la raíz cuadrada de cada factor. Debido a que tomar una raíz cuadrada es la inversa de la cuadratura, debemos dividir cada exponente existente por 2, como en
\(\sqrt{5^{6}7^{8}} = \sqrt{5^{6}}\sqrt{7^{8}} = 5^{3}7^{4}\)
Veamos algunos ejemplos que emplean esta técnica.
Ejemplo\(\PageIndex{7}\)
Simplificar\(\sqrt{2^{4}3^{6}5^{10}}\)
- Contestar
-
Al tomar la raíz cuadrada de un producto de factores exponenciales, divida cada exponente por 2.
\(\sqrt{2^{4}3^{6}5^{10}} = 2^{2}3^{3}5^{5}\)
Si es necesario, puede expandir los factores exponenciales y multiplicarse para proporcionar una sola respuesta numérica.
\(2^{2}3^{3}5^{5} = 4 \cdot 27 \cdot 3125 = 337500\)
Se utilizó una calculadora para obtener la solución final.
Ejemplo\(\PageIndex{8}\)
Simplificar\(\sqrt{2^{5}3^{3}}\)
- Contestar
-
En este ejemplo, la dificultad es el hecho de que los exponentes no son divisibles por 2. Sin embargo, si es posible, la “primera pauta de forma radical simple” requiere que factoricemos un cuadrado perfecto. Entonces, extraiga cada factor elevado a la mayor potencia posible que sea divisible por 2, como en
\(\sqrt{2^{5}3^{3}} = \sqrt{2^{4}3^{2}}\sqrt{2 \cdot 3}\)
Ahora, divide cada exponente por 2.
\(\sqrt{2^{4}3^{2}}\sqrt{2\cdot 3} = 2^{2}3^{1}\sqrt{2 \cdot 3}\)
Finalmente, simplifique expandiendo cada factor exponencial y multiplicando.
\(2^{2}3^{1}\sqrt{2 \cdot 3} = 4 \cdot 3\sqrt{2 \cdot 3} = 12\sqrt{6}\)
Ejemplo\(\PageIndex{9}\)
Simplificar\(\sqrt{3^{7}5^{2}7^{5}}\).
- Contestar
-
Extraer cada factor a la mayor potencia posible que sea divisible por 2.
\(\sqrt{3^{7}5^{2}7^{5}} = \sqrt{3^{6}5^{2}7^{4}}\sqrt{3 \cdot 7}\)
Divide cada exponente por 2.
\(\sqrt{3^{6}5^{2}7^{4}}\sqrt{3 \cdot 7} = 3^{3}5^{1}7^{2}\sqrt{3 \cdot 7}\)
Expandir cada factor exponencial y multiplicar.
\(3^{3}5^{1}7^{2}\sqrt{3 \cdot 7} = 27 \cdot 5 \cdot 49 \sqrt{3 \cdot 7} =6615\sqrt{21}\)
Ejemplo\(\PageIndex{10}\)
Colocar\(\sqrt{216}\) en forma radical simple.
Si cebaremos al factor 216, podemos atacar este problema con la misma técnica utilizada en los ejemplos anteriores. Antes de que cebaremos el factor 216, aquí hay algunas pruebas de divisibilidad que podrían resultarle útiles.
Prueba de divisibilidad
- Si un número termina en 0, 2, 4, 6 u 8, es un número par y es divisible por 2.
- Si los dos últimos dígitos de un número forman un número que es divisible por 4, entonces el número entero es divisible por 4.
- Si un número termina en 0 o 5, es divisible por 5.
- Si la suma de los dígitos de un número es divisible por 3, entonces el número entero es divisible por 3.
- Si la suma de los dígitos de un número es divisible por 9, entonces el número entero es divisible por 9.
Por ejemplo, en orden:
- El número 226 termina en un 6, por lo que es parejo y divisible por 2. Efectivamente,\(226 = 2 \cdot 113\).
- Los dos últimos dígitos de 224 son 24, que es divisible por 4, por lo que el número completo es divisible por 4. Efectivamente,\(224 = 4 \cdot 56\).
- El último dígito de 225 es un 5. Por lo tanto 225 es divisible por 5. Efectivamente,\(225 = 5 \cdot 45\).
- La suma de los dígitos de 222 es 2 + 2 + 2 = 6, que es divisible por 3. Por lo tanto, 222 es divisible por 3. Efectivamente,\(222 = 3 \cdot 74\).
- La suma de los dígitos de 684 es 6 + 8 + 4 = 18, que es divisible por 9. Por lo tanto, 684 es divisible por 9. Efectivamente,\(684 = 9 \cdot 76\).
Ahora, vamos al factor 216. Tenga en cuenta que 2+1+6 = 9, así que 216 es divisible por 9. Efectivamente,\(216 = 9 \cdot 24\). En la Figura 6, utilizamos un “árbol factorial” para continuar factorizando hasta que todas las “hojas” sean números primos.
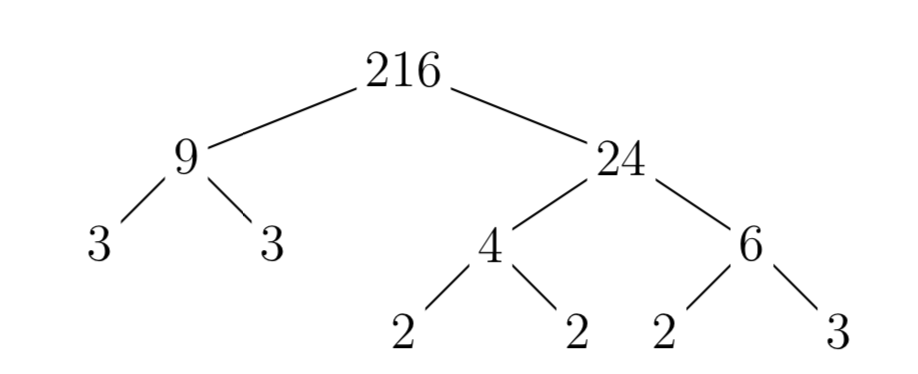
Por lo tanto,
\(216 = 2 \cdot 2 \cdot 2 \cdot 3 \cdot 3 \cdot 3\),
o en forma exponencial,
\(216 = 2^{3} \cdot 3^{3}\).
Por lo tanto,
\(\sqrt{216} = \sqrt{2^{3}3^{3}} = \sqrt{2^{2}3^{2}}\sqrt{2\cdot 3}=2 \cdot 3\sqrt{2 \cdot 3}=6\sqrt{6}\).
¡La factorización principal es una herramienta increíblemente útil!
Veamos otro ejemplo.
Ejemplo\(\PageIndex{11}\)
Colocar\(\sqrt{2592}\) en forma radical simple.
- Contestar
-
Si encontramos la factorización prima para 2592, podemos atacar este ejemplo usando la misma técnica que usamos en el ejemplo anterior. Observamos que la suma de los dígitos de 2592 es 2 + 5 + 9 + 2 = 18, que es divisible por 9. Por lo tanto, 2592 también es divisible por 9.
\(2592 = 9 \cdot 288\)
La suma de los dígitos de 288 es 2+8+8 = 18, que es divisible por 9, así que 288 también es divisible por 9.
\(2592 = 9 \cdot (9 \cdot 32)\)
Continúa de esta manera hasta que las hojas de tu “árbol factorial” sean todas primes. Entonces, deberías obtener
\(2592 = 2^{5}3^{4}\).
Por lo tanto,
\(\sqrt{2592} = \sqrt{2^{5}3^{4}} = \sqrt{2^{4}3^{4}}\sqrt{2} = 2^{2}3^{2}\sqrt{2} = 4 \cdot 9\sqrt{2}=36\sqrt{2}\).
Usemos la calculadora gráfica para verificar este resultado. Ingrese cada lado de\(\sqrt{2592} = 36\sqrt{2}\) por separado y compare aproximaciones, como se muestra en la Figura 7.
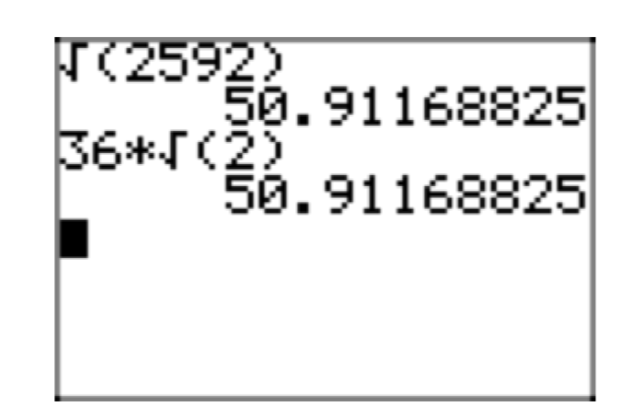
Figura 7. Comparando\(\sqrt{2592}\) con su forma radical simple\(36\sqrt{2}\).
Una propiedad importante de las raíces cuadradas
Uno de los errores más comunes en álgebra ocurre cuando se pide a los practicantes que simplifiquen la expresión\(\sqrt{x^2}\), donde x es cualquier número real arbitrario. Examinemos dos de los errores más comunes.
- Algunos afirmarán que la siguiente afirmación es cierta para cualquier número real arbitrario x.
\(\sqrt{x^2} = \pm x\).
Esto se ve fácilmente como incorrecto. Simplemente sustituya cualquier número real por x para verificar esta reclamación. Escogeremos x = 3 y lo sustituiremos en cada lado de la declaración propuesta.
\(\sqrt{3^2} = \pm 3\).
Si simplificamos el lado izquierdo, producimos el siguiente resultado.
\(\sqrt{3^2} = \pm 3\).
\(3 = \pm 3\)
No es correcto afirmar que 3 y\(\pm 3\) son iguales.
- Un segundo error es afirmar que
\(\sqrt{x^2} = x\)
para cualquier número real arbitrario x. Aunque esto es ciertamente cierto si sustituyes números no negativos por x, mira lo que sucede cuando sustituyes − 3 por x.
\(\sqrt{(−3)^2} = 3\)
Si simplificamos el lado izquierdo, producimos el siguiente resultado.
\(\sqrt{9} = −3\)
3 = −3
Claramente, 3 y − 3 no son iguales.
En ambos casos, lo que se ha olvidado es el hecho de que\(\sqrt{}\) exige una raíz cuadrada positiva (no negativa si se quiere incluir el caso\(\sqrt{0}\)). En ambos errores anteriores, es decir\(\sqrt{x^2} = \pm x\) y\(\sqrt{x^2} = x\), el lado izquierdo está pidiendo una respuesta no negativa, pero no se ha hecho nada para asegurar que el lado derecho también sea no negativo. ¿Algo me viene a la mente?
Claro, si envolvemos el lado derecho en valores absolutos, como en
\(\sqrt{x^2} = |x|\),
entonces ambas partes están pidiendo una respuesta no negativa. En efecto, tenga en cuenta que
\(\sqrt{(−3)^2} =|−3|\),\(\sqrt{0^2} =|0|\), y\(\sqrt{3^2} =|3|\)
son todas las declaraciones válidas.
Esta discusión lleva al siguiente resultado.
La raíz cuadrada positiva del cuadrado de x
Si x es cualquier número real, entonces
\(\sqrt{x^2} = |x|\),
La siguiente tarea es utilizar esta nueva propiedad para producir una propiedad extremadamente útil de valor absoluto.
Una propiedad de multiplicación de valor absoluto
Si combinamos la ley de exponentes para cuadrar un producto con nuestra propiedad para tomar la raíz cuadrada de un producto, podemos escribir
\(\sqrt{(ab)^2} = \sqrt{a^{2}b^{2}} = \sqrt{a^2}\sqrt{b^2}\).
Sin embargo,\(\sqrt{(ab)^2} = |ab|\), mientras\(\sqrt{a^2}{b^2} = |a||b|\). Esta discusión lleva al siguiente resultado.
Regla del producto para el valor absoluto
Si a y b son números reales,
|ab| = |a||b|.
En palabras, el valor absoluto de un producto es igual al producto de los valores absolutos.
Vimos este inmueble anteriormente en el capítulo sobre la función de valor absoluto, donde brindamos un enfoque diferente a la prueba del inmueble. Es interesante que podamos probar esta propiedad de una manera completamente nueva usando las propiedades de raíz cuadrada. Veremos que tenemos necesidad de la Regla de Producto para Valor Absoluto en los ejemplos que siguen.
Por ejemplo, usando la regla del producto, si x es cualquier número real, podríamos escribir
|3x| = |3||x| = 3|x|
Sin embargo, no hay manera de que podamos eliminar las barras de valor absoluto que rodean a x a menos que sepamos el signo de x. Si\(x \ge 0\), entonces |x| = x y la expresión se convierte
3|x| = 3x.
Por otro lado, si x < 0, entonces |x| = −x y la expresión se convierte
3|x| = 3 (−x) = −3x.
Veamos otro ejemplo. Usando la regla del producto, si x es cualquier número real, la expresión se\(| − 4x^3|\) puede manipular de la siguiente manera.
\(|−4x^3| = |−4||x^2||x|\)
Sin embargo, |−4|=4 y desde\(x^2 \ge 0\) para cualquier valor de x,\(|x^2|=x^2\). Por lo tanto,
\(|−4||x^2||x| = 4x^{2}|x|\).
Nuevamente, no hay manera de que podamos eliminar las barras de valor absoluto alrededor de x a menos que sepamos el signo de x. Si\(x \ge 0\), entonces|x|=x y
\(4x^{2}|x| = 4x^{2}(x) = 4x^3\).
Por otro lado, si x < 0, entonces |x| = −x y
\(4x^{2}|x| = 4x^{2}(−x) = −4x^3\).
Usemos estas ideas para simplificar algunas expresiones radicales que contienen variables.
Expresiones variables
Ejemplo\(\PageIndex{13}\)
Dado que la x representa cualquier número real, coloque la expresión radical
\(\sqrt{48x^6}\)
en forma radical simple.
La forma radical simple exige que factoricemos un cuadrado perfecto, si es posible. En este caso,\(48 = 16 \cdot 3\) y factorizamos la mayor potencia de x que es divisible por 2.
\(\sqrt{48x^6} = \sqrt{16x^6}\sqrt{3}\)
Ahora podemos usar la Propiedad 1 para tomar la raíz cuadrada de cada factor.
\(\sqrt{16x^6}\sqrt{3} = \sqrt{16}\sqrt{x^6}\sqrt{3}\)
Ahora bien, recuerde que la notación\(\sqrt{}\) requiere una raíz cuadrada no negativa, por lo que debemos asegurar que cada respuesta en la ecuación anterior no sea negativa. Por lo tanto,
\(\sqrt{16}\sqrt{x^6}\sqrt{3} = 4|x^3|\sqrt{3}\)
Algunos comentarios están en orden.
- La raíz cuadrada no negativa de 16 es 4. Es decir,\(\sqrt{16} = 4\)
- La raíz cuadrada no negativa de x6 es más difícil. Es incorrecto decirlo\(\sqrt{x^6} = x^3\), porque\(x^3\) podría ser negativo (si x es negativo). Para asegurar una raíz cuadrada no negativa, en este caso necesitamos envolver nuestra respuesta en barras de valor absoluto. Es decir,\(\sqrt{x^6} = |x^3|\).
Podemos usar la Regla de Producto para Valor Absoluto para escribir\(|x^3| = |x^2||x|\). Debido a que no\(x^2\) es negativo, las barras de valor absoluto son redundantes y no necesarias. Es decir,\(|x^2||x| = x^{2}|x|\). Así, podemos simplificar nuestra solución un poco más y escribir
\(4|x^3|\sqrt{3} = 4x^{2}|x|\sqrt{3}\)
Por lo tanto,
\(\sqrt{48x^6} = 4x^{2}|x|\sqrt{3}\).
Solución Alterna. Hay una variedad de formas en las que podemos colocar una expresión radical en forma radical simple. Aquí hay otro enfoque. Comenzando por el paso anterior, donde primero factorizamos un cuadrado perfecto,
\(\sqrt{48x^6} = \sqrt{16x^6}\sqrt{3}\)
nosotros podríamos escribir
\(\sqrt{16x^6}\sqrt{3} = \sqrt{(4x^3)^2}\sqrt{3}\).
Ahora bien, recordemos que la raíz cuadrada no negativa del cuadrado de una expresión es el valor absoluto de esa expresión (tenemos que garantizar una respuesta no negativa), entonces
\(\sqrt{(4x^3)^2}\sqrt{3} = |4x^3|\sqrt{3}\).
Sin embargo,\(|4x^3| = |4||x^3|\) por nuestra regla de producto y\(|4||x^3| = 4|x^3|\). Por lo tanto,
\(|4x^3|\sqrt{3} = 4|x^3|\sqrt{3}\).
Por último\(x^2 \ge 0\),\(|x^3| = |x^2||x| = x^2|x|\) porque, así podemos escribir
\(4|x^3|\sqrt{3} = 4x^{2}|x|\sqrt{3}\)
No podemos eliminar la barra de valor absoluto que rodea x a menos que sepamos el signo de x.
Nótese que la forma radical simple en la solución alternativa es idéntica a la forma radical simple encontrada con la técnica de solución anterior.
Veamos otro ejemplo.
Ejemplo\(\PageIndex{14}\)
Dado que x < 0, colocar\(\sqrt{24x^6}\) en forma radical simple.
Primero, factorizar un cuadrado perfecto y escribir
\(\sqrt{24x^6} = \sqrt{4x^6}\sqrt{6}\)
Ahora, use la Propiedad 1 y tome la raíz cuadrada de cada factor.
\(\sqrt{4x^6}\sqrt{6}= \sqrt{4}\sqrt{x^6}\sqrt{6}\)
Para asegurar una respuesta no negativa a\(\sqrt{x^6}\), envuelva su respuesta en valores absolutos.
\(\sqrt{4}\sqrt{x^6}\sqrt{6}=2|x^3|\sqrt{6}\)
No obstante, como en el problema anterior,\(|x^3| = |x^2||x| = x^{2}|x|\), ya que\(x^2 \ge 0\). Por lo tanto,
\(2|x^3|\sqrt{6} = 2x^{2}|x|\sqrt{6}\).
En este ejemplo, se nos dio el hecho extra de que x < 0, entonces |x| = −x y podemos escribir
\(2x^{2}|x|\sqrt{6} = 2x^{2}(−x)\sqrt{6} = −2x^{3}\sqrt{6}\).
Es instructivo probar la validez de la respuesta
\(\sqrt{24x^6} = −2x^{3}\sqrt{6}\), x<0.
usando una calculadora.

Es algo contrario a la intuición que el resultado
\(\sqrt{24x^6} = −2x^{3}\sqrt{6}\), x<0.
contiene un signo negativo. Después de todo, la expresión\(\sqrt{24x^6}\) llama a un resultado no negativo, pero tenemos un signo negativo. Sin embargo, en una inspección más cercana, si x < 0, entonces x es un número negativo y el lado derecho\(−2x^{3}\sqrt{6}\) es un número positivo (−2 es negativo,\(x^3\) es negativo porque x es negativo, y el producto de dos negativos es un positivo).
Veamos otro ejemplo.
Ejemplo\(\PageIndex{15}\)
Si x < 3, simplifique\(\sqrt{x^2−6x+9}\).
La expresión bajo el radical es un trinomio cuadrado perfecto y factores.
\(\sqrt{x^2−6x+9}=\sqrt{(x−3)^2}\)
Sin embargo, la raíz cuadrada no negativa del cuadrado de una expresión es el valor absoluto de esa expresión, por lo que
\(\sqrt{(x−3)^2} =|x−3|\).
Por último, porque se nos dice que x < 3, esto hace que x − 3 sea un número negativo, entonces
|x−3| = − (x−3).
Nuevamente, el resultado\(\sqrt{x^2−6x+9} = −(x−3)\), proporcionado x < 3, es algo contrario a la intuición ya que estamos esperando un resultado positivo. Sin embargo, si x < 3, el resultado − (x−3) es positivo. Puede probar esto sustituyendo varios valores de x que son menores que 3 en la expresión − (x−3) y señalando que el resultado es positivo. Por ejemplo, si x = 2, entonces x es menor que 3 y
− (x−3) = − (2−3) = − (−1) = 1,
lo que, por supuesto, es un resultado positivo.
Es aún más informativo señalar que nuestro resultado es equivalente a
\(\sqrt{x^2−6x+9}=−x+3\), x<3.
Esto se ve fácilmente distribuyendo el signo menos en el resultado − (x−3).
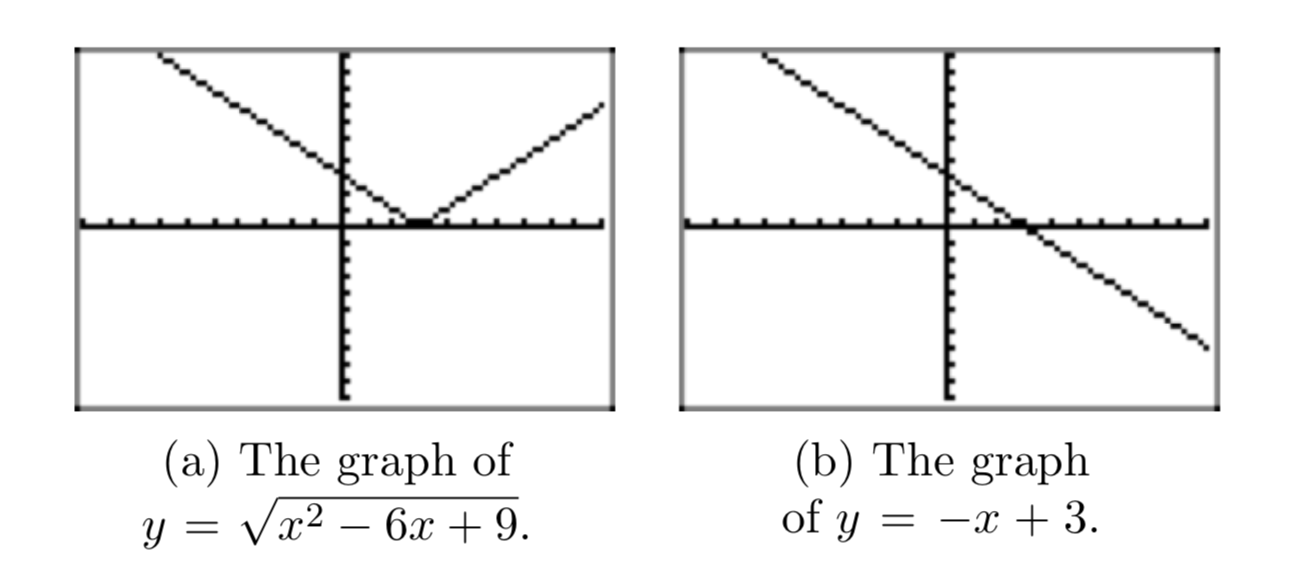
Hemos dibujado la gráfica de\(y = \sqrt{x^2−6x+9}\) en nuestra calculadora en la Figura 9 (a). En la Figura 9 (b), hemos dibujado la gráfica de y = −x + 3. Tenga en cuenta que las gráficas coinciden cuando x < 3. En efecto, al considerar la rama izquierda de la “V” en la Figura 9 (a), se puede ver que la pendiente de esta rama es −1 y la intercepción y es 3. La ecuación de esta rama es y = −x+3, por lo que concuerda con la gráfica de y = −x+3 en la Figura 9 (b) cuando x es menor que 3.
Ejercicio\(\PageIndex{1}\)
Use una calculadora para aproximar primero\(\sqrt{2}\sqrt{5}\). Una la misma pantalla, aproximada\(\sqrt{10}\). Reporta los resultados en tu trabajo de tarea.
Ejercicio\(\PageIndex{2}\)
Use una calculadora para aproximar primero\(\sqrt{7}\sqrt{10}\). Una la misma pantalla, aproximada\(\sqrt{70}\). Reporta los resultados en tu trabajo de tarea.
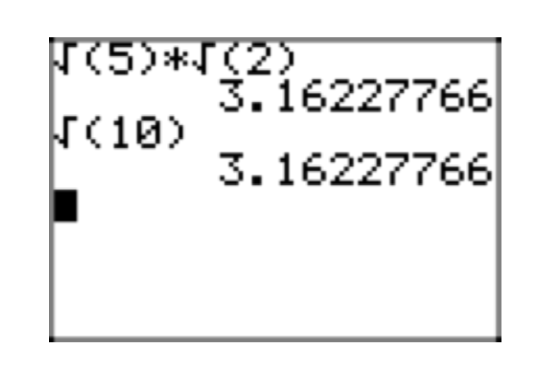
Ejercicio\(\PageIndex{3}\)
Use una calculadora para aproximar primero\(\sqrt{3}\sqrt{11}\). Una la misma pantalla, aproximada\(\sqrt{33}\). Reporta los resultados en tu trabajo de tarea.
Ejercicio\(\PageIndex{4}\)
Use una calculadora para aproximar primero\(\sqrt{5}\sqrt{13}\). Una la misma pantalla, aproximada\(\sqrt{65}\). Reporta los resultados en tu trabajo de tarea.
En los Ejercicios 5 - 20, coloque cada una de las expresiones radicales en forma radical simple. Al igual que en el Ejemplo 3 en la narrativa, verifica tu resultado con tu calculadora.
Ejercicio\(\PageIndex{5}\)
\(\sqrt{18}\)
- Contestar
-
\(\sqrt{18} = \sqrt{3^{2} \cdot 2}= \sqrt{3^{2}}\sqrt{2}=3\sqrt{2}\)
Ejercicio\(\PageIndex{6}\)
\(\sqrt{80}\)
Ejercicio\(\PageIndex{7}\)
\(\sqrt{112}\)
- Contestar
-
\(\sqrt{112} = \sqrt{4^{2} \cdot 7}= \sqrt{4^{2}}\sqrt{7}=4\sqrt{7}\)
Ejercicio\(\PageIndex{8}\)
\(\sqrt{72}\)
Ejercicio\(\PageIndex{9}\)
\(\sqrt{108}\)
- Contestar
-
\(\sqrt{108} = \sqrt{6^{2} \cdot 3}= \sqrt{6^{2}}\sqrt{3}=6\sqrt{3}\)
Ejercicio\(\PageIndex{10}\)
\(\sqrt{54}\)
Ejercicio\(\PageIndex{11}\)
\(\sqrt{50}\)
- Contestar
-
\(\sqrt{50} = \sqrt{5^{2} \cdot 2}= \sqrt{5^{2}}\sqrt{2}=5\sqrt{2}\)
Ejercicio\(\PageIndex{12}\)
\(\sqrt{48}\)
Ejercicio\(\PageIndex{13}\)
\(\sqrt{245}\)
- Contestar
-
\(\sqrt{245} = \sqrt{7^{2} \cdot 5}= \sqrt{7^{2}}\sqrt{5}=7\sqrt{5}\)
Ejercicio\(\PageIndex{14}\)
\(\sqrt{150}\)
Ejercicio\(\PageIndex{15}\)
\(\sqrt{98}\)
- Contestar
-
\(\sqrt{98} = \sqrt{7^{2} \cdot 2}= \sqrt{7^{2}}\sqrt{2}=7\sqrt{2}\)
Ejercicio\(\PageIndex{16}\)
\(\sqrt{252}\)
Ejercicio\(\PageIndex{17}\)
\(\sqrt{45}\)
- Contestar
-
\(\sqrt{45} = \sqrt{3^{2} \cdot 5}= \sqrt{3^{2}}\sqrt{5}=3\sqrt{5}\)
Ejercicio\(\PageIndex{18}\)
\(\sqrt{294}\)
Ejercicio\(\PageIndex{19}\)
\(\sqrt{24}\)
- Contestar
-
\(\sqrt{24} = \sqrt{2^{2} \cdot 6}= \sqrt{2^{2}}\sqrt{6}=2\sqrt{6}\)
Ejercicio\(\PageIndex{20}\)
\(\sqrt{32}\)
En los Ejercicios 21 - 26, usa la factorización prima (como en el Ejemplo 10 y 11 en la narrativa) para ayudarle a colocar la expresión radical dada en forma radical simple. C Diablos tu resultado con tu calculadora.
Ejercicio\(\PageIndex{21}\)
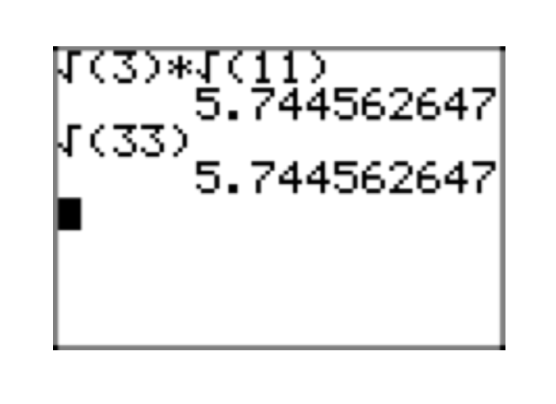
\(\sqrt{2016}\)
- Contestar
-
Tenga en cuenta que 2+0+1+6 = 9, que es divisible por 9. Así, 2016 es divisible por 9. En efecto,
\(2019 = 9 \cdot 224\)
Los dos últimos dígitos de 224 son 24, que es divisible por 4. Así, 224 es divisible por 4. Efectivamente,\(224 = 4 \cdot 56\).
\(2016 = 9 \cdot 224 = (3 \cdot 3) \cdot (4 \cdot 56)\).
Continuar a los cebos.
\(2016=3 \cdot 3 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 7 = 2^{5} \cdot 3^{2} \cdot 7\).
Comprobando,
Ejercicio\(\PageIndex{22}\)
\(\sqrt{2700}\)
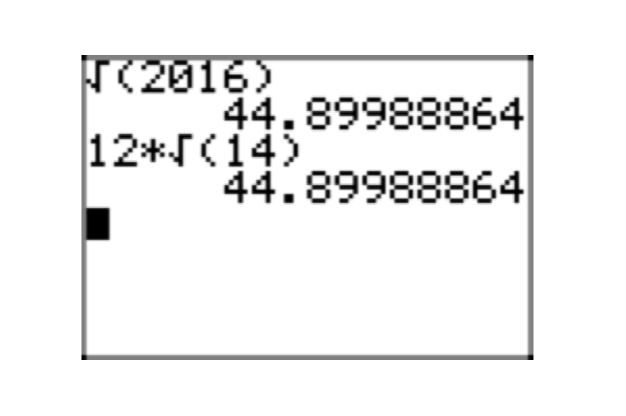
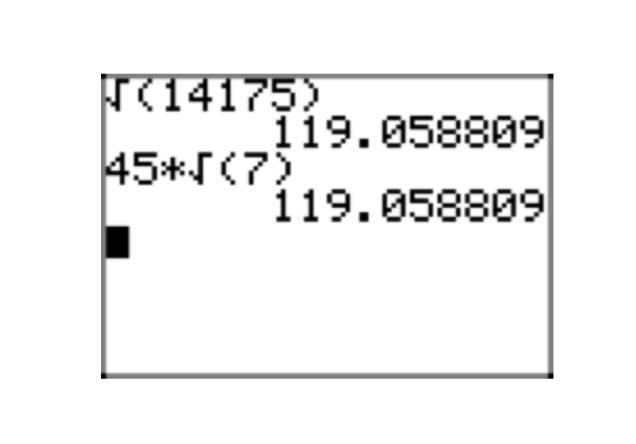
Ejercicio\(\PageIndex{23}\)
\(\sqrt{14175}\)
- Contestar
-
¡Dinero! Todo lo que termine en 00, 25, 50 o 75 es divisible por 25. Efectivamente,\(14175 = 25 \cdot 567\). Además, 5+6+7 = 18, entonces 567 es divisible por 9; es decir,\(567 = 9 \cdot 63\). Continuando con los primos,
\(14175 = 25 \cdot 567 = 5 \cdot 5 \cdot 9 \cdot 63 = 5 \cdot 5 \cdot 3 \cdot 3 \cdot 3 \cdot 3 \cdot 7\).
Factorizar nuestro un cuadrado perfecto (exponentes divisibles por 2).
\(\sqrt{14175} = \sqrt{3^{4} \cdot 5^{2}} \cdot \sqrt{7} = 3^{2} \cdot 5\sqrt{7} = 45\sqrt{7}\)
Comprobando,
Ejercicio\(\PageIndex{24}\)
\(\sqrt{44000}\)
Ejercicio\(\PageIndex{25}\)
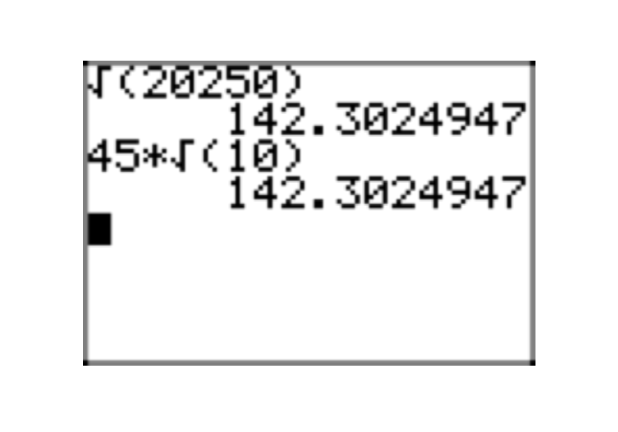
\(\sqrt{20250}\)
- Contestar
-
¡Dinero! Todo lo que termine en 00, 25, 50 o 75 es divisible por 25. Efectivamente,\(20250 = 25 \cdot 810\). Continuando con los primos,
\(20250 = 5 \cdot 5 \cdot 9 \cdot 9 \cdot 10 = 5 \cdot 5 \cdot 3 \cdot 3 \cdot 3 \cdot 3 \cdot 2 \cdot 5\).
Facturar un cuadrado perfecto.
\(\sqrt{20250} = \sqrt{2 \cdot 3^{4} \cdot 5^{3}} = \sqrt{3^{4} \cdot 5^{2}} \cdot \sqrt{2 \cdot 5} = 3^{2} \cdot 5 \sqrt{2 \cdot 5}=45\sqrt{10}\)
Comprobando,
Ejercicio\(\PageIndex{26}\)
\(\sqrt{3564}\)
En los Ejercicios 27 - 46, coloque cada una de las expresiones radicales dadas en forma radical simple. No hacer suposiciones sobre el signo de las variables. Las variables pueden representar números positivos o negativos.
Ejercicio\(\PageIndex{27}\)
\(\sqrt{(6x−11)^4}\)
- Contestar
-
\(\sqrt{(6x−11)^4} = \sqrt{((6x−11)^2)^2} = |(6x−11)^2|\)
Sin embargo, ya no\((6x − 11)^2\) es negativo, por lo que las barras de valor absoluto son innecesarias. Por lo tanto,
\(\sqrt{(6x−11)^4} = (6x−11)^2\)
Ejercicio\(\PageIndex{28}\)
\(\sqrt{16h^8}\)
Ejercicio\(\PageIndex{29}\)
\(\sqrt{25f^2}\)
- Contestar
-
\(\sqrt{25f^2} = \sqrt{25}\sqrt{f^2} = 5|f|\)
Debido a que f puede ser cualquier número real, no podemos eliminar las barras de valor absoluto sin más información.
Ejercicio\(\PageIndex{30}\)
\(\sqrt{25j^8}\)
Ejercicio\(\PageIndex{31}\)
\(\sqrt{16m^2}\)
- Contestar
-
\(\sqrt{16m^2} = \sqrt{4^{2}m^2} = \sqrt{4^2}\sqrt{m^2} = 4|m|\)
Dado que el índice en el radical es par y, después de la simplificación, la variable se eleva a una potencia impar, son necesarios signos de valor absoluto alrededor de la variable simplificada.
Ejercicio\(\PageIndex{32}\)
\(\sqrt{25a^2}\)
Ejercicio\(\PageIndex{33}\)
\(\sqrt{(7x+5)^{12}}\)
- Contestar
-
\(\sqrt{(7x+5)^{12}} = \sqrt{((7x+5)^6)^2} = |(7x+5)^6|\)
Sin embargo, ya no\((7x+5)^6\) es negativo, por lo que los signos de valor absoluto son innecesarios.
\(\sqrt{(7x+5)^{12}} = (7x+5)^6\)
Ejercicio\(\PageIndex{34}\)
\(\sqrt{9w^{10}}\)
Ejercicio\(\PageIndex{35}\)
\(\sqrt{25x^2−50x+25}\)
- Contestar
-
\(\sqrt{25x^2−50x+25}=\sqrt{(5x−5)^2} =|5x−5|\)
Debido a que x puede ser cualquier número real, los signos de valor absoluto alrededor del binomio simplificado son necesarios.
Ejercicio\(\PageIndex{36}\)
\(\sqrt{49x^2−42x+9}\)
Ejercicio\(\PageIndex{37}\)
\(\sqrt{25x^2+90x+81}\)
- Contestar
-
\(\sqrt{25x^2+90x+81} = \sqrt{(5x+9)^2} = |5x+9|\)
Debido a que x puede ser cualquier número real, los signos de valor absoluto alrededor del binomio simplificado son necesarios.
Ejercicio\(\PageIndex{38}\)
\(\sqrt{25f^{14}}\)
Ejercicio\(\PageIndex{39}\)
\(\sqrt{(3x+6)^{12}}\)
- Contestar
-
\(\sqrt{(3x+6)^{12}} = \sqrt{((3x+6)^6)^2} = |(3x+6)^6|\)
Sin embargo, la expresión ya\((3x+6)^6\) es no negativa, por lo que las barras de valor absoluto son innecesarias.
\(\sqrt{(3x+6)^{12}} = (3x+6)^6\)
Ejercicio\(\PageIndex{40}\)
\(\sqrt{(9x−8)^{12}}\)
Ejercicio\(\PageIndex{41}\)
\(\sqrt{36x^2+36x+9}\)
- Contestar
-
\(\sqrt{36x^2+36x+9} = \sqrt{(6x+3)^2} =|6x+3|\)
Debido a que x puede ser cualquier número real, los signos de valor absoluto alrededor del binomio simplificado son necesarios.
Ejercicio\(\PageIndex{42}\)
\(\sqrt{4e^2}\)
Ejercicio\(\PageIndex{43}\)
\(\sqrt{4p^{10}}\)
- Contestar
-
\(\sqrt{4p^{10}} = \sqrt{4}\sqrt{(p^5)^2}=2|p^5|\)
Ahora, podemos usar la propiedad multiplicativa de los valores absolutos y escribir
\(2|p^5| = 2|p^4||p| = 2p^{4}|p|\).
Dado que p puede ser cualquier número real, son necesarios signos de valor absoluto alrededor de la variable simplificada.
Ejercicio\(\PageIndex{44}\)
\(\sqrt{25x^{12}}\)
Ejercicio\(\PageIndex{45}\)
\(\sqrt{25q^6}\)
- Contestar
-
\(\sqrt{25q^6} = \sqrt{25}\sqrt{(q^3)^2} = 5|q^3|\)
Ahora, podemos usar la propiedad multiplicativa de los valores absolutos y escribir
\(5|q^3| = 5|q^2||q| = 5q^{2}|q|\).
Debido a que q puede ser cualquier número real, son necesarios signos de valor absoluto alrededor de la variable simplificada.
Ejercicio\(\PageIndex{46}\)
\(\sqrt{16h^{12}}\)
Ejercicio\(\PageIndex{47}\)
Dado que x < 0, coloque la expresión radical\(\sqrt{32x^6}\) en forma radical simple. Verifique su solución en su calculadora para x = −2.
- Contestar
-
Facturar un cuadrado perfecto.
\(\sqrt{32x^6} = \sqrt{16x^6}\sqrt{2} = \sqrt{16}\sqrt{x^6}\sqrt{2}=4|x^3|\sqrt{2}\)
Sin embargo,\(|x^3| = |x^2||x| = x^2|x|\), ya que\(x^2 \ge 0\). Así
\(\sqrt{32x^6} = 4x^{2}|x|\sqrt{2}\).
Si x < 0, entonces |x| = −x y
\(\sqrt{32x^6} = 4x^{2}(−x)\sqrt{2} =−4x^{3}\sqrt{2}\).
Comprobando con x = − 2.
Ejercicio\(\PageIndex{48}\)
Dado que x < 0, coloque la expresión radical\(\sqrt{54x^8}\) en forma radical simple. Verifique su solución en su calculadora para x = −2.
Ejercicio\(\PageIndex{49}\)
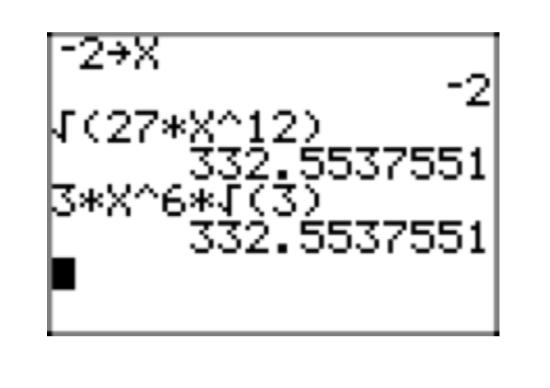
Dado que x < 0, coloque la expresión radical\(\sqrt{27x^{12}}\) en forma radical simple. Verifique su solución en su calculadora para x = −2.
Ejercicio\(\PageIndex{50}\)
Dado que x < 0, coloque la expresión radical\(\sqrt{44x^{10}}\) en forma radical simple. Verifique su solución en su calculadora para x = −2.
En los Ejercicios 51 - 54, sigue el ejemplo del Ejemplo 17 en la narrativa para simplificar la expresión radical dada y verificar tu resultado con tu graficación calcula tor.
Ejercicio\(\PageIndex{51}\)
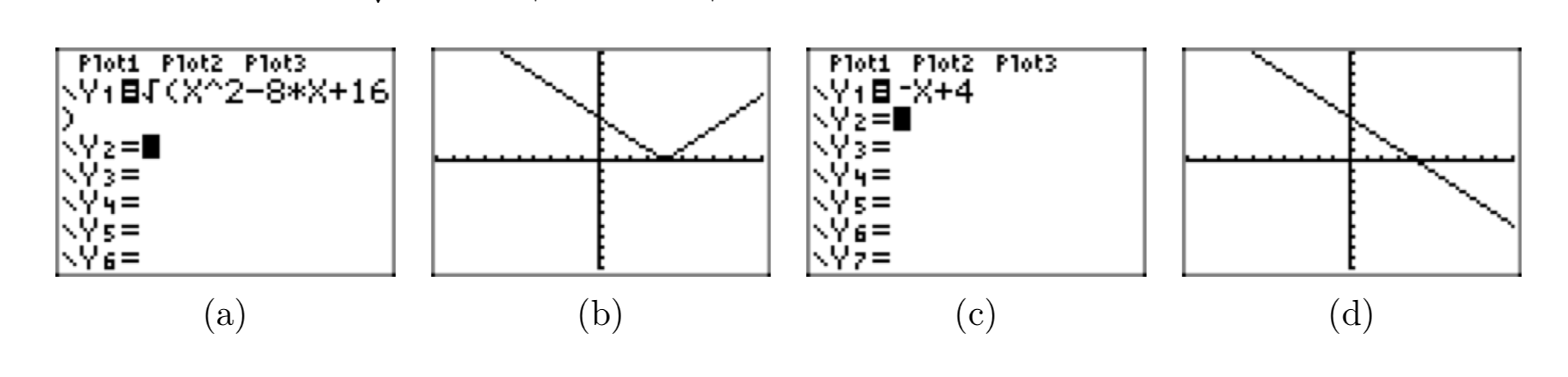
Dado que x < 4, colocar la expresión radical\(\sqrt{x^2−8x+16}\) en forma radical simple. Use una calculadora gráfica para mostrar que las gráficas de la expresión original y su forma radical simple concuerdan para todos los valores de x tal que x < 4.
- Contestar
-
Facturar el trinomio cuadrado perfecto.
\(\sqrt{x^2−8x+16} = \sqrt{(x−4)^2} =|x−4|\)
Si x < 4, o equivalentemente, si x−4 < 0, entonces |x−4| = − (x−4). Por lo tanto,
\(\sqrt{x^2−8x+16} =−x+4\).
En (b), hemos dibujado la gráfica de\(y = \sqrt{x^2−8x+16}\). En (d), hemos dibujado la gráfica de y = −x+4. Obsérvese que las gráficas en (b) y (d) coinciden cuando x < 4, lo que lleva credencial al hecho de que\(\sqrt{x^2−8x+16} =−x+4\) cuando x < 4.
Ejercicio\(\PageIndex{52}\)
Dado eso\(x \ge −2\), colocar la expresión radical\(\sqrt{x^2+4x+4}\) en forma radical simple. Use una calculadora gráfica para mostrar que las gráficas de la expresión original y su forma radical simple concuerdan para todos los valores de x tal que\(x \ge −2\).
Ejercicio\(\PageIndex{53}\)
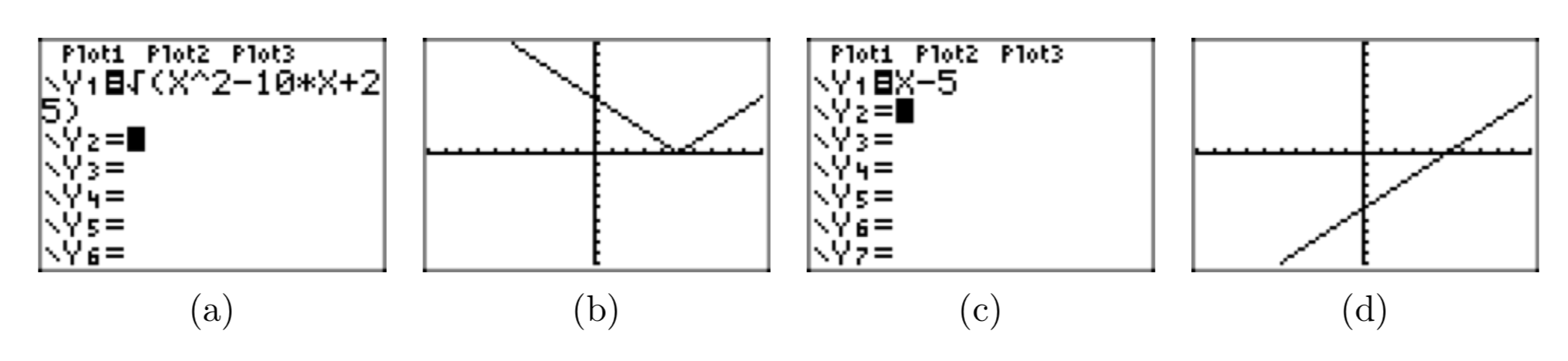
Dado eso\(x \ge 5\), colocar la expresión radical\(\sqrt{x^2−10x+25}\) en forma radical simple. Use una calculadora gráfica para mostrar que las gráficas de la expresión original y su forma radical simple concuerdan para todos los valores de x tal que\(x \ge 5\).
- Contestar
-
Facturar el trinomio cuadrado perfecto.
\(\sqrt{x^2−10x+25} = \sqrt{(x−5)^2} =|x−5|\)
Si\(x \ge 5\), o equivalentemente, si\(x−5 \ge 0\), entonces |x−5| = x−5. Por lo tanto,
\(\sqrt{x^2−8x+16} =x−5\).
En (b), hemos dibujado la gráfica de\(y = \sqrt{x^2−10x+25}\). En (d), hemos dibujado la gráfica de y = x−5. Obsérvese que las gráficas en (b) y (d) concuerdan cuando\(x \ge 5\), llevando credencial al hecho de que\(\sqrt{x^2−10x+25} = x−5\) cuando\(x \ge 5\).
Ejercicio\(\PageIndex{54}\)
Dado que x < −1, coloque la expresión radical\(\sqrt{x^2+2x+1}\) en forma radical simple. Use una calculadora gráfica para mostrar que las gráficas de la expresión original y su forma radical simple están de acuerdo para todos los valores de x tal que x < −1.
En los Ejercicios 55 - 72, colocar cada expresión radical en forma radical simple. Supongamos que todas las variables representan números positivos.
Ejercicio\(\PageIndex{55}\)
\(\sqrt{9d^{13}}\)
- Contestar
-
\(\sqrt{9d^{13}} = \sqrt{9}\sqrt{d^{12}}\sqrt{d}=3d^6\sqrt{d}\)
Ejercicio\(\PageIndex{56}\)
\(\sqrt{4k^2}\)
Ejercicio\(\PageIndex{57}\)
\(\sqrt{25x^2+40x+16}\)
- Contestar
-
\(\sqrt{25x^2+40x+16} = \sqrt{(5x+4)^2} = 5x+4\)
Ejercicio\(\PageIndex{58}\)
\(\sqrt{9x^2−30x+25}\)
Ejercicio\(\PageIndex{59}\)
\(\sqrt{4j^{11}}\)
- Contestar
-
\(\sqrt{4j^{11}} = \sqrt{4}\sqrt{j^{10}}\sqrt{j}=3j^5\sqrt{j}\)
Ejercicio\(\PageIndex{60}\)
\(\sqrt{16j^6}\)
Ejercicio\(\PageIndex{61}\)
\(\sqrt{25m^2}\)
- Contestar
-
\(\sqrt{25m^2} = \sqrt{25}\sqrt{m^2} = 5m\)
Ejercicio\(\PageIndex{62}\)
\(\sqrt{9e^9}\)
Ejercicio\(\PageIndex{63}\)
\(\sqrt{4c^5}\)
- Contestar
-
\(\sqrt{4c^5} = \sqrt{4c^4}\sqrt{c} = 2c^{2}\sqrt{c}\)
Ejercicio\(\PageIndex{64}\)
\(\sqrt{25z^2}\)
Ejercicio\(\PageIndex{65}\)
\(\sqrt{25h^{10}}\)
- Contestar
-
\(\sqrt{25h^{10}} = \sqrt{25}\sqrt{h^{10}} = 5h^5\)
Ejercicio\(\PageIndex{66}\)
\(\sqrt{25b^2}\)
Ejercicio\(\PageIndex{67}\)
\(\sqrt{9s^7}\)
- Contestar
-
\(\sqrt{9s^7} = \sqrt{9s^6}\sqrt{s} = 3s^{3}\sqrt{s}\)
Ejercicio\(\PageIndex{68}\)
\(\sqrt{9e^7}\)
Ejercicio\(\PageIndex{69}\)
\(\sqrt{4p^8}\)
- Contestar
-
\(\sqrt{4p^8} = \sqrt{4}\sqrt{p^8} = 2\sqrt{p^4}\)
Ejercicio\(\PageIndex{70}\)
\(\sqrt{9d^{15}}\)
Ejercicio\(\PageIndex{71}\)
\(\sqrt{9q^{10}}\)
- Contestar
-
\(\sqrt{9q^{10}} = \sqrt{9}\sqrt{q^{10}} = 3\sqrt{q^5}\)
Ejercicio\(\PageIndex{72}\)
\(\sqrt{4w^7}\)
En los Ejercicios 73 - 80, coloque cada expresión radical dada en forma radical simple. Supongamos que todas las variables representan números positivos.
Ejercicio\(\PageIndex{73}\)
\(\sqrt{2f^5}\sqrt{8f^3}\)
- Contestar
-
\(\sqrt{2f^5}\sqrt{8f^3} =\sqrt{2 \cdot 8 \cdot f^5 \cdot f^3} = \sqrt{16f^8} = \sqrt{16}\sqrt{(f^4)^2} =4f^4\)
Ejercicio\(\PageIndex{74}\)
\(\sqrt{3s^3}\sqrt{243s^3}\)
Ejercicio\(\PageIndex{75}\)
\(\sqrt{2k^7}\sqrt{32k^3}\)
- Contestar
-
\(\sqrt{2k^7}\sqrt{32k^3} = \sqrt{2 \cdot 32 \cdot k^7 \cdot k^3} = \sqrt{64k^{10}} = \sqrt{64}\sqrt{(k^5)^2}=8k^5\)
Ejercicio\(\PageIndex{76}\)
\(\sqrt{2n^9}\sqrt{8n^3}\)
Ejercicio\(\PageIndex{77}\)
\(\sqrt{2e^9}\sqrt{8e^3}\)
- Contestar
-
\(\sqrt{2e^9}\sqrt{8e^3} = \sqrt{2 \cdot 8 \cdot e^9 \cdot e^3} = \sqrt{16e^{12}} = \sqrt{16}\sqrt{(e^6)^2}=4e^6\)
Ejercicio\(\PageIndex{78}\)
\(\sqrt{5n^9}\sqrt{125n^3}\)
Ejercicio\(\PageIndex{79}\)
\(\sqrt{3z^5}\sqrt{27z^3}\)
- Contestar
-
\(\sqrt{3z^5}\sqrt{27z^3} = \sqrt{3 \cdot 27 \cdot z^5 \cdot z^3} = \sqrt{81z^8} = \sqrt{81}\sqrt{(z^4)^2}=9z^4\)
Ejercicio\(\PageIndex{80}\)
\(\sqrt{3t^7}\sqrt{27t^3}\)