9.6: El teorema de Pitágoras

Pitágoras fue un matemático y filósofo griego, nacido en la isla de Samos (ca. 582 a.C.). Fundó varias escuelas, una en particular en una ciudad del sur de Italia llamada Crotone, cuyos miembros finalmente se conocieron como los pitagóricos. El círculo íntimo de la escuela, el Mathematikoi, vivía en la escuela, se libraba de todas las posesiones personales, eran vegetarianos y observaban un estricto voto de silencio. Estudiaron matemáticas, filosofía y música, y sostenían la creencia de que los números constituyen la verdadera naturaleza de las cosas, dando a los números una cualidad mística o incluso espiritual.

Hoy no se sabe nada de los escritos de Pitágoras, quizás por el secreto y el silencio de la sociedad pitagórica. Sin embargo, uno de los teoremas más famosos de todas las matemáticas sí lleva su nombre, el Teorema de Pitágoras.

TEORMA DE PITAGORAS

Que c represente la longitud de la hipotenusa, el lado de un triángulo rectángulo directamente opuesto al ángulo recto (un ángulo recto mide 90º) del triángulo. Los lados restantes del triángulo rectángulo se denominan patas del triángulo rectángulo, cuyas longitudes están designadas por las letras a y b.

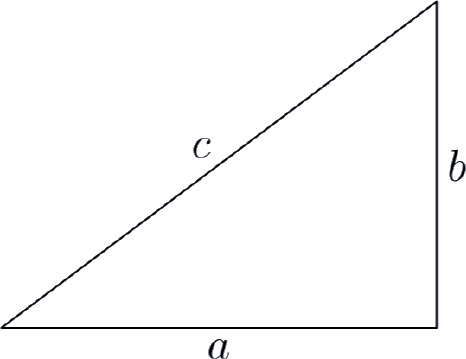
La relación que involucra las piernas y la hipotenusa del triángulo rectángulo, dada por

\[a^2 + b^2 = c^2 \label{1}\]

se llama Teorema de Pitágoras.

Tenga en cuenta que el Teorema de Pitágoras solo se puede aplicar a los triángulos rectos. Veamos una sencilla aplicación del Teorema de Pitágoras (Equat ion\ ref {1}).

Ejemplo\(\PageIndex{2}\)

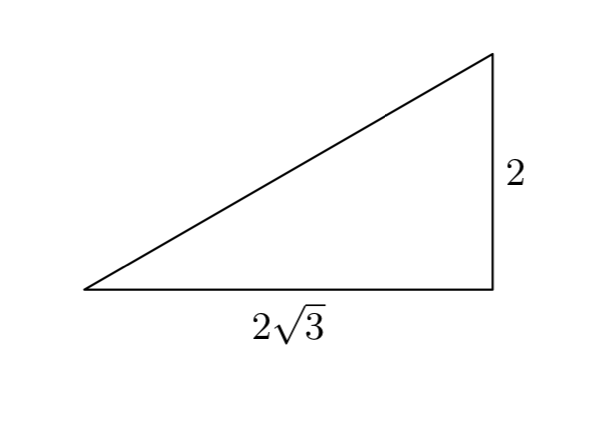
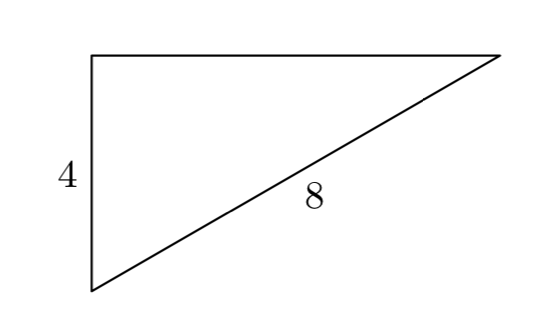
Dado que la longitud de una pata de un triángulo rectángulo es de 4 centímetros y la hipotenusa tiene una longitud de 8 centímetros, encuentra la longitud del segundo tramo.

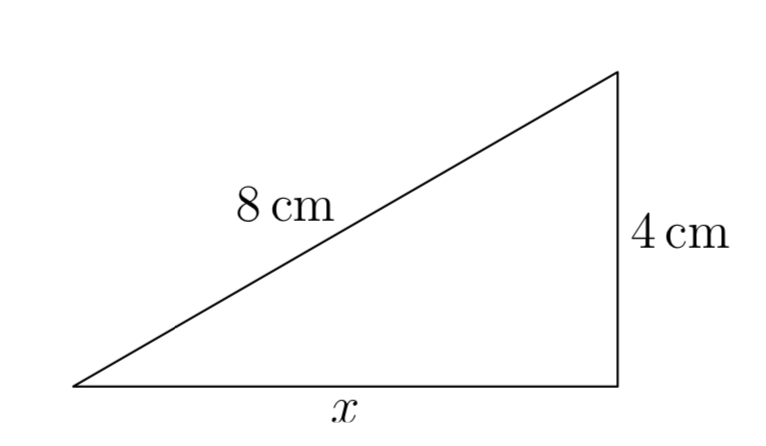
Empecemos por bosquejar y etiquetar un triángulo rectángulo con la información dada. Dejaremos que x represente la longitud de la pierna faltante.

Figura 1. Un boceto facilita un poco las cosas

Aquí hay un consejo importante.

TIP\(\PageIndex{3}\): Hypotenuse

La hipotenusa es el lado más largo del triángulo rectángulo. Se encuentra directamente enfrente del ángulo recto del triángulo. Lo más importante es que es la cantidad que se aísla por sí misma en el Teorema de Pitágoras (Ecuación\ ref {1}). Siempre aísle la cantidad que representa la hipotenusa en un lado de la ecuación. Las “piernas” van del otro lado de la ecuación.

Entonces, tomando la punta al corazón, y anotando las longitudes de las piernas y la hipotenusa en la Figura 1, escribimos

\(4^2+x^2 = 8^2\).

Cuadrado, luego aísle x en un lado de la ecuación.

\(16+x^2 = 64\)

\(x^2 = 48\)

Normalmente, tomaríamos más o menos la raíz cuadrada para resolver esta ecuación, pero x representa la longitud de una pata, que debe ser un número positivo. De ahí que tomemos solo la raíz cuadrada positiva de 48.

\(x = \sqrt{48}\)

Por supuesto, coloca tu respuesta en forma radical simple.

\(x = \sqrt{16}\sqrt{3}\)

\(x = 4\sqrt{3}\)

Si es necesario, puede usar su calculadora gráfica para aproximar esta longitud. A la centésima de centímetro más cercana,\(x \approx 6.93\) centímetros.

Prueba del Teorema de Pitágoras

No se sabe si Pitágoras fue la primera en proporcionar una prueba del Teorema de Pitágoras. Muchos historiadores matemáticos piensan que no. En efecto, ni siquiera se sabe si Pitágoras confeccionó una prueba del teorema que lleva su nombre, y mucho menos fue el primero en aportar una prueba.

Existe evidencia de que los antiguos babilonios estaban al tanto del Teorema de Pitágoras más de 1000 años antes de la época de Pitágoras. Una tablilla de arcilla, ahora denominada Plimpton 322 (ver Figura 2), contiene ejemplos de Triples Pitágoras, conjuntos de tres números que satisfacen el Teorema de Pitágoras (como 3, 4, 5).

Figura 2. Una fotografía de Plimpton 322.

Una de las primeras pruebas registradas del Teorema de Pitágoras data de la dinastía Han (206 aC a 220 d.C.), y se registra en el Chou Pei Suan Ching (ver Figura 3). Se puede ver que esta figura aborda específicamente el caso del triángulo rectángulo 3, 4, 5. Los historiadores matemáticos están divididos en cuanto a si la imagen estaba destinada o no a formar parte de una prueba general o simplemente fue ideada para abordar este caso específico. También hay desacuerdo sobre si la prueba fue proporcionada por un comentarista más moderno o se remonta más atrás en el tiempo.

Figura 3. Una figura del Chou Pei Suan Ching

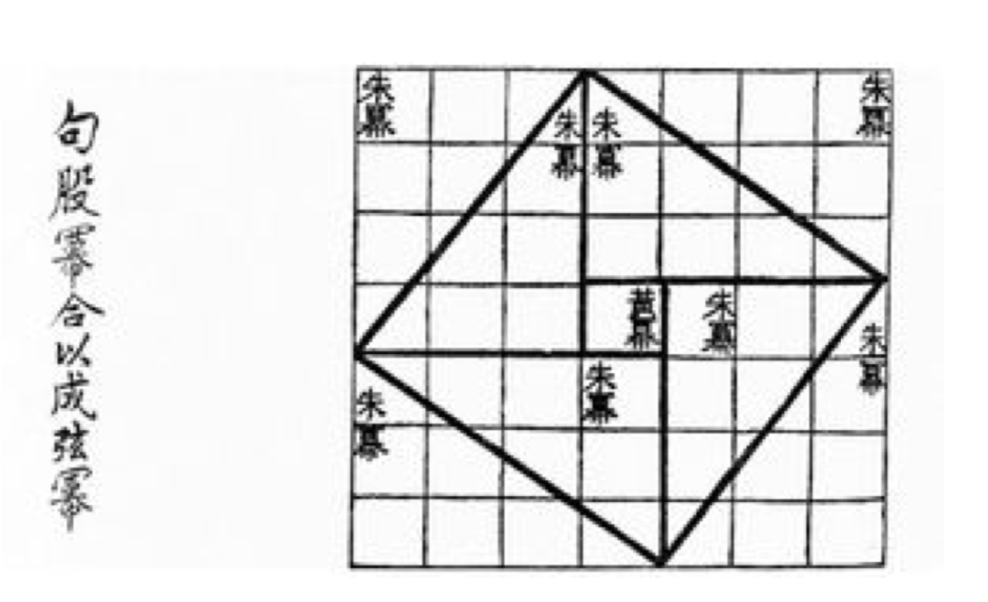
Sin embargo, la Figura 3 sugiere un camino que podríamos tomar en el camino hacia una prueba del Teorema de Pitágoras. Comience con un triángulo rectángulo arbitrario que tenga patas de longitudes a y b, e hipotenusa con longitud c, como se muestra en la Figura 4 (a).

A continuación, haga cuatro copias del triángulo mostrado en la Figura 4 (a), después rotarlas y trasladarlas a su lugar como se muestra en la Figura 4 (b). Tenga en cuenta que esto forma un cuadrado grande que es c unidades en un lado.

Además, la posición de los triángulos en la Figura 4 (b) permite la formación de un cuadrado menor, sin sombra en el centro del cuadrado mayor. No es difícil calcular la longitud del lado de este cuadrado más pequeño. Simplemente resta la longitud de la pierna más pequeña de la pata más grande del triángulo original. Así, el lado del cuadrado más pequeño tiene longitud b − a.

Figura 4. Prueba del Teorema de Pitágoras.

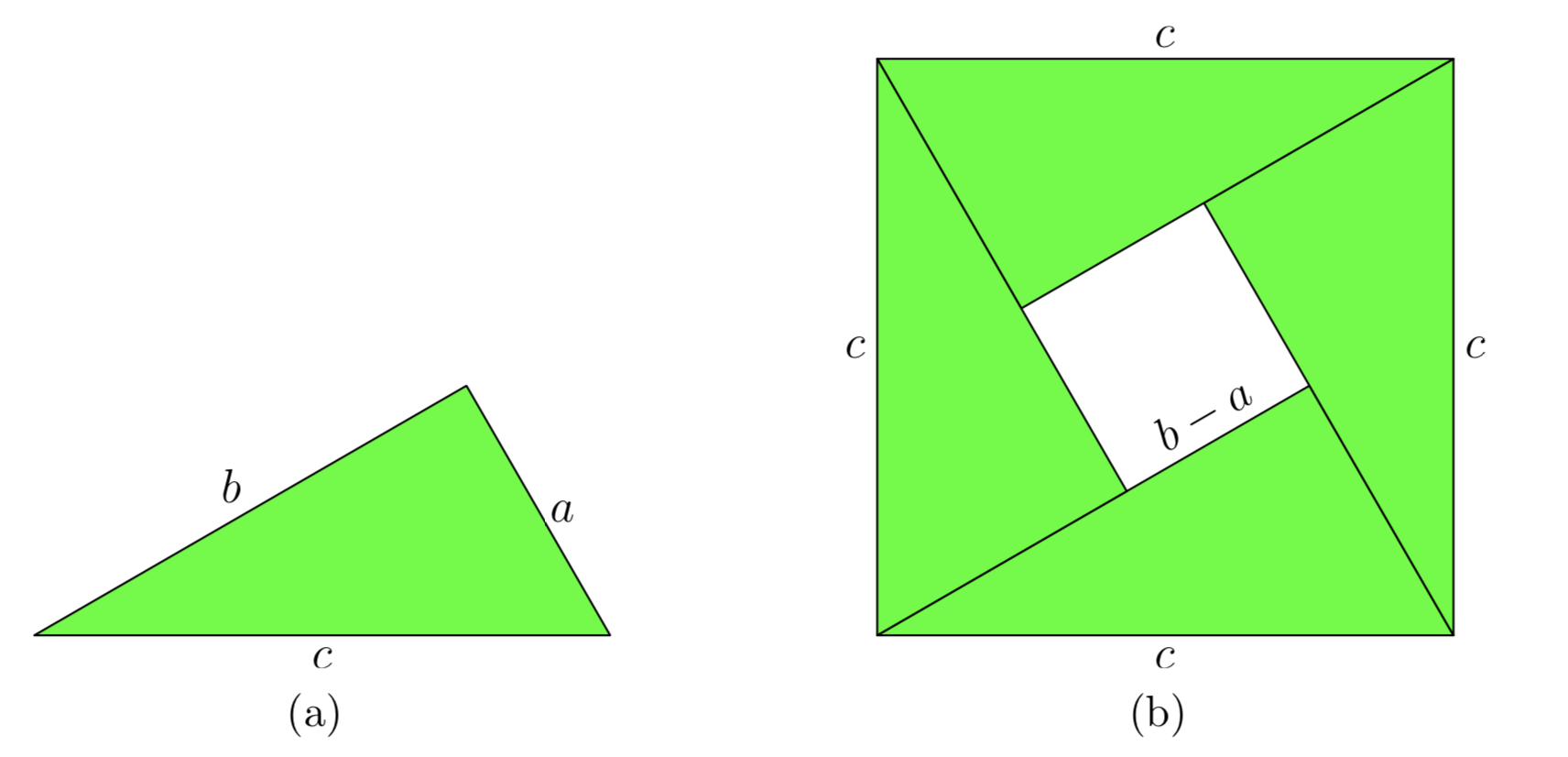
Ahora, calcularemos el área del cuadrado grande en la Figura 4 (b) de dos maneras separadas.

• Primero, el cuadrado grande en la Figura 4 (b) tiene un lado de longitud c. Por lo tanto, el área del cuadrado grande es

  \(Area = c^2\).

• En segundo lugar, el cuadrado grande de la Figura 4 (b) está formado por 4 triángulos del mismo tamaño y un cuadrado menor que tiene un lado de longitud b−a; podemos calcular el área del cuadrado grande sumando el área de los 4 triángulos y el cuadrado menor.

1. El área del cuadrado más pequeño es\((b−a)^2\).
2. El área de cada triángulo es\(\frac{ab}{2}\). De ahí que el área de cuatro triángulos de igual tamaño sea cuatro veces este número;

es decir,\(4(\frac{ab}{2})\). Así, el área de la plaza grande es

Área = Área de cuadrado pequeño +\(4 \cdot\) Área de triángulo

=\((b−a)^2+4(\frac{ab}{2})\).

Calculamos el área del cuadrado más grande dos veces. La primera vez que llegamos\(c^2\); la segunda vez que llegamos\((b−a)^2+4(\frac{ab}{2})\). Por lo tanto, estas dos cantidades deben ser iguales.

\(c^2 = (b−a)^2+4(\frac{ab}{2})\).

Ampliar el binomio y simplificar.

\(c^2 = b^2−2ab+a^2 +2ab\)

\(c^2 = b^2+a^2\)

Es decir,

\(a^2+b^2 = c^2\),

y se prueba el Teorema de Pitágoras.

Aplicaciones del Teorema de Pitágoras

En esta sección veremos algunas aplicaciones del Teorema de Pitágoras, uno de los teoremas más aplicados en todas las matemáticas. Solo pregúntale a tu carpintero local.

Los antiguos egipcios tomarían una cuerda con 12 nudos igualmente espaciados como la que se muestra en la Figura 5, y la usarían para cuadrar esquinas de sus edificios. La herramienta fue instrumental en la construcción de las pirámides.

Figura 5. Un triángulo rectángulo básico 3-4-5 para cuadrar esquinas.

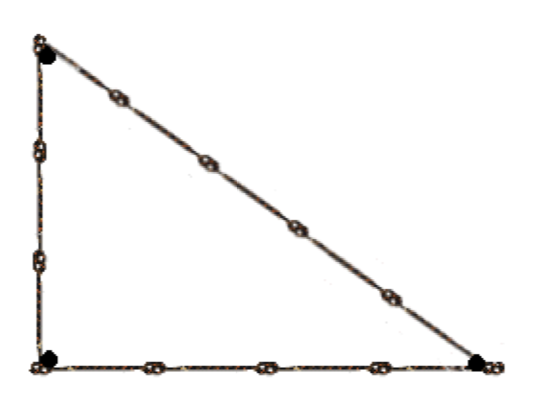
El teorema de Pitágoras también es útil en topografía, cartografía y navegación, por nombrar algunas posibilidades.

Veamos algunos ejemplos del Teorema de Pitágoras en acción.

Ejemplo\(\PageIndex{4}\)

Una pata de un triángulo rectángulo es 7 metros más larga que la otra pierna. La longitud de la hipotenusa es de 13 metros. Encuentra las longitudes de todos los lados del triángulo rectángulo.

Sea x representar la longitud de una pata del triángulo rectángulo. Debido a que el segundo tramo es 7 metros más largo que el primer tramo, la longitud del segundo tramo se puede representar por la expresión x + 7, como se muestra en la Figura 6, donde también hemos etiquetado la longitud de la hipotenusa (13 metros).

Figura 6. El segundo tramo es 7 metros más largo que el primero.

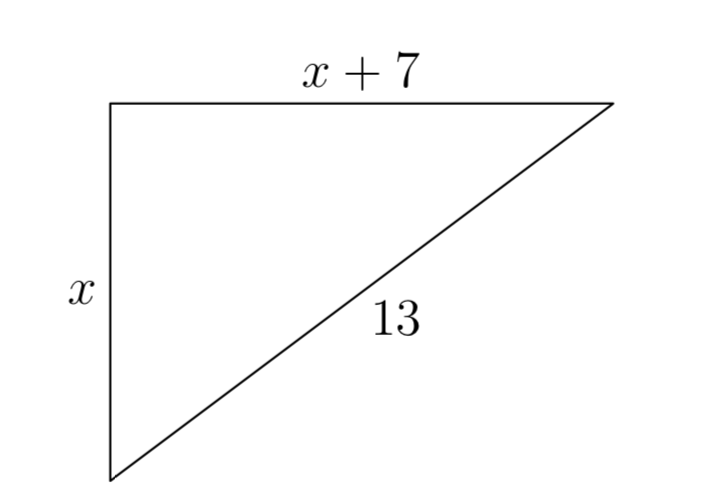
Recuerde aislar la longitud de la hipotenusa en un lado de la ecuación que representa el Teorema de Pitágoras. Es decir,

\(x^2+(x+7)^2 = 13^2\).

Tenga en cuenta que las piernas van en un lado de la ecuación, la hipotenusa en el otro. Cuadrado y simplificar. Recuerda usar el cuadriculado un patrón binomial.

\(x^2+x^2+14x+49 = 169\)

\(2x^2 +14x+49 = 169\)

Esta ecuación es no lineal, así que haz un lado cero restando 169 de ambos lados de la ecuación.

\(2x^2+14x+49−169 = 0\)

\(2x^2 +14x−120 = 0\)

Tenga en cuenta que cada término en el lado izquierdo de la ecuación es divisible por 2. Divide ambos lados de la ecuación por 2.

\(x^2+7x−60 = 0\)

Usemos la fórmula cuadrática con a = 1, b = 7 y c = −60.

\(x = \frac{−b \pm \sqrt{b^2−4ac}}{2a} = \frac{−7 \pm \sqrt{7^2 −4(1)(−60)}}{2(1)}\)

Simplificar.

\(x = \frac{−7 \pm \sqrt{289}}{2}\)

Tenga en cuenta que 289 es un cuadrado perfecto (\(17^2 = 289\)). Por lo tanto,

\(x = \frac{−7 \pm 17}{2}\).

Así, tenemos dos soluciones,

x = 5 o x = −12.

Debido a que la longitud debe ser un número positivo, eliminamos − 12 de la consideración. Así, la longitud del primer tramo es x = 5 metros. La longitud del segundo tramo es x +7, o 12 metros.

Cheque. Revisar es un asunto fácil. Las piernas son de 5 y 12 metros, respectivamente, y la hipotenusa es de 13 metros. Tenga en cuenta que el segundo tramo es 7 metros más largo que el primero. También,

\(5^2+12^2 = 25+144 = 169\),

que es el cuadrado de 13.

Los lados integrales del triángulo en el ejemplo anterior, 5, 12 y 13, son un ejemplo de una Triple pitagórica.

TRIPLE PITAGOREAN

Un conjunto de enteros positivos a, b y c, se llama Triple de Pitágoras si satisfacen el Teorema de Pitágoras; es decir, si

\(a^2+b^2 = c^2\).

Si el mayor factor común de a, b y c es 1, entonces el triple (a, b, c) se llama triple pitagórica primitiva.

Así, por ejemplo, la Triple Pitagórica (5, 12, 13) es primitiva. Veamos otro ejemplo.

Ejemplo\(\PageIndex{5}\)

Si (a, b, c) es un triple pitagórico, mostrar que cualquier múltiplo integral positivo es también un triple pitagórico.

Así, si los enteros positivos (a, b, c) es un Triple pitagórico, debemos demostrar que (ka, kb, kc), donde k es un entero positivo, es también un Triple pitagórico.

Sin embargo, sabemos que

\(a^2+b^2 = c^2\).

Multiplique ambos lados de esta ecuación por\(k^2\).

\(k^{2}a^2+k^{2}b^2 = k^{2}c^2\)

Este último resultado se puede escribir

\((ka)^2 + (kb)^2 = (kc)^2\).

De ahí que (ka, kb, kc) sea un Triple pitagórico.

De ahí que debido a que (3, 4, 5) es una Triple Pitagórica, se puede duplicar todo para obtener otra triple (6, 8, 10). Tenga en cuenta que\(6^2 + 8^2 = 10^2\) se verifica fácilmente. De igual manera, triplicar da otro triple (9, 12, 15), y así sucesivamente.

En el Ejemplo 5, mostramos que (5, 12, 13) era un triple, por lo que podemos tomar múltiplos para generar otras Triples pitagóricas, como (10, 24, 26) o (15, 36, 39), y así sucesivamente.

Las fórmulas para generar Triples Pitágoras se conocen desde la antigüedad.

Ejemplo\(\PageIndex{6}\)

La siguiente fórmula para generar Triples Pitágoras fue publicada en Euclides (325—265 a.C.) Elements, uno de los libros de texto más exitosos en la historia de las matemáticas. Si m y n son enteros positivos con m > n, mostrar

\(a = m^2−n^2\),

b = 2mn, (7)

\(c = m^2+n^2\),

genera Triples Pitagóricos.

Solo necesitamos demostrar que las fórmulas para a, b y c satisfacen al Theo rem pitagórico. Con eso es mente, primero calculemos\(a^2+b^2\).

\(a^2+b^2 = (m^2−n^2)^2+(2mn)^2\)

=\(m^4−2m^{2}n^{2}+n^4+4m^{2}n^2\)

=\(m^4+2m^{2}n^2+n^4\)

Por otra parte,

\(c^2 = (m^2+n^2)^2\)

=\(m^4+2m^{2}n^2+n^4\).
De ahí\(a^2+b^2 = c^2\),, y las expresiones para a, b, y c forman una Triple pitagórica.

Es interesante y divertido generar Triples pitagóricos con las fórmulas del Ejemplo 6. Elija m = 4 y n = 2, luego

\(a = m^2−n^2 = (4)^2−(2)^2 = 12\),

\(b = 2mn = 2(4)(2) = 16\),

\(c = m^2+n^2 =(4)^2+(2)^2 = 20\).

Es fácil comprobar que el triple (12, 16, 20) satisfará\(12^2+16^2 = 20^2\). En efecto, tenga en cuenta que este triple es un múltiplo del triple básico (3 , 4, 5), por lo que también debe ser un triple pitagórico.

También se puede demostrar que si m y n son relativamente primos, y no son ambos impares ni ambos pares, entonces las fórmulas del Ejemplo 6 generarán un Triple pitagórico primitivo. Por ejemplo, elija m = 5 y n = 2. Tenga en cuenta que el mayor divisor común de m = 5 y n = 2 es uno, por lo que m y n son relativamente primos. Además, m es impar mientras que n es par. Estos valores de m y n generan

\(a = m^2−n^2 = (5)^2−(2)^2 = 21\),

\(b = 2mn = 2(5)(2) = 20\),

\(c = m^2+n^2 = (5)^2+(2)^2 = 29\).

Tenga en cuenta que

\(21^2+20^2 = 441+400 = 841 = 29^2\).

De ahí que (21, 20, 29) sea una Triple pitagórica. Además, el mayor divisor común de 21, 20 y 29 es uno, por lo que (21, 20, 29) es primitivo.
Las aplicaciones prácticas del Teorema de Pitágoras son numerosas.

Ejemplo\(\PageIndex{8}\)

Un pintor apoya una escalera de 20 pies contra la pared de una casa. La base de la escalera se encuentra en terreno nivelado a 5 pies de la pared de la casa. ¿Qué tan alto llegará la escalera a la pared de la casa?

Considera el triángulo en la Figura 7. La hipotenusa del triángulo representa la escalera y tiene una longitud de 20 pies. La base del triángulo representa la distancia de la base de la escalera desde la pared de la casa y es de 5 pies de largo. La pata vertical del triángulo es la distancia que la escalera alcanza hasta la pared y la cantidad que deseamos determinar.

Figura 7. Una escalera se apoya contra la pared de una casa.

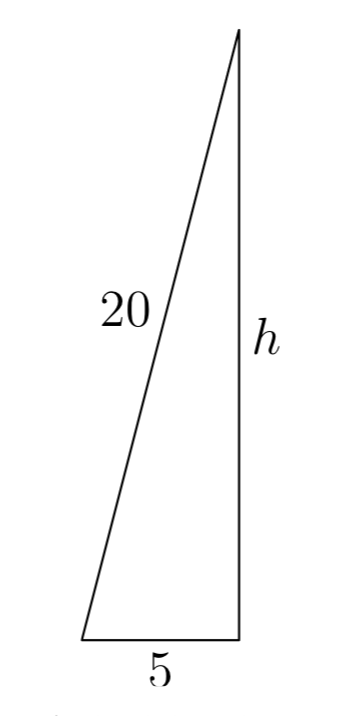
Aplicando el Teorema de Pitágoras,

\(5^2+h^2 = 20^2\).

Nuevamente, tenga en cuenta que el cuadrado de la longitud de la hipotenusa es la cantidad que se aísla en un lado de la ecuación.

A continuación, cuadrado, luego aislar el término que contiene h en un lado de la ecuación restando 25 de ambos lados de la ecuación resultante.

\(25+h^2 = 400\)

\(h^2 = 375\)

Solo necesitamos extraer la raíz cuadrada positiva.

\(h = \sqrt{375}\)

Podríamos colocar la solución en forma simple, es decir\(h = 5\sqrt{15}\), pero la naturaleza del problema justifica una aproximación decimal. Usando una calculadora y redondeando a la décima de pie más cercana,

\(h \approx 19.4\).

Así, la escalera alcanza aproximadamente 19.4 pies arriba de la pared.

La fórmula de distancia

Muchas veces necesitamos calcular la distancia entre dos puntos P y Q en el plano. En efecto, esta es una necesidad tan recurrente, nos gustaría desarrollar una fórmula que calcule rápidamente la distancia entre los puntos P y Q. Dicha fórmula es el objetivo de esta última sección.

Dejar que P (x1, y1) y Q (x2, y2) sean dos puntos arbitrarios en el plano, como se muestra en la Figura 8 (a) y dejar que d represente la distancia entre los dos puntos.

Figura 8. Encontrar la distancia entre los puntos P y Q.

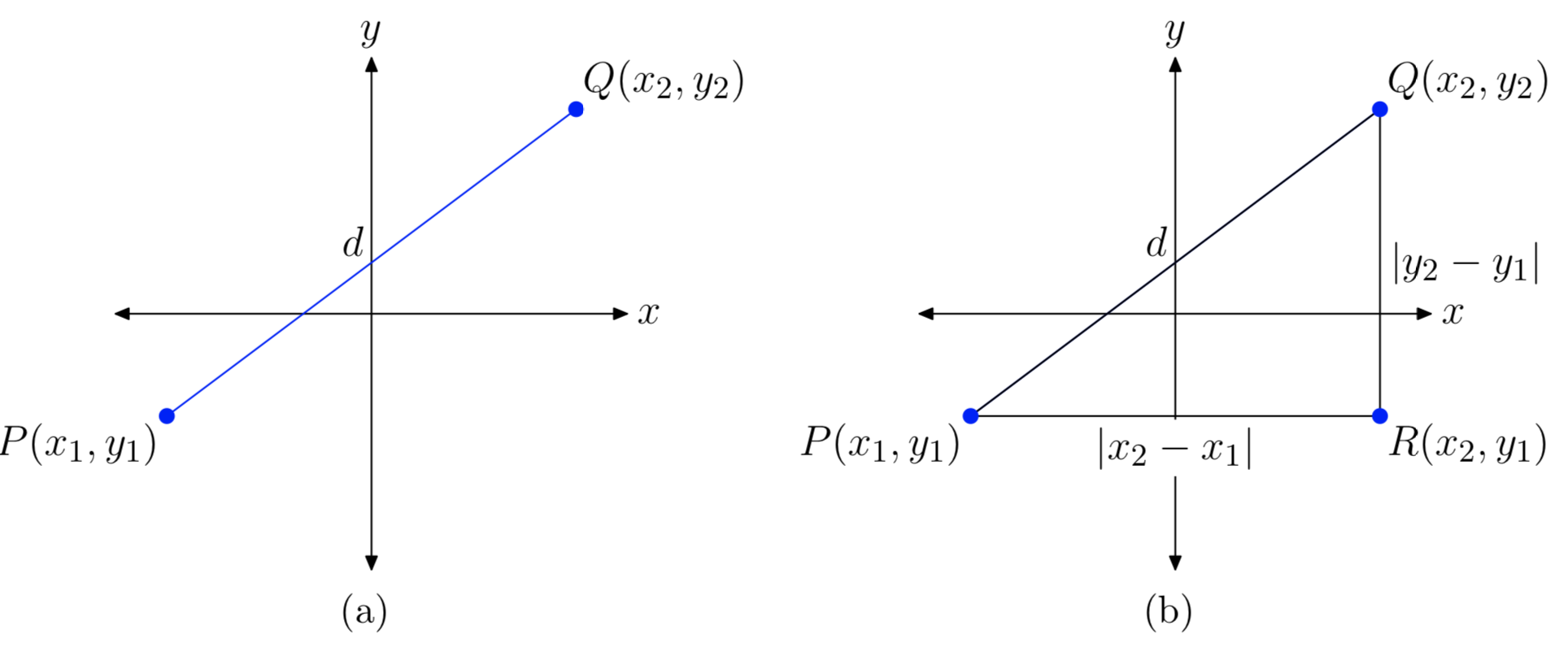
Para encontrar la distancia d, primero dibuje el triángulo rectángulo ∆PQR, con patas paralelas a los ejes, como se muestra en la Figura 8 (b). A continuación, necesitamos encontrar las longitudes de las patas del triángulo rectángulo ∆PQR.

• La distancia entre P y R se encuentra restando la coordenada x de P de la coordenada x de R y tomando el valor absoluto del resultado. Es decir, la distancia entre P y R es\(|x_{2}−x_{1}|\).
• La distancia entre R y Q se encuentra restando la coordenada y de R de la coordenada y de Q y tomando el valor absoluto del resultado. Es decir, la distancia entre R y Q es\(|y_{2}−y_{1}|\).

Ahora podemos usar el Teorema de Pitágoras para calcular d. Así,

\(d^2 = (|x_{2}−x_{1}|)^2+(|y_{2}−y_{1}|)^2\).

Sin embargo, para cualquier número real a,

\((|a|)^2 = |a|·|a| = |a^2| = a^2\),

porque a2 no es negativo. De ahí,\((|x_{2} − x_{1}|)^2 = (x_{2} − x_{1})^2 and (|y_{2} − y_{1}|)^2 = (y_{2} − y_{1})^2\) y podemos escribir

\(d^2 = (x_{2}−x_{1})^2+(y_{2}−y_{1})^2\).

Tomar la raíz cuadrada positiva conduce a la Fórmula de Distancia.

La fórmula a distancia

Sea P (x1, y1) y Q (x2, y2) dos puntos arbitrarios en el plano. La distancia d entre los puntos P y Q viene dada por la fórmula

\(d = \sqrt{(x_{2}−x_{1})^2+(y_{2}−y_{1})^2}\). (9)

La dirección de la resta no es importante. Debido a que cuadras el resultado de la resta, obtienes la misma respuesta independientemente de la dirección de la resta (por ejemplo,\((5 − 2)^2 = (2 − 5)^2\)). Thus, it doesn’t matter which point you designate as the punto P, ni importa qué punto designes como punto Q. Simplemente restar x - coordenadas y cuadrado, restar y -coordenadas y cuadrado, sumar, luego tomar la raíz cuadrada.

Veamos un ejemplo.

Ejemplo\(\PageIndex{10}\)

Encuentra la distancia entre los puntos P (−4, −2) y Q (4, 4).

Ayuda a la intuición si dibujamos un cuadro, como lo hemos hecho en la Figura 9. Ahora se puede tomar una brújula y abrirla a la distancia entre los puntos P y Q. Entonces puedes colocar tu brújula en el eje horizontal (o cualquier cuadrícula horizontal) para estimar la distancia entre los puntos P y Q. Lo hicimos en nuestro papel cuadriculado y estimamos la distancia\(d \approx 10\).

Figura 9. Graficando la distancia entre P (−4, −2) y Q (4, 4).

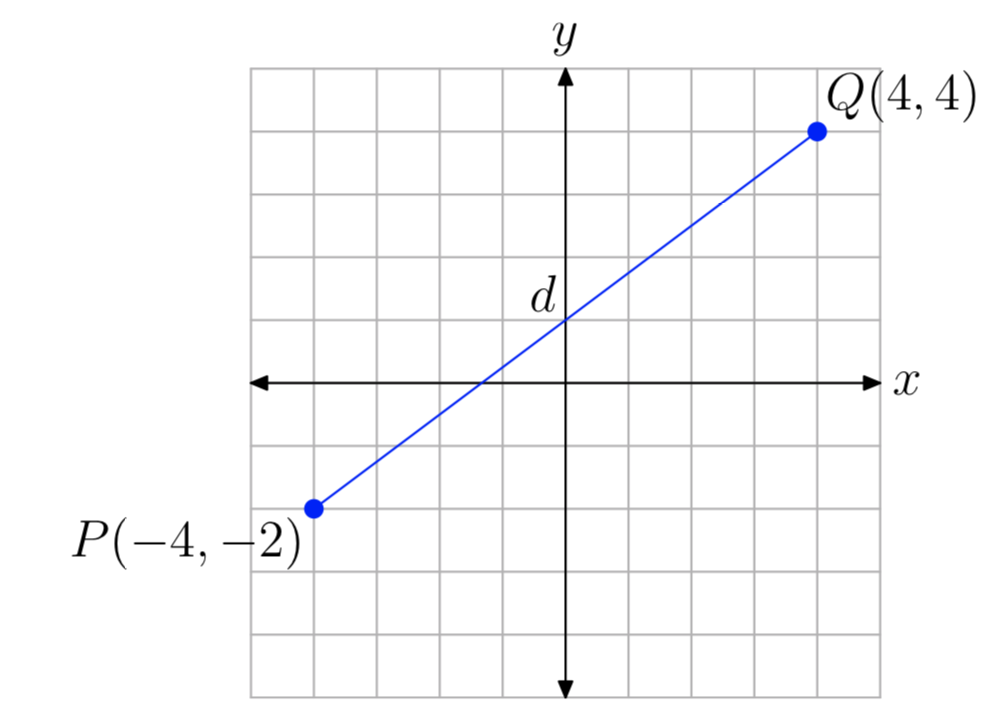
Ahora usemos la fórmula de distancia para obtener un valor exacto para la distancia d. con\((x_{1}, y_{1})\) = P (−4, −2) y\((x_{2}, y_{2})\) = Q (4, 4),

\(d = \sqrt{(x_{2}−x_{1})^2+(y_{2}−y_{1})^2}\)

=\(\sqrt{(4−(−4))^2+(4−(−2))^2}\)

=\(\sqrt{8^2+6^2}\)

=\(\sqrt{64+36}\)

=\(\sqrt{100}\)

= 10.

No es frecuente que tu resultado exacto esté de acuerdo con tu aproximación, así que nunca te preocupes si estás fuera por un poco.

Ejercicio

En los Ejercicios 1 - 8, indicar si el triple dado es o no un Triple pitagórico. Da una razón para tu respuesta.

Ejercicio\(\PageIndex{1}\)

(8, 15, 17)

Contestar

Sí, porque\(8^2 + 15^2 = 17^2\)

Ejercicio\(\PageIndex{2}\)

(7, 24, 25)

Ejercicio\(\PageIndex{3}\)

(8, 9, 17)

Contestar

No, porque\(8^2+9^2 \ne 17^2\)

Ejercicio\(\PageIndex{4}\)

(4, 9, 13)

Ejercicio\(\PageIndex{5}\)

(12, 35, 37)

Contestar

Sí, porque\(12^2 + 35^2 = 37^2\)

Ejercicio\(\PageIndex{6}\)

(12, 17, 29)

Ejercicio\(\PageIndex{7}\)

(11, 17, 28)

Contestar

No, porque\(11^2 + 17^2 \ne 28^2\)

Ejercicio\(\PageIndex{8}\)

(11, 60, 61)

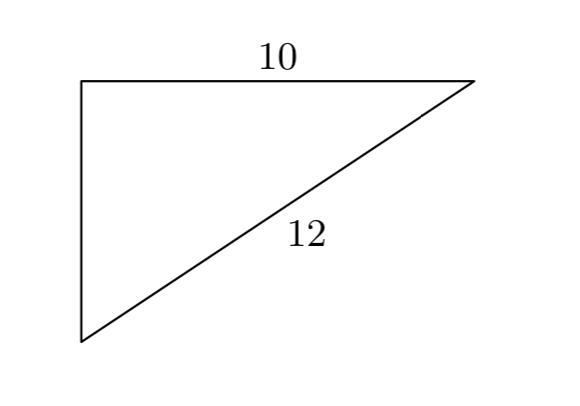
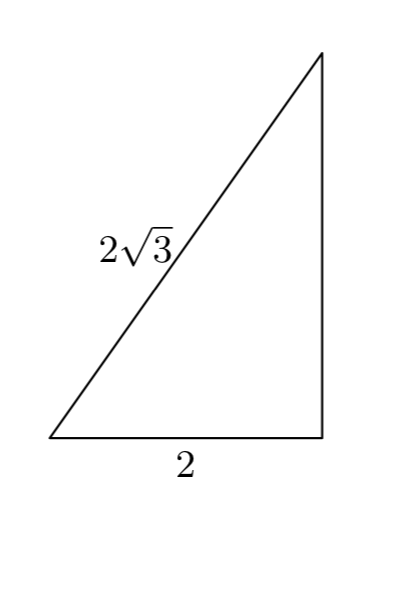
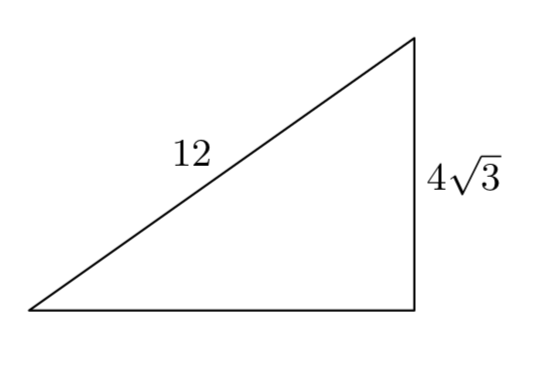
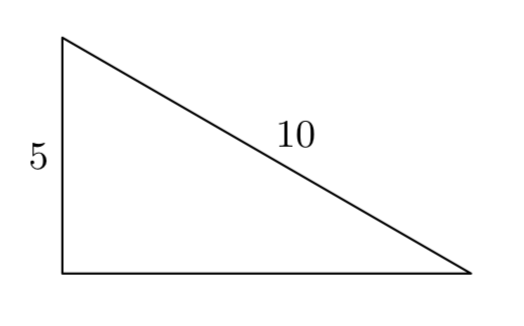
En los Ejercicios 9 - 16, establecer una ecuación para modelar las limitaciones del problema y resolver. Usa tu respuesta para encontrar el lado que falta del triángulo rectángulo dado. Incluye un boceto con tu solución y comprueba tu resultado.

Ejercicio\(\PageIndex{9}\)

Contestar

4

Ejercicio\(\PageIndex{10}\)

Ejercicio\(\PageIndex{11}\)

Contestar

\(4\sqrt{2}\)

Ejercicio\(\PageIndex{12}\)

Ejercicio\(\PageIndex{13}\)

Contestar

\(2\sqrt{2}\)

Ejercicio\(\PageIndex{14}\)

Ejercicio\(\PageIndex{15}\)

Contestar

\(5\sqrt{3}\)

Ejercicio\(\PageIndex{16}\)

En los Ejercicios 17 - 20, establecer una ecuación que modele las restricciones del problema. Resuelve la ecuación y usa el resultado para responder a la pregunta. Mira hacia atrás y comprueba tu resultado.

Ejercicio\(\PageIndex{17}\)

Las patas de un triángulo rectángulo son enteros positivos consecutivos. La hipotenusa tiene longitud 5. ¿Cuáles son las longitudes de las piernas?

Contestar

Las patas tienen longitudes 3 y 4.

Ejercicio\(\PageIndex{18}\)

Las patas de un triángulo rectángulo son números enteros pares consecutivos. La hipotenusa tiene longitud 10. ¿Cuáles son las longitudes de las piernas?

Ejercicio\(\PageIndex{19}\)

Una pata de un triángulo rectángulo es 1 centímetro menos del doble de la longitud del primer tramo. Si la longitud de la hipotenusa es de 17 centímetros, encuentra las longitudes de las piernas.

Contestar

Las patas tienen longitudes de 8 y 15 centímetros.

Ejercicio\(\PageIndex{20}\)

Una pierna de un triángulo rectángulo mide 3 pies más larga que 3 veces la longitud del primer tramo. La longitud de la hipotenusa es de 25 pies. Encuentra los largos de las piernas.

Ejercicio\(\PageIndex{21}\)

A Pitágoras se le acreditan las siguientes fórmulas que pueden ser utilizadas para generar Triples Pitágoras.

a = m

\(b = \frac{m^2−1}{2}\),

\(c = \frac{m^2+1}{2}\)

Utilice la técnica del Ejemplo 6 para demostrar que las fórmulas dadas anteriormente generarán Triples Pitágoras, siempre que m sea un entero impar positivo mayor que uno. En segundo lugar, generar al menos 3 instancias de Triples Pitágoras con la fórmula de Pitágoras.

Contestar

(3, 4, 5), (5, 12, 13) y (7, 24, 25), con m = 3, 5 y 7, respectivamente.

Ejercicio\(\PageIndex{22}\)

A Platón (380 a.C.) se le acreditan las siguientes fórmulas que pueden ser utilizadas para generar Triples pitagóricos.

\(a = 2m\)

\(b = m^2 − 1\),

\(c = m^2 + 1\)

Utilice la técnica del Ejemplo 6 para demostrar que las fórmulas dadas anteriormente generarán Triples Pitágoras, siempre que m sea un entero positivo mayor que 1. En segundo lugar, generar al menos 3 instancias de Triples Pitágoras con la fórmula de Platón.

En los Ejercicios 23 - 28, establecer una ecuación que modele las restricciones del problema. Resuelve la ecuación y usa el resultado para responder. Mira hacia atrás y comprueba tu respuesta.

Ejercicio\(\PageIndex{23}\)

Fritz y Greta están plantando un jardín rectangular de 12 pies por 18 pies, y lo están colocando usando una cuerda. A ellos les gustaría saber la longitud de una diagonal para asegurarse de que se forman ángulos rectos. Encuentra la longitud de una diagonal. Aproxime su respuesta a un radio de 0.1 pies.

Contestar

21. 63 pies

Ejercicio\(\PageIndex{24}\)

Angelina y Markos están plantando un jardín rectangular de 20 pies por 28 pies, y lo están colocando usando una cuerda. A ellos les gustaría saber la longitud de una diagonal para asegurarse de que se forman ángulos rectos. Encuentra la longitud de una diagonal. Aproxime su respuesta a un radio de 0.1 pies.

Ejercicio\(\PageIndex{25}\)

La base de un cable de sujeción de 36 pies de largo se encuentra a 16 pies de la base del poste telefónico que está anclando. ¿Qué tan alto llega el cable de tipo arriba del poste? Aproxime su respuesta dentro de 0.1.

Contestar

32. 25 pies

Ejercicio\(\PageIndex{26}\)

La base de un cable de sujeción de 35 pies de largo se encuentra a 10 pies de la base del poste telefónico que está anclando. ¿Qué tan alto llega el cable de sujeción al poste? Aproxime su respuesta a un radio de 0.1 pies.

Ejercicio\(\PageIndex{27}\)

Un receptor estéreo está en una esquina de una habitación rectangular de 13 pies por 16 pies. El cable del altavoz correrá debajo de una alfombra, en diagonal, a un altavoz en la esquina más alejada. Si se requieren 3 pies de holgura en cada extremo, ¿cuánto tiempo se debe comprar un trozo de alambre? Aproxime su respuesta a un radio de 0.1 pies.

Contestar

26. 62 pies

Ejercicio\(\PageIndex{28}\)

Un receptor estéreo está en una esquina de una habitación rectangular de 10 pies por 15 pies. El cable del altavoz correrá debajo de una alfombra, en diagonal, a un altavoz en la esquina más alejada. Si se requieren 4 pies de holgura en cada extremo, ¿cuánto tiempo se debe comprar un trozo de alambre? Aproxime su respuesta a un radio de 0.1 pies.

En los Ejercicios 29 - 38, usa la fórmula de distancia para encontrar la distancia exacta entre los puntos dados.

Ejercicio\(\PageIndex{29}\)

(−8, −9) y (6, −6)

Contestar

\(\sqrt{205}\)

Ejercicio\(\PageIndex{30}\)

(1, 0) y (− 9, − 2)

Ejercicio\(\PageIndex{31}\)

(− 9, 1) y (− 8, 7)

Contestar

\(\sqrt{37}\)

Ejercicio\(\PageIndex{32}\)

(0, 9) y (3, 1)

Ejercicio\(\PageIndex{33}\)

(6, −5) y (−9, −2)

Contestar

\(\sqrt{234} = 3\sqrt{26}\)

Ejercicio\(\PageIndex{34}\)

(−5, 6) y (1, 4)

Ejercicio\(\PageIndex{35}\)

(−7, 7) y (−3, 6)

Contestar

\(\sqrt{17}\)

Ejercicio\(\PageIndex{36}\)

(−7, −6) y (−2, −4)

Ejercicio\(\PageIndex{37}\)

(4, −3) y (−9, 6)

Contestar

\(\sqrt{250} = 5\sqrt{10}\)

Ejercicio\(\PageIndex{38}\)

(−7, −1) y (4, −5)

En los Ejercicios 39 - 42, establecer una ecuación que modele las restricciones del problema. Resuelve la ecuación y usa el resultado para responder a la pregunta. Mira hacia atrás y comprueba tu resultado.

Ejercicio\(\PageIndex{39}\)

Encuentra k para que el punto (4, k) esté a\(2\sqrt{2}\) unidades lejos del punto (2, 1).

Contestar

k = 3, −1.

Ejercicio\(\PageIndex{40}\)

Encuentra k así que el punto (k, 1) está a\(2\sqrt{2}\) unidades lejos del punto (0, −1)

Ejercicio\(\PageIndex{41}\)

Encuentra k así que el punto (k, 1) está a\(\sqrt{17}\) unidades lejos del punto (2, −3)

Contestar

k = 1, 3.

Ejercicio\(\PageIndex{42}\)

Encuentra k para que el punto (−1, k) esté a\(\sqrt{13}\) unidades lejos del punto (−4, −3).

Ejercicio\(\PageIndex{43}\)

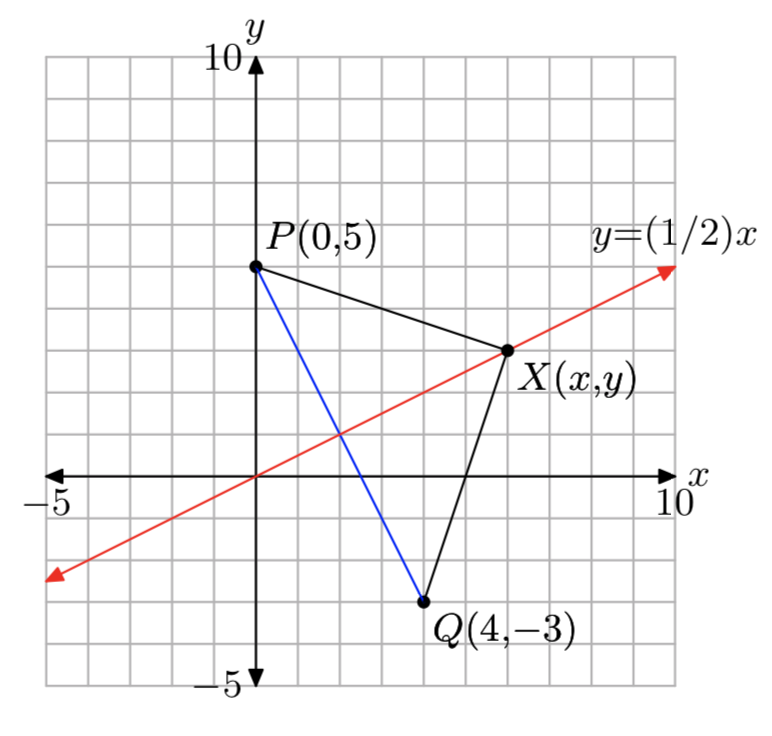
Configure un sistema de coordenadas en una hoja de papel cuadriculado. Etiquetar y escalar cada eje. Traza los puntos P (0, 5) y Q (4, −3) en tu sistema de coordenadas.

a) Trazar varios puntos que son equidistantes de los puntos P y Q en su sistema de coordenadas. ¿Qué gráfica obtienes si trazas todos los puntos que son equidistantes de los puntos P y Q? Determine la ecuación de la gráfica examinando la imagen resultante en su sistema de coordenadas.

b) Usa la fórmula de distancia para encontrar la ecuación de la gráfica de todos los puntos que son equidistantes de los puntos P y Q. Pista: Let (x, y) representar un punto arbitrario en la gráfica de todos los puntos equidistantes de los puntos P y Q. Calcular las distancias desde el punto (x, y) hasta los puntos P y Q por separado, luego establecerlos iguales y simplificar la ecuación resultante. Obsérvese que este enfoque analítico debe proporcionar una ecuación que coincida con la encontrada por el enfoque gráfico en la parte (a).

Contestar

a) En la figura que sigue, XP = XQ.

b)\(y = \frac{1}{2}x\)

Ejercicio\(\PageIndex{44}\)

Configure un sistema de coordenadas en una hoja de papel cuadriculado. Etiquetar y escalar cada eje. Trazar el punto P (0, 2) y etiquetarlo con sus coordenadas. Dibuja la línea y = −2 y etiquétela con su ecuación.

a) Trace varios puntos que son equidistantes del punto P y la línea y = −2 en su sistema de coordenadas. Qué gráfica obtienes si trazas todos los puntos que son equidistantes de los puntos P y la línea y = −2.

b) Usa la fórmula de distancia para encontrar la ecuación de la gráfica de todos los puntos que son equidistantes de los puntos P y la línea y = −2. Sugerencia: Let (x, y) representar un punto arbitrario en la gráfica de todos los puntos equidistantes de los puntos P y la línea y = −2. Calcule las distancias desde el punto (x, y) hasta los puntos P y la línea y = −2 por separado, luego configúrelas iguales y simplifique la ecuación resultante.

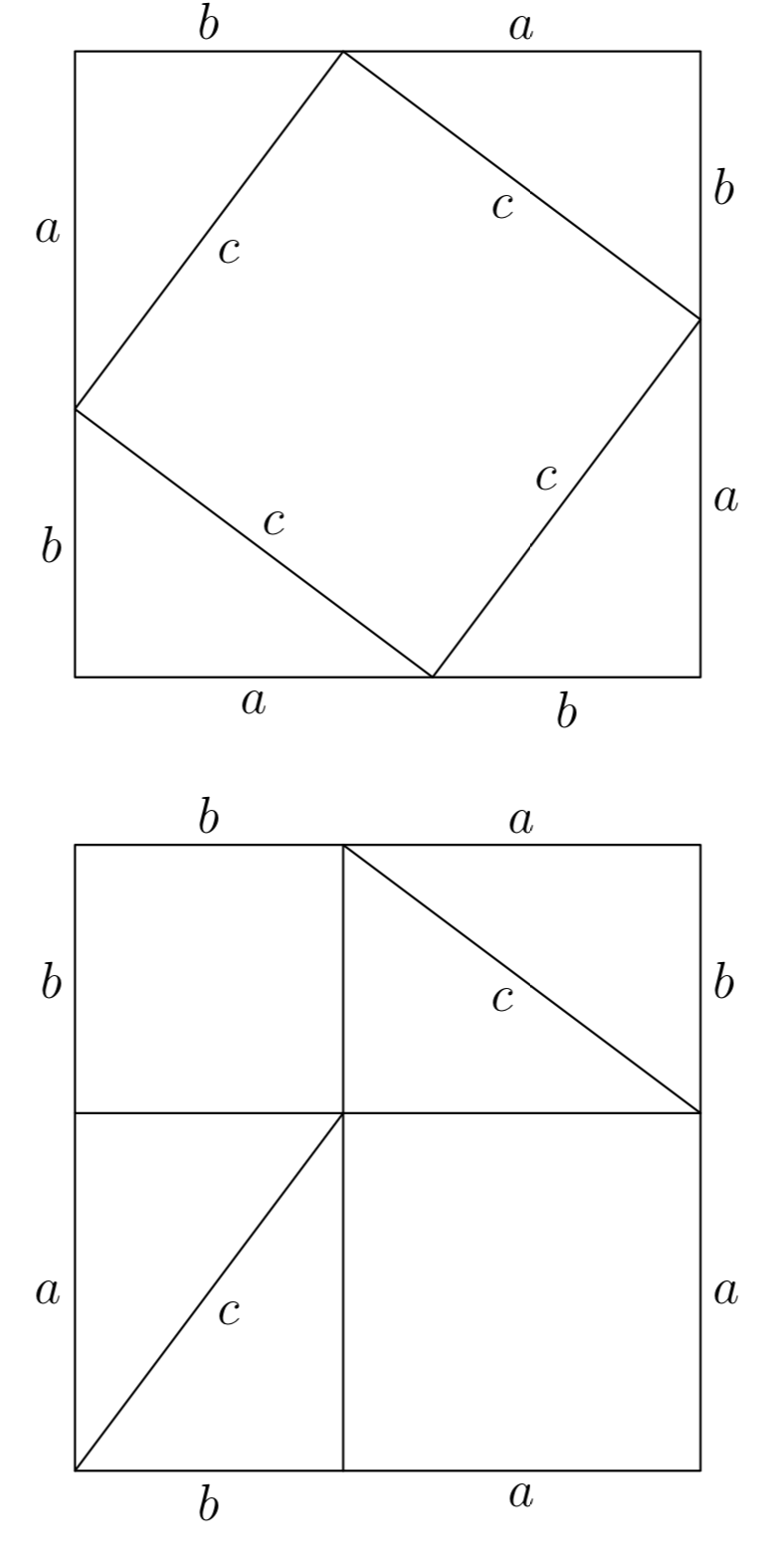
Ejercicio\(\PageIndex{45}\)

Copia la siguiente figura en una hoja de papel cuadriculado. Cortar las piezas de la primera figura con unas tijeras, luego reorganizarlas para formar la segunda figura. Explique cómo esto prueba el Teorema de Pitágoras.

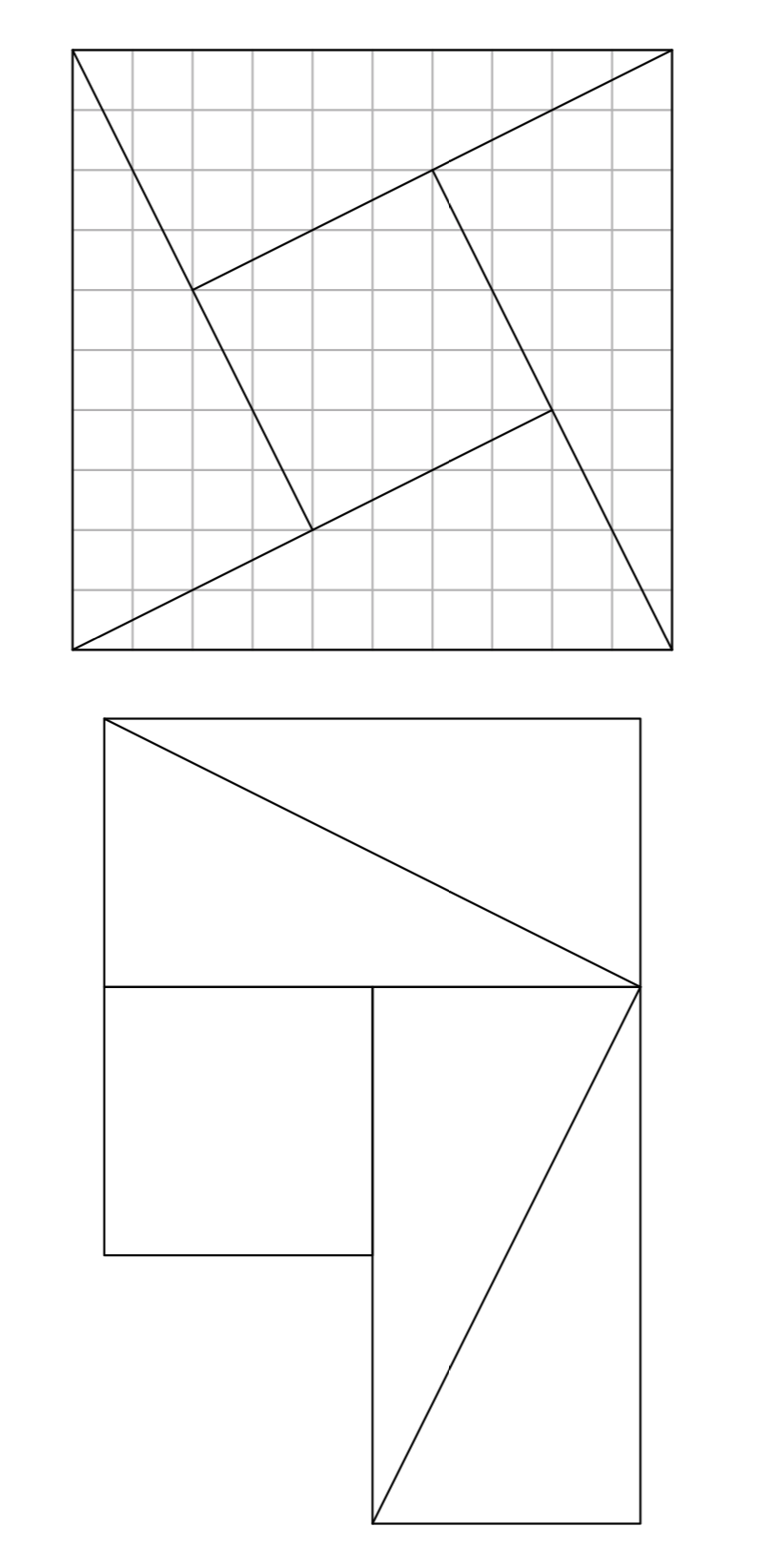
Ejercicio\(\PageIndex{46}\)

Compara esta imagen con la que sigue y explica cómo esto prueba el Teorema de Pitágoras.

​​​​​​​