9.5: Ecuaciones radicales
- Page ID
- 110677
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Ecuaciones radicales
En esta sección vamos a resolver ecuaciones que contienen una o más expresiones radicales. En el caso de que podamos aislar la expresión radical en un lado de la ecuación, simplemente podemos elevar ambos lados de la ecuación a un poder que eliminará la expresión radical. Por ejemplo, si
\(\sqrt{x−1} = 2\)(1)
entonces podemos cuadrar ambos lados de la ecuación, eliminando el radical.
\(\sqrt{x−1}^2 = (2)^2\)
x−1=4
Ahora que se elimina el radical, podemos apelar a técnicas bien entendidas para resolver la ecuación que queda. En este caso, solo necesitamos sumar 1 a ambos lados de la ecuación para obtener
x = 5.
Esta solución se comprueba fácilmente. Sustituir x = 5 en la ecuación original (1).
\(\sqrt{x−1} = 2\)
\(\sqrt{5−1} = 2\)
\(\sqrt{4} = 2\)
La última línea es válida porque la “raíz cuadrada positiva de 4” es efectivamente 2.
Esto parece bastante sencillo, pero hay algunas sutilezas. Veamos otro ejemplo, uno con una ecuación bastante similar a la ecuación.
Ejemplo\(\PageIndex{2}\)
Resuelve la ecuación\(\sqrt{x−1} = −2\) para x.
Si estudias cuidadosamente la ecuación
\(\sqrt{x−1} = −2\)(3)
podrías detectar de inmediato una dificultad. El lado izquierdo de la ecuación requiere una “raíz cuadrada positiva”, pero el lado derecho de la ecuación es negativo. Intuitivamente, no puede haber soluciones.
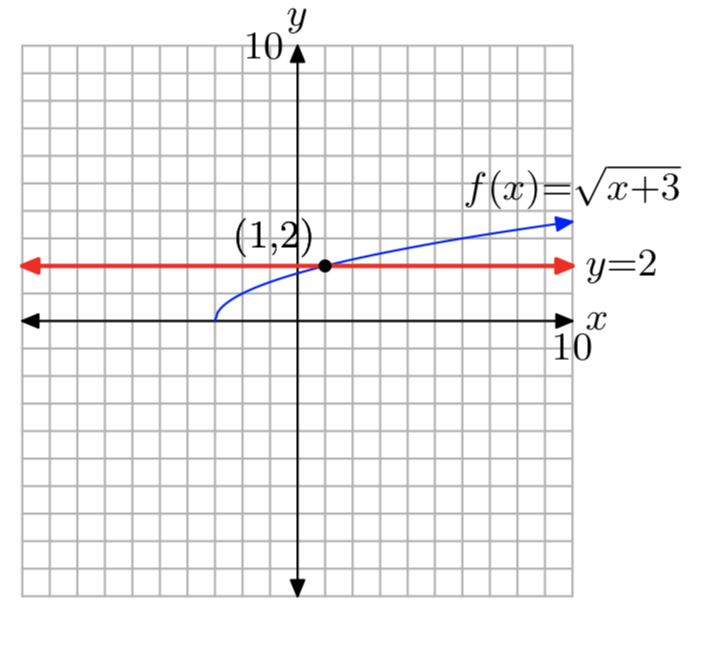
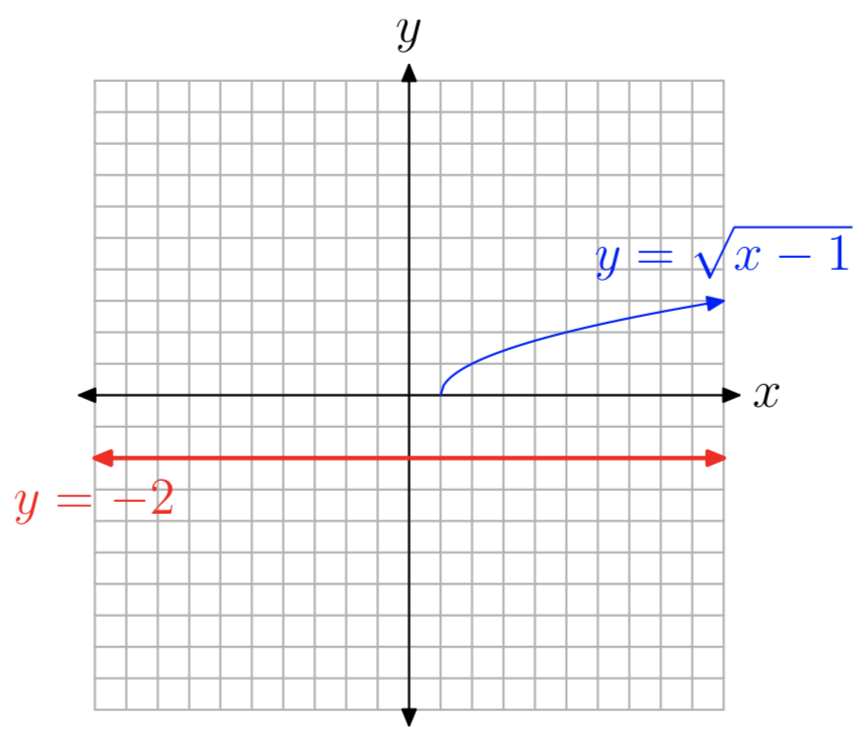
Una mirada a las gráficas de cada lado de la ecuación también revela el problema. Las gráficas de\(y = \sqrt{x−1}\) e y = −2 se muestran en la Figura 1. Tenga en cuenta que las gráficas no se cruzan, por lo que la ecuación no\(\sqrt{x−1} = −2\) tiene solución.
Sin embargo, observe lo que sucede cuando cuadramos ambos lados de la ecuación (3).
\((\sqrt{x − 1})^2 = (−2)^2\)
\(x−1=4\)(4)
Este resultado es idéntico al resultado que obtuvimos cuando cuadramos ambos lados de la ecuación\(\sqrt{x−1} = 2\) anterior. Si continuamos, sumando 1 a ambos lados de la ecuación, obtenemos
x = 5.
Pero esto no puede ser correcto, ya que tanto la intuición como las gráficas de la Figura 1 han demostrado que la ecuación no\(\sqrt{x−1} = −2\) tiene solución.
Comprobemos la solución x= 5 en la ecuación original.
\(\sqrt{x−1} = −2\)
\(\sqrt{5−1} = −2\)
\(\sqrt{4} = −2\)
Debido a que la “raíz cuadrada positiva de 4” no es igual a − 2, esta última línea es incorrecta y la solución x = 5 no comprueba la ecuación\(\sqrt{x−1} = −2\). Debido a que la única solución que encontramos no comprueba, la ecuación no tiene soluciones.
La discusión en el Ejemplo 2 dicta cautela.
ADVERTENCIA\(\PageIndex{5}\)
Siempre que cuadras ambos lados de una ecuación, existe la posibilidad de que puedas introducir soluciones extrañas, soluciones “extra” que no registrarán el problema original.
Sólo hay una manera de evitar este dilema de ecuaciones extrañas.
RESOLUCIONES DE
Siempre que cuadres ambos lados de una ecuación, debes verificar cada una de tus soluciones en la ecuación original. Esta es la única manera de estar seguro de que tiene una solución válida.
Cuadrando un Binomio
Como hemos visto una y otra vez, la cuadratura de un patrón binomial es de suma importancia.
ESCUADRADO DE UN BINOMIAL
Si a y b son números reales, entonces
\((a+b)^2 = a^2+2ab+b^2\).
La cuadratura de un patrón binomial jugará un papel importante en el resto de los ejemplos de esta sección.
Veamos algunos ejemplos de su uso.
Ejemplo\(\PageIndex{6}\)
Expandir y simplificar\((1+\sqrt{x})^2\) mediante el uso de la cuadratura de un patrón binomial. Asumir eso\(x \ge 0\).
El supuesto que\(x \ge 0\) se requiere, de lo contrario la expresión\(\sqrt{x}\) involucra la raíz cuadrada de un número negativo, que no es un número real.
La cuadratura de un patrón binomial nos dice cuadrar el primer y segundo términos. No obstante, también hay un término medio, que se encuentra tomando el producto del primer y segundo término, multiplicando posteriormente el resultado por 2.
\((1 + \sqrt{x})^2 = (1)^2 + 2(1)(\sqrt{x}) + (\sqrt{x})^2\)
=\(1+2\sqrt{x}+x\)
Veamos otro ejemplo.
Ejemplo\(\PageIndex{7}\)
Expandir y simplificar\((\sqrt{x+1}−\sqrt{x})^2\) mediante el uso de la cuadratura de un patrón binomial. Comenta sobre el dominio de esta expresión.
Para que esta expresión tenga sentido, debemos evitar tomar la raíz cuadrada de un número negativo. De ahí que ambas expresiones bajo las raíces cuadradas deben ser no negativas (positivas o cero). Es decir,
\[\begin{array}{ccc} {x+1 \ge 0}&{\text{and}}&{x \ge 0}\\ \nonumber \end{array}\]
Resolviendo cada una de estas desigualdades de forma independiente, obtenemos el hecho de que
\[\begin{array}{ccc} {x \ge −1}&{\text{and}}&{x \ge 0}\\ \nonumber \end{array}\]
Por la palabra “y”, el dominio solicitado es el conjunto de todos los números que satisfacen ambas desigualdades, es decir, el conjunto de todos los números reales que son mayores o iguales a cero. Es decir, el dominio de la expresión es\({x : x ≥ 0}\).
Ahora ampliaremos la expresión\((\sqrt{x+1}−\sqrt{x})^2\) usando la cuadratura de un patrón binomial.
\((\sqrt{x+1}−\sqrt{x})^2 = (\sqrt{x+1})^2−2(\sqrt{x+1})(\sqrt{x})+(\sqrt{x})^2\)
=\(x+1+2\sqrt{(x+1)x}+x\)
=\(2x+1+2\sqrt{x^2 +x}\)
Aislar el Radical
Nuestro mantra será la frase estratégica “Aislar al radical”.
Aislar el radical
Cuando resuelva ecuaciones que contienen un radical, aísle el radical por sí mismo en un lado de la ecuación.
Aunque esto no siempre es posible (algunas ecuaciones podrían contener más de una expresión radical), es posible en nuestro siguiente ejemplo.
Ejemplo\(\PageIndex{8}\)
Resolver la ecuación
\(1+\sqrt{4x+13} = 2x\) para x (9)
Veamos una solución de calculadora gráfica. Hemos cargado los lados izquierdo y derecho de\(1+\sqrt{4x+13} = 2x\) en Y1 e Y2, respectivamente, como se muestra en la Figura 2 (a). Luego usamos 6: ZStandard y la utilidad de intersección en el menú CALC para determinar las coordenadas del punto de intersección de\(y = 1+\sqrt{4x+13}\) y = 2x, como se muestra en la Figura 2 (b).
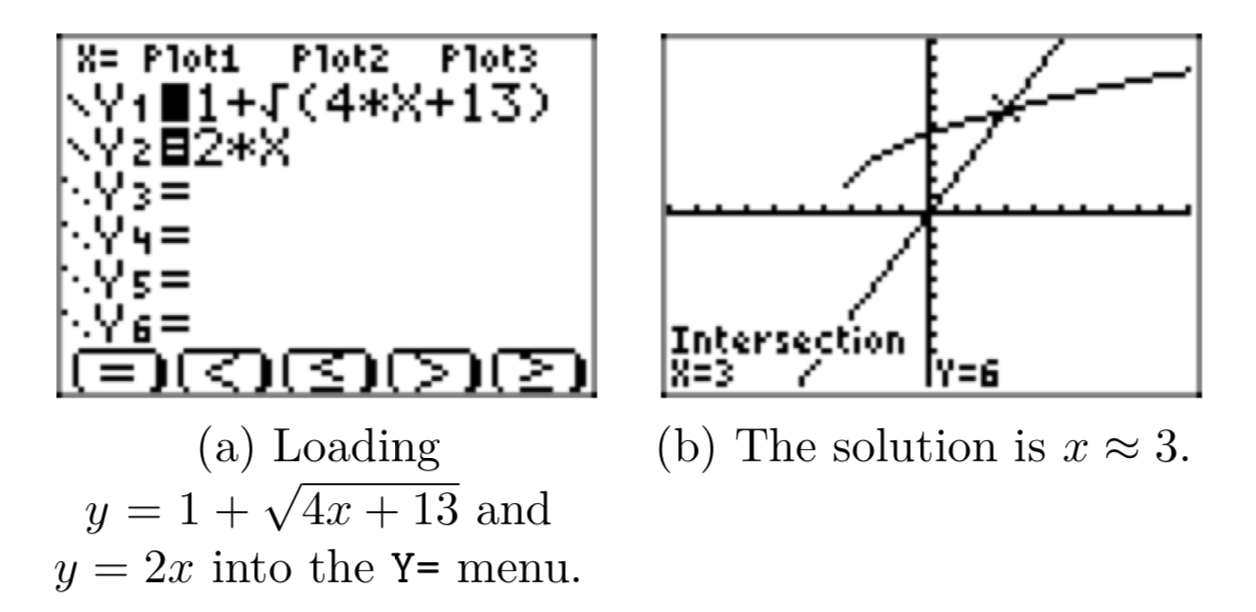
Ahora vamos a presentar una solución algebraica, pero tenga en cuenta que estamos prevenidos de que sólo hay una solución y creemos que la solución es\(x \approx 3\). Por supuesto, esto es solo una aproximación, como siempre es el caso cuando recogemos nuestra calculadora (nuestra máquina de aproximación).
Canta la frase de estrategia “aísle al radical”, luego aísle el radical en un lado de la ecuación. Lograremos esta directiva restando 1 de ambos lados de la ecuación.
\(1+\sqrt{4x+13} = 2x\)
\(\sqrt{4x+13} = 2x−1\)
A continuación, cuadrar ambos lados de la ecuación.
\((\sqrt{4x + 13})^2 = (2x−1)^2\)
La cuadratura elimina el radical de la izquierda, pero debemos usar la cuadratura de un patrón binomial para cuadrar el binomio en el lado derecho de la ecuación.
\(4x+13 = (2x)^2−2(2x)(1)+(1)^2\)
\(4x+13 = 4x^2−4x+1\)
Hemos logrado eliminar todas las raíces cuadradas de la ecuación con nuestra estrategia de “aislar lo radical”. La ecuación que queda es no lineal (hay una potencia de x mayor que 1), por lo que queremos hacer que un lado de la ecuación sea igual a cero. Esto lo haremos restando 4x y 13 de ambos lados de la ecuación.
\(0 = 4x^2−4x+1−4x−13\)
\(0 = 4x^2−8x−12\)
En este punto, tenga en cuenta que cada término del lado derecho de la ecuación es divisible por 4. Divide ambos lados de la ecuación por 4, luego usa la prueba ac para factorial el resultado.
\(0 = x^2−2x−3\)
0 = (x−3) (x+1)
Establece cada factor en el lado derecho de esta última ecuación para obtener las soluciones x = 3 y x = −1.
Obsérvese que x = 3 coincide con la solución encontrada al graficar en la Figura 2 (b). Sin embargo, ha aparecido una solución “extra” x = −1. Recuerde que cuadramos ambos lados de la ecuación original, por lo que es posible que se hayan introducido soluciones extrañas. Necesitamos verificar cada una de nuestras soluciones sustituyéndolas en la ecuación original (9).
Nuestra gráfica en la Figura 2 (b) agrega crédito a la solución analítica x = 3, así que verifiquemos primero esa. Sustituir x = 3 en la ecuación original.
\(1+\sqrt{4x+13} = 2x\)
\(1+\sqrt{4(3)+13} = 2(3)\)
\(1+ \sqrt{25} = 6\)
\(1+5 = 6\)
Claramente, x = 3 comprueba y es una solución válida.
A continuación, comprobemos la solución “sospechosa” x = − 1 sustituyéndola en la ecuación original.
\(1+\sqrt{4x+13} = 2x\)
\(1 + \sqrt{4(−1) + 13} = 2(−1)\)
\(1+\sqrt{9} = −2\)
\(1+3 = −2\)
Claramente, x = −1 no comprueba y no es una solución.
Así, la única solución de\(1+\sqrt{4x+13} = 2x\) es x = 3. Los lectores deben tomar nota de cómo esa solución gráfica y la solución analítica se complementan entre sí.
Antes de mirar otro ejemplo, veamos uno de los errores más comunes cometidos en la solución algebraica de la ecuación.
Un error algebraico común
En esta sección discutimos uno de los errores algebraicos más comunes que se encuentran al resolver ecuaciones que contienen expresiones radicales.
ADVERTENCIA\(\PageIndex{10}\)
Muchos de los cálculos de esta sección son incorrectos. Son ejemplos de errores comunes de álgebra que se cometen al resolver ecuaciones que contienen radicales. Ten esto en cuenta y lee muy atentamente el material de esta sección.
Cuando se presenta con la ecuación
\(1+\sqrt{4x+13} = 2x\), (11)
algunos cuadrarán ambos lados de la ecuación de la siguiente manera.
\((1)^2 + (\sqrt{4x+13})^2 = (2x)^2\). (12)
llegando a
\(1+4x+13 = 4x^2\).
Haga un lado cero, luego divida ambos lados de la ecuación resultante por 2.
\(0=4x^2 −4x−14\)
\(0=2x^2 −2x−7\)
El lector cuidadoso ya se dará cuenta de que hemos recorrido el camino equivocado, ya que este resultado es bastante diferente al de un punto similar en la solución del Ejemplo 8. Sin embargo, podemos continuar con la solución usando la fórmula cuadrática para resolver la última ecuación para x Cuando comparamos\(2x^2−2x−7\) con\(ax^2+bx+c\), tenga en cuenta que a = 2, b=−2 y c=−7. Por lo tanto,
\(x = \frac{−b \pm \sqrt{b^2−4ac}}{2a}\)
=\(\frac{−(−2) \pm \sqrt{(−2)^2−4(2)(−7)}}{2(2)}\)
=\(\frac{2 \pm \sqrt{60}}{4}\)
Sin embargo, ninguna de estas “soluciones” representa la solución correcta que se encuentra en el Ejemplo 8, a saber, x = 3. Entonces, ¿qué hemos hecho mal?
El error ocurrió en el primer paso cuando cuadramos ambos lados de la ecuación (11). En efecto, para obtener la ecuación (12), en realidad no cuadramos ambos lados de la ecuación (11). Más bien, cuadramos cada uno de los términos individuales a cada lado de la ecuación.
Esto es un grave error. En esencia, comenzamos con una ecuación que tenía la forma
a + b = c, (13)
luego cuadró “ambos lados” de la siguiente manera.
\(a^2 + b^2 = c^2\). (14)
Esto no es válido. Por ejemplo, comience con
2 + 3 = 5
una ecuación completamente válida ya que la suma de 2 y 3 es 5. Ahora “cuadrado” como hicimos en la ecuación (14) para obtener
\(2^2 + 3^2 = 5^2\).
Sin embargo, tenga en cuenta que esto simplifica como
4+9 = 25,
así que ya no tenemos una ecuación válida.
El error cometido aquí es que cuadramos cada uno de los términos individuales en cada lado de la ecuación en lugar de cuadrar “cada lado” de la ecuación. Si hubiéramos hecho eso, habríamos estado bien, como se ve en este cálculo.
2+3=5
\((2+3)^2 =5^2\)
\(2^2 +2(2)(3)+3^2 =5^2\)
4+12+9 = 25
Solo recuerda, a+b = c no implica\(a^2+b^2 = c^2\).
ADVERTENCIA\(\PageIndex{15}\)
Ahora volveremos a corregir los cómputos.
Más de un radical
Veamos una ecuación que contiene más de un radical.
Ejemplo\(\PageIndex{16}\)
Resolver la ecuación
\(\sqrt{2x}+\sqrt{2x+3} = 3\)(17)
para x.
Comenzaremos con una solución gráfica de la ecuación. Primero, cargue las ecuaciones\(y = \sqrt{2x}+\sqrt{2x+3}\) e y = 3 en el menú Y =, como se muestra en la Figura 3 (a).
No podemos tomar la raíz cuadrada de un número negativo, por lo que cuando consideramos la función definida por la ecuación\(y = \sqrt{2x}+\sqrt{2x+3}\), ambas expresiones bajo los radicales deben ser no negativas. Es decir,
\[\begin{array}{ccc} {2x \ge 0}&{\text{and}}&{2x+3 \ge 0}\\ \nonumber \end{array}\]
Resolviendo cada uno de ellos independientemente,
\[\begin{array}{ccc} {x \ge 0}&{\text{and}}&{x \ge −\frac{3}{2}}\\ \nonumber \end{array}\]
Los números que son mayores o iguales a cero y mayores o iguales a\(−\frac{3}{2}\) son los números mayores o iguales a cero. De ahí que el dominio de la función definida por la ecuación\(y = \sqrt{2x}+\sqrt{2x+3}\), sea {x:\(x \ge 0\)}. Por lo tanto, no debería llegar como un shock cuando la gráfica de\(y = \sqrt{2x}+\sqrt{2x+3}\) se encuentra enteramente a la derecha de cero, como se muestra en la Figura 3 (b).
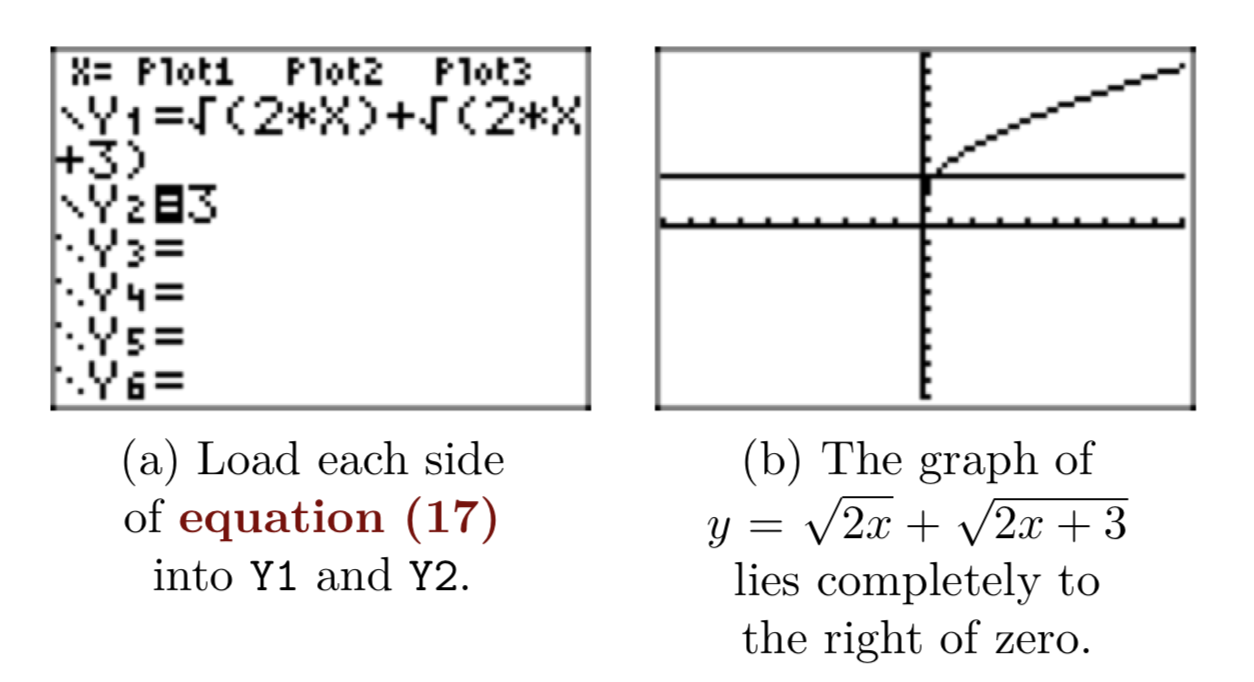
Es un poco difícil ver el punto de intersección en la Figura 3 (b), así que ajustemos los ajustes de VENTANA como se muestra en la Figura 4 (a). Como puede ver la Figura 4 (b), ésta resalta un poco más claramente el punto de intersección y la utilidad 5:intersectar en el menú CALC encuentra el punto de intersección mostrado en la Figura 4 (b).
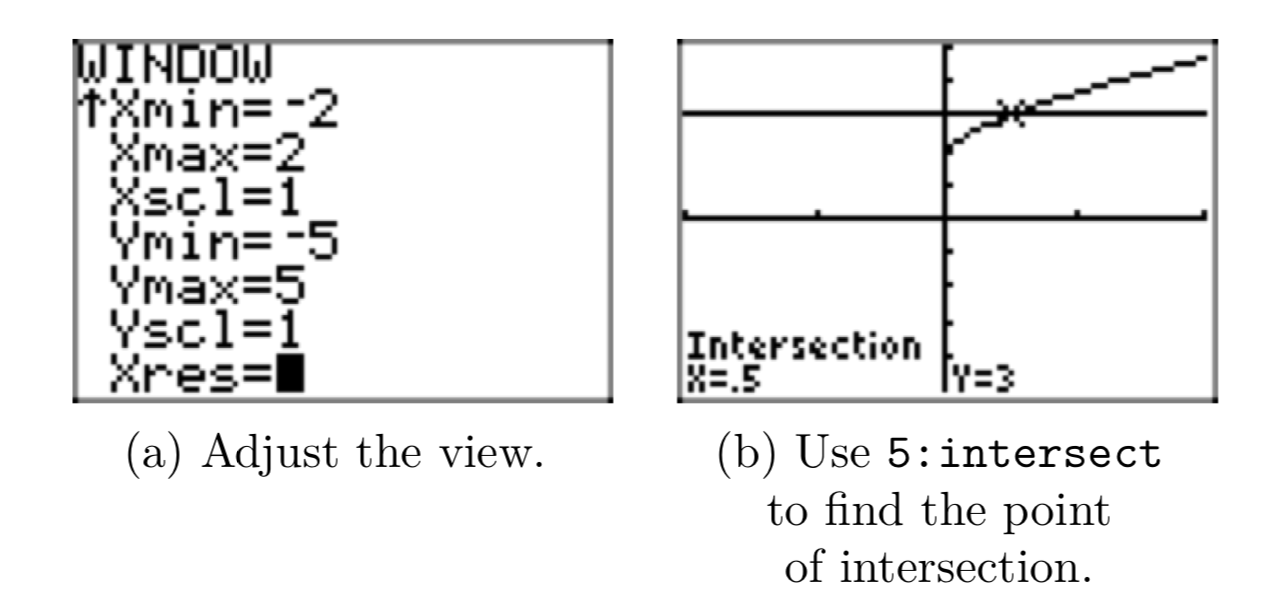
La calculadora gráfica reporta una solución (solo hay un punto de intersección), y el valor x del punto de intersección es aproximadamente\(x \approx 0.5\).
Ahora, veamos una solución algebraica. Dado que son dos expresiones radicales en esta ecuación, aislaremos una de ellas en un lado de la ecuación. Elegimos aislar la más compleja de las dos expresiones radicales en el lado izquierdo de la ecuación, luego cuadrar ambos lados de la ecuación resultante.
\(\sqrt{2x}+\sqrt{2x+3} = 3\)
\(\sqrt{2x+3} = 3−\sqrt{2x}\)
\((\sqrt{2x+3})^2 = (3−\sqrt{2x})^2\)
A la izquierda, la cuadratura elimina al radical. Para cuadrar el binomio de la derecha, utilizamos la cuadratura de un patrón binomial para obtener
\(2x+3 = (3)^2−2(3)(\sqrt{2x})+(\sqrt{2x})^2\)
\(2x+3 = 9−6\sqrt{2x}+2x\).
Todavía nos queda una expresión radical en el lado derecho de esta ecuación, así que seguiremos el mantra “aislar al radical”. Primero, resta 2x de ambos lados de la ecuación para obtener
\(3=9−6\sqrt{2x}\),
luego restar 9 de ambos lados de la ecuación.
\(−6=−6\sqrt{2x}\),
Hemos logrado aislar el término radical en un lado de la ecuación. Ahora, divida ambos lados de la ecuación por −6, luego cuadre ambos lados de la ecuación resultante.
\(1 = \sqrt{2x}\)
\((1)^2 = (\sqrt{2x})^2\)
\(1 = 2x\)
Divide ambos lados del último resultado por 2.
\(x = \frac{1}{2}\)
Tenga en cuenta que esto concuerda muy bien con nuestra solución gráfica (\(x \approx 0.5\)), pero verifiquemos nuestra solución\(x = \frac{1}{2}\) sustituyéndola en la ecuación original.
\(\sqrt{2x}+\sqrt{2x+3} = 3\)
\(\sqrt{2(\frac{1}{2})}+\sqrt{2(\frac{1}{2})+3} = 3\)
\(\sqrt{1}+\sqrt{4} = 3\)
1+2 = 3
Esta última afirmación es cierta, por lo que la solución\(x = \frac{1}{2}\) comprueba.
Ejercicio
Para las funciones racionales en los Ejercicios 1 - 6, realizar cada una de las siguientes tareas.
- Carga la función f y la línea y = k en tu calculadora gráfica. Ajuste la ventana de visualización para que todos los puntos de intersección de las dos gráficas sean visibles en su ventana de visualización.
- Copia la imagen en tu ventana de visualización en tu papel de tarea. Etiquetar y escalar cada eje con xmin, xmax, ymin e ymax. Etiquetar las gráficas con sus ecuaciones. Recuerda dibujar todas las líneas con una regla.
- Utilice la utilidad Intersect para determinar las coordenadas del punto (s) de intersección. Traza el punto de intersección en tu papel de tarea y etiquétalo con sus coordenadas.
- Resuelve la ecuación f (x) = k algebraicamente. Coloca tu trabajo y solución junto a tu gráfica. ¿Están de acuerdo las soluciones?
Ejercicio\(\PageIndex{2}\)
\(f(x) = \sqrt{4−x}\), k = 3
Ejercicio\(\PageIndex{4}\)
\(f(x) = \sqrt{3x+5}\), k = 5
Ejercicio\(\PageIndex{6}\)
\(f(x) = \sqrt{4−x}\), k = 5
En los Ejercicios 7 - 12, utilizar una técnica algebraica para resolver la ecuación dada. Consulta tus soluciones.
Ejercicio\(\PageIndex{7}\)
\(\sqrt{−5x+5} = 2\)
- Responder
-
\(\frac{1}{5}\)
Ejercicio\(\PageIndex{8}\)
\(\sqrt{4x+6} = 7\)
Ejercicio\(\PageIndex{9}\)
\(\sqrt{6x−8} = 8\)
- Responder
-
12
Ejercicio\(\PageIndex{10}\)
\(\sqrt{2x+4} = 2\)
Ejercicio\(\PageIndex{11}\)
\(\sqrt{−3x+1} = 3\)
- Responder
-
\(x = −\frac{8}{3}\)
Ejercicio\(\PageIndex{12}\)
\(\sqrt{4x+7} = 3\)
Para las funciones racionales en los Ejercicios 13-16 realizar cada una de las siguientes tareas.
- Carga la función f y la línea y = k en tu calculadora gráfica. Ajuste la ventana de visualización para que todos los puntos de intersección de las dos gráficas sean visibles en su ventana de visualización.
- Copia la imagen en tu ventana de visualización en tu papel de tarea. Etiquetar y escalar cada eje con xmin, xmax, ymin e ymax. Etiquetar las gráficas con sus ecuaciones. Recuerda dibujar todas las líneas con una regla.
- Utilice la utilidad Intersect para determinar las coordenadas del punto (s) de intersección. Traza el punto de intersección en tu papel de tarea y etiquétalo con sus coordenadas.
- Resuelve la ecuación f (x) = k algebraicamente. Coloca tu trabajo y solución junto a tu gráfica. ¿Están de acuerdo las soluciones?
Ejercicio\(\PageIndex{14}\)
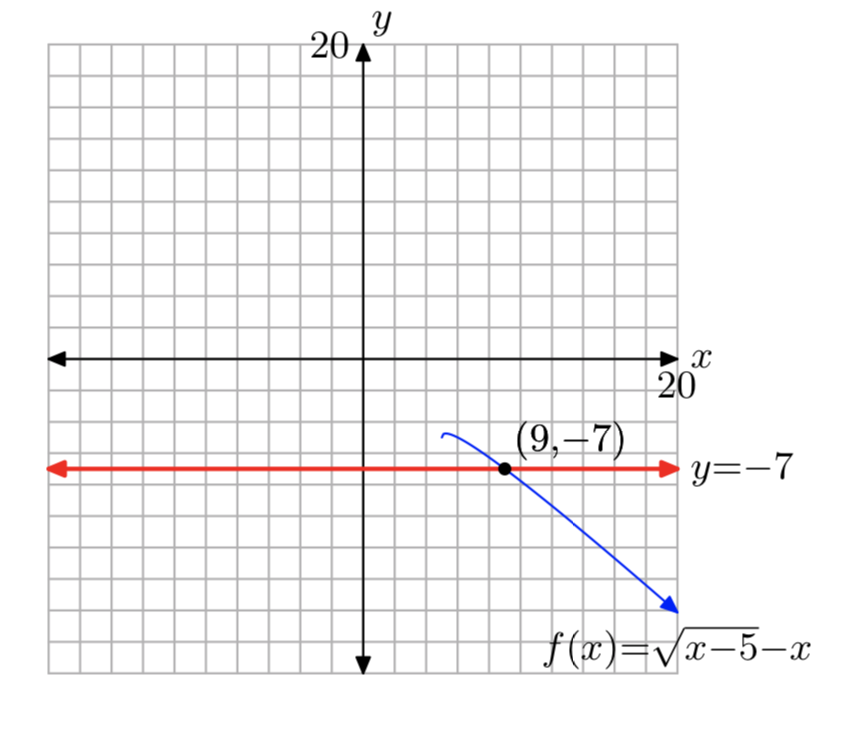
\(f(x) = \sqrt{x+6}−x\), k = 4
Ejercicio\(\PageIndex{16}\)
\(f(x) = \sqrt{x+5}+x\), k = 7
En Ejercicio17 - 24, utilizar una técnica algebraica para resolver la ecuación dada. Consulta tus soluciones.
Ejercicio\(\PageIndex{17}\)
\(\sqrt{x+1}+x = 5\)
- Responder
-
3
Ejercicio\(\PageIndex{18}\)
\(\sqrt{x+8}−x = 8\)
Ejercicio\(\PageIndex{19}\)
\(\sqrt{x+4}+x = 8\)
- Responder
-
5
Ejercicio\(\PageIndex{20}\)
\(\sqrt{x+8}−x = 2\)
Ejercicio\(\PageIndex{21}\)
\(\sqrt{x+5}−x = 3\)
- Responder
-
−1
Ejercicio\(\PageIndex{22}\)
\(\sqrt{x+5}+x = 7\)
Ejercicio\(\PageIndex{23}\)
\(\sqrt{x+9}−x = 9\)
- Responder
-
−8, −9
Ejercicio\(\PageIndex{24}\)
\(\sqrt{x+7}+x = 5\)
Para las funciones racionales en los Ejercicios 25 - 28, realizar cada una de las siguientes tareas.
- Carga la función f y la línea y =k en tu calculadora gráfica. Ajuste la ventana de visualización para que todos los puntos de intersección de las dos gráficas sean visibles en su ventana de visualización.
- Copia la imagen en tu ventana de visualización en tu papel de tarea. Etiquetar y escalar cada eje con xmin, xmax, ymin e ymax. Etiquetar las gráficas con sus ecuaciones. Recuerda dibujar todas las líneas con una regla.
- Utilice la utilidad Intersect para determinar las coordenadas del punto (s) de intersección. Traza el punto de intersección en tu papel de tarea y etiquétalo con sus coordenadas.
- Resuelve la ecuación f (x) = k algebraicamente. Coloca tu trabajo y solución junto a tu gráfica. ¿Están de acuerdo las soluciones?
Ejercicio\(\PageIndex{26}\)
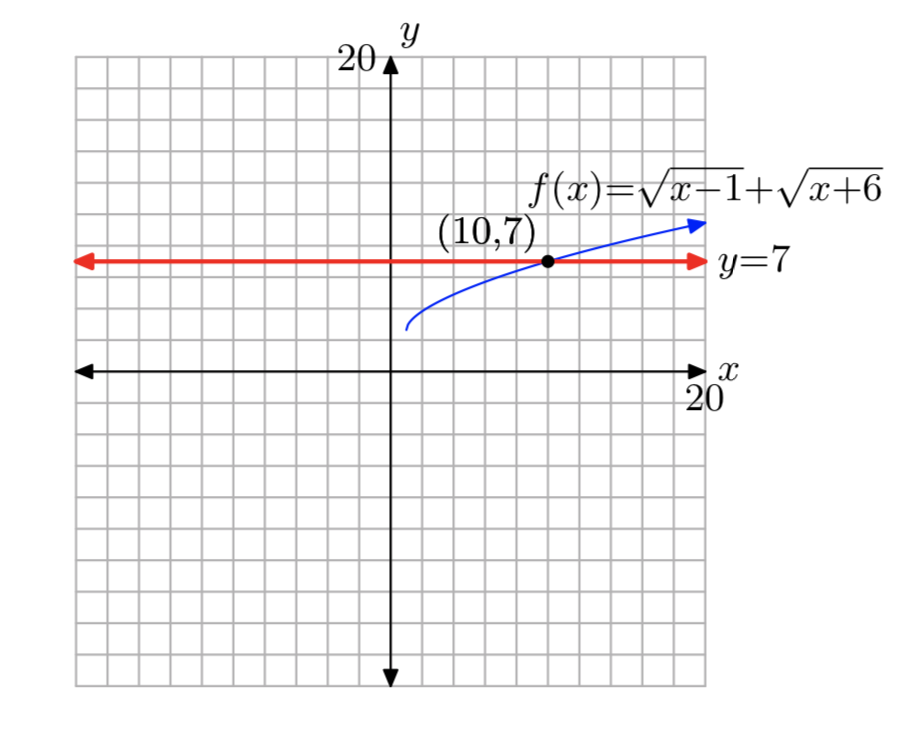
\(f(x) = \sqrt{x+2}+\sqrt{x+9}, k = 7\)
Ejercicio\(\PageIndex{28}\)
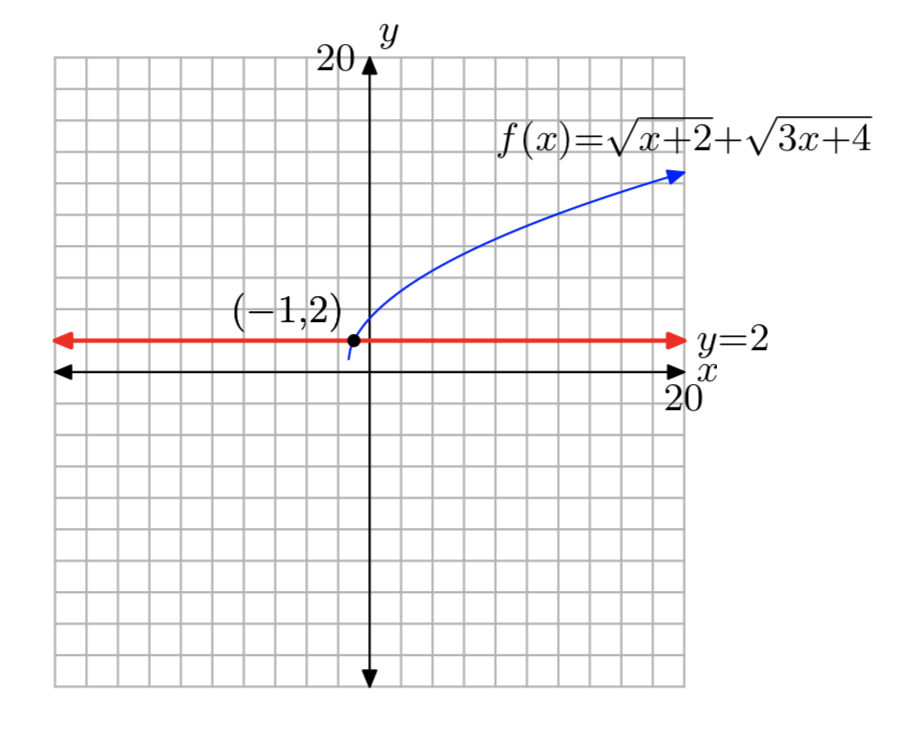
\(f(x)= \sqrt{6x+7}+\sqrt{3x+3}, k = 1\)
En los Ejercicios 29 - 40, utilizar una técnica algebraica para resolver la ecuación dada. Consulta tus soluciones.
Ejercicio\(\PageIndex{29}\)
\(\sqrt{x+46}−\sqrt{x−35} = 1\)
- Responder
-
1635
Ejercicio\(\PageIndex{30}\)
\(\sqrt{x−16}+\sqrt{x+16} = 8\)
Ejercicio\(\PageIndex{31}\)
\(\sqrt{x−19}+\sqrt{x−6} = 13\)
- Responder
-
55
Ejercicio\(\PageIndex{32}\)
\(\sqrt{x+31}−\sqrt{x+12} = 1\)
Ejercicio\(\PageIndex{33}\)
\(\sqrt{x−2}−\sqrt{x−49} = 1\)
- Responder
-
578
Ejercicio\(\PageIndex{34}\)
\(\sqrt{x+13}+\sqrt{x+8} = 5\)
Ejercicio\(\PageIndex{35}\)
\(\sqrt{x+27}−\sqrt{x−22} = 1\)
- Responder
-
598
Ejercicio\(\PageIndex{36}\)
\(\sqrt{x+10}+\sqrt{x+13} = 3\)
Ejercicio\(\PageIndex{37}\)
\(\sqrt{x+30}−\sqrt{x−38} = 2\)
- Responder
-
294
Ejercicio\(\PageIndex{38}\)
\(\sqrt{x+36}−\sqrt{x+11} = 1\)
Ejercicio\(\PageIndex{39}\)
\(\sqrt{x−17}+\sqrt{x+3} = 10\)
- Responder
-
33
Ejercicio\(\PageIndex{40}\)
\(\sqrt{x+18}+\sqrt{x+13} = 5\)