1.6E: Ejercicios

Última actualización
Guardar como PDF

Page ID: 112461

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

La práctica hace la perfección

Utilizar las propiedades conmutativas y asociativas

En los siguientes ejercicios, simplifique.

1. $43m+(−12n)+(−16m)+(−9n)$

Contestar: $27m+(−21n)$

2. $−22p+17q+(−35p)+(−27q)$

3. $\frac{3}{8}g+\frac{1}{12}h+\frac{7}{8}g+\frac{5}{12}h$

Contestar: $\frac{5}{4}g+\frac{1}{2}h$

4. $\frac{5}{6}a+\frac{3}{10}b+\frac{1}{6}a+\frac{9}{10}b$

5. $6.8p+9.14q+(−4.37p)+(−0.88q)$

Contestar: $2.43p+8.26q$

6. $9.6m+7.22n+(−2.19m)+(−0.65n)$

7. $−24·7·\frac{3}{8}$

Contestar: $−63$

8. $−36·11·\frac{4}{9}$

9. $\left(\frac{5}{6}+\frac{8}{15}\right)+\frac{7}{15}$

Contestar: $1\frac{5}{6}$

10. $\left(\frac{11}{12}+\frac{4}{9}\right)+\frac{5}{9}$

11. $17(0.25)(4)$

Contestar: $17$

12. $36(0.2)(5)$

13. $[2.48(12)](0.5)$

Contestar: $14.88$

14. $[9.731(4)](0.75)$

15. $12\left(\frac{5}{6}p\right)$

Contestar: $10p$

16. $20\left(\frac{3}{5}q\right)$

Utilizar las Propiedades de Identidad, Inversa y Cero

En los siguientes ejercicios, simplifique.

17. $19a+44−19a$

Contestar: $44$

18. $27c+16−27c$

19. $\frac{1}{2}+\frac{7}{8}+\left(−\frac{1}{2}\right)$

Contestar: $\frac{7}{8}$

20. $\frac{2}{5}+\frac{5}{12}+\left(−\frac{2}{5}\right)$

21. $10(0.1d)$

Contestar: $d$

22. $100(0.01p)$

23. $\frac{3}{20}·\frac{49}{11}·\frac{20}{3}$

Contestar: $\frac{49}{11}$

24. $\frac{13}{18}·\frac{25}{7}·\frac{18}{13}$

25. $\frac{0}{u−4.99}$, donde$u\neq 4.99$

Contestar: $0$

26. $0÷(y−\frac{1}{6})$, donde$x \neq 16$

27. $\frac{32−5a}{0}$, donde$32−5a\neq 0$

Contestar: undefined

28. $\frac{28−9b}{0}$, donde$28−9b\neq 0$

29. $\left(\frac{3}{4}+\frac{9}{10}m\right)÷0$, donde$\frac{3}{4}+\frac{9}{10}m\neq 0$

Contestar: undefined

30. $\left(\frac{5}{16}n−\frac{3}{7}\right)÷0$, donde$\frac{5}{16}n−\frac{3}{7}\neq 0$

Simplificar expresiones mediante la propiedad distributiva

En los siguientes ejercicios, simplifique el uso de la Propiedad Distributiva.

31. $8(4y+9)$

Contestar: $32y+72$

32. $9(3w+7)$

33. $6(c−13)$

Contestar: $6c−78$

34. $7(y−13)$

35. $\frac{1}{4}(3q+12)$

Contestar: $\frac{3}{4}q+3$

36. $\frac{1}{5}(4m+20)$

37. $9(\frac{5}{9}y−\frac{1}{3})$

Contestar: $5y−3$

38. $10(\frac{3}{10}x−\frac{2}{5})$

39. $12(\frac{1}{4}+\frac{2}{3}r)$

Contestar: $3+8r$

40. $12(\frac{1}{6}+\frac{3}{4}s)$

41. $15⋅\frac{3}{5}(4d+10)$

Responder: $36d+90$

42. $18⋅\frac{5}{6}(15h+24)$

43. $r(s−18)$

Responder: $rs−18r$

44. $u(v−10)$

45. $(y+4)p$

Responder: $yp+4p$

46. $(a+7)x$

47. $−7(4p+1)$

Responder: $−28p−7$

48. $−9(9a+4)$

49. $−3(x−6)$

Responder: $−3x+18$

50. $−4(q−7)$

51. $−(3x−7)$

Responder: $−3x+7$

52. $−(5p−4)$

53. $16−3(y+8)$

Responder: $−3y−8$

54. $18−4(x+2)$

55. $4−11(3c−2)$

Responder: $−33c+26$

56. $9−6(7n−5)$

57. $22−(a+3)$

Responder: $−a+19$

58. $8−(r−7)$

59. $(5m−3)−(m+7)$

Responder: $4m−10$

60. $(4y−1)−(y−2)$

61. $9(8x−3)−(−2)$

Responder: $72x−25$

62. $4(6x−1)−(−8)$

63. $5(2n+9)+12(n−3)$

Responder: $22n+9$

64. $9(5u+8)+2(u−6)$

65. $14(c−1)−8(c−6)$

Responder: $6c+34$

66. $11(n−7)−5(n−1)$

67. $6(7y+8)−(30y−15)$

Responder: $12y+63$

68. $7(3n+9)−(4n−13)$

Ejercicios de escritura

69. En sus propias palabras, declarar la Propiedad Asociativa de adición.

Responder: Las respuestas variarán.

70. Cuál es la diferencia entre la inversa aditiva y la inversa multiplicativa de un número

71. Simplifique el$8(x−\frac{1}{4})$ uso de la Propiedad Distributiva y explique cada paso.

Responder: Las respuestas variarán.

72. Explica cómo puedes multiplicar$4($5.97)$ sin papel o calculadora pensando en$$5.97$ como$6−0.03$ y luego usando la Propiedad Distributiva.

Autocomprobación

a. después de completar los ejercicios, utilice esta lista de verificación para evaluar su dominio de los objetivos de esta sección.

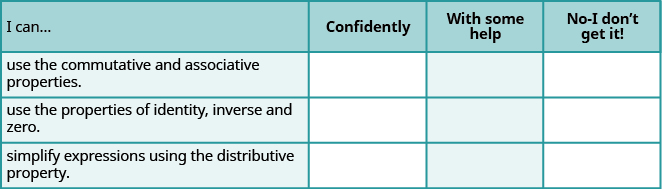
$Esta tabla tiene 4 columnas, 3 filas y una fila de cabecera. La fila de encabezado etiqueta cada columna puedo, con confianza, con algo de ayuda y no, no la consigo. La primera columna tiene las siguientes declaraciones: usar las propiedades conmutativas y asociativas, usar las propiedades de identidad, inversa y cero, simplificar expresiones usando la Propiedad Distributiva. Las columnas restantes están en blanco.$

b. Después de revisar esta lista de verificación, ¿qué harás para tener confianza en todos los objetivos?