Capítulo 1 Ejercicios de revisión

Última actualización
Guardar como PDF

Page ID: 112471

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

Ejercicios de revisión de capítulos

Usar el lenguaje del álgebra

Identificar múltiplos y factores

1. Utilice las pruebas de divisibilidad para determinar si 180 es divisible por 2, por 3, por 5, por 6 y por 10.

Responder: Divisible por$2,3,5,6$

2. Encuentra la factorización primo de 252.

3. Encuentra el múltiplo menos común de 24 y 40.

Responder: 120

En los siguientes ejercicios, simplifique cada expresión.

4. $24÷3+4(5−2)$

5. $7+3[6−4(5−4)]−3^2$

Responder: 4

Evaluar una expresión

En los siguientes ejercicios, evalúe las siguientes expresiones.

6. Cuando$x=4$, ⓐ $x^3$ ⓑ $5x$ ⓒ $2x^2−5x+3$

7. $2x^2−4xy−3y^2$cuándo$x=3$ y$y=1$

Responder: 3

Simplificar expresiones combinando términos similares

En los siguientes ejercicios, simplifique las siguientes expresiones combinando términos similares.

8. $12y+7+2y−5$

9. $14x^2−9x+11−8x^2+8x−6$

Responder: $6x^2−x+5$

Traducir una frase en inglés a una expresión algebraica

En los siguientes ejercicios, traduzca las frases en expresiones algebraicas.

10. ⓐ la suma de$4ab^2$ y$7a3b24ab^2$ y$7a^3b^2$

ⓑ el producto de$6y^2$ y$3y$

ⓓ$5y$ menos de$8y^2$

11. ⓐ once veces la diferencia de$y$ y dos

ⓑ la diferencia de once veces$y$ y dos

Responder: ⓐ$11(y−2)$
ⓑ$11y−2$

12. Dushko tiene monedas de cinco centavos y centavos en el bolsillo. El número de centavos es de cuatro menos de cinco el número de centavos. Que nn represente el número de monedas de cinco centavos. Escribe una expresión para el número de centavos.

Enteros

Simplificar expresiones con valor absoluto

En el siguiente ejercicio, rellene$<,>,$ o$=$ para cada uno de los siguientes pares de números.

13. ⓐ$−|7| \_\_\_−|−7|$

ⓑ$−8 \_\_\_−|−8|$

ⓒ$|−13| \_\_\_−13$

ⓓ$|−12| \_\_\_−(−12)$

Responder: ⓐ$=$
ⓑ$=$
ⓒ$>$
ⓓ$=$

En los siguientes ejercicios, simplifique.

14. $9−|3(4−8)|$

15. $12−3|1−4(4−2)|$

Responder: $−9$

Sumar y restar números enteros

En los siguientes ejercicios, simplifique cada expresión.

16. $−12+(−8)+7$

17. ⓐ$15−7$

ⓑ$−15−(−7)$

ⓒ$−15−7$

ⓓ$15−(−7)$

Responder: ⓐ$8$
ⓑ$−8$
ⓒ$−22$
ⓓ$22$

18. $−11−(−12)+5$

19. ⓐ$23−(−17)$ ⓑ$23+17$

Responder: ⓐ 40 ⓑ 40

20. $−(7−11)−(3−5)$

Multiplicar y dividir enteros

En el siguiente ejercicio, multiplique o divida.

21. ⓐ$−27÷9$ ⓑ$120÷(−8)$ ⓒ$4(−14)$ ⓓ$−1(−17)$

Responder: ⓐ$−3$ ⓑ$−15$ ⓒ$−56$ ⓓ$17$

Simplificar y evaluar expresiones con números enteros

En los siguientes ejercicios, simplifique cada expresión.

22. ⓐ$(−7)^3$ ⓑ$−7^3$

23. $(7−11)(6−13)$

Responder: 16

24. $63÷(−9)+(−36)÷(−4)$

25. $6−3|4(1−2)−(7−5)|$

Responder: $−12$

26. $(−2)^4−24÷(13−5)$

Para los siguientes ejercicios, evalúe cada expresión.

27. $(y+z)^2$cuándo$y=−4$ y$z=7$

Responder: 9

28. $3x^2−2xy+4y^2$cuándo$x=−2$ y$y=−3$

Traducir frases en inglés a expresiones algebraicas

En los siguientes ejercicios, traduzca a una expresión algebraica y simplifique si es posible.

29. la suma de$−4$ y$−9$, incrementada en$23$

Responder: $(−4+(−9))+23;10$

30. ⓐ la diferencia de 17 y −8 ⓑ resta 17 de −25

Usar números enteros en aplicaciones

En el siguiente ejercicio, resolver.

31. Temperatura El 10 de julio, la temperatura alta en Phoenix, Arizona, fue de 109°, y la alta en Juneau, Alaska, fue de 63°. ¿Cuál fue la diferencia entre la temperatura en Palm Springs y la temperatura en Whitefield?

Responder: $46°$

Fracciones

Simplificar fracciones

En los siguientes ejercicios, simplifique.

32. $\dfrac{204}{228}$

33. $−\dfrac{270x^3}{198y^2}$

Responder: $−\dfrac{15x^3}{11y^2}$

Multiplicar y dividir fracciones

En los siguientes ejercicios, realice la operación indicada.

34. $\left(−\dfrac{14}{15}\right)\left(\dfrac{10}{21}\right)$

35. $\dfrac{6x}{25}÷\dfrac{9y}{20}$

Responder: $\dfrac{8x}{15y}$

36. $\dfrac{−\frac{4}{9}}{\dfrac{8}{21}}$

Sumar y restar fracciones

En los siguientes ejercicios, realice la operación indicada.

37. $\dfrac{5}{18}+\dfrac{7}{12}$

Contestar: $\dfrac{31}{36}$

38. $\dfrac{11}{36}−\dfrac{15}{48}$

39. ⓐ$\dfrac{5}{8}+\dfrac{3}{4}$ ⓑ$\dfrac{5}{8}÷\dfrac{3}{4}$

Contestar: ⓐ$\dfrac{11}{8}$ ⓑ$\dfrac{5}{6}$

40. ⓐ$−\dfrac{3y}{10}−\dfrac{5}{6}$ ⓑ$−\dfrac{3y}{10}·\dfrac{5}{6}$

Utilizar el orden de operaciones para simplificar fracciones

En los siguientes ejercicios, simplifique.

41. $\dfrac{4·3−2·5}{−6·3+2·3}$

Contestar: $−\dfrac{1}{6}$

42. $\dfrac{4(7−3)−2(4−9)}{−3(4+2)+7(3−6)}$

43. $\dfrac{4^3−4^2}{(\dfrac{4}{5})^2}$

Contestar: 75

Evaluar expresiones variables con fracciones

En los siguientes ejercicios, evalúe.

44. $4x^2y^2$cuándo$x=\dfrac{2}{3}$ y$y=−\dfrac{3}{4}$

45. $\dfrac{a+b}{a−b}$cuándo$a=−4$ y$b=6$

Contestar: $−15$

Decimales

Decimales Redondos

46. Redondear$6.738$ al ⓐ centésimo ⓑ décimo ⓒ número entero más cercano.

Sumar y restar decimales

En los siguientes ejercicios, realice la operación indicada.

47. $−23.67+29.84$

Contestar: $6.17$

48. $54.3−100$

49. $79.38−(−17.598)$

Contestar: $96.978$

Multiplicar y dividir decimales

En los siguientes ejercicios, realice la operación indicada.

50. $(−2.8)(3.97)$

51. $(−8.43)(−57.91)$

Contestar: 488.1813

52. $(53.48)(10)$

53. $(0.563)(100)$

Contestar: $56.3$

54. $ \$ 118.35÷2.6$

55. $1.84÷(−0.8)$

Contestar: $−23$

Convertir decimales, fracciones y porcentajes

En los siguientes ejercicios, escribe cada decimal como fracción.

56. $\dfrac{13}{20}$

57. $−\dfrac{240}{25}$

Contestar: $−9.6$

En los siguientes ejercicios, convierte cada fracción a un decimal.

58. $−\dfrac{5}{8}$

59. $\dfrac{14}{11}$

Contestar: $1.\overline{27}$

En los siguientes ejercicios, convertir cada decimal a un porcentaje.

60. $2.43$

61. $0.0475$

Contestar: $4.75 \% $

Simplifique las expresiones con raíces cuadradas

En los siguientes ejercicios, simplifique.

62. $\sqrt{289}$

63. $\sqrt{−121}$

Contestar: sin número real

Identificar números enteros, números racionales, números irracionales y números reales

En el siguiente ejercicio, enumere los ⓐ números enteros ⓑ enteros ⓒ números racionales ⓓ números irracionales ⓔ números reales para cada conjunto de números

64. $−8,0,1.95286...,\dfrac{12}{5},\sqrt{36},9$

Localizar fracciones y decimales en la línea numérica

En los siguientes ejercicios, ubique los números en una recta numérica.

65. $\dfrac{3}{4},−\dfrac{3}{4},1\dfrac{1}{3},−1\dfrac{2}{3},\dfrac{7}{2},−\dfrac{5}{2}$

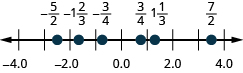
Contestar: $La figura muestra una línea numérica con números que van de menos 4 a 4. Se resaltan algunos valores.$

66. ⓐ$3.2$ ⓑ$−1.35$

Propiedades de Números Reales

Utilizar las propiedades conmutativas y asociativas

En los siguientes ejercicios, simplifique.

67. $\dfrac{5}{8}x+\dfrac{5}{12}y+\dfrac{1}{8}x+\dfrac{7}{12}y$

Contestar: $\dfrac{3}{4}x+y$

68. $−32·9·\dfrac{5}{8}$

69. $\left(\dfrac{11}{15}+\dfrac{3}{8}\right)+\dfrac{5}{8}$

Contestar: $1\dfrac{11}{15}$

Utilizar las Propiedades de Identidad, Inversa y Cero

En los siguientes ejercicios, simplifique.

70. $\dfrac{4}{7}+\dfrac{8}{15}+\left(−\dfrac{4}{7}\right)$

71. $\dfrac{13}{15}·\dfrac{9}{17}·\dfrac{15}{13}$

Contestar: $\dfrac{9}{17}$

72. $\dfrac{0}{x−3},x\neq 3$

73. $\dfrac{5x−7}{0},5x−7\neq 0$

Contestar: undefined

Simplificar expresiones mediante la propiedad distributiva

En los siguientes ejercicios, simplifique el uso de la Propiedad Distributiva.

74. $8(a−4)$

75. $12\left(\dfrac{2}{3}b+\dfrac{5}{6}\right)$

Contestar: $8b+10$

76. $18·\dfrac{5}{6}(2x−5)$

77. $(x−5)p$

Contestar: $xp−5p$

78. $−4(y−3)$

79. $12−6(x+3)$

Contestar: $−6x−6$

80. $6(3x−4)−(−5)$

81. $5(2y+3)−(4y−1)$

Contestar: $y+16$

Prueba de práctica

1. Encuentra la factorización principal de$756$.

2. Combina términos similares:$5n+8+2n−1$

Contestar: $7n+7$

3. Evaluar cuándo$x=−2$ y$y=3: \dfrac{|3x−4y|}{6}$

4. Traduzca a una expresión algebraica y simplifique:

ⓐ once menos que ocho negativos

ⓑ la diferencia de$−8$ y$−3$, incrementada en 5

Contestar: $−8−11 = −19$
$(−8−(−3))+5 = 0$

5. Dushko tiene monedas de cinco centavos y centavos en el bolsillo. El número de centavos es siete menos de cuatro veces el número de centavos. Que nn represente el número de monedas de cinco centavos. Escribe una expresión para el número de centavos.

6. Redondear$28.1458$ al más cercano

ⓐ centésima ⓑ milésima

Contestar: ⓐ$28.15$ ⓑ$28.146$

7. Convertir

ⓐ$\dfrac{5}{11}$ a un decimal ⓑ$1.15$ a un porcentaje

8. Localizar$\dfrac{3}{5},2.8,and−\dfrac{5}{2}$ en una línea numérica.

Contestar: $alt$

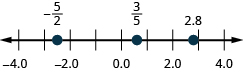
En los siguientes ejercicios, simplifique cada expresión.

9. $8+3[6−3(5−2)]−4^2$

10. $−(4−9)−(9−5)$

Contestar: 1

11. $56÷(−8)+(−27)÷(−3)$

12. $16−2|3(1−4)−(8−5)|$

Contestar: $−8$

13. $−5+2(−3)^2−9$

14. $\dfrac{180}{204}$

Contestar: $\dfrac{15}{17}$

15. $−\dfrac{7}{18}+\dfrac{5}{12}$

16. $\dfrac{4}{5}÷(−\dfrac{12}{25})$

Contestar: $−\dfrac{5}{3}$

17. $\dfrac{9−3·9}{15−9}$

18. $\dfrac{4(−3+2(3−6))}{3(11−3(2+3))}$

Contestar: $3$

19. $\dfrac{5}{13}⋅\dfrac{4}{7}⋅\dfrac{13}{5}$

20. $\dfrac{−\dfrac{5}{9}}{\dfrac{10}{21}}$

Contestar: $−\dfrac{7}{6}$

21. $−4.8+(−6.7)$

22. $34.6−100$

Contestar: $−65.4$

23. $−12.04⋅(4.2)$

24. $−8÷0.05$

Contestar: 160

25. $−\sqrt{121}$

26. $(\dfrac{8}{13}+\dfrac{5}{7})+\dfrac{2}{7}$

Contestar: $1\dfrac{8}{13}$

27. $5x+(−8y)−6x+3y$

28. ⓐ$\dfrac{0}{9}$ ⓑ$\dfrac{11}{0}$

Contestar: ⓐ 0 ⓑ undefined

29. $−3(8x−5)$

30. $6(3y−1)−(5y−3)$

Contestar: $13y−3$

Search

Text Color

Text Size

Margin Size

Font Type