2.6E: Ejercicios

Última actualización
Guardar como PDF

Page ID: 112744

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

La práctica hace la perfección

Graficar desigualdades en la recta numérica

En los siguientes ejercicios, grafica cada desigualdad en la recta numérica y escribe en notación de intervalos.

1. ⓐ$x<−2$
ⓑ$x\geq −3.5$
ⓒ$x\leq \frac{2}{3}$

2. ⓐ$x>3$
ⓑ$x\leq −0.5$
ⓒ$x\geq \frac{1}{3}$

Contestar

ⓐ

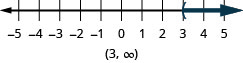
$La solución para x es mayor que 3 en una recta numérica tiene un corchete izquierdo 3 con sombreado a la derecha. La solución en la notación de intervalos es de 3 a infinito entre paréntesis.$

ⓑ

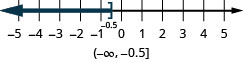
$La solución para x es menor o igual a negativo 0.5 en una recta numérica tiene un corchete derecho en negativo 0.5 con sombreado a la izquierda. La solución en notación de intervalos es de infinito negativo a negativo 0.5 dentro de un paréntesis y un paréntesis.$

ⓒ

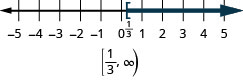
$La solución para x es mayor o igual a un tercio en una recta numérica tiene un corchete izquierdo en un tercio con sombreado a la derecha. La solución en la notación de intervalos es de un tercio al infinito dentro de un paréntesis y un paréntesis.$

3. ⓐ$x\geq −4$
ⓑ$x<2.5$
ⓒ$x>−\frac{3}{2}$

4. ⓐ$x\leq 5$
ⓑ$x\geq −1.5$
ⓒ$x<−\frac{7}{3}$

Contestar

ⓐ

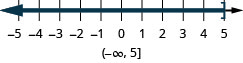
$La solución para x es menor o igual a 5 en una recta numérica tiene un corchete derecho con sombreado a la izquierda. La solución en notación de intervalos es infinito negativo a 5 dentro de un paréntesis y un paréntesis.$

ⓑ

$La solución para x es mayor o igual a negativo 1.5 en una recta numérica tiene un corchete izquierdo con sombreado a la derecha. La solución en notación de intervalos es negativa 1.5 a infinito dentro de un paréntesis y un paréntesis.$

ⓒ

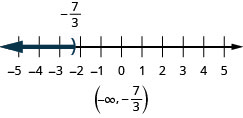
$La solución para x es menor que siete tercios negativos en una recta numéricamente tiene un paréntesis derecho con sombreado a la izquierda. La solución en notación de intervalos es de infinito negativo a siete tercios negativos entre paréntesis.$

5. ⓐ$−5<x<2$
ⓑ$−3\leq x<−1$
ⓒ$0\leq x\leq 1.5$

6. ⓐ$−2<x<0$
ⓑ$−5\leq x<−3$
ⓒ$0\leq x\leq 3.5$

Contestar

ⓐ

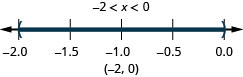
$Negativo 2 es menor que x que es menor que 0. Hay un círculo abierto en negativo 2 y un círculo abierto en 0 y sombreado entre negativo 2 y 0 en la recta numérica. La notación de intervalo es negativa 2 y 0 entre paréntesis.$

ⓑ

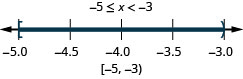
$Negativo 5 es menor o igual a x que es menor que negativo 3. Hay un círculo cerrado en negativo 5 y un círculo abierto en negativo 3 y sombreado entre negativo 5 y negativo 3 en la recta numérica. La notación de intervalo es negativa 5 y negativa 3 dentro de un paréntesis y un paréntesis.$

ⓒ

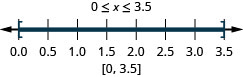
$0 es menor o igual a x que es menor o igual a 3.5. Hay un círculo cerrado en 0 y un círculo cerrado en 3.5 y sombreado entre 0 y 3.5 en la recta numérica. La notación de intervalo es 0 y 3.5 entre paréntesis.$

7. ⓐ$−1<x<3$
ⓑ$−3<x\leq −2$
ⓒ$−1.25\leq x\leq 0$

8. ⓐ$−4<x<2$
ⓑ$−5<x\leq −2$
ⓒ$−3.75\leq x\leq 0$

Contestar

ⓐ

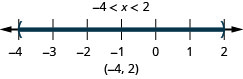
$Negativo 4 es menor que x que es menor que 2. Hay un círculo abierto en negativo 4 y un círculo abierto en 2 y sombreado entre negativo 4 y 2 en la recta numérica. La notación de intervalo es negativa 4 y 2 entre paréntesis.$

ⓑ

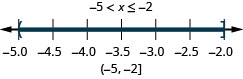
$Negativo 5 es menor que x que es menor o igual a 2. Hay un círculo abierto en negativo 5 y un círculo cerrado en negativo 2 y sombreado entre negativo 5 y negativo 2 en la recta numérica. La notación de intervalo es negativa 5 y negativa 2 dentro de un paréntesis y un paréntesis.$

ⓒ

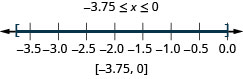
$Negativo 3.75 es menor o igual a x que es menor o igual a 0. Hay un círculo cerrado en negativo 3.75 y un círculo cerrado en 0 y sombreado entre negativo 3.75 y 0 en la recta numérica. La notación de intervalo es negativa 3.75 y 0 entre paréntesis.$

Resolver desigualdades lineales

En los siguientes ejercicios, resuelve cada desigualdad, grafica la solución en la recta numérica y escribe la solución en notación de intervalos.

9. ⓐ$a+\frac{3}{4}\geq \frac{7}{10}$
ⓑ$8x>72$
ⓒ$20>\frac{2}{5}h$

10. ⓐ$b+\frac{7}{8}\geq \frac{1}{6}$
ⓑ$6y<48$
ⓒ$40<\frac{5}{8}k$

Contestar

ⓐ

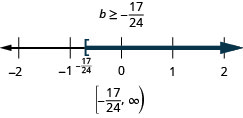
$La solución es b es mayor o igual a diecisiete veinticuartas partes negativas. La solución en una recta numérica tiene un paréntesis izquierdo negativo diecisiete veinticuartas partes con sombreado a la derecha. La solución en notación de intervalos es de diecisiete veinticinco cuartas partes al infinito dentro de un paréntesis y un paréntesis.$

ⓑ

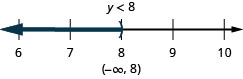
$La solución es y es menor que 8. La solución en una recta numérica tiene un paréntesis derecho en 8 con sombreado a la izquierda. La solución en la notación de intervalos es infinito negativo a 8 entre paréntesis.$

ⓒ

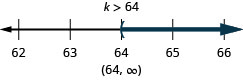
$La solución es k es mayor que 64. La solución en una recta numérica tiene un paréntesis izquierdo en 64 con sombreado a la derecha. La solución en notación de intervalos es de 64 a infinito entre paréntesis.$

11. ⓐ$f−\frac{13}{20}<−\frac{5}{12}$
ⓑ$9t\geq −27$
ⓒ$\frac{7}{6}j\geq 42$

12. ⓐ$g−\frac{11}{12}<−\frac{5}{18}$
ⓑ$7s<−28$
ⓒ$\frac{9}{4}g\leq 36$

Contestar

ⓐ

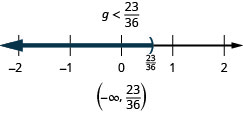
$La solución es g es menor a veintitrés treinta y sextos. La solución en una recta numérica tiene un paréntesis derecho a los veintitrés treinta y seis con sombreado a la izquierda. La solución en notación de intervalos es infinito negativo a veintitrés treinta y sextos entre paréntesis.$

ⓑ

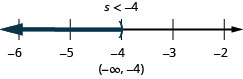
$La solución es s es menor que negativa 4. La solución en una recta numérica tiene un paréntesis derecho en negativo 4 con sombreado a la izquierda. La solución en la notación de intervalos es de infinito negativo a negativo 4 entre paréntesis.$

ⓒ

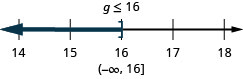
$La solución es g es menor o igual a 16. La solución en una recta numérica tiene un corchete derecho en 16 con sombreado a la izquierda. La solución en notación de intervalos es infinito negativo a 16 entre paréntesis y un corchete.$

13. ⓐ$−5u\geq 65$
ⓑ$\frac{a}{−3}\leq 9$

14. ⓐ$−8v\leq 96$
ⓑ$\frac{b}{−10}\geq 30$

Contestar

ⓐ

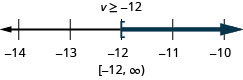
$La solución es v es mayor o igual a negativo 12. La solución en una recta numérica tiene un corchete izquierdo con sombreado a la derecha. La solución en notación de intervalos es negativa 12 a infinito dentro de un paréntesis y un paréntesis.$

ⓑ

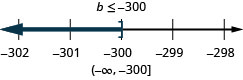
$La solución es b es menor o igual a negativo 300. La solución en una recta numérica tiene un corchete derecho en negativo 300 con sombreado a la izquierda. La solución en notación de intervalos es de infinito negativo a negativo 300 dentro de un paréntesis y un paréntesis.$

15. ⓐ$−9c<126$
ⓑ$−25<\frac{p}{−5}$

16. ⓐ$−7d>105$
ⓑ$−18>\frac{q}{−6}$

Contestar

ⓐ

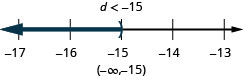
$La solución es d es menor que negativa 15. La solución en una recta numérica tiene un paréntesis derecho con sombreado a la izquierda. La solución en notación de intervalos es de infinito negativo a negativo 15 entre paréntesis.$

ⓑ

$La solución es q es mayor que 108. La solución en una recta numérica tiene paréntesis a la izquierda en 108 con sombreado a la derecha. La solución en notación de intervalos es de 108 a infinito entre paréntesis.$

En los siguientes ejercicios, resuelve cada desigualdad, grafica la solución en la recta numérica y escribe la solución en notación de intervalos.

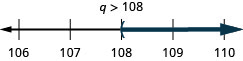
17. $4v\geq 9v−40$

18. $5u\leq 8u−21$

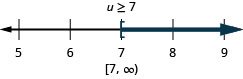
Contestar: $La solución es u es mayor o igual a 7. La solución en una recta numérica tiene un corchete izquierdo en 7 con sombreado a la derecha. La solución en notación de intervalos es de 7 a infinito dentro de un paréntesis y un paréntesis.$

19. $13q<7q−29$

20. $9p>14p−18$

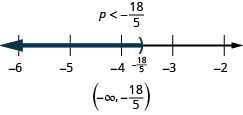
Contestar: $La solución es p es menor a dieciocho quintas partes. La solución en una recta numérica tiene un paréntesis derecho a las dieciocho quintas partes con sombreado a la izquierda. La solución en notación de intervalo infinito negativo a dieciocho quintos entre paréntesis.$

21. $12x+3(x+7)>10x−24$

22. $9y+5(y+3)<4y−35$

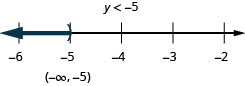
Contestar: $La solución es y es menor que negativa 5. La solución en una recta numérica tiene un paréntesis derecho en negativo 5 con sombreado a la izquierda. La solución en notación de intervalos es de infinito negativo a negativo 5 entre paréntesis.$

23. $6h−4(h−1)\leq 7h−11$

24. $4k−(k−2)\geq 7k−26$

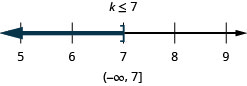
Contestar: $La solución es k es menor o igual a 7. La solución en una recta numérica tiene un corchete derecho en 7con sombreado a la izquierda. La solución en notación de intervalos es infinito negativo a 7 dentro de un paréntesis y un paréntesis.$

25. $8m−2(14−m)\geq 7(m−4)+3m$

26. $6n−12(3−n)\leq 9(n−4)+9n$

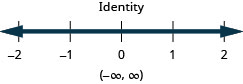
Contestar: $La desigualdad es una identidad. Su solución en la recta numérica está sombreada para todos los valores. La solución en la notación de intervalos es infinito negativo a infinito entre paréntesis.$

27. $\frac{3}{4}b−\frac{1}{3}b<\frac{5}{12}b−\frac{1}{2}$

28. $9u+5(2u−5)\geq 12(u−1)+7u$

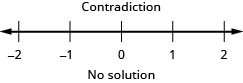
Contestar: $La desigualdad es una contradicción. Entonces, no hay solución. Como resultado, no hay gráfico en la línea numérica o notación de intervalo.$

29. $\frac{2}{3}g−\frac{1}{2}(g−14)\leq \frac{1}{6}(g+42)$

30. $\frac{4}{5}h−\frac{2}{3}(h−9)\geq \frac{1}{15}(2h+90)$

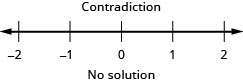
Contestar: $La desigualdad es una contradicción. Entonces, no hay solución. Como resultado, no hay gráfico en la línea numérica o notación de intervalo.$

31. $\frac{5}{6}a−\frac{1}{4}a>\frac{7}{12}a+\frac{2}{3}$

32. $12v+3(4v−1)\leq 19(v−2)+5v$

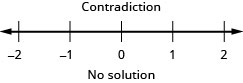
Contestar: $La desigualdad es una contradicción. Entonces, no hay solución. Como resultado, no hay gráfico en la línea numérica o notación de intervalo.$

En los siguientes ejercicios, resuelve cada desigualdad, grafica la solución en la recta numérica y escribe la solución en notación de intervalos.

33. $15k\leq −40$

34. $35k\geq −77$

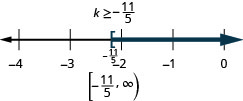
Contestar: $La solución es k es mayor o igual a once quintas negativas. La solución en una recta numérica tiene un paréntesis izquierdo en once quintos negativos con sombreado a la derecha. La solución en notación de intervalos es de once quintos negativos a infinito negativo dentro de un paréntesis y un paréntesis.$

35. $23p−2(6−5p)>3(11p−4)$

36. $18q−4(10−3q)<5(6q−8)$

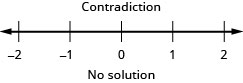
Contestar: $La desigualdad es una contradicción. Entonces, no hay solución. Como resultado, no hay gráfico en la línea numérica o notación de intervalo.$

37. $−\frac{9}{4}x\geq −\frac{5}{12}$

38. $−\frac{21}{8}y\leq −\frac{15}{28}$

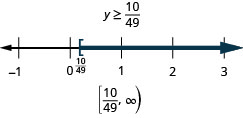
Contestar: $La solución es y es mayor o igual a diez veintinueve. La solución en una recta numérica tiene un corchete izquierdo a las diez veintinueve con sombreado a la derecha. La solución en notación de intervalos es de diez veintinueve a infinito dentro de un paréntesis y un paréntesis.$

39. $c+34<−99$

40. $d+29>−61$

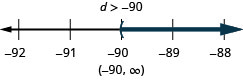
Contestar: $La solución es g es mayor que negativa 90. La solución en una recta numérica tiene un paréntesis izquierdo en negativo 90 con sombreado a la derecha. La solución en la notación de intervalos es de 90 a infinito entre paréntesis.$

41. $\frac{m}{18}\geq −4$

42. $\frac{n}{13}\leq −6$

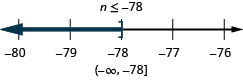
Contestar: $La solución es n es menor o igual a negativo 78. La solución en una recta numérica tiene un corchete derecho en negativo 78 con sombreado a la izquierda. La solución en notación de intervalos es de infinito negativo a negativo 78 dentro de un paréntesis y un paréntesis.$

Traducir a una desigualdad y resolver

En los siguientes ejercicios, traduzca y resuelva. Luego grafica la solución en la recta numérica y escribe la solución en notación de intervalos.

43. Tres más de lo que no$h$ es menor que$25$.

44. Seis más que$k$ supera$25$.

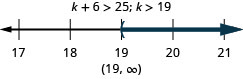
Contestar: $La desigualdad es k más 6 es mayor que 25. Su solución es k es mayor que 19. La solución en una recta numérica tiene un paréntesis izquierdo en 19 con sombreado a la derecha. La solución en la notación de intervalos es de 19 a infinito entre paréntesis.$

45. Diez menos de lo que$w$ es al menos$39$.

46. Doce menos de lo que no$x$ es menor que$21$.

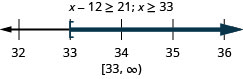
Contestar: $La desigualdad es x menos 12 es mayor o igual a 21. Su solución es x es mayor o igual a 33. La solución en una recta numérica tiene un corchete izquierdo en 33 con sombreado a la derecha. La solución en notación de intervalos es de 33 a infinito dentro de un paréntesis y un paréntesis.$

47. Negativo cinco veces no$r$ es más que$95$.

48. Negativo dos veces$s$ es menor que$56$.

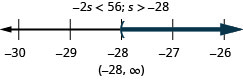
Contestar: $La desigualdad es negativa 2 s es menor que 56. Su solución es s es mayor que negativa 28. La solución en una recta numérica tiene un paréntesis izquierdo en 28 negativo con sombreado a la derecha. La solución en la notación de intervalos es de 28 a infinito entre paréntesis.$

49. Diecinueve menos de lo que$b$ es como mucho$−22$.

50. Quince menos de lo que$a$ es por lo menos$−7$.

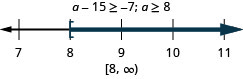
Contestar: $La desigualdad es un menos 15 es mayor o igual a negativo 7. Su solución es a es mayor o igual a 8. La solución en una recta numérica tiene un corchete izquierdo en 8 con sombreado a la derecha. La solución en notación de intervalos es de 8 a infinito dentro de un paréntesis y un paréntesis.$

Resolver aplicaciones con desigualdades lineales

En los siguientes ejercicios, resuelve.

51. Alan está cargando una tarima con cajas que pesan 45 libras cada una. El palé puede soportar de manera segura no más de 900 libras. ¿Cuántas cajas puede cargar de manera segura en el palé?

52. El elevador en el edificio de departamentos de Yehire tiene un letrero que dice que el peso máximo es de 2100 libras. Si el peso promedio de una persona es de 150 libras, ¿cuántas personas pueden viajar con seguridad en el elevador?

Contestar: Un máximo de 14 personas pueden viajar con seguridad en el elevador.

53. Andre está buscando departamentos con tres de sus amigos. Quieren que la renta mensual no sea superior a $2,360. Si los compañeros de cuarto dividen la renta de manera uniforme entre los cuatro, ¿cuál es la renta máxima que pagará cada uno?

54. Arleen obtuvo una tarjeta de regalo de $20 para la cafetería. Su bebida helado favorita cuesta 3.79 dólares. ¿Cuál es el número máximo de bebidas que puede comprar con la tarjeta regalo?

Contestar: cinco tragos

55. A Teegan le gusta jugar al golf. Ha presupuestado 60 dólares el próximo mes para el campo de prácticas. Le cuesta 10.55 dólares por un cubo de bolas cada vez que va. ¿Cuál es el número máximo de veces que puede ir al campo de prácticas el próximo mes?

56. Ryan cobra a sus vecinos 17.50 dólares para lavar su auto. ¿Cuántos autos debe lavar el próximo verano si su objetivo es ganar al menos $1,500?

Contestar: 86 autos

57. A Keshad se le pagan 2.400 dólares mensuales más 6% de sus ventas. Su hermano gana 3.300 dólares mensuales. ¿Por qué cantidad de ventas totales será mayor el pago mensual de Keshad que el pago mensual de su hermano?

58. Kimuyen necesita ganar $4,150 mensuales para poder pagar todos sus gastos. Su trabajo le paga $3,475 mensuales más 4% de sus ventas totales. ¿Cuál es el mínimo que deben ser las ventas totales de Kimuyen para que pueda pagar todos sus gastos?

Contestar: $16,875

59. A Andre se le ha ofrecido un trabajo de nivel de entrada. La compañía le ofreció 48,000 dólares anuales más 3.5% de sus ventas totales. Andre sabe que el salario promedio para este empleo es de $62,000. ¿Cuáles necesitarían ser las ventas totales de Andre para que su salario sea al menos tan alto como el salario promedio para este trabajo?

60. Nataly está considerando dos ofertas de trabajo. El primer trabajo le pagaría 83,000 dólares anuales. El segundo le pagaría 66,500 dólares más el 15% de sus ventas totales. ¿Cuáles necesitarían ser sus ventas totales para que su salario en la segunda oferta sea superior al primero?

Contestar: $110,000

61. La factura de agua de Jake es de 24.80 dólares mensuales más $2.20 por ccf (cien pies cúbicos) de agua. ¿Cuál es el número máximo de ccf que Jake puede usar si quiere que su factura no sea superior a los 60 dólares?

62. El plan telefónico de Kiyoshi cuesta $17.50 mensuales más $0.15 por mensaje de texto. ¿Cuál es el número máximo de mensajes de texto que Kiyoshi puede usar para que la factura telefónica no supere los $56.60?

Contestar: 260 mensajes

63. El plan de televisión de Marlon cuesta $49.99 mensuales más $5.49 por película de primera ejecución. ¿Cuántas películas de estreno puede ver si quiere mantener su factura mensual para que sea de un máximo de $100?

64. Kellen quiere rentar una sala de banquetes en un restaurante para el baby shower de su prima. El restaurante cobra $350 por el salón de banquetes más $32.50 por persona para el almuerzo. ¿Cuántas personas puede tener Kellen en la ducha si quiere que el costo máximo sea de $1,500?

Contestar: 35 personas

65. Moshde dirige un negocio de peluquería desde su casa. Ella cobra 45 dólares por un corte de pelo y estilo. Sus gastos mensuales son $960. Ella quiere poder poner al menos $1,200 mensuales en su orden de cuenta de ahorros para abrir su propio salón. ¿Cuántos “cortes y estilos” debe hacer para ahorrar al menos $1,200 mensuales?

66. Noe instala y configura software en computadoras domésticas. Él cobra 125 dólares por trabajo. Sus gastos mensuales son de $1,600. ¿Cuántos empleos debe trabajar para obtener una ganancia de al menos 2.400 dólares?

Contestar: 32 empleos

67. Katherine es una chef personal. Ella cobra 115 dólares por comida para cuatro personas. Sus gastos mensuales son de $3,150. ¿Cuántas comidas para cuatro personas debe vender para obtener una ganancia de al menos $1,900?

68. Melissa hace collares y los vende en línea. Ella cobra $88 por collar. Sus gastos mensuales son de $3,745. ¿Cuántos collares debe vender si quiere obtener una ganancia de al menos $1,650?

Contestar: 62 collares

69. Cinco funcionarios estudiantiles del gobierno quieren ir a la convención estatal. Les costará $110 por registro, $375 para transporte y comida, y $42 por persona para el hotel. Hay 450 dólares presupuestados para la convención en la cuenta de ahorro del gobierno estudiantil. Pueden ganar el resto del dinero que necesitan al tener un lavado de autos. Si cobran $5 por auto, ¿cuántos autos deben lavar para tener suficiente dinero para pagar el viaje?

70. César está planeando un viaje de cuatro días para visitar a su amigo en una universidad en otro estado. Le costará 198 dólares por pasajes aéreos, 56 dólares por transporte local y 45 dólares diarios por comida. Tiene 189 dólares en ahorros y puede ganar 35 dólares por cada césped que corte. ¿Cuántos céspedes debe cortar para tener suficiente dinero para pagar el viaje?

Contestar: siete céspedes

71. Alonzo trabaja como detallista de autos. Él cobra 175 dólares por auto. Planea mudarse de la casa de sus padres y rentar su primer departamento. Tendrá que pagar 120 dólares por las tasas de solicitud, 950 dólares por depósito de seguridad y la renta del primer y último mes a $1,140 mensuales. Cuenta con $1,810 en ahorros. ¿Cuántos autos debe detallar para tener el dinero suficiente para rentar el departamento?

72. Eun-Kyung trabaja como tutor y gana 60 dólares por hora. Ella tiene $792 en ahorros. Ella está planeando una fiesta de aniversario para sus padres. A ella le gustaría invitar a 40 invitados. La fiesta le costará $1,520 por comida y bebida y $150 para la fotógrafa. Ella también tendrá un favor para cada uno de los invitados, y cada favor costará $7.50. ¿Cuántas horas debe ser tutora para tener suficiente dinero para la fiesta?

Contestar: 20 horas

Matemáticas cotidianas

73. Carga máxima en un escenario En 2014, un escenario de secundaria colapsó en Fullerton, California, cuando 250 estudiantes subieron al escenario para el final de una producción musical. Dos docenas de estudiantes resultaron heridos. El escenario podría soportar un máximo de 12,750 libras. Si se supone que el peso promedio de un estudiante es de 140 libras, ¿cuál es el número máximo de estudiantes que podrían estar en el escenario con seguridad?

74. Peso máximo en un barco En 2004, un taxi acuático se hundió en el puerto de Baltimore y cinco personas se ahogaron. El taxi acuático tenía una capacidad máxima de 3,500 libras (25 personas con peso promedio 140 libras). El peso promedio de las 25 personas en el taxi acuático cuando se hundió era de 168 libras por persona. ¿Cuál debería haber sido el número máximo de personas de este peso?

Contestar: 20 personas

75. Presupuesto para bodas Adele y Walter encontraron el lugar perfecto para la recepción de su boda. El costo es de $9850 para un máximo de 100 invitados, más $38 por cada huésped adicional. ¿Cuántos invitados pueden asistir si Adele y Walter quieren que el costo total no sea superior a 12.500 dólares?

76. Presupuesto de ducha Penny está planeando un baby shower para su nuera. El restaurante cobra $950 por hasta 25 invitados, más $31.95 por cada huésped adicional. ¿Cuántos invitados pueden asistir si Penny quiere que el costo total no sea superior a $1,500?

Contestar: 42 invitados

Ejercicios de escritura

77. Explique por qué es necesario revertir la desigualdad a la hora de resolver$−5x>10$.

78. Explique por qué es necesario revertir la desigualdad a la hora de resolver$n−3<12$.

Contestar: Las respuestas variarán.

79. Encuentra tu factura telefónica del último mes y el salario por hora que te pagan en tu trabajo. Calcula el número de horas de trabajo que te llevaría ganar al menos el dinero suficiente para pagar tu factura telefónica escribiendo una desigualdad apropiada y luego resolviéndola. ¿Sientes que este es un número apropiado de horas? ¿Este es el plan telefónico adecuado para ti?

80. Entérate de cuántas unidades te quedan, después de este término, para lograr tu meta universitaria y estima el número de unidades que puedes tomar cada trimestre en la universidad. Calcula el número de términos que te llevará lograr tu objetivo universitario escribiendo una desigualdad apropiada y luego resolviéndola. ¿Es este un número aceptable de términos hasta que cumpla con su objetivo? ¿Cuáles son algunas formas en las que podrías acelerar este proceso?

Contestar: Las respuestas variarán.

Autocomprobación

ⓐ Después de completar los ejercicios, usa esta lista de verificación para evaluar tu dominio de los objetivos de esta sección.

$Esta tabla tiene cuatro columnas y cinco filas. La primera fila es un encabezado y etiqueta a cada columna, “Puedo...”, “Con confianza”, “Con algo de ayuda” y “¡No-I don't get it!” En la fila 2, el yo puedo fue graficar desigualdades en la recta numérica. En la fila 3, lo que puedo fue resolver desigualdades lineales. En la fila 4, lo que puedo fue traducir palabras a una desigualdad y resolver. En la fila 5, lo que puedo fue resolver aplicaciones con desigualdades lineales.$

ⓑ Después de mirar la lista de verificación, ¿crees que estás bien preparado para la siguiente sección? ¿Por qué o por qué no?