2.6: Resolver desigualdades lineales

Última actualización
Guardar como PDF

Page ID: 112739

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Objetivos de aprendizaje

Al final de esta sección, podrás:

Graficar desigualdades en la recta numérica
Resolver desigualdades lineales
Traducir palabras a una desigualdad y resolver
Resolver aplicaciones con desigualdades lineales

Antes de comenzar, toma este cuestionario de preparación.

Traducir del álgebra al inglés:$15>x$.
Si te perdiste este problema, revisa [enlace].
Traducir a una expresión algebraica:$15$ es menor que$x$.
Si te perdiste este problema, revisa [enlace].

Graficar desigualdades en la recta numérica

¿Qué número haría$x>3$ verdadera la desigualdad? ¿Estás pensando, "$x$podrían ser cuatro”? Eso es correcto, pero$x$ podría ser 6, también, o 37, o incluso 3.001. Cualquier número mayor a tres es una solución a la desigualdad$x>3$. Mostramos todas las soluciones a la desigualdad$x>3$ en la recta numérica sombreando todos los números a la derecha de tres, para mostrar que todos los números mayores a tres son soluciones. Debido a que el número tres en sí no es una solución, ponemos un paréntesis abierto a las tres.

También podemos representar desigualdades usando notación de intervalos. No hay un extremo superior para la solución a esta desigualdad. En notación de intervalos, expresamos$x>3$ como$(3,\infty)$. El símbolo$\infty$ se lee como “infinito”. No es un número real. La figura$\PageIndex{1}$ muestra tanto la línea numérica como la notación de intervalo.

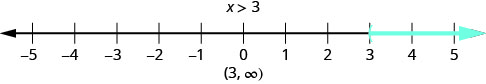
La figura muestra la incalidad, x es mayor que 3, graficada en una recta numérica de 5 a 5. Hay sombreado que comienza en 3 y se extiende a números a su derecha. La solución para la desigualdad está escrita en notación de intervalos. Es el intervalo de 3 a infinito, sin incluir 3. — Figura$\PageIndex{1}$: La desigualdad$x>3$ se grafica en esta recta numérica y se escribe en notación de intervalos.

Utilizamos el símbolo de paréntesis izquierdo, (, para mostrar que no se incluye el punto final de la desigualdad. El símbolo de corchete izquierdo, [, muestra que el punto final está incluido.

La desigualdad$x\leq 1$ significa todos los números menores o iguales a uno. Aquí tenemos que demostrar que una es una solución, también. Eso lo hacemos poniendo un soporte en$x=1$. Luego sombreamos todos los números a la izquierda de uno, para mostrar que todos los números menores de uno son soluciones (Figura$\PageIndex{2}$). No hay un extremo inferior para esos números. Escribimos$x\leq 1x\leq 1 $ en notación de intervalos como$(−\infty,1]$. El símbolo$−\infty$ se lee como “infinito negativo”.

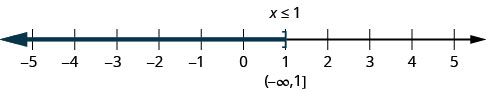
La figura muestra la incalidad, x es menor o igual a l, graficada en una recta numérica de 5 a 5 negativo. Hay sombreado que comienza en 1 y se extiende a números a su izquierda. La solución para la desigualdad está escrita en notación de intervalos. Es el intervalo de infinito negativo a uno, incluyendo 1. — Figura$\PageIndex{2}$: La desigualdad$x\leq 1$ se grafica en esta recta numérica y se escribe en notación de intervalos.

La figura$\PageIndex{3}$ muestra tanto la línea numérica como la notación de intervalo.

Desigualdades, líneas numéricas y notación de intervalos

$La figura muestra que la solución de la desigualdad x es mayor que a se indica en una recta numérica con un paréntesis izquierdo en a y sombreado a la derecha, y que la solución en notación de intervalo es el intervalo de a a infinito encerrado entre paréntesis. Se muestra que la solución de la desigualdad x es mayor o igual que a se indica en una recta numérica con un paréntesis izquierdo en a y sombreado a la derecha, y que la solución en notación de intervalo es el intervalo a al infinito dentro de un paréntesis izquierdo y paréntesis derecho. Se muestra que la solución de la desigualdad x es menor que a se indica en una recta numérica con un paréntesis derecho en a y sombreado a la izquierda, y que la solución en notación de intervalo es el intervalo infinito negativo a a entre paréntesis. Se muestra que la solución de la desigualdad x es menor o igual a a se indica en la línea anumber con un corchetes derecho en a y sombreado a la izquierda, y que la solución en notación de intervalo es infinito negativo a a dentro de un paréntesis izquierdo y corchetes derecho.$

La notación de desigualdades en una recta numérica y en notación de intervalo usa los mismos símbolos para expresar los puntos finales de los intervalos.

Ejemplo$\PageIndex{1}$

Grafica cada desigualdad en la recta numérica y escribe en notación de intervalos.

$x\geq −3$
$x<2.5$
$x\leq −\frac{3}{5}$

Responder

ⓐ

	$ x \geq -3 $
Sombra a la derecha de$−3$, y coloque un soporte en$−3$.	$.$
Escribir en notación de intervalos.	$ [-3, \infty) $

ⓑ

	$ x < 2.5 $
Sombra a la izquierda de 2.5 y ponga un paréntesis en 2.5.	$.$
Escribir en notación de intervalos.	$ (-\infty, 2.5) $

ⓒ

	$ x \leq -\dfrac{3}{5} $
Sombra a la izquierda de$−\frac{3}{5}$, y poner un soporte en$−\frac{3}{5}$.	$.$
Escribir en notación de intervalos.	$ \bigg( -\infty, \dfrac{3}{5}\bigg] $

Grafica cada desigualdad en la recta numérica y escribe en notación de intervalo:

$x>2$
$x\leq −1.5$
$x\geq \frac{3}{4}$.

Responder

ⓐ

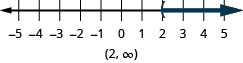
$El gráfico de la desigualdad x es mayor que 2 se indica en una recta numérica con paréntesis izquierdo en 2 y sombreado a la derecha. La solución en la notación de intervalos es el intervalo de 2 a infinito encerrado entre paréntesis.$

ⓑ

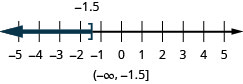
$El gráfico de la desigualdad x es menor o igual a negativo 1.5 se indica en una recta numérica con un corchetes derecho en negativo 1.5 y sombreado a la izquierda. La solución en la notación de intervalos es el intervalo de infinito negativo a negativo 1.5 encerrado entre paréntesis izquierdo y corchetes derecho.$

ⓒ

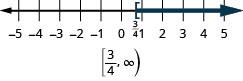
$La gráfica de la desigualdad x es mayor o rqual a tres cuartas partes se indica en una recta numérica con un corchetes izquierdo en tres cuartos y sombreado a la derecha. La solución en la notación de intervalos es el intervalo de tres cuartos a infinito encerrado dentro de un paréntesis izquierdo y paréntesis izquierdos.$

Ejemplo$\PageIndex{3}$

Grafica cada desigualdad en la recta numérica y escribe en notación de intervalo:

$x\leq −4$
$x\geq 0.5$
$x<−\frac{2}{3}$.

Responder

ⓐ

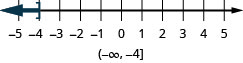
$El gráfico de la desigualdad x es menor o igual a negativo 4 se indica en una recta numérica con un corchetes derecho en negativo 4 y sombreado a la izquierda. La solución en la notación de intervalos es el intervalo de infinito negativo a negativo 4 encerrado dentro de un paréntesis izquierdo y corchetes derecho.$

ⓑ

$El gráfico de la desigualdad x es mayor o igual a 0.5 se indica en una recta numérica con un corchetes izquierdo en 0.5 y sombreado a la derecha. La solución en la notación de intervalos es el intervalo de 0.5 a infinito encerrado dentro de un paréntesis izquierdo y paréntesis derecho.$

ⓒ

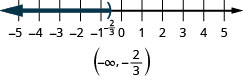
$El gráfico de la desigualdad x es menor que dos tercios negativos se indica en una recta numérica con un paréntesis derecho en dos tercios negativos y sombreado a la izquierda. La solución en la notación de intervalos es el intervalo de infinito negativo a dos tercios negativos encerrado entre paréntesis.$

¿Qué números son mayores que dos pero menores que cinco? ¿Estás pensando decir,$2.5,\space 3,\space 3\frac{2}{3},\space 4,\space 4,\space 99$? Podemos representar todos los números entre dos y cinco con la desigualdad$2<x<5$. Podemos mostrar$2<x<5$ en la recta numérica sombreando todos los números entre dos y cinco. Nuevamente, usamos los paréntesis para mostrar que los números dos y cinco no están incluidos. Ver Figura.

La gráfica de la desigualdad 2 es menor que x que es menor que 5 muestra los círculos abiertos a 2 y 5 y el sombreado entre ellos. — Figura$\PageIndex{3}$

Grafica cada desigualdad en la recta numérica y escribe en notación de intervalos.

ⓐ$−3<x<4$ ⓑ$−6\leq x<−1$ ⓒ$0\leq x\leq 2.5$

Responder

ⓐ

		$-3 < x < 4$
Sombra entre$−3$ y 4. Poner paréntesis en$−3$ y 4.		$.$
Escribir en notación de intervalos.		$ (-3,4) $

ⓑ

			$ -6 \leq x < -1 $
Sombra entre$−6$ y −1. Ponga un corchete en$−6$, y un paréntesis en −1.			$.$
Escribir en notación de intervalos.			$ [-6,1) $

ⓒ

			$ 0 \leq x \leq 2.5 $
Sombra entre 0 y 2.5. Poner un soporte en 0 y en 2.5.			$.$
Escribir en notación de intervalos.			$ [0, 2.5] $

Ejemplo$\PageIndex{5}$

Grafica cada desigualdad en la recta numérica y escribe en notación de intervalo:

ⓐ$−2<x<1$ ⓑ$−5\leq x<−4$ ⓒ$1\leq x\leq 4.25$

Responder

ⓐ

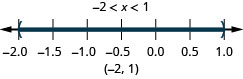
$Negativo 2 es menor x que es menor que 1. Hay círculos abiertos en negativo 2 y 1 y sombreado entre negativo 2 y 1 en la recta numérica. Poner paréntesis en negativo 2 y 1. Escribir en notación de intervalos.$

ⓑ

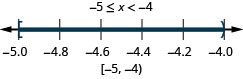
$Negativo 5 es menor o igual a x que es menor que negativo 4. Hay un círculo cerrado en negativo 6 y un círculo abierto en negativo 4 y sombreado entre negativo 5 y negativo 4 en la recta numérica. Poner un corchete en negativo 5 y un paréntesis en negativo 4. Escribir en notación de intervalos.$

ⓒ

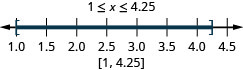
$1 es menor o igual a x que es menor que 4.25. Hay círculo cerrado en 1 y un círculo cerrado en 4.25 y sombreado entre 1 y 4.25 en la recta numérica. Ponga los soportes en 1 y 4.25. Escribir en notación de intervalos.$

Ejemplo$\PageIndex{6}$

Grafica cada desigualdad en la recta numérica y escribe en notación de intervalo:

ⓐ$−6<x<2$ ⓑ$−3\leq x< −1$ ⓒ$2.5\leq x\leq 6$

Responder

ⓐ

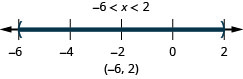
$Negativo 6 es menor que x que es menor que 2. Hay un círculo abierto en negativo 6 y un círculo abierto en 2 y sombreado entre negativo 6 y 2 en la recta numérica. Poner paréntesis en negativo 6 y 2. Escribir en notación de intervalos.$

ⓑ

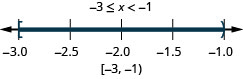
$Negativo 3 es menor o igual a x que es menor que negativo 1. Hay un círculo cerrado en negativo 3 y un círculo abierto en negativo 1 y sombreado entre negativo 3 y negativo 1 en la recta numérica. Poner un corchete en negativo 3 y un paréntesis en negativo 1. Escribir en notación de intervalos.$

ⓒ

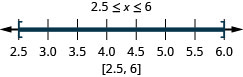
$2.5 es menor o igual a x que es menor queo igual a 6. Hay un círculo cerrado en 2.5 y un círculo cerrado en 6 y sombreado entre 2.5 y 6 en la recta numérica. Ponga los soportes en 2.5 y 6. Escribir en notación de intervalos.$

Resolver desigualdades lineales

Una desigualdad lineal es muy parecida a una ecuación lineal, pero el signo igual se reemplaza por un signo de desigualdad. Una desigualdad lineal es una desigualdad en una variable que se puede escribir en una de las formas,$ax+b<c$,$ax+b\leq c$,$ax+b>c$, o$ax+b\geq c$.

Desigualdad lineal

Una desigualdad lineal es una desigualdad en una variable que se puede escribir en una de las siguientes formas donde$a, \, b,$ y$c$ son números reales y$a≠0$:

\[ \begin{array} {llll} {ax+b<c,} &{ax+b\leq c,} &{ax+b>c,} &{ax+b\geq c.} \\ \nonumber \end{array}\]

Cuando resolvimos ecuaciones lineales, pudimos usar las propiedades de igualdad para sumar, restar, multiplicar o dividir ambos lados y aún así mantener la igualdad. Propiedades similares son ciertas para las desigualdades.

Podemos sumar o restar la misma cantidad de ambos lados de una desigualdad y aún así mantener la desigualdad. Por ejemplo:

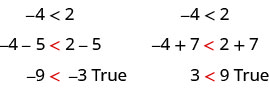
$Negativo 4 es menor que 2. Negativo 4 menos 5 es menor que 2 menos 5. Negativo 9 es menor que negativo 3, lo cual es cierto. Negativo 4 es menor que 2. Negativo 4 más 7 es menor que 2 más 7. 3 es menor que 9, lo cual es cierto.$

Observe que el signo de desigualdad se mantuvo igual.

Esto nos lleva a las Propiedades de Suma y Resta de la Desigualdad.

Suma y resta propiedad de desigualdad

Para cualquier número$a, \, b,$ y$c,$ si$a<b$, entonces

\[\begin{array} {ll} {a+c<b+c} &{a−c<b−c} \\ {a+c>b+c} &{a−c>b−c} \\ \nonumber \end{array}\]

Podemos sumar o restar la misma cantidad de ambos lados de una desigualdad y aún así mantener la desigualdad

¿Qué pasa con una desigualdad cuando dividimos o multiplicamos ambos lados por una constante?

Primero multipliquemos y dividamos ambos lados por un número positivo.

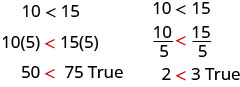
$10 es menor que 15. 10 veces 5 es menor que 15 veces 5. 50 es menor que 75 es verdadero. 10 es menor que 15. 10 dividido por 5 es menor que 15 dividido por 5. 2 es menor que 3 es verdadero.$

Los signos de desigualdad permanecieron igual.

¿La desigualdad permanece igual cuando dividimos o multiplicamos por un número negativo?

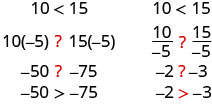
$10 es menor que 15 10 veces negativo 5 está en blanco 15 veces negativo 5? Negativo 50 es negativo en blanco 75. Negativo 50 es mayor que negativo 75. 10 es menor que 15. 10 dividido por negativo 5 es blanco 15 dividido por negativo 5. Negativo 2 es negativo en blanco 3. Negativo 2 es negativo en blanco 3.$

Observe que cuando llenamos los signos de desigualdad, los signos de desigualdad invirtieron su dirección.

Cuando dividimos o multiplicamos una desigualdad por un número positivo, el signo de desigualdad permanece igual. Cuando dividimos o multiplicamos una desigualdad por un número negativo, el signo de desigualdad se invierte.

Esto nos da la Propiedad de Multiplicación y División de la Desigualdad.

Multiplicación y división de propiedad de la desigualdad

Para cualquier número$a, \, b,$ y$c,$

\[\begin{array} {l} {\text{multiply or divide by a positive}} \\ \\ \space\space\space\space\text{if }a<b\text{ and }c>0\text{, then }ac<bc \text{ and }\frac{a}{c}<\frac{b}{c}. \\ \space\space\space\space\text{if }a>b\text{ and }c>0\text{, then }ac>bc \text{ and }\frac{a}{c}>\frac{b}{c}. \\ \\ \text{ multiply or divide by a negative } \\ \\ \space\space\space\space\text{if }a<b\text{ and }c<0\text{, then }ac>bc \text{ and }\frac{a}{c}>\frac{b}{c}.\\ \space\space\space\space\text{if }a>b\text{ and }c<0\text{, then }ac<bc \text{ and }\frac{a}{c}<\frac{b}{c}.\\ \nonumber \end{array}\]

Cuando dividimos o multiplicamos una desigualdad por$a$:

número positivo, la desigualdad se mantiene igual.
número negativo, la desigualdad se invierte.

A veces al resolver una desigualdad, como en el siguiente ejemplo, la variable termina sobre la derecha. Podemos reescribir la desigualdad a la inversa para obtener la variable a la izquierda.

\[x>a \text{ has the same meaning as } a<x \nonumber \]

Piénsalo como “Si Xander es más alto que Andy, entonces Andy es más bajo que Xander”.

Ejemplo$\PageIndex{7}$

Resolver cada desigualdad. Grafique la solución en la recta numérica y escriba la solución en notación de intervalos.

ⓐ$x−\frac{3}{8}\leq \frac{3}{4}$ ⓑ$9y<54$ ⓒ$−15<\frac{3}{5}z$

Responder

ⓐ

	$.$
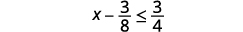
Agregar 3838 a ambos lados de la desigualdad.	$.$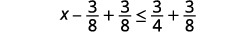
Simplificar.	$.$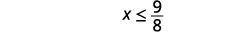
Grafique la solución en la recta numérica.	$.$
Escribe la solución en notación de intervalos.	$.$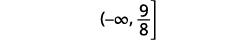

ⓑ

	$.$
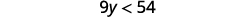
Dividir ambos lados de la desigualdad por 9; dado que 9 es positivo, la desigualdad se mantiene igual.	$.$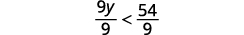
Simplificar.	$.$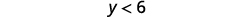
Grafique la solución en la recta numérica.	$.$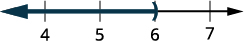
Escribe la solución en notación de intervalos.	$.$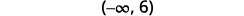

ⓒ

	$.$
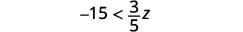
Multiplicar ambos lados de la desigualdad por$\frac{5}{3}$. Ya que$\frac{5}{3}$ es positivo, la desigualdad se mantiene igual.	$.$
Simplificar.	$.$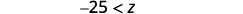
Reescribe con la variable de la izquierda.	$.$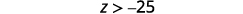
Grafique la solución en la recta numérica.	$.$
Escribe la solución en notación de intervalos.	$.$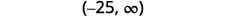

Resuelve cada desigualdad, grafica la solución en la recta numérica y escribe la solución en notación de intervalos:

ⓐ$p−\frac{3}{4}\geq \frac{1}{6}$ ⓑ$9c>72$ ⓒ$24\leq \frac{3}{8}m$

Responder

ⓐ

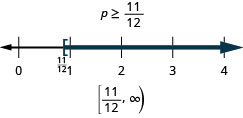
$p es menos de 11 a doceavos. La solución en la recta numérica tiene un corchete derecho en once doceavos con sombreado a la derecha. La solución en la notación de intervalos es, once doceavos hasta el infinito dentro de paréntesis y paréntesis.$

ⓑ

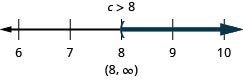
$c es menor que 8. La solución en la recta numérica tiene un corchete izquierdo en 8 con sombreado a la derecha. La solución en la notación de intervalos es, 8 a infinito entre paréntesis.$

ⓒ

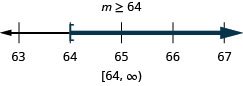
$m es mayor o igual a 8. La solución en la recta numérica tiene un corchete derecho en 64 con sombreado a la derecha. La solución en la notación de intervalos es, 64 a infinito dentro de un paréntesis y paréntesis.$

Ejemplo$\PageIndex{9}$

Resuelve cada desigualdad, grafica la solución en la recta numérica y escribe la solución en notación de intervalos:

ⓐ$r−\frac{1}{3}\leq \frac{7}{12}$ ⓑ$12d\leq 60$ ⓒ$−24<\frac{4}{3}n$

Responder

ⓐ

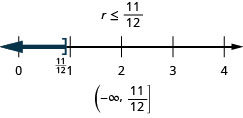
$r es menor o igual a once doceavos. La solución en la recta numérica tiene un corchete izquierdo a las once doceavos con sombreado a la izquierda. La solución en notación de intervalos es infinito negativo a once doceavos dentro de un paréntesis y un corchete.$

ⓑ

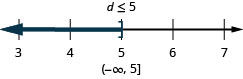
$c es menor o igual a 5. La solución en la recta numérica tiene un corchete derecho a 5 con sombreado a la izquierda. La solución en notación de intervalos es infinito negativo a 5 entre paréntesis y corchete.$

ⓒ

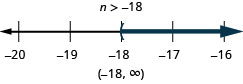
$n es mayor que negativo 18. La solución en la recta numérica tiene un paréntesis izquierdo en negativo 18 con sombreado a la derecha. La solución en la notación de intervalos es de 18 a infinito entre paréntesis.$

Tenga cuidado cuando multiplique o divida por un número negativo; recuerde revertir el signo de desigualdad.

Ejemplo$\PageIndex{10}$

Resuelve cada desigualdad, grafica la solución en la recta numérica y escribe la solución en notación de intervalos.

ⓐ$−\frac{1}{3}m\geq \frac{6}{5}$ ⓑ$\frac{n}{−2} \geq 8$

Responder

ⓐ

	$.$
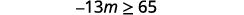
Dividir ambos lados de la desigualdad por$−\frac{1}{3}$. Ya que$−\frac{1}{3}$ es negativo, la desigualdad se invierte.	$.$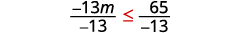
Simplificar.	$.$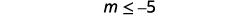
Grafique la solución en la recta numérica.	$.$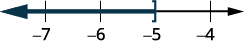
Escribe la solución en notación de intervalos.	$.$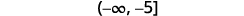

ⓑ

	$.$
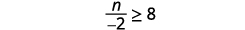
Multiplicar ambos lados de la desigualdad por$−2$. Ya que$−2$ es negativo, la desigualdad se invierte.	$.$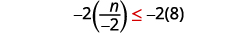
Simplificar.	$.$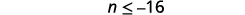
Grafique la solución en la recta numérica.	$.$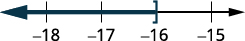
Escribe la solución en notación de intervalos.	$.$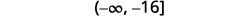

Ejemplo$\PageIndex{11}$

Resuelve cada desigualdad, grafica la solución en la recta numérica y escribe la solución en notación de intervalos:

ⓐ$−8q<32$ ⓑ$\frac{k}{−12} \leq 15$.

Responder

ⓐ

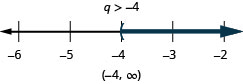
$q es mayor o igual a negativo 4. La solución en la recta numérica tiene un paréntesis izquierdo en negativo 4 con sombreado a la derecha. La solución en la notación de intervalos es de 4 a infinito entre paréntesis.$

ⓑ

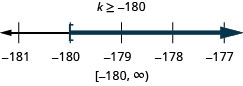
$k es mayor o igual a 180 negativo. La solución en la recta numérica tiene un corchete izquierdo en negativo 180 con sombreado a la derecha. La solución en notación de intervalos es negativa 180 a infinito dentro de un paréntesis y un paréntesis.$

Ejemplo$\PageIndex{12}$

Resuelve cada desigualdad, grafica la solución en la recta numérica y escribe la solución en notación de intervalos:

ⓐ$−7r\leq −70$ ⓑ$\frac{u}{−4}\geq −16$.

Responder

ⓐ

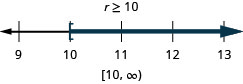
$r es mayor o igual a 10. La solución en la recta numérica tiene un corchete izquierdo a 10 con sombreado a la derecha. La solución en notación de intervalos es de 10 a infinito dentro de un paréntesis y paréntesis.$

ⓑ

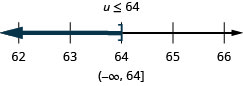
$u es menor o igual a 64. La solución en la recta numérica tiene un corchete derecho en 64 con sombreado a la izquierda. La solución en notación de intervalos es infinito negativo a 64 entre paréntesis y un corchete.$

La mayoría de las desigualdades tardarán más de un paso en resolverse. Seguimos los mismos pasos que usamos en la estrategia general para resolver ecuaciones lineales, pero asegúrate de prestar mucha atención cuando multiplicamos o dividimos para aislar la variable.

Resuelva la desigualdad$6y\leq 11y+17$, grafique la solución en la recta numérica y escriba la solución en notación de intervalos.

Responder

	$.$
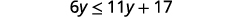
Restar 11y11y de ambos lados para recolectar las variables de la izquierda.	$.$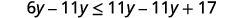
Simplificar.	$.$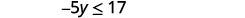
Dividir ambos lados de la desigualdad entre −5, −5 y revertir la desigualdad.	$.$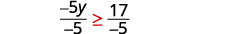
Simplificar.	$.$
Grafique la solución en la recta numérica.	$.$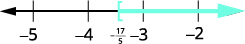
Escribe la solución en notación de intervalos.	$.$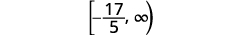

Resuelve la desigualdad, grafica la solución en la recta numérica y escribe la solución en notación de intervalos:$3q\geq 7q−23$.

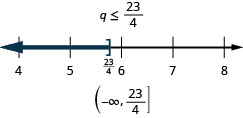
Responder: $q es menor o igual a 23 dividido por 4. La solución en la recta numérica tiene un corchete derecho en 23 dividido por 4 con sombreado a la izquierda. La solución en notación de intervalos es infinito negativo a 23 dividido por 4 dentro de un paréntesis y un paréntesis.$

Ejemplo$\PageIndex{15}$

Resuelve la desigualdad, grafica la solución en la recta numérica y escribe la solución en notación de intervalos:$6x<10x+19$.

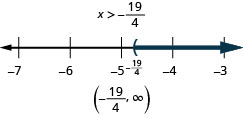
Responder: $x es mayor que negativo 19 dividido por 4. La solución en la recta numérica tiene un paréntesis izquierdo en negativo 19 dividido por 4 con sombreado a la derecha. La solución en notación de intervalos es negativa 19 dividida por 4 a infinito entre paréntesis.$

Al resolver desigualdades, suele ser más fácil recolectar las variables en el lado donde el coeficiente de la variable es mayor. Esto elimina los coeficientes negativos y así no tenemos que multiplicar o dividir por un negativo, lo que significa que no tenemos que recordar revertir el signo de desigualdad.

Ejemplo$\PageIndex{16}$

Resuelva la desigualdad$8p+3(p−12)>7p−28$, grafique la solución en la recta numérica y escriba la solución en notación de intervalos.

Responder

	$8p+3(p−12)>7p−28$
Simplifica cada lado tanto como sea posible.
Distribuir.	$8p+3p−36>7p−28$
Combina términos similares.	$11p−36>7p−28$
Restar$7p$ de ambos lados para recoger las variables de la izquierda, ya que$11>7$.	$11p−36−7p>7p−28−7p$
Simplificar.	$4p−36>−28$
Agrega$36$ a ambos lados para recoger las constantes de la derecha.	$4p−36+36>−28+36$
Simplificar.	$4p>8$
Dividir ambos lados de la desigualdad por $4$; la desigualdad permanece igual.	$\dfrac{4p}{4}>\dfrac{8}{4}$
Simplificar.	$p>2$
Grafique la solución en la recta numérica.	$.$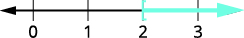
Escribe la solución en notación de intervalos.	$(2,\infty)$

Ejemplo$\PageIndex{17}$

Resuelva la desigualdad$9y+2(y+6)>5y−24$, grafique la solución en la recta numérica y escriba la solución en notación de intervalos.

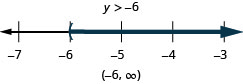
Responder: $y es mayor que negativo 6. La solución en la recta numérica tiene un paréntesis izquierdo en 6 negativo con sombreado a la derecha. La solución en la notación de intervalos es de 6 a infinito entre paréntesis.$

Ejemplo$\PageIndex{18}$

Resuelva la desigualdad$6u+8(u−1)>10u+32$, grafique la solución en la recta numérica y escriba la solución en notación de intervalos.

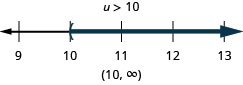
Responder: $u es mayor que negativo 10. La solución en la recta numérica tiene un paréntesis izquierdo en 10 con sombreado a la derecha. La solución en notación de intervalos es de 10 a infinito entre paréntesis.$

Así como algunas ecuaciones son identidades y otras son contradicciones, las desigualdades pueden ser identidades o contradicciones, también. Reconocemos estas formas cuando nos quedamos con solo constantes a medida que resolvemos la desigualdad. Si el resultado es una declaración verdadera, tenemos una identidad. Si el resultado es una declaración falsa, tenemos una contradicción.

Ejemplo$\PageIndex{19}$

Resuelva la desigualdad$8x−2(5−x)<4(x+9)+6x$, grafique la solución en la recta numérica y escriba la solución en notación de intervalos.

Responder

Simplifica cada lado tanto como sea posible.		$8x−2(5−x)<4(x+9)+6x$
Distribuir.		$8x−10+2x<4x+36+6x$
Combina términos similares.		$10x−10<10x+36$
Restar${\color{red}{10x}}$ de ambos lados para recoger las variables de la izquierda.		$10x−10\,{\color{red}{-\,10x}}<10x+36\,{\color{red}{-\,10x}}$
Simplificar.		$−10<36$
Los$x$'s se han ido, y tenemos una declaración verdadera.		La desigualdad es una identidad. La solución son todos los números reales.
Grafique la solución en la recta numérica.		$.$
Escribe la solución en notación de intervalos.		$(−\infty,\infty)$

Ejemplo$\PageIndex{20}$

Resuelva la desigualdad$4b−3(3−b)>5(b−6)+2b$, grafique la solución en la recta numérica y escriba la solución en notación de intervalos.

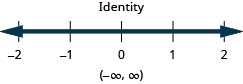
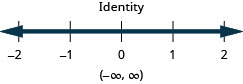
Responder: $La desigualdad es una identidad. Su solución en la recta numérica está sombreada para todos los valores. La solución en la notación de intervalos es infinito negativo a infinito entre paréntesis.$

Ejemplo$\PageIndex{21}$

Resuelva la desigualdad$9h−7(2−h)<8(h+11)+8h$, grafique la solución en la recta numérica y escriba la solución en notación de intervalos.

Responder: $La desigualdad es una identidad. Su solución en la recta numérica está sombreada para todos los valores. La solución en la notación de intervalos es infinito negativo a infinito entre paréntesis.$

Podemos borrar fracciones en desigualdades tanto como lo hicimos en ecuaciones. Nuevamente, tenga cuidado con los signos al multiplicar o dividir por un negativo.

Ejemplo$\PageIndex{22}$

Resuelva la desigualdad$\frac{1}{3}a−\frac{1}{8}a>\frac{5}{24}a+\frac{3}{4}$, grafique la solución en la recta numérica y escriba la solución en notación de intervalos.

Responder

	$\frac{1}{3}a−\frac{1}{8}a>\frac{5}{24}a+\frac{3}{4}$
Multiplica ambos lados por la LCD, 24, para borrar las fracciones.	${\color{red}{24}}\left(\dfrac{1}{3}a−\dfrac{1}{8}a\right)>\,{\color{red}{24}}\left(\dfrac{5}{24}a+\dfrac{3}{4}\right)$
Simplificar.	$ 8a - 3a > 5a + 18 $
Combina términos similares.	$ 5a > 5a + 18$
Restar$5a$ de ambos lados para recoger las variables de la izquierda.	$ 5a \,{\color{red}{-\,5a}} > 5a \,{\color{red}{-\,5a}} + 18$
Simplificar.	$0 > 18 $
El enunciado es falso.	La desigualdad es una contradicción. No hay solución.
Grafique la solución en la recta numérica.	$.$
Escribe la solución en notación de intervalos.	No hay solución.

Ejemplo$\PageIndex{23}$

Resuelva la desigualdad$\frac{1}{4}x−\frac{1}{12}x>\frac{1}{6}x+\frac{7}{8}$, grafique la solución en la recta numérica y escriba la solución en notación de intervalos.

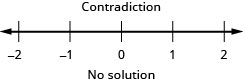
Responder: $La desigualdad es una contradicción. Entonces, no hay solución. Como resultado, no hay gráfico en la línea numérica o notación de intervalo.$

Ejemplo$\PageIndex{24}$

Resuelva la desigualdad$\frac{2}{5}z−\frac{1}{3}z<\frac{1}{15}z−\frac{3}{5}$, grafique la solución en la recta numérica y escriba la solución en notación de intervalos.

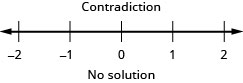
Responder: $La desigualdad es una contradicción. Entonces, no hay solución. Como resultado, no hay gráfico en la línea numérica o notación de intervalo.$

Traducir a una Desigualdad y Resolver

Para traducir frases en inglés en desigualdades, necesitamos reconocer las frases que indican la desigualdad. Algunas palabras son fáciles, como “más que” y “menos que”. Pero otros no son tan obvios. La tabla muestra algunas frases comunes que indican desigualdades.

$>$	$\geq$	$<$	$\leq$
\ (>\) ">\)” data-valign="middle” class="lt-math-17389">es mayor que es mayor que es mayor que excede	\ (\ geq\)” data-valign="middle">es mayor o igual a es al menos no es menor que es el mínimo	\ (es <\)” data-valign="middle"> menor que es menor que tiene menos que es menor que	\ (\ leq\)” data-valign="middle">es menor o igual a es como máximo no es mayor que es el máximo

Ejemplo$\PageIndex{25}$

Traducir y resolver. Luego grafica la solución en la recta numérica y escribe la solución en notación de intervalos.

\[\text{Twenty-seven less than }x\text{ is at least }48.\nonumber\]

Contestar

	$.$
Traducir.	$x - 27 \geq 48$
Solucionar: agregue 27 a ambos lados.	$ x - 27 \, {\color{red}{+\, 27}} \geq 48 \, {\color{red}{+\, 27}}$
Simplificar.	$x \geq 75$
Gráfica en la recta del número.	$.$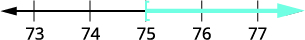
Escribir en notación de intervalos.	$[75, \infty)$

Traducir y resolver. Luego grafica la solución en la recta numérica y escribe la solución en notación de intervalos.

\[\text{Nineteen less than } p \text{ is no less than }47.\nonumber\]

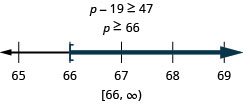
Contestar: $p menos 19 es mayor o igual a 47. Su solución es p es mayor o igual a 66. La solución en la recta numérica tiene un corchete izquierdo en 66 con sombreado a la derecha. La solución en notación de intervalos es de 66 a infinito dentro de un paréntesis y un paréntesis.$

Ejemplo$\PageIndex{27}$

Traducir y resolver. Luego grafica la solución en la recta numérica y escribe la solución en notación de intervalos.

\[\text{Four more than }a\text{ is at most }15.\nonumber\]

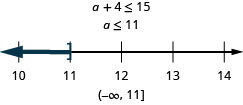
Contestar: $a más 4 es menor o igual a 15. Su solución es a es menor o igual a 11. La solución en la recta numérica tiene un corchete derecho en 11con sombreado a la izquierda. La solución en notación de intervalos es infinito negativo a 11 dentro de paréntesis y corchete.$

Resolver aplicaciones con desigualdades lineales

Muchas situaciones de la vida real requieren que resolvamos las desigualdades. El método que usaremos para resolver aplicaciones con desigualdades lineales es muy parecido al que usamos cuando resolvimos aplicaciones con ecuaciones.

Leeremos el problema y nos aseguraremos de que se entiendan todas las palabras. A continuación, identificaremos lo que estamos buscando y asignaremos una variable para representarlo. Replantearemos el problema en una frase para que sea fácil traducirlo en una desigualdad. Entonces, vamos a resolver la desigualdad.

A veces una aplicación requiere que la solución sea un número entero, pero la solución algebraica a la desigualdad no es un número entero. En ese caso, debemos redondear la solución algebraica a un número entero. El contexto de la aplicación determinará si redondeamos hacia arriba o hacia abajo.

Ejemplo$\PageIndex{28}$

Dawn ganó una mini-subvención de $4,000 para comprar computadoras tablet para su salón de clases. Las tabletas que le gustaría comprar cuestan $254.12 cada una, incluyendo impuestos y entrega. ¿Cuál es el número máximo de tabletas que Dawn puede comprar?

Contestar: \(\begin{array} {ll} {\textbf{Step 1. Read }\text{ the problem.}} &{} \\ {\textbf{Step 2. Identify }\text{what you are looking for.}} &{\text{the maximum number of tablets Dawn can buy}} \\ {\textbf{Step 3. Name}\text{ what you are looking for.}} &{} \\ {} &{} \\ {} &{\text{Let }n= \text{ the number of tablets.}} \\ {\text{Choose a variable to represent that}} &{} \\{\text{quantity.}} &{} \\ {\textbf{Step 4. Translate.}\text{Write a sentence that gives the}} &{} \\ {\text{information to find it.}} &{$254.12\text{ times the number of tablets is}} \\ {} &{\text{no more than }$4,000.} \\ {} &{\space\space\space\space\space\space\space\space\space\space\space\space 254.12n\leq 4000} \\ {\text{Translate into an inequality.}} &{} \\ {\textbf{Step 5. Solve }\text{the inequality.}} &{} \\ {} &{\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space n\leq 15.74} \\ {} &{\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space n\leq 15} \\{\text{But }n\text{ must be a whole number of}} &{} \\ {\text{tablets, so round to }15.} &{} \\ {\textbf{Step 6. Check }\text{the answer in the problem}} &{} \\ {\text{and make sure it makes sense.}} &{} \\ {} &{} \\ {} &{} \\ {\space\space\space \text{Rounding down the price to } $250, 15} &{} \\ {\space\space\space \text{tablets would cost }$3,750,\text{ while } 16} &{} \\ {\space\space\space \text{tablets would be }$4,000.\text{So a}} &{} \\ {\space\space\space \text{maximum of 15 tablets at }$254.12} &{} \\ {\space\space\space \text{seems reasonable.}} &{} \\ {\textbf{Step 7. Answer }\text{the question with a complete sentence.}} &{\text{Dawn can buy a maximum of 15 tablets.}} \\ \end{array}\)

Ejemplo$\PageIndex{29}$

Angie tiene $20 para gastar en cajas de jugo para el picnic preescolar de su hijo. Cada paquete de cajas de jugo cuesta $2.63. ¿Cuál es el número máximo de paquetes que puede comprar?

Contestar: Angie puede comprar 7 paquetes de jugo.

Ejemplo$\PageIndex{30}$

Daniel quiere sorprender a su novia con una fiesta de cumpleaños en su restaurante favorito. Tendrá un costo de $42.75 por persona para la cena, incluyendo propina e impuestos. Su presupuesto para el partido es de 500 dólares. ¿Cuál es el número máximo de personas que Daniel puede tener en la fiesta?

Contestar: Daniel puede tener 11 personas en la fiesta.

Ejemplo$\PageIndex{31}$

El plan telefónico de Taleisha le cuesta 28.80 dólares mensuales más $0.20 por mensaje de texto. ¿Cuántos mensajes de texto puede enviar/recibir y mantener su factura telefónica mensual no más de $50?

Contestar: \(\begin{array} {ll} {\textbf{Step 1. Read }\text{the problem.}} &{} \\ {\textbf{Step 2. Identify }\text{what you are looking for.}} &{\text{the number of text messages Taleisha can make}} \\ {\textbf{Step 3. Name }\text{what you are looking for.}} &{} \\ {} &{} \\ {} &{\text{Let }t= \text{the number of text messages.}} \\ {\text{Choose a variable to represent that}} &{} \\ {\text{quantity.}} &{} \\ {\textbf{Step 4. Translate }\text{Write a sentence that}} &{} \\ {\text{gives the information to find it.}} &{$28.80\text{ plus }$0.20\text{ times the number of}} \\ {} &{\text{text messages is less than or equal to }$50.} \\ {} &{28.80+0.20t \leq 50} \\ {\space\space\space \text{Translate into an inequality.}} &{} \\ {\textbf{Step 5. Solve }\text{the inequality.}} &{} \\ {} &{\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space 0.2t\leq 21.2} \\ {} &{\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space t\leq 106\text{ text messages}} \\ {} &{} \\ {\textbf{Step 6. Check }\text{the answer in the problem}} &{} \\ {\text{and make sure it makes sense.}} &{} \\ {} &{} \\ {} &{} \\{\space\space\space \text{Yes, }28.80+0.20(106)=50.} &{} \\ {\textbf{Step 7. Write }\text{a sentence that answers the question.}} &{} \\ {} &{\text{Taleisha can send/receive no more than}} \\ {} &{106\text{ text messages to keep her bill no}} \\ {} &{\text{more than } $50.} \\ \end{array}\)

Ejemplo$\PageIndex{32}$

Sergio y Lizeth tienen un presupuesto vacacional muy ajustado. Planean rentar un auto de una compañía que cobra 75 dólares a la semana más $0.25 la milla. ¿Cuántas millas pueden recorrer durante la semana y aún mantenerse dentro de su presupuesto de $200?

Contestar: Sergio y Lizeth no pueden recorrer más de 500 millas.

Ejemplo$\PageIndex{33}$

La factura de calefacción de Rameen es de $5.42 mensuales más $1.08 por therm. Cuantas termas puede usar Rameen si quiere que su factura de calefacción sea un máximo de $87.50.

Contestar: La factura de calefacción de Rameen es de $5.42 mensuales más $1.08 por therm. Cuantas termas puede usar Rameen si quiere que su factura de calefacción sea un máximo de $87.50.

El beneficio es el dinero que queda cuando se han restado los costos de los ingresos. En el siguiente ejemplo, encontraremos la cantidad de trabajos que una pequeña empresaria necesita hacer cada mes para obtener cierta cantidad de ganancias.

Ejemplo$\PageIndex{34}$

Felicity tiene un negocio de caligrafía. Ella cobra $2.50 por invitación de boda. Sus gastos mensuales son de 650 dólares. ¿Cuántas invitaciones debe escribir para obtener una ganancia de al menos 2.800 dólares mensuales?

Contestar: \(\begin{array} {ll} {\textbf{Step 1. Read }\text{the problem.}} &{} \\ {\textbf{Step 2. Identify }\text{what you are looking for.}} &{\text{the number of invitations Felicity needs to write}} \\ {\textbf{Step 3. Name }\text{what you are looking for.}} &{\text{Let }j=\text{ the number of invitations.}} \\ {} &{} \\ {\space\space\space\text{Choose a variable to represent it.}} &{} \\ {\textbf{Step 4. Translate. }\text{Write a sentence that}} &{} \\ {\text{gives the information to find it.}} &{$2.50 \text{ times the number of invitations}} \\ {} &{\text{minus }$650\text{ is at least }$2,800.} \\ {} &{\space\space\space 2.50j−650\geq 2,800} \\ {\space\space\space \text{Translate into an inequality.}} &{} \\ {\textbf{Step 5. Solve }\text{the inequality.}} &{} \\ {} &{\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space 2.5j\geq 3,450} \\ {} &{\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space j\geq 1,380 \text{ invitations}} \\ {\textbf{Step 6. Check }\text{the answer in the problem}} &{} \\ {\text{and make sure it makes sense.}} &{} \\ {} &{} \\ {} &{} \\ {\space\space\space \text{If Felicity wrote }1400\text{ invitations, her}} &{} \\ {\space\space\space \text{profit would be }2.50(1400)−650, \text{or}} &{} \\ {\space\space\space $2,850.\text{ This is more than }$2800.} &{} \\ {\textbf{Step 7. Write }\text{a sentence that answers the question.}} &{\text{Felicity must write at least }1,380\text{ invitations.}} \\ \end{array}\)

Ejemplo$\PageIndex{35}$

Caleb tiene un negocio de cuidado de mascotas. Él cobra 32 dólares por hora. Sus gastos mensuales son de $2,272. ¿Cuántas horas debe trabajar para obtener una ganancia de al menos 800 dólares mensuales?

Contestar: Caleb debe trabajar al menos 96 horas.

Ejemplo$\PageIndex{36}$

Elliot tiene un negocio de mantenimiento paisajístico. Sus gastos mensuales son de $1,100. Si cobra 60 dólares por trabajo, ¿cuántos trabajos debe hacer para obtener una ganancia de al menos $4,000 mensuales?

Contestar: Elliot debe trabajar al menos 85 empleos.

Son muchas las situaciones en las que varias cantidades contribuyen al gasto total. Debemos asegurarnos de contabilizar todos los gastos individuales cuando resolvamos problemas como este.

Ejemplo$\PageIndex{37}$

Malik está planeando un viaje de vacaciones de verano de seis días. Tiene 840 dólares en ahorros, y gana 45 dólares por hora por tutoría. El viaje le costará 525 dólares por pasaje aéreo, 780 dólares por comida y turismo, y 95 dólares por noche para el hotel. ¿Cuántas horas debe ser tutor para tener el dinero suficiente para pagar el viaje?

Contestar: \(\begin{array} {ll} {} &{} \\ {\textbf{Step 1. Read }\text{the problem.}} &{} \\ {\textbf{Step 2. Identify }\text{what you are looking for.}} &{\text{the number of hours Malik must tutor}} \\ {\textbf{Step 3. Name }\text{what you are looking for.}} &{} \\ {} &{} \\ {} &{\text{Let }h=\text{ the number of hours.}} \\ {\space\space\space\space\space\space\space \text{Choose a variable to represent that}} &{} \\ {\space\space\space\space\space\space\space \text{quantity.}} &{} \\ {\textbf{Step 4. Translate. }\text{Write a sentence that}} &{} \\ {\text{gives the information to find it.}} &{} \\ {} &{\text{The expenses must be less than or equal to}} \\{} &{\text{the income. The cost of airfare plus the}} \\{} &{\text{cost of food and sightseeing and the hotel}} \\{} &{\text{bill must be less than the savings plus the}} \\{} &{\text{amount earned tutoring.}} \\{} &{} \\ {} &{} \\ {} &{} \\ {} &{} \\ {\space\space\space\space\space\space\space \text{Translate into an inequality.}} &{525+780+95(6)\leq 840+45h} \\ {\textbf{Step 5. Solve }\text{the inequality.}} &{} \\ {} &{} \\ {} &{\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space 1,875\leq 840+45h} \\ {} &{\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space 1,035\leq 45h} \\ {} &{\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space 23\leq h} \\ {} &{\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space h\geq 23} \\ {} &{} \\ {} &{} \\ {\textbf{Step 6. Check }\text{the answer in the problem}} &{} \\ {\text{and make sure it makes sense.}} &{} \\ {\text{We substitute 23 into the inequality.}} &{} \\ {} &{} \\ {} &{} \\ {\space\space\space\space\space\space\space\space 1,875\leq 840+45h} &{} \\ {\space\space\space\space\space\space\space\space 1,875\leq 840+45(23)} &{} \\ {\space\space\space\space\space\space\space\space 1,875\leq 1875} &{} \\ {\textbf{Step 7. Write }\text{a sentence that answers the question.}} &{\text{Malik must tutor at least }23\text{ hours.}} \\ \end{array}\)

Ejemplo$\PageIndex{38}$

La mejor amiga de Brenda está teniendo una boda de destino y el evento durará tres días. Brenda tiene $500 en ahorros y puede ganar $15 la hora de niñera. Ella espera pagar $350 pasajes aéreos, $375 por comida y entretenimiento y $60 la noche por su parte de una habitación de hotel. ¿Cuántas horas debe cuidar de niños para tener suficiente dinero para pagar el viaje?

Contestar: Brenda debe tener cuidado de niños por lo menos 27 horas.

Ejemplo$\PageIndex{39}$

Josue quiere hacer un viaje por carretera de 10 noches con amigos la próxima primavera. Le costará 180 dólares por gasolina, 450 dólares por comida y 49 dólares por noche compartir una habitación de motel. Tiene $520 en ahorros y puede ganar $30 por camino de entrada paleando nieve. ¿Cuántas entradas debe palear para tener suficiente dinero para pagar el viaje?

Contestar: Josue debe palear al menos 20 calzadas.

Conceptos clave

Desigualdades, líneas numéricas y notación de intervalos
$x>a \quad x\geq a\quad x<a\quad x\leq a$
$La figura muestra que la solución de la desigualdad x es mayor que a se indica en una recta numérica con un paréntesis izquierdo en a y sombreado a la derecha, y que la solución en notación de intervalo es el intervalo de a a infinito encerrado entre paréntesis. Se muestra que la solución de la desigualdad x es mayor o igual que a se indica en una recta numérica con un paréntesis izquierdo en a y sombreado a la derecha, y que la solución en notación de intervalo es el intervalo a al infinito dentro de un paréntesis izquierdo y paréntesis derecho. Se muestra que la solución de la desigualdad x es menor que a se indica en una recta numérica con un paréntesis derecho en a y sombreado a la izquierda, y que la solución en notación de intervalo es el intervalo infinito negativo a a entre paréntesis. Se muestra que la solución de la desigualdad x es menor o igual a a se indica en la línea anumber con un corchetes derecho en a y sombreado a la izquierda, y que la solución en notación de intervalo es infinito negativo a a dentro de un paréntesis izquierdo y corchetes derecho.$
Desigualdad Lineal
- Una desigualdad lineal es una desigualdad en una variable que se puede escribir en una de las siguientes formas donde a, b y c son números reales y$a\neq 0$:
  \[ax+b<c, \qquad ax+b\leq c, \qquad ax+b>c, \qquad ax+b\geq c.\nonumber\]
Propiedad de Suma y Resta de Desigualdad
- Para cualquier número a, b y c, si a<b, entoncesa<b, entonces
  \[\begin{array} {ll} {a+c<b+c} &{a−c<b−c} \\ {a+c>b+c} &{a−c>b−c} \\ \end{array} \nonumber\]
- Podemos sumar o restar la misma cantidad de ambos lados de una desigualdad y aún así mantener la desigualdad.
Multiplicación y División Propiedad de Desigualdad
- Para cualquier número a, b y c,
  $\begin{array} {l} \text{multiply or divide by a }\textbf{positive} \\ \\ \space\space\space\space\space\space\space\text{if }a<b\text{ and }c>0,\text{ then } ac<bc\text{ and }\frac{a}{c}<\frac{b}{c}. \\ \space\space\space\space\space\space\space\text{if }a>b\text{ and }c>0,\text{ then } ac>bc\text{ and }\frac{a}{c}>\frac{b}{c}. \\ \text{multiply or divide by a }\textbf{negative} \\ \\ \space\space\space\space\space\space\space\text{if }a<b\text{ and }c<0,\text{ then } ac>bc\text{ and }\frac{a}{c}>\frac{b}{c}. \\ \space\space\space\space\space\space\space\text{if }a>b\text{ and }c<0,\text{ then } ac<bc\text{ and }\frac{a}{c}<\frac{b}{c}. \\ \end{array}$

Frases que indican desigualdades

$>$	$\geq$	$<$	$\leq$
\ (>\) ">es mayor que es mayor que es mayor que excede	\ (\ geq\)” data-valign="middle">es mayor o igual a es al menos no es menor que es el mínimo	\ (es <\)” data-valign="middle"> menor que es menor que tiene menos que es menor que	\ (\ leq\)” data-valign="middle">es menor o igual a es como máximo no es mayor que es el máximo

	\( x \geq -3 \)
Sombra a la derecha de\(−3\), y coloque un soporte en\(−3\).	$.$
Escribir en notación de intervalos.	\( [-3, \infty) \)

	\( x \leq -\dfrac{3}{5} \)
Sombra a la izquierda de\(−\frac{3}{5}\), y poner un soporte en\(−\frac{3}{5}\).	$.$
Escribir en notación de intervalos.	\( \bigg( -\infty, \dfrac{3}{5}\bigg] \)

		\(-3 < x < 4\)
Sombra entre\(−3\) y 4. Poner paréntesis en\(−3\) y 4.		$.$
Escribir en notación de intervalos.		\( (-3,4) \)

			\( -6 \leq x < -1 \)
Sombra entre\(−6\) y −1. Ponga un corchete en\(−6\), y un paréntesis en −1.			$.$
Escribir en notación de intervalos.			\( [-6,1) \)

	\(8p+3(p−12)>7p−28\)
Simplifica cada lado tanto como sea posible.
Distribuir.	\(8p+3p−36>7p−28\)
Combina términos similares.	\(11p−36>7p−28\)
Restar\(7p\) de ambos lados para recoger las variables de la izquierda, ya que\(11>7\).	\(11p−36−7p>7p−28−7p\)
Simplificar.	\(4p−36>−28\)
Agrega\(36\) a ambos lados para recoger las constantes de la derecha.	\(4p−36+36>−28+36\)
Simplificar.	\(4p>8\)
Dividir ambos lados de la desigualdad por \(4\); la desigualdad permanece igual.	\(\dfrac{4p}{4}>\dfrac{8}{4}\)
Simplificar.	\(p>2\)
Grafique la solución en la recta numérica.	$.$
Escribe la solución en notación de intervalos.	\((2,\infty)\)

Search

Desigualdades, líneas numéricas y notación de intervalos

Ejemplo\(\PageIndex{1}\)

Ejemplo\(\PageIndex{3}\)

Ejemplo\(\PageIndex{5}\)

Ejemplo\(\PageIndex{6}\)

Desigualdad lineal

Suma y resta propiedad de desigualdad

Multiplicación y división de propiedad de la desigualdad

Ejemplo\(\PageIndex{7}\)

Ejemplo\(\PageIndex{9}\)

Ejemplo\(\PageIndex{10}\)

Ejemplo\(\PageIndex{11}\)

Ejemplo\(\PageIndex{12}\)

Ejemplo\(\PageIndex{15}\)

Ejemplo\(\PageIndex{16}\)

Ejemplo\(\PageIndex{17}\)

Ejemplo\(\PageIndex{18}\)

Ejemplo\(\PageIndex{19}\)

Ejemplo\(\PageIndex{20}\)

Ejemplo\(\PageIndex{21}\)

Ejemplo\(\PageIndex{22}\)

Ejemplo\(\PageIndex{23}\)

Ejemplo\(\PageIndex{24}\)

Ejemplo\(\PageIndex{25}\)

Ejemplo\(\PageIndex{27}\)

Ejemplo\(\PageIndex{28}\)

Ejemplo\(\PageIndex{29}\)

Ejemplo\(\PageIndex{30}\)

Ejemplo\(\PageIndex{31}\)

Ejemplo\(\PageIndex{32}\)

Ejemplo\(\PageIndex{33}\)

Ejemplo\(\PageIndex{34}\)

Ejemplo\(\PageIndex{35}\)

Ejemplo\(\PageIndex{36}\)

Ejemplo\(\PageIndex{37}\)

Ejemplo\(\PageIndex{38}\)

Ejemplo\(\PageIndex{39}\)

	\( x < 2.5 \)
Sombra a la izquierda de 2.5 y ponga un paréntesis en 2.5.	$.$
Escribir en notación de intervalos.	\( (-\infty, 2.5) \)

			\( 0 \leq x \leq 2.5 \)
Sombra entre 0 y 2.5. Poner un soporte en 0 y en 2.5.			$.$
Escribir en notación de intervalos.			\( [0, 2.5] \)

Simplifica cada lado tanto como sea posible.		\(8x−2(5−x)<4(x+9)+6x\)
Distribuir.		\(8x−10+2x<4x+36+6x\)
Combina términos similares.		\(10x−10<10x+36\)
Restar\({\color{red}{10x}}\) de ambos lados para recoger las variables de la izquierda.		\(10x−10\,{\color{red}{-\,10x}}<10x+36\,{\color{red}{-\,10x}}\)
Simplificar.		\(−10<36\)
Los\(x\)'s se han ido, y tenemos una declaración verdadera.		La desigualdad es una identidad. La solución son todos los números reales.
Grafique la solución en la recta numérica.		$.$
Escribe la solución en notación de intervalos.		\((−\infty,\infty)\)

	\(\frac{1}{3}a−\frac{1}{8}a>\frac{5}{24}a+\frac{3}{4}\)
Multiplica ambos lados por la LCD, 24, para borrar las fracciones.	\({\color{red}{24}}\left(\dfrac{1}{3}a−\dfrac{1}{8}a\right)>\,{\color{red}{24}}\left(\dfrac{5}{24}a+\dfrac{3}{4}\right)\)
Simplificar.	\( 8a - 3a > 5a + 18 \)
Combina términos similares.	\( 5a > 5a + 18\)
Restar\(5a\) de ambos lados para recoger las variables de la izquierda.	\( 5a \,{\color{red}{-\,5a}} > 5a \,{\color{red}{-\,5a}} + 18\)
Simplificar.	\(0 > 18 \)
El enunciado es falso.	La desigualdad es una contradicción. No hay solución.
Grafique la solución en la recta numérica.	$.$
Escribe la solución en notación de intervalos.	No hay solución.

	$.$
Traducir.	\(x - 27 \geq 48\)
Solucionar: agregue 27 a ambos lados.	\( x - 27 \, {\color{red}{+\, 27}} \geq 48 \, {\color{red}{+\, 27}}\)
Simplificar.	\(x \geq 75\)
Gráfica en la recta del número.	$.$
Escribir en notación de intervalos.	\([75, \infty)\)