Capítulo 3 Ejercicios de revisión

Última actualización
Guardar como PDF

Page ID: 112250

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Ejercicios de revisión de capítulos

Gráfica ecuaciones lineales en dos variables

Trazar puntos en un sistema de coordenadas rectangulares

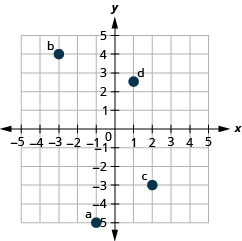
En los siguientes ejercicios, trazar cada punto en un sistema de coordenadas rectangulares.

1. ⓐ$(−1,−5)$
ⓑ$(−3,4)$
ⓒ$(2,−3)$
ⓓ$(1,\frac{5}{2})$

Contestar: $Esta figura muestra los puntos trazados en el plano de la coordenada x y. Los ejes x e y van de 5 a 5 negativos. El punto etiquetado a es de 1 unidades a la izquierda del origen y 5 unidades por debajo del origen y se ubica en el cuadrante III. El punto etiquetado b está a 3 unidades a la izquierda del origen y 4 unidades por encima del origen y se ubica en el cuadrante II. El punto etiquetado c es de 2 unidades a la derecha del origen y 3 unidades por debajo del origen y se ubica en el cuadrante IV. El punto etiquetado d es 1 unidad a la derecha del origen y 2.5 unidades por encima del origen y se ubica en el cuadrante I.$

2. ⓐ$(−2,0)$
ⓑ$(0,−4)$
ⓒ$(0,5)$
ⓓ$(3,0)$

En los siguientes ejercicios, determinar qué pares ordenados son soluciones a las ecuaciones dadas.

3. $5x+y=10$;

ⓐ$(5,1)$
ⓑ$(2,0)$
ⓒ$(4,−10)$

Contestar: ⓑ, ⓒ

4. $y=6x−2$;

ⓐ$(1,4)$
ⓑ$(13,0)$
ⓒ$(6,−2)$

Graficar una ecuación lineal trazando puntos

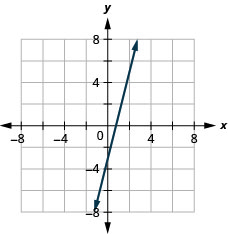
En los siguientes ejercicios, grafica por puntos de trazado.

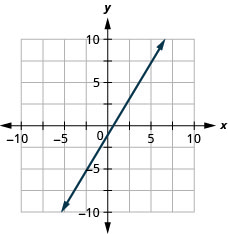
5. $y=4x−3$

Contestar: $Esta figura muestra una línea recta graficada en el plano de la coordenada x y. Los ejes x e y van de negativo 8 a 8. La línea pasa por los puntos (negativo 1, negativo 7), (0, negativo 3), (1, negativo 1) y (2, 3).$

6. $y=−3x$

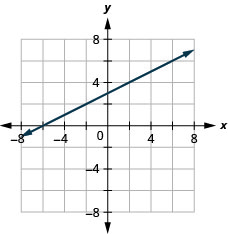
7. $y=\frac{1}{2}x+3$

Contestar: $Esta figura muestra una línea recta graficada en el plano de la coordenada x y. Los ejes x e y van de negativo 8 a 8. La línea pasa por los puntos (negativo 6, 0), (0, 3), (2, 4) y (4, 5).$

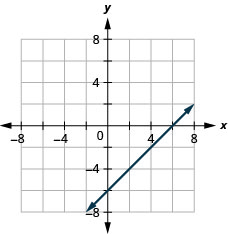
8. $y=−\frac{4}{5}|x−1$

9. $x−y=6$

Contestar: $Esta figura muestra una línea recta graficada en el plano de la coordenada x y. Los ejes x e y van de negativo 8 a 8. La línea pasa por los puntos (negativo 1, negativo 7), (0, negativo 6), (3, negativo 3) y (6, 0).$

10. $2x+y=7$

11. $3x−2y=6$

Contestar: $Esta figura muestra una línea recta graficada en el plano de la coordenada x y. Los ejes x e y van de negativo 8 a 8. La línea pasa por los puntos (negativo 2, negativo 6), (0, negativo 3), (2, 0) y (4, 3).$

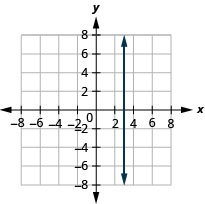
Gráfica líneas verticales y horizontales

En los siguientes ejercicios, grafica cada ecuación.

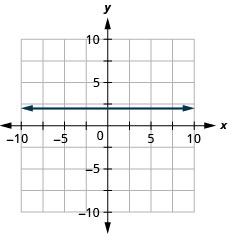
12. $y=−2$

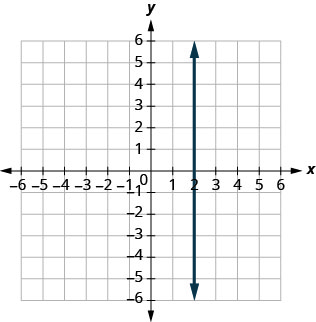
13. $x=3$

Contestar: $Esta figura muestra una línea recta vertical graficada en el plano de la coordenada x y. Los ejes x e y van de negativo 8 a 8. La línea pasa por los puntos (3, negativo 1), (3, 0) y (3, 1).$

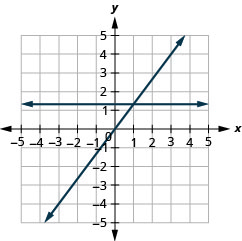
En los siguientes ejercicios, grafica cada par de ecuaciones en un mismo sistema de coordenadas rectangulares.

14. $y=−2x$y$y=−2$

15. $y=\frac{4}{3}x$y$y=\frac{4}{3}$

Contestar: $La figura muestra las gráficas de una línea recta horizontal y una línea recta inclinada en el mismo plano de coordenadas x y. Los ejes x e y van de 5 a 5 negativos. La línea horizontal pasa por los puntos (0, 4 dividido por 3), (1, 4 dividido por 3), y (2, 4 dividido por 3). La línea inclinada pasa por los puntos (0, 0), (1, 4 dividido por 3), y (2, 8 dividido por 3).$

Buscar intercepciones x e y

En los siguientes ejercicios, encuentra las intercepciones x - e y.

16.
$La figura muestra una línea recta graficada en el plano de la coordenada x y. Los ejes x e y van de negativo 8 a 8. La línea pasa por los puntos (negativo 6, negativo 2), (negativo 4, 0), (negativo 2, 2), (0, 4), (2, 6) y (4, 8).$

17.
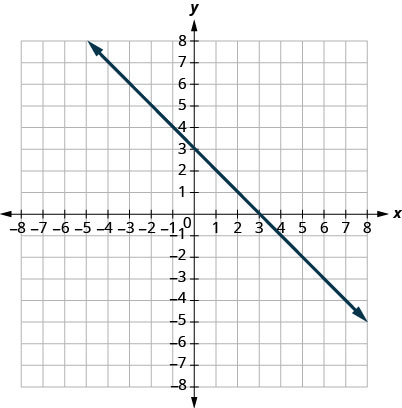
$La figura muestra una línea recta graficada en el plano de la coordenada x y. Los ejes x e y van de negativo 8 a 8. La línea pasa por los puntos (negativo 2, 5), (negativo 1, 4), (0, 3), (3, 0) y (6, negativo 3).$

Contestar: $(0,3)(3,0)$

En los siguientes ejercicios, encuentra las intercepciones de cada ecuación.

18. $x−y=−1$

19. $x+2y=6$

Contestar: $(6,0),\space (0,3)$

20. $2x+3y=12$

21. $y=\frac{3}{4}x−12$

Contestar: $(16,0),\space (0,−12)$

22. $y=3x$

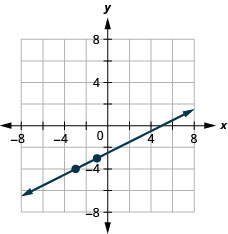
Graficar una línea usando las intercepciones

En los siguientes ejercicios, grafica usando las intercepciones.

23. $−x+3y=3$

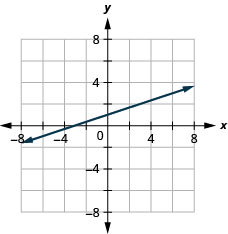
Contestar: $La figura muestra una línea recta graficada en el plano de la coordenada x y. Los ejes x e y van de negativo 8 a 8. La línea pasa por los puntos (negativo 3, 0), (0, 1), (3, 2) y (6, 3).$

24. $x−y=4$

25. $2x−y=5$

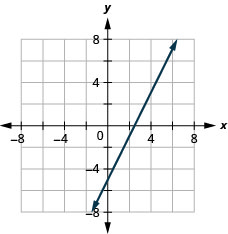
Contestar: $La figura muestra una línea recta graficada en el plano de la coordenada x y. Los ejes x e y van de negativo 8 a 8. La línea pasa por los puntos (0, negativo 5), (1, negativo 3), (2, negativo 1) y (3, 1).$

26. $2x−4y=8$

27. $y=4x$

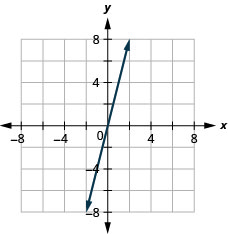
Contestar: $La figura muestra una línea recta graficada en el plano de la coordenada x y. Los ejes x e y van de negativo 8 a 8. La línea pasa por los puntos (negativo 1, 4), (0, 0) y (1, negativo 4).$

Pendiente de una Línea

Encuentra la pendiente de una línea

En los siguientes ejercicios, encuentra la pendiente de cada línea mostrada.

28.
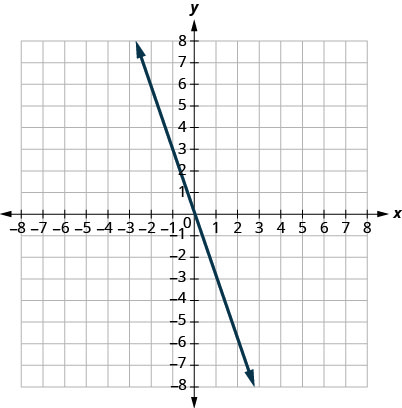
$Esta figura muestra la gráfica de una línea recta en el plano de la coordenada x y. El eje x va desde el 6 negativo hasta el 6. El eje y va de 6 a 6 negativos. La línea pasa por los puntos (0, 0) y (1, negativo 3).$

29.
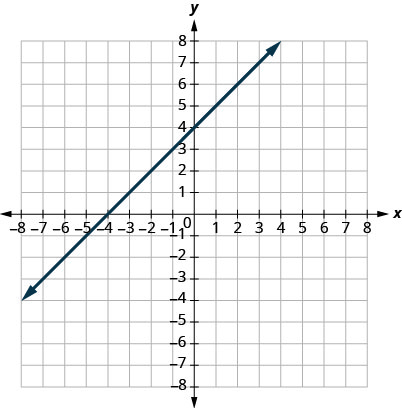
$Esta figura muestra la gráfica de una línea recta en el plano de la coordenada x y. El eje x va desde el 6 negativo hasta el 6. El eje y va de 6 a 6 negativos. La línea pasa por los puntos (negativo 4, 0) y (0, 4).$

Contestar: 1

30.
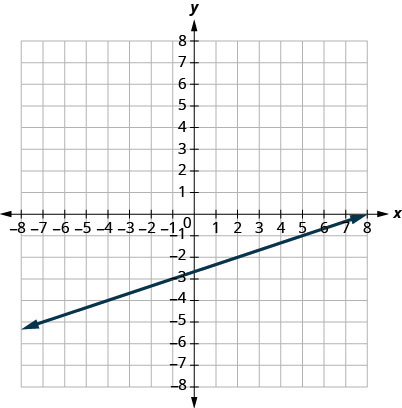
$Esta figura muestra la gráfica de una línea recta en el plano de la coordenada x y. El eje x va desde el 6 negativo hasta el 6. El eje y va de 6 a 6 negativos. La línea pasa por los puntos (negativo 4, negativo 4) y (2, negativo 2).$

31.
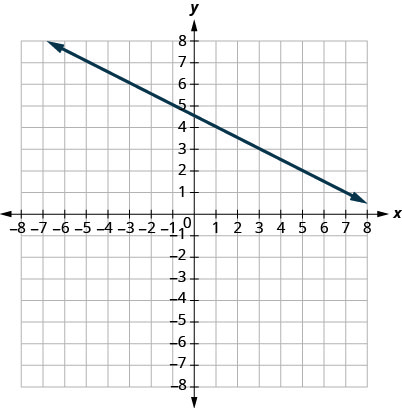
$Esta figura muestra la gráfica de una línea recta en el plano de la coordenada x y. El eje x va desde el 6 negativo hasta el 6. El eje y va de 6 a 6 negativos. La línea pasa por los puntos (1, 4) y (5, 2).$

Contestar: $−12$

En los siguientes ejercicios, encuentra la pendiente de cada línea.

32. $y=2$

33. $x=5$

Contestar: undefined

34. $x=−3$

35. $y=−1$

Contestar: 0

Usa la Fórmula de Talud para encontrar la Talud de una Línea entre Dos Puntos

En los siguientes ejercicios, usa la fórmula de pendiente para encontrar la pendiente de la línea entre cada par de puntos.

36. $(−1,−1),(0,5)$

37. $(3.5),(4,−1)$

Contestar: $−6$

38. $(−5,−2),(3,2)$

39. $(2,1),(4,6)$

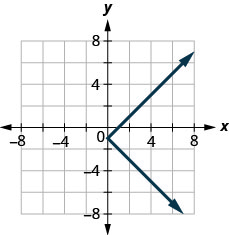
Contestar: $52$

Graficar una línea dado un punto y el talud

En los siguientes ejercicios, grafica cada línea con el punto y pendiente dados.

40. $(2,−2);\space m=52$

41. $(−3,4);\space m=−13$

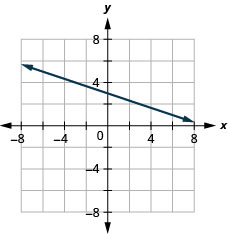
Contestar: $Esta figura muestra la gráfica de una línea recta en el plano de la coordenada x y. El eje x va de negativo 8 a 8. El eje y va de negativo 8 a 8. La línea pasa por los puntos (negativo 3, 4) y (0, 3).$

42. $x$-interceptar$−4; m=3$

43. $y$-interceptar$1; m=−34$

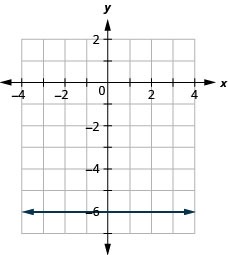
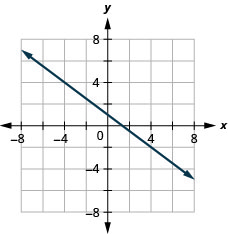
Contestar: $Esta figura muestra la gráfica de una línea recta en el plano de la coordenada x y. El eje x va de negativo 8 a 8. El eje y va de negativo 8 a 8. La línea pasa por los puntos (0, 1) y (4, negativo 2).$

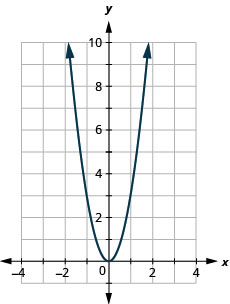
Graficar una línea usando su pendiente e intercepción

En los siguientes ejercicios, identificar la pendiente e$y$ -intercepción de cada línea.

44. $y=−4x+9$

45. $y=53x−6$

Contestar: $m=53;\space (0,−6)$

46. $5x+y=10$

47. $4x−5y=8$

Contestar: $m=\frac{4}{5};\space (0,−\frac{8}{5})$

En los siguientes ejercicios, grafica la línea de cada ecuación usando su pendiente y -intercepción.

48. $y=2x+3$

49. $y=−x−1$

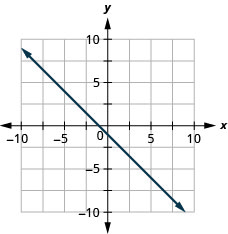
Contestar: $Esta figura muestra la gráfica de una línea recta en el plano de la coordenada x y. El eje x va de negativo 10 a 10. El eje y va de negativo 10 a 10. La línea pasa por los puntos (0, negativo 1) y (1, negativo 2).$

50. $y=−25x+3$

51. $4x−3y=12$

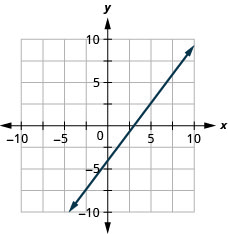
Contestar: $Esta figura muestra la gráfica de una línea recta en el plano de la coordenada x y. El eje x va de negativo 10 a 10. El eje y va de negativo 10 a 10. La línea pasa por los puntos (0, negativo 4) y (3, 0).$

En los siguientes ejercicios, determine el método más conveniente para graficar cada línea.

52. $x=5$

53. $y=−3$

Contestar: línea horizontal

54. $2x+y=5$

55. $x−y=2$

Contestar: intercepta

56. $y=22x+2$

57. $y=34x−1$

Contestar: trazando puntos

Gráfica e Interpreta Aplicaciones de Inclinación-Intercepción

58. Katherine es chef privada. La ecuación$C=6.5m+42$ modela la relación entre su costo semanal, C, en dólares y el número de comidas, m, que sirve.

ⓐ Encuentra el costo de Katherine por una semana cuando no sirve comidas.
ⓑ Encuentra el costo por una semana cuando sirve 14 comidas.
ⓒ Interpretar la pendiente y C -intercepción de la ecuación.
ⓓ Grafica la ecuación.

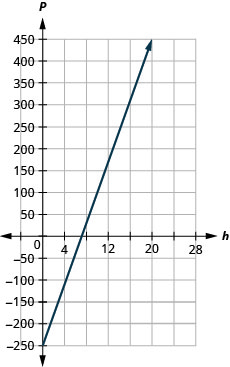
59. Marjorie enseña piano. La ecuación$P=35h−250$ modela la relación entre su ganancia semanal, P, en dólares y el número de lecciones estudiantiles, s, que imparte.

ⓐ Encuentra las ganancias de Marjorie durante una semana cuando no da clases de alumnos.
ⓑ Encuentra la ganancia para una semana cuando imparte 20 clases de alumnos.
ⓒ Interpretar la pendiente y P -intercepción de la ecuación.
ⓓ Grafica la ecuación.

Contestar

ⓐ$−$250$
ⓑ$$450$
ⓒ La pendiente, 35, significa que la ganancia semanal de Marjorie, P, aumenta en 35 dólares por cada lección adicional de estudiante que imparte.
El P -intercepto significa que cuando el número de lecciones es 0, Marjorie pierde 250 dólares.
ⓓ

$Esta figura muestra la gráfica de una línea recta en el plano de la coordenada x y. El eje x va de negativo 4 a 28. El eje y va de 250 negativos a 450. La línea pasa por los puntos (0, negativo 250) y (20, 450).$

Utilizar pendientes para identificar líneas paralelas y perpendiculares

En los siguientes ejercicios, use pendientes e$y$ intercepciones para determinar si las líneas son paralelas, perpendiculares o ninguna.

60. $4x−3y=−1;\quad y=43x−3$

61. $y=5x−1;\quad 10x+2y=0$

Contestar: ni

62. $3x−2y=5;\quad 2x+3y=6$

63. $2x−y=8;\quad x−2y=4$

Contestar: no paralelo

Encuentra la ecuación de una línea

Encontrar una ecuación de la línea dada la pendiente y la intersección y

En los siguientes ejercicios, encuentra la ecuación de una línea con pendiente dada e intersección en y. Escribe la ecuación en forma de pendiente-intercepción.

64. Pendiente$\frac{1}{3}$ e$y$ intercepción$(0,−6)$

65. Pendiente$−5$ e$y$ intercepción$(0,−3)$

Contestar: $y=−5x−3$

66. Pendiente$0$ e$y$ intercepción$(0,4)$

67. Pendiente$−2$ e$y$ intercepción$(0,0)$

Contestar: $y=−2x$

En los siguientes ejercicios, encuentra la ecuación de la línea que se muestra en cada gráfica. Escribe la ecuación en forma de pendiente-intercepción.

68.
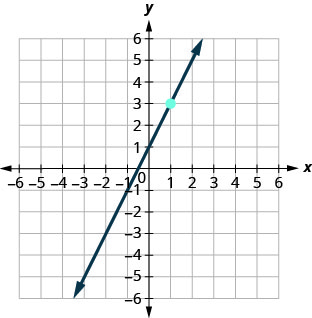
$Esta figura tiene una gráfica de una línea recta en el plano de la coordenada x y. Los ejes x e y van de negativo 10 a 10. La línea pasa por los puntos (0, 1), (1, 3) y (2, 5).$

69.
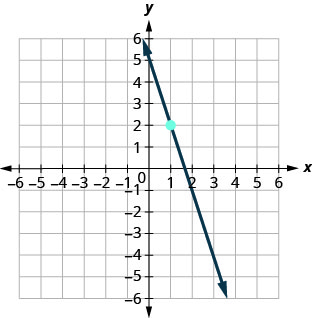
$Esta figura tiene una gráfica de una línea recta en el plano de la coordenada x y. Los ejes x e y van de negativo 10 a 10. La línea pasa por los puntos (0, 5), (1, 2) y (2, negativo 1).$

Contestar: $y=−3x+5$

70.
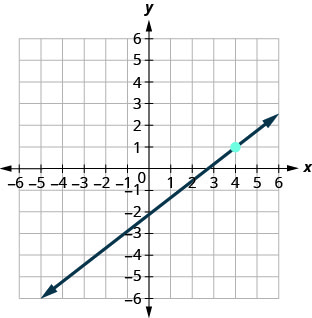
$Esta figura tiene una gráfica de una línea recta en el plano de la coordenada x y. Los ejes x e y van de negativo 10 a 10. La línea pasa por los puntos (0, negativo 2), (4, 1) y (8, 4).$

71.
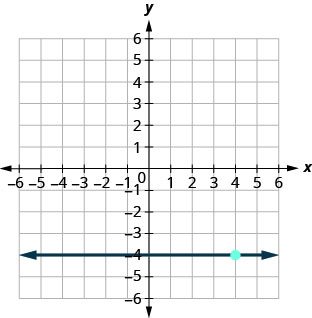
$Esta figura tiene una gráfica de una línea recta horizontal en el plano de la coordenada x y. Los ejes x e y van de negativo 10 a 10. La línea pasa por los puntos (0, negativo 4), (1, negativo 4) y (2, negativo 4).$

Contestar: $y=−4$

Encontrar una ecuación de la línea dada la pendiente y un punto

En los siguientes ejercicios, encuentra la ecuación de una línea con pendiente dada y que contiene el punto dado. Escribe la ecuación en forma de pendiente-intercepción.

72. $m=−\frac{1}{4}$, punto$(−8,3)$

73. $m=\frac{3}{5}$, punto$(10,6)$

Contestar: $y=\frac{3}{5}x$

74. Línea horizontal que contiene$(−2,7)$

75. $m=−2$, punto$(−1,−3)$

Contestar: $y=−2x−5$

Encontrar una ecuación de la línea dada dos puntos

En los siguientes ejercicios, encuentra la ecuación de una línea que contiene los puntos dados. Escribe la ecuación en forma de pendiente-intercepción.

76. $(2,10)$y$(−2,−2)$

77. $(7,1)$y$(5,0)$

Contestar: $y=\frac{1}{2}x−\frac{5}{2}$

78. $(3,8)$y$(3,−4)$

79. $(5,2)$y$(−1,2)$

Contestar: $y=2$

Encontrar una ecuación de una línea paralela a una línea dada

En los siguientes ejercicios, encuentra una ecuación de una línea paralela a la línea dada y contiene el punto dado. Escribe la ecuación en forma de pendiente-intercepción.

80. línea$y=−3x+6$, punto$(1,−5)$

81. línea$2x+5y=−10$, punto$(10,4)$

Contestar: $y=−\frac{2}{5}x+8$

82. línea$x=4$, punto$(−2,−1)$

83. línea$y=−5$, punto$(−4,3)$

Contestar: $y=3$

Encontrar una ecuación de una línea perpendicular a una línea dada

En los siguientes ejercicios, encuentra una ecuación de una línea perpendicular a la línea dada y contiene el punto dado. Escribe la ecuación en forma de pendiente-intercepción.

84. línea$y=−\frac{4}{5}x+2$, punto$(8,9)$

85. línea$2x−3y=9$, punto$(−4,0)$

Contestar: $y=−\frac{3}{2}x−6$

86. línea$y=3$, punto$(−1,−3)$

87.$x=−5$ punto de línea$(2,1)$

Contestar: $y=1$

Graficar desigualdades lineales en dos variables

Verificar soluciones a una desigualdad en dos variables

En los siguientes ejercicios, determinar si cada par ordenado es una solución a la desigualdad dada.

88. Determine si cada par ordenado es una solución a la desigualdad$y<x−3$:

ⓐ$(0,1)$ ⓑ$(−2,−4)$ ⓒ$(5,2)$ ⓓ$(3,−1)$
ⓔ$(−1,−5)$

89. Determine si cada par ordenado es una solución a la desigualdad$x+y>4$:

ⓐ$(6,1)$ ⓑ$(−3,6)$ ⓒ$(3,2)$ ⓓ$(−5,10)$ ⓔ$(0,0)$

Contestar: ⓐ si ⓑ no ⓒ si ⓓ si; ⓔ nom

Reconocer la relación entre las soluciones de una desigualdad y su gráfica

En los siguientes ejercicios, escriba la desigualdad mostrada por la región sombreada.

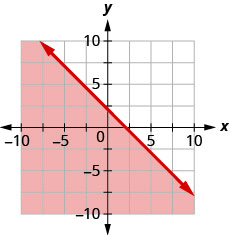
90. Escribe la desigualdad que muestra la gráfica con la línea límite$y=−x+2.$

$Esta figura tiene la gráfica de una línea recta en el plano de la coordenada x y. Los ejes x e y van de negativo 10 a 10. Se dibuja una línea a través de los puntos (0, 2), (1, 1) y (2, 0). La línea divide el plano de la coordenada x y en dos mitades. La línea y la mitad inferior izquierda están sombreadas en rojo para indicar que aquí es donde están las soluciones de la desigualdad.$

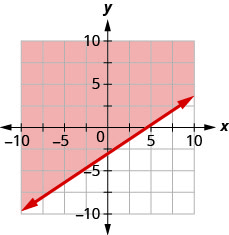
91. Escribe la desigualdad que muestra la gráfica con la línea límite$y=\frac{2}{3}x−3$.

$Esta figura tiene la gráfica de una línea recta en el plano de la coordenada x y. Los ejes x e y van de negativo 10 a 10. Se dibuja una línea a través de los puntos (0, negativo 3), (3, negativo 1) y (6, 1). La línea divide el plano de la coordenada x y en dos mitades. La línea y la mitad superior izquierda están sombreadas en rojo para indicar que aquí es donde están las soluciones de la desigualdad.$

Contestar: $y>\frac{2}{3}x−3$

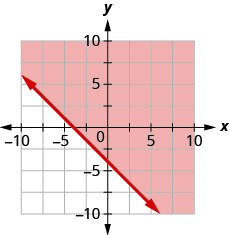
92. Escribe la desigualdad que muestra la región sombreada en la gráfica con la línea límite$x+y=−4$.

$Esta figura tiene la gráfica de una línea recta en el plano de la coordenada x y. Los ejes x e y van de negativo 10 a 10. Se dibuja una línea a través de los puntos (0, negativo 4), (negativo 2, negativo 2) y (negativo 4, 0). La línea divide el plano de la coordenada x y en dos mitades. La línea y la mitad superior derecha están sombreadas en rojo para indicar que aquí es donde están las soluciones de la desigualdad.$

93. Escribe la desigualdad que muestra la región sombreada en la gráfica con la línea límite$x−2y=6$.

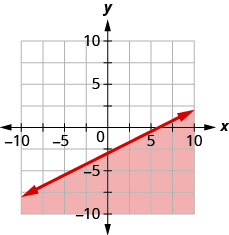
$Esta figura tiene la gráfica de una línea recta en el plano de la coordenada x y. Los ejes x e y van de negativo 10 a 10. Se dibuja una línea a través de los puntos (0, negativo 3), (2, negativo 2) y (6, 0). La línea divide el plano de la coordenada x y en dos mitades. La línea y la mitad inferior derecha están sombreadas en rojo para indicar que aquí es donde están las soluciones de la desigualdad.$

Contestar: $x−2y\geq 6$

Graficar desigualdades lineales en dos variables

En los siguientes ejercicios, grafica cada desigualdad lineal.

94. Grafica la desigualdad lineal$y>\frac{2}{5}x−4$.

95. Grafica la desigualdad lineal$y\leq −\frac{1}{4}x+3$.

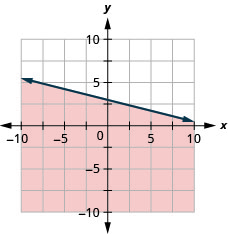
Contestar: $Esta figura tiene la gráfica de una línea discontinua recta en el plano de la coordenada x y. Los ejes x e y van de negativo 10 a 10. Se dibuja una línea discontinua recta a través de los puntos (0, 3), (4, 2) y (8, 1). La línea divide el plano de la coordenada x y en dos mitades. La mitad inferior izquierda está sombreada en rojo para indicar que aquí es donde están las soluciones de la desigualdad.$

96. Grafica la desigualdad lineal$x−y\leq 5$.

97. Graficar la desigualdad lineal$3x+2y>10.$

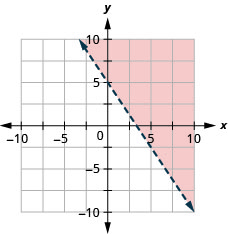
Contestar: $Esta figura tiene la gráfica de una línea discontinua recta en el plano de la coordenada x y. Los ejes x e y van de negativo 10 a 10. Se dibuja una línea discontinua recta a través de los puntos (0, 5), (2, 2) y (4, negativo 1). La línea divide el plano de la coordenada x y en dos mitades. La mitad superior derecha está sombreada en rojo para indicar que aquí es donde están las soluciones de la desigualdad.$

98. Grafica la desigualdad lineal$y\leq −3x$.

99. Graficar la desigualdad lineal$y<6.$

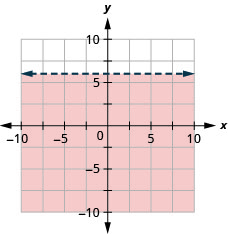
Contestar: $Esta figura tiene la gráfica de una línea discontinua horizontal recta en el plano de la coordenada x y. Los ejes x e y van de negativo 10 a 10. Se dibuja una línea discontinua recta a través de los puntos (0, 6), (1, 6) y (2, 6). La línea divide el plano de la coordenada x y en dos mitades. La mitad inferior está sombreada en rojo para indicar que aquí es donde están las soluciones de la desigualdad.$

Resolver aplicaciones usando desigualdades lineales en dos variables

100. Shanthie necesita ganar al menos $500 a la semana durante sus vacaciones de verano para pagar la universidad. Ella trabaja en dos trabajos. Uno como instructor de natación que paga $10 la hora y el otro como pasante en una oficina legal por $25 hora. ¿Cuántas horas necesita Shanthie para trabajar en cada trabajo para ganar al menos $500 por semana?

ⓐ Que x sea el número de horas que trabaja enseñando natación y que sea el número de horas que trabaja como pasante. Escribir una desigualdad que modelaría esta situación.
ⓑ Graficar la desigualdad.
ⓒ Encuentra tres pares ordenados$(x,y)$ que serían soluciones a la desigualdad. Entonces, explica lo que eso significa para Shanthie.

101. Atsushi necesita hacer ejercicio lo suficiente para quemar$600$ calorías cada día. Prefiere correr o andar en bicicleta y quema$20$ calorías por minuto mientras corre y$15$ calorías por minuto mientras anda en bicicleta.

ⓐ Si x es el número de minutos que corre Atsushi e y es el número de minutos que monta en bicicleta, encuentra la desigualdad que modela la situación.
ⓑ Graficar la desigualdad.
ⓒ Enumerar tres soluciones a la desigualdad. ¿Qué opciones ofrecen las soluciones Atsushi?

Contestar

ⓐ$20x+15y\geq 60020x+15y\geq 600$
ⓑ

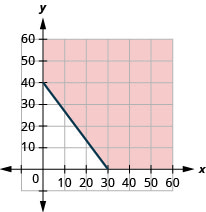
$La figura tiene una línea recta graficada en el plano de la coordenada x y. El eje x va de 0 a 50. El eje y va de 0 a 50. La línea pasa por los puntos (0, 40) y (30, 0). La línea divide el plano de coordenadas en dos mitades. La mitad superior derecha y la línea son de color rojo para indicar que este es el conjunto de soluciones.$

Relaciones y Funciones

Encontrar el dominio y el rango de una relación

En los siguientes ejercicios, para cada relación, ⓐ encuentra el dominio de la relación ⓑ encuentra el rango de la relación.

102. ${\{(5,−2),\,(5,−4),\,(7,−6),\,(8,−8),\,(9,−10)}\}$

103. ${\{(−3,7),\,(−2,3),\,(−1,9), \,(0,−3),\,(−1,8)}\}$

Contestar: ⓐ$D: {−3, −2, −1, 0}$
ⓑ$R: {7, 3, 9, −3, 8}$

En el siguiente ejercicio, utilice el mapeo de la relación a ⓐ lista los pares ordenados de la relación ⓑ encontrar el dominio de la relación ⓒ encontrar el rango de la relación.

104. El siguiente mapeo muestra el peso promedio de un niño según la edad.

$Esta figura muestra dos tablas que cada una tiene una columna. La tabla de la izquierda tiene el encabezado “Edad (años)” y enumera los números 1, 2, 3, 4, 5, 6 y 7. La tabla de la derecha tiene el encabezado “Peso (libras)” y enumera los números 20, 35, 30, 45, 40, 25 y 50. Hay flechas que comienzan en números en la tabla de edades y apuntando hacia los números en la tabla de pesos. La primera flecha va del 1 al 20. La segunda flecha va de 2 a 25. La tercera flecha va de 3 a 30. La cuarta flecha va de 4 a 35. La quinta flecha va de 5 a 40. La sexta flecha va del 6 al 45. La séptima flecha va del 7 al 50.$

En el siguiente ejercicio, usa la gráfica de la relación con ⓐ lista los pares ordenados de la relación ⓑ encuentra el dominio de la relación ⓒ encuentra el rango de la relación.

105.
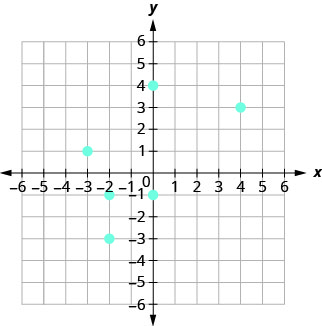
$La figura muestra la gráfica de algunos puntos en el plano de la coordenada x y. Los ejes x e y van de 6 a 6 negativos. Los puntos (negativo 3, 1), (negativo 2, negativo 1), (negativo 2, negativo 3), (0, negativo 1), (0, 4) y (4, 3).$

Contestar: ⓐ$(4, 3), \,(−2, −3), \,(−2, −1), \,(−3, 1), \,(0, −1), \,(0, 4)$
ⓑ$D: {−3, −2, 0, 4}$
ⓒ$R: {−3, −1, 1, 3, 4}$

Determinar si una relación es una función

En los siguientes ejercicios, utilice el conjunto de pares ordenados para ⓐ determinar si la relación es una función ⓑ encontrar el dominio de la relación ⓒ encontrar el rango de la relación.

106. ${\{(9,−5),\,(4,−3),\,(1,−1),\,(0,0),\,(1,1),\,(4,3),\,(9,5)}\}$

107. ${\{(−3,27),\,(−2,8),\,(−1,1),\,(0,0),\,(1,1),\,(2,8),\,(3,27)}\}$

Contestar: ⓐ si ⓑ${−3, −2, −1, 0, 1, 2, 3}$
ⓒ${0, 1, 8, 27}$

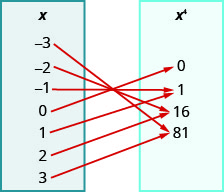
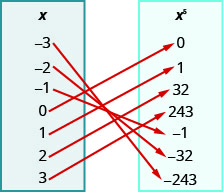
En los siguientes ejercicios, utilice el mapeo para ⓐ determinar si la relación es una función ⓑ encontrar el dominio de la función ⓒ encontrar el rango de la función.

108.
$Esta figura muestra dos tablas que cada una tiene una columna. La tabla de la izquierda tiene el encabezado “x” y enumera los números negativos 3, negativos 2, negativos 1, 0, 1, 2 y 3. La tabla de la derecha tiene la cabecera “x a la cuarta potencia” y enumera los números 0, 1, 16 y 81. Hay flechas que comienzan en números en la tabla x y apuntando hacia los números en la x a la cuarta tabla de poder. La primera flecha va del 3 negativo al 81. La segunda flecha va del 2 negativo al 16. La tercera flecha va de negativo 1 a 1. La cuarta flecha va de 0 a 0. La quinta flecha va de 1 a 1. La sexta flecha va del 2 al 16. La séptima flecha va del 3 al 81.$

109.
$Esta figura muestra dos tablas que cada una tiene una columna. La tabla de la izquierda tiene el encabezado “x” y enumera los números negativos 3, negativos 2, negativos 1, 0, 1, 2 y 3. La tabla de la derecha tiene la cabecera “x a la quinta potencia” y enumera los números 0, 1, 32, 243, negativo 1, negativo 32 y negativo 243. Hay flechas que comienzan en números en la tabla x y apuntando hacia los números en la x a la quinta tabla de poder. La primera flecha va de negativo 3 a negativo 243. La segunda flecha va de negativo 2 a negativo 32. La tercera flecha va de negativo 1 a 1. La cuarta flecha va de 0 a 0. La quinta flecha va de 1 a 1. La sexta flecha va de 2 a 32. La séptima flecha va de 3 a 243.$

Contestar: ⓐ${−3, −2, −1, 0, 1, 2, 3}$
ⓑ${−3, −2, −1, 0, 1, 2, 3}$
ⓒ${−243, −32, −1, 0, 1, 32, 243}$

En los siguientes ejercicios, determine si cada ecuación es una función.

110. $2x+y=−3$

111. $y=x^2$

Contestar: si

112. $y=3x−5$

113. $y=x^3$

Contestar: si

114. $2x+y2=4$

Encontrar el valor de una función

En los siguientes ejercicios, evalúe la función:

ⓐ$f(−2)$ ⓑ$f(3)$ ⓒ$f(a)$.

115. $f(x)=3x−4$

Contestar: ⓐ$f(−2)=−10$ ⓑ$f(3)=5$ ⓒ$f(a)=3a−4$

116. $f(x)=−2x+5$

117. $f(x)=x^2−5x+6$

Contestar: ⓐ$f(−2)=20$ ⓑ$f(3)=0$ ⓒ$f(a)=a^2−5a+6$

118. $f(x)=3x^2−2x+1$

En los siguientes ejercicios, evaluar la función.

119. $g(x)=3x2−5x;\space g(2)$

Contestar: $2$

120. $F(x)=2x2−3x+1;\space F(−1)$

121. $h(t)=4|t−1|+2;\space h(t)=4$

Contestar: $18$

122. $f(x)=x+2x−1;\space f(3)$

Gráficas de Funciones

Utilice la prueba de línea vertical

En los siguientes ejercicios, determine si cada gráfica es la gráfica de una función.

123.
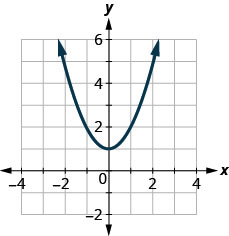
$La figura tiene una función cuadrada graficada en el plano de coordenadas x y. El eje x va desde el 6 negativo hasta el 6. El eje y va de 2 a 10 negativos. La parábola pasa por los puntos (negativo 2, 5), (negativo 1, 2), (0, 1), (1, 2) y (2, 5). El punto más bajo de la gráfica es (0, 1).$

Contestar: si

124.
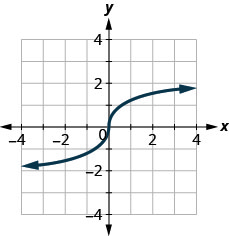
$La figura tiene una función en forma de s graficada en el plano de coordenadas x y. El eje x va desde el 6 negativo hasta el 6. El eje y va de 6 a 6 negativos. La curva pasa por los puntos (negativo 1, negativo 1), (0, 0) y (1, 1).$

125.
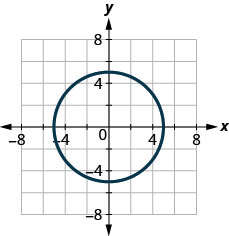
$La figura tiene un círculo graficado en el plano de la coordenada x y. El eje x va desde el 6 negativo hasta el 6. El eje y va de 6 a 6 negativos. El círculo pasa por los puntos (negativo 5, 0), (5, 0), (0, negativo 5) y (0, 5).$

Contestar: no

126.
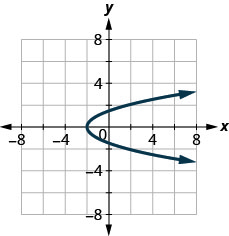
$La figura tiene una abertura de parábola a la derecha graficada en el plano de la coordenada x y. El eje x va desde el 6 negativo hasta el 6. El eje y va de 2 a 10 negativos. La parábola pasa por los puntos (negativo 2, 0), (negativo 1, 1), (negativo 1, negativo 1), (2, 2) y (2, negativo 2). El punto más a la izquierda en la gráfica es (negativo 2, 0).$

127.
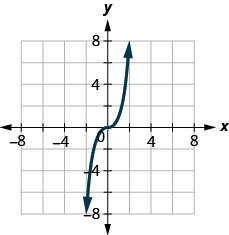
$La figura tiene una función de cubo graficada en el plano de coordenadas x y. El eje x va desde el 6 negativo hasta el 6. El eje y va de 6 a 6 negativos. La línea curva pasa por los puntos (negativo 1, negativo 1), (0, 0) y (1, 1).$

Contestar: si

128.
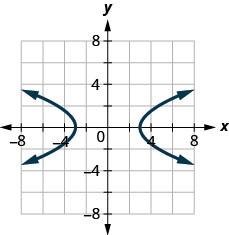
$La figura tiene dos líneas curvas graficadas en el plano de la coordenada x y. El eje x va desde el 6 negativo hasta el 6. El eje y va de 6 a 6 negativos. La línea curva de la izquierda pasa por los puntos (negativo 3, 0), (negativo 4, 2) y (negativo 4, negativo 2). La línea curva de la derecha pasa por los puntos (3, 0), (4, 2) y (4, negativo 2).$

129.
$La figura tiene una función de valor absoluto lateral graficada en el plano de coordenadas x y. El eje x va desde el 6 negativo hasta el 6. El eje y va de 6 a 6 negativos. La línea se dobla en el punto (0, negativo 1) y va hacia la derecha. La línea pasa por los puntos (1, 0), (1, negativo 2), (2, 1) y (2, negativo 3).$

Contestar: no

Identificar gráficas de funciones básicas

En los siguientes ejercicios, ⓐ grafica cada función ⓑ indica su dominio y rango. Escribe el dominio y el rango en notación de intervalos.

130. $f(x)=5x+1$

131. $f(x)=−4x−2$

Contestar

ⓐ

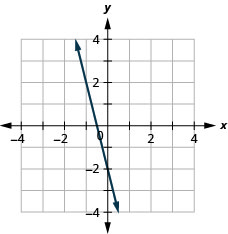
$La figura tiene una función lineal graficada en el plano de coordenadas x y. El eje x va desde el 6 negativo hasta el 6. El eje y va de 6 a 6 negativos. La línea pasa por los puntos (negativo 2, 6), (negativo 1, 2) y (0, negativo 2).$

ⓑ$D: (-\inf ,\inf ), R: (-\inf ,\inf )$

132. $f(x)=\frac{2}{3}x−1$

133. $f(x)=−6$

Contestar

ⓐ

$La figura tiene una función constante graficada en el plano de coordenadas x y. El eje x va desde el 6 negativo hasta el 6. El eje y va de negativo 8 a 4. La línea pasa por los puntos (0, negativo 6), (1, negativo 6) y (2, negativo 6).$

ⓑ$D: (-\inf ,\inf ), R: (-\inf ,\inf )$

134. $f(x)=2x$

135. $f(x)=3x^2$

Contestar

ⓐ

$La figura tiene una función cuadrada graficada en el plano de coordenadas x y. El eje x va desde el 6 negativo hasta el 6. El eje y va de 2 a 10 negativos. La parábola pasa por los puntos (negativos 1, 3), (0, 0) y (1, 3). El punto más bajo de la gráfica es (0, 0).$

ⓑ$D: (-\inf ,\inf ), R: (-\inf ,0]$

136. $f(x)=−12x^2$

137. $f(x)=x^2+2$

Contestar

ⓐ

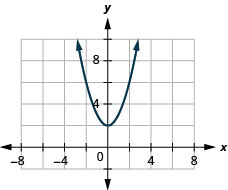
$La figura tiene una función cuadrada graficada en el plano de coordenadas x y. El eje x va desde el 6 negativo hasta el 6. El eje y va de negativo 4 a 8. La parábola pasa por los puntos (negativo 2, 6), (negativo 1, 3), (0, 2), (1, 3) y (2, 6). El punto más bajo de la gráfica es (0, 2).$

ⓑ$D: (-\inf ,\inf ), R: (-\inf ,\inf )$

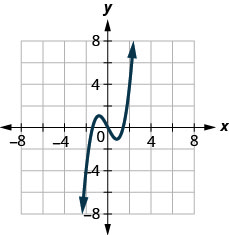
138. $f(x)=x^3−2$

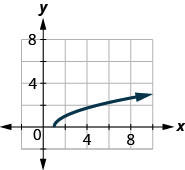
139. $f(x)=\sqrt{x+2}$

Contestar

ⓐ

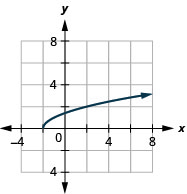
$La figura tiene una función de raíz cuadrada graficada en el plano de coordenadas x y. El eje x va de negativo 4 a 8. El eje y va de 2 a 10 negativos. La media línea comienza en el punto (negativo 2, 0) y pasa por los puntos (negativo 1, 1) y (2, 2).$

ⓑ$D: [−2,−2, \inf ), \space R: [0,\inf )$

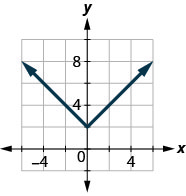
140. $f(x)=−|x|$

141. $f(x)=|x|+1$

Contestar

ⓐ

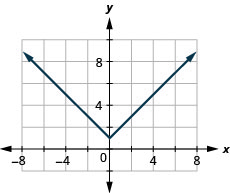
$La figura tiene una función de valor absoluto graficada en el plano de coordenadas x y. El eje x va desde el 6 negativo hasta el 6. El eje y va de 2 a 10 negativos. El vértice está en el punto (0, 1). La línea pasa por los puntos (negativo 1, 2) y (1, 2).$

ⓑ$D: (-\inf ,\inf ), \space R: [1,\inf )$

Leer información de una gráfica de una función

En los siguientes ejercicios, usa la gráfica de la función para encontrar su dominio y rango. Escribir el dominio y el rango en notación de intervalos

142.
$La figura tiene una función de raíz cuadrada graficada en el plano de coordenadas x y. El eje x va de 0 a 10. El eje y va de 0 a 10. La media línea inicia en el punto (1, 0) y pasa por los puntos (2, 1) y (5, 2).$

143.
$La figura tiene una función de valor absoluto graficada en el plano de coordenadas x y. El eje x va desde el 6 negativo hasta el 6. El eje y va de 2 a 10 negativos. El vértice está en el punto (0, 2). La línea pasa por los puntos (negativo 1, 3) y (1, 3).$

Contestar: $D: (-\inf ,\inf ), R: [2,\inf )$

144.
$La figura tiene una función cúbica graficada en el plano de coordenadas x y. El eje x va desde el 6 negativo hasta el 6. El eje y va de 6 a 6 negativos. La línea curva pasa por los puntos (negativo 2, negativo 4), (0, 0) y (2, 4).$

En los siguientes ejercicios, utilice la gráfica de la función para encontrar los valores indicados.

145.
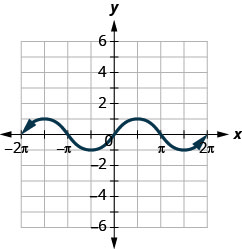
$Esta figura tiene una línea curva ondulada graficada en el plano de la coordenada x y. El eje x va de negativo 2 veces pi a 2 veces pi. El eje y va de 6 a 6 negativos. El segmento de línea curva pasa por los puntos (negativo 2 veces pi, 0), (negativo 3 dividido por 2 veces pi, 1), (negativo pi, 0), (negativo 1 dividido por 2 veces pi, negativo 1), (0, 0), (1 dividido por 2 veces pi, 1), (pi, 0), (3 dividido por 2 veces pi, negativo 1), y (2 veces pi, 0). Los puntos (negativo 3 dividido por 2 veces pi, 1) y (1 dividido por 2 veces pi, 1) son los puntos más altos de la gráfica. Los puntos (negativo 1 dividido por 2 veces pi, negativo 1) y (3 dividido por 2 veces pi, negativo 1) son los puntos más bajos de la gráfica. El patrón se extiende infinitamente hacia la izquierda y hacia la derecha.$

ⓐ Encontrar$f(0)$.
ⓑ Encontrar$f(12\pi )$.
ⓒ Encontrar$f(−32\pi )$.
ⓓ Encuentra los valores para$x$ cuándo$f(x)=0$.
ⓔ Encuentra las$x$ -intercepciones.
ⓕ Encuentra la (s)$y$ intercepción (s).
ⓖ Encuentra el dominio. Escríbelo en notación de intervalos.
ⓗ Encuentra la gama. Escríbelo en notación de intervalos.

Contestar: ⓐ$f(x)=0$ ⓑ$f(\pi /2)=1$
ⓒ$f(−3\pi /2)=1$ ⓓ$f(x)=0$ para$x=−2\pi ,−\pi ,0,\pi ,2\pi$
ⓔ$(−2\pi ,0), (−\pi ,0), (0,0), (\pi ,0), (2\pi ,0)$ ⓕ$(0,0)$
ⓖ$[−2\pi ,2\pi ]$ ⓗ$[−1,1]$

146.
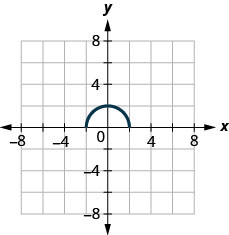
$La figura tiene un semicírculo graficado en el plano de la coordenada x y. El eje x va desde el 6 negativo hasta el 6. El eje y va de 6 a 6 negativos. El segmento de línea curva comienza en el punto (negativo 2, 0). La línea pasa por el punto (0, 2) y termina en el punto (2, 0). El punto (0, 2) es el punto más alto de la gráfica.$

ⓐ Encontrar$f(0)$.
ⓑ Encuentra los valores para$x$ cuándo$f(x)=0$.
ⓒ Encuentra las$x$ -intercepciones.
ⓓ Encuentra la (s)$y$ intercepción (s).
ⓔ Encuentra el dominio. Escríbelo en notación de intervalos.
ⓕ Encuentra la gama. Escríbelo en notación de intervalos.

Prueba de práctica

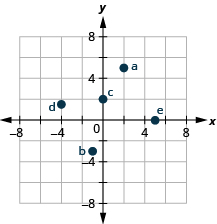
1. Trazar cada punto en un sistema de coordenadas rectangulares.

Contestar: $Esta figura muestra los puntos trazados en el plano de la coordenada x y. Los ejes x e y van de negativo 10 a 10. El punto etiquetado a está 2 unidades a la derecha del origen y 5 unidades por encima del origen y se ubica en el cuadrante I. El punto etiquetado b es 1 unidad a la izquierda del origen y 3 unidades por debajo del origen y se ubica en el cuadrante III. El punto etiquetado c está 2 unidades por encima del origen y se ubica en el eje y. El punto etiquetado con d está 4 unidades a la izquierda del origen y 1.5 unidades por encima del origen y se ubica en el cuadrante II. El punto etiquetado e está a 5 unidades a la derecha del origen y se ubica en el eje x.$

2. ¿Cuáles de los pares ordenados dados son soluciones a la ecuación$3x−y=6$?

3. Encuentra la pendiente de cada línea que se muestra.

ⓐ

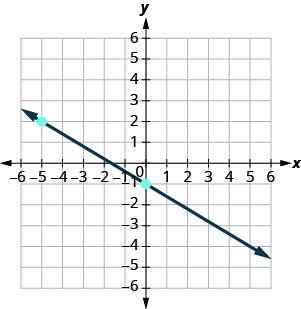
$La figura tiene una línea recta graficada en el plano de la coordenada x y. El eje x va de negativo 10 a 10. El eje y va de negativo 10 a 10. La línea pasa por los puntos (negativo 5, 2) (0, negativo 1), y (5, negativo 4).$

ⓑ

$La figura tiene una línea vertical recta graficada en el plano de la coordenada x y. El eje x va de negativo 10 a 10. El eje y va de negativo 10 a 10. La línea pasa por los puntos (2, 0) (2, negativo 1), y (2, 1).$

Contestar: ⓐ$−\frac{3}{5}$ ⓑ indefinido

4. Encuentra la pendiente de la línea entre los puntos$(5,2)$ y$(−1,−4)$.

5. Grafica la línea con pendiente$\frac{1}{2}$ que contiene el punto$(−3,−4)$.

Contestar: $La figura tiene una línea recta graficada en el plano de la coordenada x y. El eje x va de negativo 10 a 10. El eje y va de negativo 10 a 10. La línea pasa por los puntos (negativo 3, negativo 4) (negativo 1, negativo 3), y (1, negativo 2).$

6. Encuentra las intercepciones de$4x+2y=−8$ y grafica.

Grafica la línea para cada una de las siguientes ecuaciones.

7. $y=\frac{5}{3}x−1$

Contestar: $La figura tiene una línea recta graficada en el plano de la coordenada x y. El eje x va de negativo 10 a 10. El eje y va de negativo 10 a 10. La línea pasa por los puntos (negativo 3, negativo 6) (0, negativo 1), y (3, 4).$

8. $y=−x$

9. $y=2$

Contestar: $La figura tiene una línea horizontal recta graficada en el plano de la coordenada x y. El eje x va de negativo 10 a 10. El eje y va de negativo 10 a 10. La línea pasa por los puntos (negativo 1, 2) (0, 2), y (1, 2).$

Encuentra la ecuación de cada línea. Escribe la ecuación en forma de pendiente-intercepción.

10. pendiente$−\frac{3}{4}$ e$y$ -intercepción$(0,−2)$

11. $m=2$, punto$(−3,−1)$

Contestar: $y=2x+5$

12. que contenga$(10,1)$ y$(6,−1)$

13. perpendicular a la línea$y=\frac{5}{4}x+2$, que contiene el punto$(−10,3)$

Contestar: $y=−\frac{4}{5}x−5$

14. Escribe la desigualdad que muestra la gráfica con la línea límite$y=−x−3$.

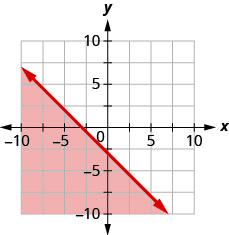
$La figura tiene una línea recta graficada en el plano de la coordenada x y. El eje x va de negativo 10 a 10. El eje y va de negativo 10 a 10. La línea pasa por los puntos (negativo 3, 0), (0, negativo 3) y (1, negativo 4). La línea divide el plano de coordenadas en dos mitades. La mitad inferior izquierda y la línea son de color rojo para indicar que este es el conjunto de soluciones.$

Grafica cada desigualdad lineal.

15. $y>\frac{3}{2}x+5$

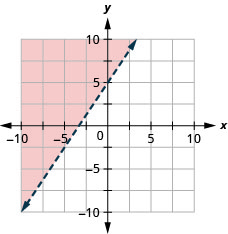
Contestar: $La figura tiene una línea discontinua recta graficada en el plano de coordenadas x y. El eje x va de negativo 10 a 10. El eje y va de negativo 10 a 10. La línea pasa por los puntos (negativo 2, 2), (0, 5) y (2, 8). La línea divide el plano de coordenadas en dos mitades. La mitad superior izquierda es de color rojo para indicar que este es el conjunto de soluciones.$

16. $x−y\geq −4$

17. $y\leq −5x$

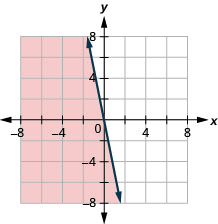
Contestar: $La figura tiene una línea recta graficada en el plano de la coordenada x y. El eje x va de negativo 8 a 8. El eje y va de negativo 8 a 8. La línea pasa por los puntos (negativo 1, 5), (0, 0) y (1, negativo 5). La línea divide el plano de coordenadas en dos mitades. La mitad inferior izquierda y la línea son de color rojo para indicar que este es el conjunto de soluciones.$

18. Hiro trabaja dos trabajos a tiempo parcial con el fin de ganar suficiente dinero para cumplir con sus obligaciones de al menos 450 dólares a la semana. Su trabajo en el centro comercial paga $10 la hora y su trabajo de auxiliar administrativo en el campus paga $15 la hora. ¿Cuántas horas necesita Hiro para trabajar en cada trabajo para ganar al menos 450 dólares?

ⓐ Deja x ser el número de horas que trabaja en el centro comercial y deja y ser el número de horas que trabaja como auxiliar administrativa. Escribir una desigualdad que modelaría esta situación.
ⓑ Graficar la desigualdad.
ⓒ Encuentra tres pares ordenados$(x,y)$ que serían soluciones a la desigualdad. Entonces explica lo que eso significa para Hiro.

19. Utilice el conjunto de pares ordenados para ⓐ determinar si la relación es una función, ⓑ encontrar el dominio de la relación y ⓒ encontrar el rango de la relación.

\ ({\ {(−3,27), (−2,8), (−1,1), (0,0),
(1,1), (2,8), (3,27)}\}\)

$f(x)=4x^2−2x−3$

21. Para$h(y)=3|y−1|−3$, evaluar$h(−4)$.

Contestar: $12$

22. Determinar si la gráfica es la gráfica de una función. Explique su respuesta.

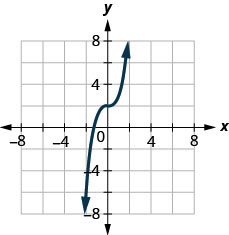
$La figura tiene una función de cubo graficada en el plano de coordenadas x y. El eje x va desde el 6 negativo hasta el 6. El eje y va de 6 a 6 negativos. La línea curva pasa por los puntos (negativos 1, 1), (0, 2) y (1, 3).$

En los siguientes ejercicios, ⓐ grafica cada función ⓑ indica su dominio y rango.
Escribe el dominio y el rango en notación de intervalos.

23. $f(x)=x^2+1$

Contestar

ⓐ

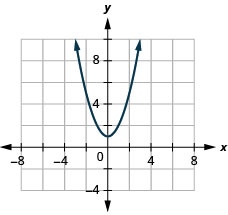
$La figura tiene una función cuadrada graficada en el plano de coordenadas x y. El eje x va desde el 6 negativo hasta el 6. El eje y va de 2 a 10 negativos. La parábola pasa por los puntos (negativo 2, 5), (negativo 1, 2), (0, 1), (1, 2) y (2, 5). El punto más bajo de la gráfica es (0, 1).$

ⓑ$D: (-\inf ,\inf ), R: [1,\inf )$

24. $f(x)=\sqrt{x+1}$

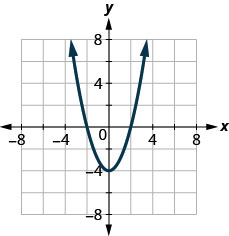
$La figura tiene una función cuadrada graficada en el plano de coordenadas x y. El eje x va desde el 6 negativo hasta el 6. El eje y va de 6 a 6 negativos. La parábola pasa por los puntos (negativo 2, 0), (negativo 1, negativo 3), (0, negativo 4), (1, negativo 3) y (2, 0). El punto más bajo en la gráfica es (0, negativo 4).$

ⓑ Encuentra las$y$ -intercepciones.
ⓒ Encontrar$f(−1)$.
ⓓ Encontrar$f(1)$.
ⓔ Encuentra el dominio. Escríbelo en notación de intervalos.
ⓕ Encuentra la gama. Escríbelo en notación de intervalos.