Capítulo 4 Ejercicios de revisión
- Page ID
- 112348
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Ejercicios de revisión de capítulos
Resolver Sistemas de Ecuaciones Lineales con Dos Variables
Determinar si un Par Ordenado es una Solución de un Sistema de Ecuaciones.
En los siguientes ejercicios, determinar si los siguientes puntos son soluciones al sistema de ecuaciones dado.
1. \(\left\{ \begin{array} {l} x+3y=−9\\2x−4y=12 \end{array} \right.\)
ⓐ\((−3,−2)\)
ⓑ\((0,−3)\)
2. \(\left\{ \begin{array} {l} x+y=8\\y=x−4 \end{array} \right.\)
ⓐ\((6,2)\)
ⓑ\((9,−1)\)
- Contestar
-
ⓐ si ⓑ no
Resolver un sistema de ecuaciones lineales mediante gráficos
En los siguientes ejercicios, resuelve los siguientes sistemas de ecuaciones mediante la gráfica.
3. \(\left\{ \begin{array} {l} 3x+y=6\\x+3y=−6 \end{array} \right.\)
4. \(\left\{ \begin{array} {l} x+4y=−1\\x=3 \end{array} \right.\)
- Contestar
-
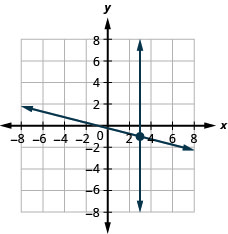
\((3,−1)\)
5. \(\left\{ \begin{array} {l} 2x−y=5\\4x−2y=10 \end{array} \right.\)
6. \(\left\{ \begin{array} {l} −x+2y=4\\y=\frac{1}{2}x−3 \end{array} \right.\)
- Contestar
-
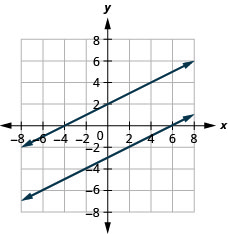
no hay solución
En los siguientes ejercicios, sin graficar determinar el número de soluciones y luego clasificar el sistema de ecuaciones.
7. \(\left\{ \begin{array} {l} y=\frac{2}{5}x+2\\−2x+5y=10 \end{array} \right.\)
8. \(\left\{ \begin{array} {l} 3x+2y=6\\y=−3x+4 \end{array} \right.\)
- Contestar
-
una solución, sistema consistente, ecuaciones independientes
9. \(\left\{ \begin{array} {l} 5x−4y=0\\y=\frac{5}{4}x−5 \end{array} \right.\)
Resolver un sistema de ecuaciones por sustitución
En los siguientes ejercicios, resolver los sistemas de ecuaciones por sustitución.
10. \(\left\{ \begin{array} {l} 3x−2y=2\\y=\frac{1}{2}x+3 \end{array} \right.\)
- Contestar
-
\((4,5)\)
11. \(\left\{ \begin{array} {l} x−y=0\\2x+5y=−14 \end{array} \right.\)
12. \(\left\{ \begin{array} {l} y=−2x+7\\y=\frac{2}{3}x−1 \end{array} \right.\)
- Contestar
-
\((3,1)\)
13. \(\left\{ \begin{array} {l} y=−5x\\5x+y=6 \end{array} \right.\)
14. \(\left\{ \begin{array} {l} y=−\frac{1}{3}x+2\\x+3y=6 \end{array} \right.\)
- Contestar
-
infinitamente muchas soluciones
Resolver un sistema de ecuaciones por eliminación
En los siguientes ejercicios, resolver los sistemas de ecuaciones por eliminación
15. \(\left\{ \begin{array} {l} x+y=12\\x−y=−10 \end{array} \right.\)
16. \(\left\{ \begin{array} {l} 3x−8y=20\\x+3y=1 \end{array} \right.\)
- Contestar
-
\((4,−1)\)
17. \(\left\{ \begin{array} {l} 9x+4y=2\\5x+3y=5 \end{array} \right.\)
18. \(\left\{ \begin{array} {l} \frac{1}{3}x−\frac{1}{2}y=1\\ \frac{3}{4}x−y=\frac{5}{2} \end{array} \right.\)
- Contestar
-
\((6,2)\)
19. \(\left\{ \begin{array} {l} −x+3y=8\\2x−6y=−20 \end{array} \right.\)
Elija el método más conveniente para resolver un sistema de ecuaciones lineales
En los siguientes ejercicios, decidir si sería más conveniente resolver el sistema de ecuaciones por sustitución o eliminación.
20. \(\left\{ \begin{array} {l} 6x−5y=27\\3x+10y=−24 \end{array} \right.\)
- Contestar
-
eliminación
21. \(\left\{ \begin{array} {l} y=3x−9\\4x−5y=23 \end{array} \right.\)
Resolver aplicaciones con sistemas de ecuaciones
Resolver aplicaciones de traducción directa
En los siguientes ejercicios, traducir a un sistema de ecuaciones y resolver.
22. Mollie quiere plantar 200 bulbos en su jardín, todos los lirios y tulipanes. Ella quiere plantar tres veces más tulipanes que lirios. ¿Cuántos lirios y cuántos tulipanes debe plantar?
- Contestar
-
50 lirios y 150 tulipanes
23. Ashanti ha sido ofertada por dos compañías telefónicas. La primera empresa paga un salario de $22,000 más una comisión de $100 por cada contrato vendido. El segundo paga un salario de 28,000 dólares más una comisión de 25 dólares por cada contrato vendido. ¿Cuántos contratos necesitarían venderse para que el total pague igual?
24. Leroy pasó 20 minutos trotando y 40 minutos en bicicleta y quemó 600 calorías. Al día siguiente, Leroy intercambió tiempos, haciendo 40 minutos de trotar y 20 minutos de ciclismo y quemó la misma cantidad de calorías. ¿Cuántas calorías se quemaron por cada minuto de trotar y cuántas por cada minuto de ciclismo?
- Contestar
-
10 calorías para correr y 10 calorías en bicicleta
25. Troy y Lisa estaban comprando útiles escolares. Cada uno compró diferentes cantidades del mismo cuaderno y calculadora. Troy compró cuatro cuadernos y cinco calculadoras por 116 dólares. Lisa compró dos cuadernos y tres calculadoras por 68 dólares. Encuentre el costo de cada portátil y cada unidad de disco USB.
Resolver aplicaciones de geometría
En los siguientes ejercicios, traducir a un sistema de ecuaciones y resolver.
26. La diferencia de dos ángulos suplementarios es de 58 grados. Encuentra las medidas de los ángulos.
- Contestar
-
119, 61
27. Dos ángulos son complementarios. La medida del ángulo mayor es cinco más de cuatro veces la medida del ángulo más pequeño. Encuentra las medidas de ambos ángulos.
28. La medida de uno de los ángulos pequeños de un triángulo rectángulo es 15 menos del doble de la medida del otro ángulo pequeño. Encuentra la medida de ambos ángulos.
- Contestar
-
\(35°\)y\(55°\)
29. Becca está colgando una guirnalda floral de 28 pies en los dos lados y la parte superior de una pérgola para prepararse para una boda. La altura es cuatro pies menos que el ancho. Encuentra la altura y anchura de la pérgola.
30. El perímetro de un parque rectangular de la ciudad es de 1428 pies. La longitud es de 78 pies más del doble de ancho. Encuentra el largo y ancho del parque.
- Contestar
-
el largo es de 450 pies, el ancho es de 264 pies
Resolver aplicaciones de movimiento uniforme
En los siguientes ejercicios, traducir a un sistema de ecuaciones y resolver.
31. Sheila y Lenore conducían a la casa de su abuela. Lenore se fue una hora después de Sheila. Sheila condujo a una velocidad de 45 mph, y Lenore condujo a una velocidad de 60 mph. ¿Cuánto tiempo tardará Lenore en ponerse al día con Sheila?
32. Bob salió de casa, montando su bicicleta a razón de 10 millas por hora para ir al lago. Cheryl, su esposa, salió 45 minutos (34 (34 horas) después, conduciendo su automóvil a razón de 25 millas por hora. ¿Cuánto tiempo le tomará a Cheryl ponerse al día con Bob?
- Contestar
-
\(12\)una hora
33. Marcus puede conducir su bote 36 millas río abajo en tres horas pero tarda cuatro horas en regresar río arriba. Encuentra la tarifa de la embarcación en agua sin gas y la tasa de la corriente.
34. Un jet de pasajeros puede volar 804 millas en 2 horas con viento de cola pero solo 776 millas en 2 horas en viento en contra. Encuentra la velocidad del jet en aire quieto y la velocidad del viento.
- Contestar
-
la velocidad del jet es de 395 mph, la velocidad del viento es de 7 mph
Resolver aplicaciones de mezcla con sistemas de ecuaciones
Resolver aplicaciones de mezcla con sistemas de ecuaciones
Para los siguientes ejercicios, traduzca a un sistema de ecuaciones y resuelva.
35. Lynn pagó un total de $2,780 por 261 boletos para el teatro. Los boletos para estudiantes cuestan $10 y los boletos para adultos cuestan $15. ¿Cuántos boletos de estudiante y cuántos boletos de adulto compró Lynn?
36. Priam tiene centavos y centavos en un portavasos en su auto. El valor total de las monedas es de $4.21. El número de diez centavos es tres menos de cuatro veces el número de centavos. ¿Cuántas monedas de diez centavos y cuántos centavos hay en la copa?
- Contestar
-
41 centavos y 11 centavos
37. Yumi quiere hacer 12 tazas de mezcla de fiesta usando caramelos y nueces. Su presupuesto requiere que la mezcla de fiesta le cueste $1.29 por taza. Los caramelos son $2.49 por taza y los frutos secos son $0.69 por taza. ¿Cuántas tazas de caramelos y cuántas tazas de frutos secos debe usar?
38. Un científico necesita 70 litros de una solución al 40% de alcohol. Tiene una solución de 30% y 60% disponible. ¿Cuántos litros del 30% y cuántos litros de las soluciones al 60% debe mezclar para hacer la solución del 40%?
- Contestar
-
\(46\frac{2}{3}\)litros de solución al 30%,\(23\frac{1}{3}\) litros de solución al 60%
Resolver aplicaciones de interés
Para los siguientes ejercicios, traduzca a un sistema de ecuaciones y resuelva.
39. Jack tiene $12,000 para invertir y quiere ganar 7.5% de interés por año. Pondrá parte del dinero en una cuenta de ahorro que gana 4% anual y el resto en cuenta CD que gana 9% anual. ¿Cuánto dinero debe poner en cada cuenta?
40. Cuando se gradúe de la universidad, Linda deberá 43,000 dólares en préstamos estudiantiles. La tasa de interés de los préstamos federales es de 4.5% y la tasa de los préstamos bancarios privados es de 2%. El interés total que debe por un año fue de $1,585. ¿Cuál es el monto de cada préstamo?
- Contestar
-
$29,000 para el préstamo federal, $14,000 para el préstamo privado
Resolver Sistemas de Ecuaciones con Tres Variables
Resolver Sistemas de Ecuaciones con Tres Variables
En los siguientes ejercicios, determinar si el triple ordenado es una solución al sistema.
41. \(\left\{ \begin{array} {l} 3x−4y−3z=2\\2x−6y+z=3\\2x+3y−2z=3 \end{array} \right.\)
ⓐ\((2,3,−1)\)
ⓑ\((3,1,3)\)
42. \(\left\{ \begin{array} {l} y=\frac{2}{3}x−2\\x+3y−z=15\\x−3y+z=−2 \end{array} \right.\)
ⓐ\((−6,5,\frac{1}{2})\)
ⓑ\((5,\frac{4}{3},−3)\)
- Contestar
-
ⓐ no ⓑ si
Resolver un Sistema de Ecuaciones Lineales con Tres Variables
En los siguientes ejercicios, resolver el sistema de ecuaciones.
43. \(\left\{ \begin{array} {l} 3x−5y+4z=5\\5x+2y+z=0\\2x+3y−2z=3 \end{array} \right.\)
44. \(\left\{ \begin{array} {l} x+\frac{5}{2}y+z=−2\\2x+2y+\frac{1}{2}z=−4\\ \frac{1}{3}x−y−z=1 \end{array} \right.\)
- Contestar
-
\((−3,2,−4)\)
45. \(\left\{ \begin{array} {l} 5x+3y=−6\\2y+3z=−1\\7x+z=1 \end{array} \right.\)
46. \(\left\{ \begin{array} {l} 2x+3y+z=12\\x+y+z=9\\3x+4y+2z=20 \end{array} \right.\)
- Contestar
-
sin solución
47. \(\left\{ \begin{array} {l} −x−3y+2z=14\\−x+2y−3z=−4\\3x+y−2z=6 \end{array} \right.\)
Resolver aplicaciones usando sistemas de ecuaciones lineales con tres variables
48. Después de asistir a un partido de béisbol de Grandes Ligas, los mecenas suelen comprar recuerdos. Si una familia compra 4 playeras, una gorra y 1 peluche su total es de 135 dólares. Una pareja compra 2 playeras, una gorra y 3 peluches para sus sobrinas y gasta 115 dólares. Otra pareja compra 2 playeras, una gorra y 1 peluche y su total es de 85 dólares. ¿Cuál es el costo de cada artículo?
- Contestar
-
\(25, 20, 15\)
Resolver Sistemas de Ecuaciones Usando Matrices
Escribir la Matriz Aumentada para un Sistema de Ecuaciones.
Escribe cada sistema de ecuaciones lineales como una matriz aumentada.
49. \(\left\{ \begin{array} {l} 3x−y=−1\\−2x+2y=5 \end{array} \right.\)
50. \(\left\{ \begin{array} {l} 4x+3y=−2\\x−2y−3z=7\\2x−y+2z=−6 \end{array} \right.\)
- Contestar
-
\(\left[ \begin{matrix} 4&3&0&−2\\1&−2&−3&7\\2&−1&2&−6 \end{matrix} \right]\)
Escribir el sistema de ecuaciones que corresponda a la matriz aumentada.
51. \(\left[ \begin{array} {cc|c} 2&−4&-2\\3&−3&-1 \end{array} \right]\)
52. \(\left[ \begin{array} {ccc|c} 1&0&−3&-1\\1&−2&0&-2\\0&−1&2&3 \end{array} \right]\)
- Contestar
-
\(\left\{ \begin{array} {l} x−3z=−1\\x−2y=−27\\−y+2z=3 \end{array} \right.\)
En los siguientes ejercicios, realizar las operaciones indicadas sobre las matrices aumentadas.
53. \(\left[ \begin{array} {cc|c} 4&−6&-3\\3&2&1 \end{array} \right]\)
ⓐ Intercambias filas 2 y 1.
ⓑ Multiplica la fila 1 por 4.
ⓒ Multiplica la fila 2 por 3 y agrega a la fila 1.
54. \(\left[ \begin{array} {ccc|c} 1&−3&−2&4\\2&2&−1&-3\\4&−2&−3&-1 \end{array} \right]\)
ⓐ Intercambias filas 2 y 3.
ⓑ Multiplica la fila 1 por 2.
ⓒ Multiplica la fila 3 por −2−2 y agrega a la fila 2.
- Contestar
-
ⓐ\(\left[ \begin{matrix} 1&−3&−2&4\\4&−2&−3&−1\\2&2&−1&−3 \end{matrix} \right]\)
ⓑ\(\left[ \begin{matrix} 2&−6&−4&8\\4&−2&−3&−1\\2&2&−1&−3 \end{matrix} \right]\)
ⓒ\(\left[ \begin{matrix} 2&−6&−4&8\\4&−2&−3&−1\\0&−6&−1&5 \end{matrix} \right]\)
Resolver Sistemas de Ecuaciones Usando Matrices
En los siguientes ejercicios, resuelve cada sistema de ecuaciones utilizando una matriz.
55. \(\left\{ \begin{array} {l} 4x+y=6\\x−y=4 \end{array} \right.\)
56. \(\left\{ \begin{array} {l} 2x−y+3z=−3\\−x+2y−z=10\\x+y+z=5 \end{array} \right.\)
- Contestar
-
\((−2,5,−2)\)
57. \(\left\{ \begin{array} {l} 2y+3z=−1\\5x+3y=−6\\7x+z=1 \end{array} \right.\)
58. \(\left\{ \begin{array} {l} x+2y−3z=−1\\x−3y+z=1\\2x−y−2z=2 \end{array} \right.\)
- Contestar
-
sin solución
59. \(\left\{ \begin{array} {l} x+y−3z=−1\\y−z=0\\−x+2y=1 \end{array} \right.\)
Resolver Sistemas de Ecuaciones Usando Determinantes
Evaluar el Determinante de una Matriz de 2 × 2
En el siguiente ejercicio, evaluar el determinado de la matriz cuadrada.
60. \(\left[ \begin{matrix} 8&−4\\5&−3 \end{matrix} \right]\)
- Contestar
-
\(−4\)
Evaluar el Determinante de una Matriz de 3 × 3
En el siguiente ejercicio, encontrar y luego evaluar a los menores indicados.
61. \(\left| \begin{matrix} −1&−3&2\\4&−2&−1\\−2&0&−3 \end{matrix} \right|\); Encuentra al menor ⓐ\(a_1\) ⓑ\(b_1\) ⓒ\(c_2\)
En el siguiente ejercicio, evaluar cada determinante expandiendo por menores a lo largo de la primera fila.
62. \(\left| \begin{matrix} −2&−3&−4\\5&−6&7\\−1&2&0 \end{matrix} \right|\)
- Contestar
-
\(21\)En el siguiente ejercicio, evaluar cada determinante expandiendo por menores.
63. \(\left| \begin{matrix} 3&5&4\\−1&3&0\\−2&6&1 \end{matrix} \right|\)
Usa la Regla de Cramer para Resolver Sistemas de Ecuaciones
En los siguientes ejercicios, resuelve cada sistema de ecuaciones usando la regla de Cramer
64. \(\left\{ \begin{array} {l} x−3y=−9\\2x+5y=4 \end{array} \right.\)
- Contestar
-
\((−3,2)\)
65. \(\left\{ \begin{array} {l} 4x−3y+z=7\\2x−5y−4z=3\\3x−2y−2z=−7 \end{array} \right.\)
66. \(\left\{ \begin{array} {l} 2x+5y=4\\3y−z=3\\4x+3z=−3 \end{array} \right.\)
- Contestar
-
\((−3,2,3)\)
67. \(\left\{ \begin{array} {l} x+y−3z=−1\\y−z=0\\−x+2y=1 \end{array} \right.\)
68. \(\left\{ \begin{array} {l} 3x+4y−3z=−2\\2x+3y−z=−1\\2x+y−2z=6 \end{array} \right.\)
- Contestar
-
inconsistente
Resolver aplicaciones usando determinantes
En los siguientes ejercicios, determinar si los puntos dados son colineales.
69. \((0,2)\),\((−1,−1)\), y\((−2,4)\)
Graficando Sistemas de Desigualdades Lineales
Determinar si un par ordenado es una solución de un sistema de desigualdades lineales
En los siguientes ejercicios, determine si cada par ordenado es una solución al sistema.
70. \(\left\{ \begin{array} {l} 4x+y>6\\3x−y\leq 12 \end{array} \right.\)
ⓐ\((2,−1)\)
ⓑ\((3,−2)\)
- Contestar
-
ⓐ si ⓑ no
71. \(\left\{ \begin{array} {l} y>\frac{1}{3}x+2\\x−\frac{1}{4}y\leq 10 \end{array} \right.\)
ⓐ\((6,5)\)
ⓑ\((15,8)\)
Resolver un Sistema de Desigualdades Lineales Graficando
En los siguientes ejercicios, resuelve cada sistema graficando.
72. \(\left\{ \begin{array} {l} y<3x+1\\y\geq −x−2 \end{array} \right.\)
- Contestar
-
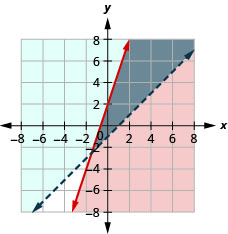
La solución es la región gris.
73. \(\left\{ \begin{array} {l} x−y>−1\\y<\frac{1}{3}x−2 \end{array} \right.\)
74. \(\left\{ \begin{array} {l} 2x−3y<6\\3x+4y\geq 12 \end{array} \right.\)
- Contestar
-
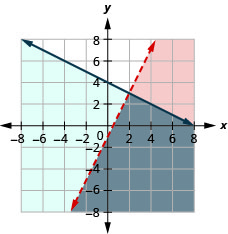
La solución es la región gris.
75. \(\left\{ \begin{array} {l} y\leq −\frac{3}{4}x+1\\x\geq −5 \end{array} \right.\)
76. \(\left\{ \begin{array} {l} x+3y<5\\y\geq -\frac{1}{3}x+6 \end{array} \right.\)
- Contestar
-
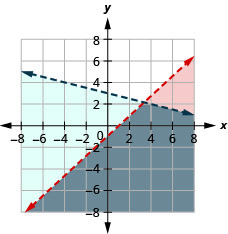
Sin solución.
77. \(\left\{ \begin{array} {l} y\geq 2x−5\\−6x+3y>−4 \end{array} \right.\)
Resolver Aplicaciones de Sistemas de Desigualdades
En los siguientes ejercicios, traducir a un sistema de desigualdades y resolver.
78. Roxana fabrica pulseras y collares y los vende en el mercado de agricultores. Ella vende las pulseras por $12 cada una y los collares por $18 cada una. En el mercado el próximo fin de semana tendrá espacio para exhibir no más de 40 piezas, y necesita vender por lo menos $500 para obtener ganancias.
ⓐ Escribir un sistema de desigualdades para modelar esta situación.
ⓑ Grafica el sistema.
ⓒ ¿Debería exhibir 26 pulseras y 14 collares?
ⓓ ¿Debería exhibir 39 pulseras y 1 collar?
- Contestar
-
ⓐ\(\left\{ \begin{array} {l} b\geq 0\\ n\geq 0\\ b+n\leq 40\\12b+18n\geq 500 \end{array} \right.\)
ⓑ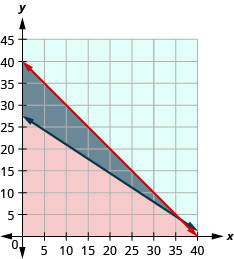
ⓒ si
ⓓ no
79. Annie tiene un presupuesto de 600 dólares para comprar libros de bolsillo y libros de tapa dura para su salón de clases. Ella quiere que el número de tapa dura sea al menos 5 más de tres veces el número de libros de bolsillo. Los libros de bolsillo cuestan $4 cada uno y los libros de tapa dura cuestan $15 cada uno
ⓐ Escribir un sistema de desigualdades para modelar esta situación.
ⓑ Grafica el sistema.
ⓒ ¿Puede comprar 8 libros de bolsillo y 40 libros de tapa dura?
ⓓ ¿Puede comprar 10 libros de bolsillo y 37 libros de tapa dura?
Prueba de práctica de capítulo
En los siguientes ejercicios, resuelve los siguientes sistemas graficando.
1. \(\left\{ \begin{array} {l} x−y=5\\x+2y=−4 \end{array} \right.\)
- Contestar
-
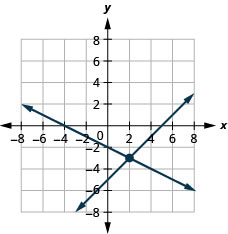
\((2,−3)\)
2. \(\left\{ \begin{array} {l} x−y>−2\\y\leq 3x+1 \end{array} \right.\)
En los siguientes ejercicios, resuelve cada sistema de ecuaciones. Use ya sea sustitución o eliminación.
3. \(\left\{ \begin{array} {l} x+4y=6\\−2x+y=−3 \end{array} \right.\)
- Contestar
-
\((2,1)\)
4. \(\left\{ \begin{array} {l} −3x+4y=2\\5x−5y=−23 \end{array} \right.\)
5. \(\left\{ \begin{array} {l} x+y−z=−1\\2x−y+2z=8\\−3x+2y+z=−9 \end{array} \right.\)
- Contestar
-
\((2,−2,1)\)
Resolver el sistema de ecuaciones usando una matriz.
6. \(\left\{ \begin{array} {l} 2x+y=7\\x−2y=6 \end{array} \right.\)
7. \(\left\{ \begin{array} {l} −3x+y+z=−4\\−x+2y−2z=1\\2x−y−z=−1 \end{array} \right.\)
- Contestar
-
\((5,7,4)\)
Resuelve usando la regla de Cramer.
8. \(\left\{ \begin{array} {l} 3x+y=−3\\2x+3y=6 \end{array} \right.\)
9. Evaluar el determinante expandiendo por menores:
\(\left| \begin{matrix} 3&−2&−2\\2&−1&4\\−1&0&−3 \end{matrix} \right|\)
- Contestar
-
\(99\)
En los siguientes ejercicios, traducir a un sistema de ecuaciones y resolver.
10. Greg está remando su canoa río arriba, contra la corriente, hasta un lugar de pesca a 10 millas de distancia. Si rema aguas arriba durante 2.5 horas y su viaje de regreso dura 1.25 horas, encuentra la velocidad de la corriente y su velocidad de remo en agua sin gas.
11. Un farmacéutico necesita 20 litros de una solución salina al 2%. Tiene una solución de 1% y 5% disponible. ¿Cuántos litros del 1% y cuántos litros de las soluciones al 5% debe mezclar para hacer la solución al 2%?
- Contestar
-
15 litros de solución al 1%, 5 litros de solución al 5%
12. Arnold invirtió 64 mil dólares, algunos con 5.5% de interés y el resto en 9%. ¿Cuánto invirtió a cada tasa si recibió 4.500 dólares en interés en un año?
13. El grupo de jóvenes de la iglesia está vendiendo bocadillos para recaudar dinero para asistir a su convención. Amy vendió 2 libras de dulces, 3 cajas de galletas y 1 lata de palomitas de maíz por un total de ventas de $65. Brian vendió 4 libras de dulces, 6 cajas de galletas y 3 latas de palomitas de maíz por un total de ventas de $140. Paulina vendió 8 libras de dulces, 8 cajas de galletas y 5 latas de palomitas de maíz por un total de ventas de $250. ¿Cuál es el costo de cada artículo?
- Contestar
-
El caramelo cuesta $20; las galletas cuestan $5; y las palomitas cuestan $10.
14. El fabricante de una barra de granola gasta $1.20 para hacer cada barra y las vende por $2. El fabricante también tiene costos fijos cada mes de $8,000.
ⓐ Encuentra la función de costo C cuando se fabrican x barras de granola
ⓑ Encuentra la función de ingresos R cuando se venden x barras de granola.
ⓒ Muestre el punto de equilibrio graficando las funciones Ingresos y Costo en la misma cuadrícula.
ⓓ Encuentra el punto de equilibrio. Interpreta lo que significa el punto de equilibrio.
15. Traducir a un sistema de desigualdades y resolver.
Andi quiere gastar no más de 50 dólares en golosinas de Halloween. Ella quiere comprar barras de caramelo que cuestan $1 cada una y piruletas que cuestan $0.50 cada una, y quiere que el número de piruletas sea al menos tres veces el número de barras de caramelo.
ⓐ Escribir un sistema de desigualdades para modelar esta situación.
ⓑ Grafica el sistema.
ⓒ ¿Puede comprar 20 barras de caramelo y 40 piruletas?
- Contestar
-
ⓐ\(\left\{ \begin{array} {l} C\geq 0\\ L\geq 0\\ C+0.5L\leq 50 \\ L\geq 3C \end{array} \right.\)
ⓑ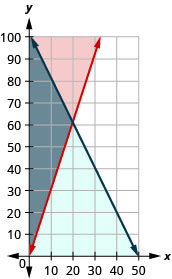
ⓒ no
ⓓ si


